![Performance Analysis
Aim of this course is to develop skills for making evaluative judgments
about algorithm.
There are two criteria for judging algorithms that have a more direct
relationship to performance. These have to do with their computing
time and storage requirements.
[Space/Time complexity] The space complexity of an algorithm is the
amount of memory it needs to run to completion. The time complexity
of an algorithm is the amount of computer time it needs to run to
completion
Performance evaluation can be loosely divided into two major phases:
(1) a priori estimates and (2) a posteriori testing. We refer to these as
performance analysis and performance measurement respectively.](https://image.slidesharecdn.com/analysisofalgorithms1-240611062926-ee3f3756/85/Analysis-of-Algorithms-recurrence-relation-solving-recurrences-7-320.jpg)
Analysis of Algorithms, recurrence relation, solving recurrences
- 1. Introduction
- 2. Agenda • Introduction • Characteristics of an algorithm • Pseudocode conventions • Recursive algorithms • Performance analysis • Performance Measurement
- 3. Algorithm An algorithm is a finite set of instructions that,if followed, accomplishes a particular task. Characteristics of algorithms are as follows: 1. Input 2. Output 3. Definiteness 4. Finiteness 5. Effectiveness
- 4. Pseudocode Conventions 1. Comments // 2. Block of statements { and } 3. Identifiers 4. Assignment of values to variables 5. Boolean values 6. Multidimensional array 7. Looping statemets 8. Conditional statements 9. Input and output 10. Procedure
- 5. Recursive Algorithms A recursive function is a function that is defined in terms of itself. An algorithm is said to be recursive if the same algorithm is invoked in the body. An algorithm that calls itself is direct recursive. Algorithm A is said to be indirect recursive if it calls another algorithm which in turn calls A.
- 6. Example Write algorithm to print Fibonacci series for given number Write an algorithm to print factorial of given number Write an algorithm to print sum of array elements
- 7. Performance Analysis Aim of this course is to develop skills for making evaluative judgments about algorithm. There are two criteria for judging algorithms that have a more direct relationship to performance. These have to do with their computing time and storage requirements. [Space/Time complexity] The space complexity of an algorithm is the amount of memory it needs to run to completion. The time complexity of an algorithm is the amount of computer time it needs to run to completion Performance evaluation can be loosely divided into two major phases: (1) a priori estimates and (2) a posteriori testing. We refer to these as performance analysis and performance measurement respectively.
- 8. Space Complexity The space complexity of an algorithm is the amount of memory it needs to run to completion. The space needed by each algorithms is seen to be the sum of the following components: 1. A fixed part that is independent of the characteristics (e.g., number, size)of the inputs and outputs. This part typically includes the instruction space(i.e., space for the code), space for simple variables, space for constants, and soon. 2.A variable part that consists of the space needed by component variables whose size is dependent on the particular problem instance being solved, the space needed by referenced variables, the recursion stack space.
- 10. Time Complexity The time complexity of an algorithm is the amount of computer time it needs to run to completion. The time T(P) taken by a program P is the sum of the compile time and the run (or execution)time.
- 11. Example
- 12. Asymptotic Notations Analysis of algorithm is the process of analyzing the problem- solving capability of the algorithm in terms of the time and size required (the size of memory for storage while implementation). However, the main concern of analysis of algorithms is the required time or performance. Generally, we perform the following types of analysis − Worst-case − The maximum number of steps taken on any instance of size a. Best-case − The minimum number of steps taken on any instance of size a. Average case − An average number of steps taken on any instance of size a.
- 13. Asymptotic Analysis When analyzing the running time or space usage of programs, we usually try to estimate the time or space as function of the input size. For example, when analyzing the worst case running time of a function that sorts a list of numbers, we will be concerned with how long it takes as a function of the length of the input list. For example, we say the standard insertion sort takes time T(n) where T(n)= c*n2+k for some constants c and k. In contrast, merge sort takes time T ′(n) = c′*n*log2(n) + k′. Comp 122
- 14. Asymptotic Complexity Running time of an algorithm as a function of input size n for large n. Describes behavior of function in the limit. Written using Asymptotic Notation. Comp 122
- 15. O-notation Comp 122 g(n) is an asymptotic upper bound for f(n).
- 16. Examples 3n+2=O(n) 3n+2 <= c* n 3n+2 <= 4n for all n>=2 100n +6 =O(n) 100n + 6 <= 101n for all n>=6 Show that 3n3=O(n4) for appropriate c and n0. Comp 122
- 17. -notation Comp 122 g(n) is an asymptotically tight bound for f(n).
- 18. Example 3n +2 = (n) c1* n <= 3n +2 <= c2* n What constants for n0, c1, and c2 will work? Make c1 a little smaller than the leading coefficient, and c2 a little bigger. c1=3, c2=4, and n0=2 3*n<=3n+2<=4*n for all n>=2 Prove that 10n2 -3n=(n2) Prove that n2/2-3n= (n2) Comp 122
- 19. -notation Comp 122 g(n) is an asymptotic lower bound for f(n).
- 20. Example 3n + 2 = (n) 3n + 2>= c* n 3n +2>= 3n for all n>=0 n = (log n). Choose c and n0. Comp 122
- 21. Relations Between , O, Comp 122
- 22. Little oh o:
- 23. Little Omega ω
- 24. Ordered functions by their growth rates Comp 122
- 25. Comp 122
- 26. Recurrence Recurrences arise when an algorithm contains recursive calls to itself What is the actual running time of the algorithm? Need to solve the recurrence Find an explicit formula of the expression Bound the recurrence by an expression that involves n
- 27. Example Recurrences T(n) = T(n-1) + n Θ(n2) Recursive algorithm that loops through the input to eliminate one item T(n) = T(n/2) + c Θ(logn) Recursive algorithm that halves the input in one step T(n) = T(n/2) + n Θ(n) Recursive algorithm that halves the input but must examine every item in the input T(n) = 2T(n/2) + 1 Θ(n) Recursive algorithm that splits the input into 2 halves and does a constant amount of other work
- 28. Methods for Solving Recurrences Substitution method Recursion tree method Master method
- 29. The substitution method 1. Guess a solution 2. Use induction to prove that the solution works
- 30. Example T(n) = 2T(n/2) + 1 We guess that the solution is T(n)= O(n) The substitution method requires us to prove that T(n)<= c*n for an appropriate choice of the constant c>0 We start by assuming that this bound holds for all positive m<n in particular for m=n/2 T(n/2)<= cn/2 T(n) <= 2(cn/2) +1 <= cn + 1 <= cn
- 31. The recursion-tree method Convert the recurrence into a tree: Each node represents the cost incurred at various levels of recursion Sum up the costs of all levels
- 32. Example 1 32 W(n) = 2W(n/2) + n2 Subproblem size at level i is: n/2i Subproblem size hits 1 when 1 = n/2i i = lgn Cost of the problem at level i = (n/2i)2 No. of nodes at level i = 2i Total cost: W(n) = O(n2) 2 2 0 2 1 lg 0 2 lg 1 lg 0 2 2 ) ( 2 1 1 1 ) ( 2 1 2 1 ) 1 ( 2 2 ) ( n n O n n O n n n W n n W i i n i i n n i i
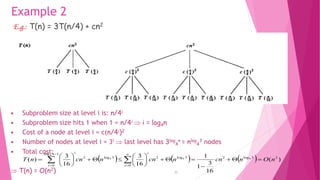
- 33. 33 Example 2 E.g.: T(n) = 3T(n/4) + cn2 • Subproblem size at level i is: n/4i • Subproblem size hits 1 when 1 = n/4i i = log4n • Cost of a node at level i = c(n/4i)2 • Number of nodes at level i = 3i last level has 3log 4 n = nlog 4 3 nodes • Total cost: T(n) = O(n2) ( ) ( ) ( ) ) ( 16 3 1 1 16 3 16 3 ) ( 2 3 log 2 3 log 2 0 3 log 2 1 log 0 4 4 4 4 n O n cn n cn n cn n T i i i n i
- 34. 34 Master’s method “Cookbook” for solving recurrences of the form: where, a ≥ 1, b > 1, and f(n) > 0 f(n) is asymptotically positive for all sufficiently large n. ) ( ) ( n f b n aT n T
- 35. 35 Master’s method “Cookbook” for solving recurrences of the form: where, a ≥ 1, b > 1, and f(n) > 0 Idea: compare f(n) with nlog b a Case 1: if f(n) = O(nlog b a -) for some > 0, then: T(n) = (nlog b a) Case 2: if f(n) = (nlog b a), then: T(n) = (nlog b a logn) Case 3: if f(n) = (nlog b a +) for some > 0, and if af(n/b) ≤ cf(n) for some c < 1 and all sufficiently large n, then: T(n) = (f(n)) ) ( ) ( n f b n aT n T regularity condition
- 36. 36 Examples T(n) = 2T(n/2) + n a = 2, b = 2, log22 = 1 Compare nlog 2 2 with f(n) = n f(n) = (n) Case 2 T(n) = (nlogn)
- 37. 37 Examples T(n) = 2T(n/2) + n2 a = 2, b = 2, log22 = 1 Compare n with f(n) = n2 f(n) = (n1+) Case 3 verify regularity cond. a f(n/b) ≤ c f(n) 2 n2/4 ≤ c n2 c = ½ is a solution (c<1) T(n) = (n2)