Bat algorithm explained. slides ppt pptx
- 1. Bat algorithm developed by Xin-shein 2010.
- 2. Outline 1- Bat Behaviour Some bats have evolved a highly sophisticated sense of hearing 2- Bat Algorithm This template is free to use under Creative Commons Attribution license. If you use the graphic assets (photos, icons and typographies) provided with this presentation you must keep the Credits slide.
- 3. Hello! I am Mahdi Atawneh You can find me at: @mshanak mahdi@ppu.edu
- 4. “This bat algorithm is based on the echolocation behaviour of micro bats with varying pulse rates of emission and loudness
- 6. ▷Echolocation: Some bats have evolved a highly sophisticated sense of hearing. Bat Behaviour
- 7. ▷ They emit sounds that bounce off of objects in their path, sending echoes back to the bats. Bat Behaviour
- 8. ▷ From these echoes, the bats can determine the size of objects, distance , how fast they are travelling. Bat Behaviour
- 10. Bat Behaviour
- 11. Bat Behaviour
- 12. 2. Bat Algorithm
- 13. Bat Algorithm - Rules 1. All bats use echolocation to sense distance, and they also `know' the difference between food/prey and background barriers.
- 14. Bat Algorithm - Rules 2. Bats fly randomly with ▷ velocity “vi” ▷ at position “Xi” ▷ with a fixed frequency “f” min , ▷ varying wavelength λ ▷ and loudness A0 to search for prey. They can automatically adjust the wavelength (or frequency) of their emitted pulses and adjust the rate of pulse emission “r” in the range of [0, 1], depending on the proximity of their target.
- 15. velocity “vi” position “Xi” frequency “f” wavelength λ loudness A0
- 16. Bat Algorithm - Rules 3. Although the loudness can vary in many ways, we assume that the loudness varies from a large (positive) “A0” to a minimum constant value “A min” .
- 17. Applications ▷engineering design ▷classifications of gene expression data ▷Protein Secondary Structure Prediction ▷A fuzzy bat clustering method has been developed to solve ergonomic workplace problems
- 18. 1 2 3 f = 3 x = 5 v = 4 A = 0,6 r = 0.3 f = 6 x = 8 v = 7 A = 0,3 r = 0.5 f = 2 x = 4 v = 3 A = 1 r = 0 Goal
- 20. pseudo code
- 21. t <MAXt Generate new solutions by adjusting frequency f, Update xi,vi Rand>ri Select a solution among the best solutions Generate a local solution around the selected best solution Generate a new solution by flying randomly initialize the bat population and vi Define pulse frequency fi at xi Initialize pulse rates ri and the loudness Ai Rand<Ai & F(xi)<f(x*) Accept the new solutions Increase ri reduce Ai Rank the bats and find the current best x∗ NO NO NO Postprocess results and visualization
- 22. t <MAXt Generate new solutions by adjusting frequency f, Update xi,vi Rand>ri Select a solution among the best solutions Generate a local solution around the selected best solution Generate a new solution by flying randomly initialize the bat population and vi Define pulse frequency fi at xi Initialize pulse rates ri and the loudness Ai Rand<Ai & F(xi)<f(x*) Accept the new solutions Increase ri reduce Ai Rank the bats and find the current best x∗ NO NO NO Postprocess results and visualization
- 23. t <MAXt Generate new solutions by adjusting frequency f, Update xi,vi Rand>ri Select a solution among the best solutions Generate a local solution around the selected best solution Generate a new solution by flying randomly initialize the bat population and vi Define pulse frequency fi at xi Initialize pulse rates ri and the loudness Ai Rand<Ai & F(xi)<f(x*) Accept the new solutions Increase ri reduce Ai Rank the bats and find the current best x∗ NO NO NO Postprocess results and visualization
- 24. t <MAXt Generate new solutions by adjusting frequency f, Update xi,vi Rand>ri Select a solution among the best solutions Generate a local solution around the selected best solution Generate a new solution by flying randomly initialize the bat population and vi Define pulse frequency fi at xi Initialize pulse rates ri and the loudness Ai Rand<Ai & F(xi)<f(x*) Accept the new solutions Increase ri reduce Ai Rank the bats and find the current best x∗ NO NO NO Postprocess results and visualization
- 25. example Assume that ▷F min=0 ▷F max =10
- 26. Initialize t=1 t=2 t=3 1 2 3 f = x = v = A = r = f = x = v = A = r = f = x = v = A = r =
- 27. Initialize (random) t=1 t=2 t=3 1 2 3 f = 3 x = v = A = 0,9 r = 0.1 f = 6 x = v = A = 0,8 r = 0.2 f = 2 x = v = A = 1 r = 0
- 28. Initialize (random) t=1 t=2 t=3 1 2 3 f = 3 x = 5 v = 4 A = 0,9 r = 0.1 f = 6 x = 8 v = 7 A = 0,8 r = 0.2 f = 2 x = 4 v = 3 A = 1 r = 0
- 29. Initialize (random) t=1 t=2 t=3 1 2 3 f = 3 x = 5 v = 4 A = 0,9 r = 0.1 f = 6 x = 8 v = 7 A = 0,8 r = 0.2 f = 2 x = 4 v = 3 A = 1 r = 0 1 2 3 f = 4 x = v = A = 0.9 r = 0.1 f = 3 x = v = A = 0.8 r = 0.2 f = 7 x = v = A = 1 r = 0
- 30. Initialize (random) t=1 t=2 t=3 1 2 3 f = 3 x = 5 v = 4 A = 0,9 r = 0.1 f = 6 x = 8 v = 7 A = 0,8 r = 0.2 f = 2 x = 4 v = 3 A = 1 r = 0 1 2 3 f = 4 x = v = A = 0.9 r = 0.1 f = 3 x = v = A = 0.8 r = 0.2 f = 7 x = 35 v = 31 A = 1 r = 0
- 31. Initialize (random) t=1 t=2 t=3 1 2 3 f = 3 x = 5 v = 4 A = 0,9 r = 0.1 f = 6 x = 8 v = 7 A = 0,8 r = 0.2 f = 2 x = 4 v = 3 A = 1 r = 0 1 2 3 f = 4 x = v = A = 0.9 r = 0.1 f = 3 x = v = A = 0.8 r = 0.2 f = 7 x = 35 v = 31 A = 1 r = 0 = 3 + (4-0) * 7 = 31
- 32. Initialize (random) t=1 t=2 t=3 1 2 3 f = 3 x = 5 v = 4 A = 0,9 r = 0.1 f = 6 x = 8 v = 7 A = 0,8 r = 0.2 f = 2 x = 4 v = 3 A = 1 r = 0 1 2 3 f = 4 x = v = A = 0.9 r = 0.1 f = 3 x = v = A = 0.8 r = 0.2 f = 7 x = 35 v = 31 A = 1 r = 0 = 4 + 31 = 35
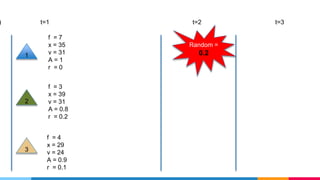
- 33. Initialize (random) t=1 t=2 t=3 1 2 3 f = 3 x = 5 v = 4 A = 0,9 r = 0.1 f = 6 x = 8 v = 7 A = 0,8 r = 0.2 f = 2 x = 4 v = 3 A = 1 r = 0 1 2 3 f = 4 x = 29 v = 24 A = 0.9 r = 0.1 f = 3 x = 39 v = 31 A = 0.8 r = 0.2 f = 7 x = 35 v = 31 A = 1 r = 0
- 34. t=2 t=3Initialize (random) t=1 1 2 3 f = 3 x = 5 v = 4 A = 0,9 r = 0.1 f = 6 x = 8 v = 7 A = 0,8 r = 0.2 f = 2 x = 4 v = 3 A = 1 r = 0 1 2 3 f = 4 x = 29 v = 24 A = 0.9 r = 0.1 f = 3 x = 39 v = 31 A = 0.8 r = 0.2 f = 7 x = 35 v = 31 A = 1 r = 0
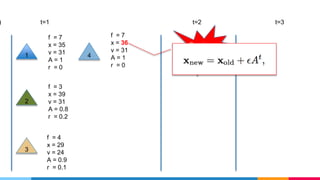
- 35. t=2 t=3) t=1 1 2 3 f = 4 x = 29 v = 24 A = 0.9 r = 0.1 f = 3 x = 39 v = 31 A = 0.8 r = 0.2 f = 7 x = 35 v = 31 A = 1 r = 0 Random = 0.2
- 36. t=2 t=3) t=1 1 2 3 f = 4 x = 29 v = 24 A = 0.9 r = 0.1 f = 3 x = 39 v = 31 A = 0.8 r = 0.2 f = 7 x = 35 v = 31 A = 1 r = 0 Random = 0.2 Compare
- 37. t=2 t=3) t=1 1 2 3 f = 4 x = 29 v = 24 A = 0.9 r = 0.1 f = 3 x = 39 v = 31 A = 0.8 r = 0.2 f = 7 x = 35 v = 31 A = 1 r = 0 Random = 0.24 f = 7 x = v = 31 A = 1 r = 0
- 38. t=2 t=3) t=1 1 2 3 f = 4 x = 29 v = 24 A = 0.9 r = 0.1 f = 3 x = 39 v = 31 A = 0.8 r = 0.2 f = 7 x = 35 v = 31 A = 1 r = 0 Random = 0.24 f = 7 x = 36 v = 31 A = 1 r = 0
- 39. t=2 t=3) t=1 1 2 3 f = 4 x = 29 v = 24 A = 0.9 r = 0.1 f = 3 x = 39 v = 31 A = 0.8 r = 0.2 f = 7 x = 35 v = 31 A = 1 r = 0 Random = 0.24 f = 7 x = 36 v = 31 A = 1 r = 0
- 40. t=2 t=3) t=1 1 2 3 f = 4 x = 29 v = 24 A = 0.9 r = 0.1 f = 3 x = 39 v = 31 A = 0.8 r = 0.2 f = 7 x = 35 v = 31 A = 1 r = 0 Random = 0.24 f = 7 x = 36 v = 31 A = 1 r = 0 6 f = 5 x = 7 v = 6 A = .7 r = .2 Random Solution
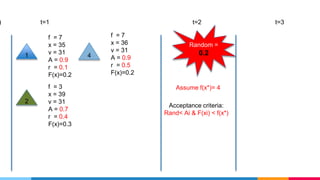
- 41. t=2 t=3) t=1 1 2 3 f = 4 x = 29 v = 24 A = 0.9 r = 0.3 F(x)=0.4 f = 3 x = 39 v = 31 A = 0.8 r = 0.3 F(x)=0.3 f = 7 x = 35 v = 31 A = 1 r = 0 F(x)=0.2 Random = 0.24 f = 7 x = 36 v = 31 A = 1 r = 0.4 F(x)=0.2 6 f = 5 x = 7 v = 6 A = .7 r = .2 F(x)=0.6 Random Solution Assume f(x*)= 4 Acceptance criteria: Rand< Ai & F(xi) < f(x*)
- 42. t=2 t=3) t=1 1 2 3 f = 4 x = 29 v = 24 A = 0.1 r = 0.3 F(x)=0.4 f = 3 x = 39 v = 31 A = 0.8 r = 0.3 F(x)=0.3 f = 7 x = 35 v = 31 A = 1 r = 0 F(x)=0.2 Random = 0.24 f = 7 x = 36 v = 31 A = 1 r = 0.4 F(x)=0.2 6 f = 5 x = 7 v = 6 A = .7 r = .2 F(x)=0.6 Random Solution Assume f(x*)= 4 Acceptance criteria: Rand< Ai & F(xi) < f(x*)
- 43. t=2 t=3) t=1 1 2 f = 3 x = 39 v = 31 A = 0.8 r = 0.3 F(x)=0.3 f = 7 x = 35 v = 31 A = 1 r = 0 F(x)=0.2 Random = 0.24 f = 7 x = 36 v = 31 A = 1 r = 0.4 F(x)=0.2 Assume f(x*)= 4 Acceptance criteria: Rand< Ai & F(xi) < f(x*)
- 44. t=2 t=3) t=1 1 2 f = 3 x = 39 v = 31 A = 0.7 r = 0.4 F(x)=0.3 f = 7 x = 35 v = 31 A = 0.9 r = 0.1 F(x)=0.2 Random = 0.24 f = 7 x = 36 v = 31 A = 0.9 r = 0.5 F(x)=0.2 Assume f(x*)= 4 Acceptance criteria: Rand< Ai & F(xi) < f(x*)
- 45. t=2 t=3) t=1 1 2 f = 3 x = 39 v = 31 A = 0.7 r = 0.4 F(x)=0.3 f = 7 x = 35 v = 31 A = 0.9 r = 0.1 F(x)=0.2 Random = 0.24 f = 7 x = 36 v = 31 A = 0.9 r = 0.5 F(x)=0.2 Assume f(x*)= 4 Acceptance criteria: Rand< Ai & F(xi) < f(x*) Select best X* X*=1
- 46. “Thanks













![Bat Algorithm - Rules
2.
Bats fly randomly with
▷ velocity “vi”
▷ at position “Xi”
▷ with a fixed frequency “f” min ,
▷ varying wavelength λ
▷ and loudness A0 to search for prey.
They can automatically adjust the wavelength (or frequency) of their emitted
pulses and adjust the rate of pulse emission “r” in the range of [0, 1],
depending on the proximity of their target.](https://image.slidesharecdn.com/batalgorithm-160503134011/85/Bat-algorithm-explained-slides-ppt-pptx-14-320.jpg)