А. Зиновьев "Big data algorithms and data structures for large scale graphs", DUMP-2014
2 likes1,231 views
Доклад посвящен алгоритмам и структурам данных для обработки больших графов, рассматривая применение теории графов в различных областях, таких как социология и транспортные системы. Обсуждаются современные методы обработки графов, включая алгоритмы для поиска кратчайших путей и системы для вычислений на больших графах, такие как Pregel и Giraph. Кроме того, отмечается важность оптимизации хранения данных и устойчивости алгоритмов к ошибкам в условиях высокой вероятности возникновения сбоев.
![Алгоритмы для вычисления
кратчайшего расстояния
ALT: [Goldberg & Harrelson 05], [Delling & Wagner 07]
RE: [Gutman 05], [Goldberg et al. 07]
HH: [Sanders & Schultes 06]
CH: [Geisberger et al. 08]
TN: [Geisberger et al. 08]
HL: [Abraham et al. 11]
Dijkstra ALT RE HH CH TN HL
2 008 300 24 656 2444 462.0 94.0 1.8 0.3](https://image.slidesharecdn.com/bigdataalgorithmsanddatastructuresforlarge-scalegraphs-140331011359-phpapp01/85/Big-data-algorithms-and-data-structures-for-large-scale-graphs-DUMP-2014-46-320.jpg)
А. Зиновьев "Big data algorithms and data structures for large scale graphs", DUMP-2014
- 1. Докладчик: Алексей Зиновьев Big Data algorithms and data structures for large-scale graphs
- 2. О себе ● аспирант ОмГУ, математик ● занимаюсь теорией графов, прогнозированием пробок, исследованием транспортных систем ● большой фанат различных Maps API
- 3. BigData & Graph Theory
- 4. Откуда BigData есть быти? BigData прошлого: ● Астрономический вычисления ● Данные многолетних наблюдений за погодой ● Данные торговых операций ● Морские маршруты
- 5. А теперь ● Web-граф (модель Интернета) ● Граф почтовых сообщений ● Социологические исследования ● Дорожные графы ● Транзакции на PayPal ● Граф друзей на Facebook ● Анализ текстов, публикаций
- 8. Чемпионы-тяжеловесы Граф Число вершин Число ребер Объем данных на диске Прирост в день Web-граф 1 трлн 8 трлн 100 PB 300 TB Facebook (граф друзей) 1 млрд 140 млрд 1 PB 15 TB Дорожный граф Европы 18 млн 42 млн 20 GB 50 MB Дорожный графЕкб 120 000 260 000 400 MB 100 KB
- 9. ● найти ближайшую точку к данной на большом множестве точек; ● расcтояние может быть любым, в том числе быть длиной кратчайшего маршрута на графе. Основные приложения ● сервисы рекомендаций, генетические исследования; ● распознавание образов; ● классификация текстов; ● рекомендательные и экспертные системы; ● динамическое размещение рекламы в Интернете. Nearest Neighbor Search (NNS)
- 11. Эксперимент Милграма ● Hyper ANF - новый алгоритм, основанный на счетчиках HyperLogLog и вычислении функции соседства ● HyperLogLog - статистический счетчик (6% отклонение, 5 - 7 bits) ● Диаметр Facebook - 10 hours, 1TB RAM Facebook 4.74 712 M 69 G Twitter 3.67 ---- 5G follows MSN Messenger (1 month) 6.6 180 M 1.3 G arcs
- 12. ● поиск кратчайшего расстояния между двумя точками ● кластеризация и поиск компонент ● поиск min/max остовного дерева ● задача коммивояжера ● потоковые задачи ● построение моделей динамических графов, развивающихся схоже с некоторыми реальными совокупностями объектов (человечество; все научные статьи; преступления; почтовая переписка) Основные задачи на графах
- 15. Node Centrality Problem Зачем искать множество центральных точек? ● влияние таких точек больше остальных ● удаление важных вершин снижает надежность системы Основные приложения ● астрофизика ● биоинформатика ● социальные связи ● дорожные сети ● изучение топологии интернета и выявление спама ● системы рекомендаций
- 17. ● матрица смежности ● матрица инцидентности ● список смежных вершин ● список ребер ● различные виды деревьев ● в виде стеков и многие другие... Все эти представления различаются по потребляемой памяти и временной сложности выполнения стандартных операций над графом. Традиционные и не очень структуры данных
- 18. ● граф в RAM, данные на диске в свободном формате ● граф в RAM, данные в неграфовой СУБД ● граф в RAM, данные в графовой СУБД ● граф не загружается целиком в RAM, обработка идет частями, данные на диске в произвольном формате ● неграфовое представление в RAM, данные на диске в файле или в СУБД любого типа Для некоторых агрегационных вычислений граф не требуется представлять в памяти в виде графа и определять корректные операции Способы работы с графом
- 19. ● Оптимальна для сильносвязных сущностей ● Вершины, ребра, атрибуты ● Индексы на значения атрибутов ● ACID ● REST API + Cypher ● Множество плагинов, включая 2d индекс Neo4j: преимущества
- 21. ● Нет полноценного горизонтального масштабирования ● Плохо приспособлен для размещения на нескольких машинах ● Лимиты и платность ● Много маркетинга и неоправданного использования Neo4j: недостатки
- 22. Системы для вычисления на больших графах
- 23. Решение некоторых графовых задач при помощи MapReduce возможно, но не является оптимальным ● сложность сведения графовой задачи к модели key- value ● большинство графовых алгоритмов построено на итерационной обработке, что в M/R требует multiple chained jobs, что влечет полное сохранение и загрузку состояния графа (эта операция будет доминировать по времени) Think like a vertex… Ограничения парадигмы MapReduce
- 25. Определим две базовых операции ● Fusion - собираем информацию от соседей ● Diffusion - распостраняем информацию от вершины соседям Храним состояние графа в памяти в течение всей обработки, сохраняя только конечное состояние и некоторые промежуточные точки прогресса. Теперь вместо определения mapper и reducer, достаточно определить Vertex, который имеет значение и список ребер, а также способен посылать сообщения на каждой итерации. Bulk Synchronous Parallel
- 27. Pregel - система для вычислений на больших графах В основе Pregel лежит вершинный подход, а сама система основана на модели Bulk Synchronous Parallel Программы обработки графов в Pregel представлены в виде последовательностей итераций, которые называются супершагами. При выполнении супершага для каждой вершины графа запускается определенная пользователем функция, и все функции выполняются параллельно.
- 28. Pregel - система для вычислений на больших графах
- 29. Pregel - система для вычислений на больших графах Вершины обмениваются сообщениями, а также могут изменять свое состояние и состояние смежных ребер, согласно полученной информации. Если вершина не получила сообщений, то она становится неактивной. Если все вершины не активны, то работа алгоритма останавливается. Pregel обеспечивает масштабируемость, устойчива к ошибкам и позволяет применять произвольные алгоритмы.
- 30. С++ API
- 32. Giraph - открытая система для вычислений на больших графах В основе Giraph лежат статьи Google о построении собственной системы Pregel. В свое время использовался в Facebook для анализа социального графа. В данный момент в Giraph добавлено несколько фич, которых нет в Pregel: master computation, sharded aggregators, edge-oriented input, out-of-core computation
- 33. Giraph - открытая система для вычислений на больших графах В данный момент доступна версия 1.0 В основе лежит модель Master/Workers, где ● Master - распределяет куски данных между Workers и синхронизирует супершаги ● Worker - загружает свой кусок графа и выполняет все вычисления, рассылает сообщения Нет точки отказа, т.к. при падении текущего Master, на его место заступает другой. При падении Worker вычисления начинаются с последней checkpoint с меньшим количеством workers. Очередь из “заместителей” Master хранится в ZooKeeper
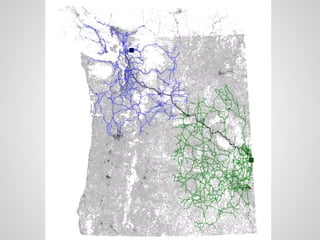
- 35. Дорожные графы
- 36. Не всякий граф - дорожный... Назовем граф дорожным, если он может быть описан как граф с положительными весами, приписанными к ребрам. Также часть ребер в таком графе может быть более важной, чем остальная (магистральные шоссе, выделенные линии связи). Это свойство может использоваться в различных алгоритмах на “дорожных” графах, чтобы вычислять кратчайшие расстояния быстрее, чем на обычных графах.
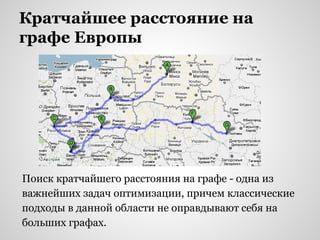
- 37. Кратчайшее расстояние на графе Европы Поиск кратчайшего расстояния на графе - одна из важнейших задач оптимизации, причем классические подходы в данной области не оправдывают себя на больших графах.
- 40. A* - эвристический алгоритм Каким образом можно улучшить алгоритм Дейкстры и не просматривать целиком весь граф в процессе построения кратчайшего маршрута? Алгоритм поиска по первому наилучшему совпадению (best first) на графе, который находит маршрут с наименьшей стоимостью между двумя вершинами Порядок обхода вершин определяется эвристической функцией «расстояние + стоимость» (обычно обозначаемой как f(v)= g(v) + h(v))
- 42. Двунаправленный поиск Алгоритм состоит: ● прямого поиска, аналогичного одиночному поиску; ● обратного поиска; ● операции определения принадлежности листа другому дереву поиска. Соединив пути получаем искомый путь. Если два поиска осуществляются параллельно — это ещё больше экономит время на получение искомого пути по сравнению с однонаправленным поиском.
- 44. Требования к системе обработки ● Необходимо быстро (10 мс) находить кратчайшее расстояние между двумя точками ● Линейность алгоритмов ● Этап предварительной обработки (препроцессинг) ● Не хранить все расстояния между вершинами (O(n^2) по памяти) ● Ответ может быть точным с определенной вероятностью ● Учет геоспецифики графа ● Использование сжатия и перекодировки для хранения на диске
- 45. Двухфазовые алгоритмы Все подобные алгоритмы работают в два этапа. Первый этап включает в себя предварительную обработку графа без использования информации о том, между какими вершинами надо найти кратчайшее расстояние. Результаты обработки сохраняются в базу данных. Второй этап - выполнение запроса к базе данных. В момент выполнения запроса известны узлы, между которыми необходимо найти кратчайшее расстояние. Основное предположение состоит в том, что дорожная сеть слабо изменяется со временем и фазу обработки не нужно выполнять слишком часто.
- 46. Алгоритмы для вычисления кратчайшего расстояния ALT: [Goldberg & Harrelson 05], [Delling & Wagner 07] RE: [Gutman 05], [Goldberg et al. 07] HH: [Sanders & Schultes 06] CH: [Geisberger et al. 08] TN: [Geisberger et al. 08] HL: [Abraham et al. 11] Dijkstra ALT RE HH CH TN HL 2 008 300 24 656 2444 462.0 94.0 1.8 0.3
- 47. A* with landmarks (ALT) ● Выбираем подмножество вершин (случайно, например) ● Вычисляем расстояния между ними ● Вычисление нижних границ (функции h(v)) для A* расстояний между ними происходит за O(1) Поиск может быть направлен с двух сторон. Низкий уровень сканирования: для того чтобы найти путь из 1000 вершин в графе с 3 млн, было просканировано всего 10 тысяч вершин.
- 49. Reach (RE) Формализуем интуицию автомобилиста: ● он не ищет объезд вдалеке ● он стремится попасть поскорее но основную скоростную магистраль ● он стремится гнать по основной магистрали, не обращая внимание на дороги меньшего класса важности, двигаясь по направлению к цели
- 51. Contraction hierarchies (CH) Это техника для поиска кратчайших путей в созданном на предварительной стадии особом “контрактном” графе. Дуга может быть пропущена, если есть альтернативные пути. Большую роль играет класс и важность дороги. Для поиска в новом графе используется двунаправленный алгоритм Дейкстры.
- 52. Transit nodes (TN) Граф разбивается на подграфы так, что для каждого подграфа, есть небольшой набор узлов R, таких, что все кратчайшие пути между вершинами* из региона проходят через узел из R. Фаза препроцессинга: ● найти R для каждого региона ● найти для каждой вершины его transit node из R ● вычислить все пары кратчайших путей между транзитными узлами из R * больше определенной величины d
- 55. Оптимизационные задачи на больших графах Однако, при решении оптимизационных задач на графах, изменяющих структуру самого графа, фаза препроцессинга длиною в несколько часов становится бессмысленной. Пример задачи: есть 1 млрд рублей на развитие дорожной сети. Каким образом можно инвестировать его, чтобы уменьшить среднее время, затрачиваемое на ежедневные межрайонные корреспонденции граждан? Еще пример: дорожная сеть подверглась воздействию стихии, ожидается еще один удар. Где проложить новые дороги, чтобы система была максимально устойчивой?
- 61. I/O Efficient Algorithms and Data Structures ● Традиционный подход состоит в случайном чтении из RAM ● Однако, стоит помнить, что уровней памяти много ● Чем дальше от CPU, тем больше и медленнее ● Данные перемещаются между уровнями большими блоками ● Часто OS берет на себя предсказание и подгрузку ● Диск в 10^6 медленнее RAM ● Разбиение на небольшие блоки и выполнение операций внутри каждого блока с объединением результата уменьшает число I/O операций
- 62. Graphs and Memory Errors Что может привести к ошибкам? ● космическое излучение ● битый кусок винчестера ● ошибка при передаче данных из RAM в кэш Чем чревато? ● классические алгоритмы (слияние списков, например) не готовы к ошибкам ● выходом из строя критического оборудования ● редкость ошибок - миф (эксперимент Google) Разработка алгоритмов, устойчивых к ошибкам, ведется уже 50 лет!
- 63. Итоги ● Для анализа большого графа достаточно небольшого вычислительного кластера ● Структуры данных и способ хранения очень сильно зависят от задачи и выбранного алгоритма ● Невозможна хаотичная работа с большими данными без соответствующего математического аппарата и программного обеспечения