![Ex 2 p. 167 Find extrema of on [-1,2] Need derivative to find critical numbers: What values of x make f’ = 0 or f’ be undefined? Evaluate f at critical numbers Evaluate f at endpoints 4. So f(1) = -1 is minimum and f(2)=16 is maximum. Left endpoint Critical number Critical number Right endpoint f(-1) = 7 f(0) = 0 f(1) = -1 minimum f(2) = 16 maximum](https://image.slidesharecdn.com/calc3-1-111012215200-phpapp01/85/Calc-3-1-11-320.jpg)
![Ex 3 p. 168 Find extrema of on [-1, 3] 1. Find critical numbers. Two critical numbers, x = 0 because that makes f’ undefined and it doesn’t exist, and x = 1 because that makes f’ = 0 2&3. Evaluate f at critical numbers and endpoints 4. Determine max and min for interval. Left endpoint Critical number Critical number Right endpoint f(-1) = -5 Minimum f(0) = 0 Maximum f(1) = -1 f(3) ≈-0.24](https://image.slidesharecdn.com/calc3-1-111012215200-phpapp01/85/Calc-3-1-13-320.jpg)
![Ex 4 p. 168 Finding Extrema on a closed interval Find the extrema of f(x) = 2sin x – cos 2x on [0, 2 π ] 1. Critical numbers: 2&3. Plug in endpoints and critical numbers 4. Determine maximum and minimum Left endpt Critical # Critical # Critical # Critical # Right endpt f(0) = -1 f( π /2) = 3 Maximum f(7 π /6) = -1.5 minimum f(3 π /2)=-1 f(11 π /6) =-1.5 mimumum f(2 π ) = -1](https://image.slidesharecdn.com/calc3-1-111012215200-phpapp01/85/Calc-3-1-15-320.jpg)
Calc 3.1
- 1. 3.1 Extrema on an Interval
- 2. A lot of effort goes into determining the behavior of a function f on an interval I . Does it have a maximum in the interval? Where is it increasing, decreasing? p. 164
- 3. A function need not have a maximum or minimum in an interval.
- 4. You can see that continuity or discontinuity can affect the existence of an extremum on an interval. This suggests this theorem: Notice that this theorem guarantees a minimum and maximum, but doesn’t help you find them! p. 164
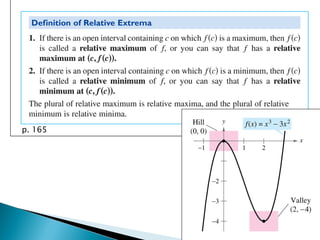
- 5. p. 165
- 6. Example 1, p. 165 Find the value of the derivative at each of the relative extrema shown: a. At the point (3, 2), f’(3) = 0
- 7. f(x) = |x| These two one-sided limits disagree, so derivative doesn’t exist at (0, 0)
- 8. The derivative of f(x) = sin x is f’ = cos x. At the point ( π /2, 1) the derivative is f’( π /2) = cos ( π /2)=0 At the point (3 π /2, -1), f’(3 π /2) = cos (3 π /2)= 0
- 9. We can see that at relative extrema, the derivative is either zero or does not exist. The x-values of these extrema are called critical numbers. There are two types. p. 166
- 10. p. 166
- 11. Ex 2 p. 167 Find extrema of on [-1,2] Need derivative to find critical numbers: What values of x make f’ = 0 or f’ be undefined? Evaluate f at critical numbers Evaluate f at endpoints 4. So f(1) = -1 is minimum and f(2)=16 is maximum. Left endpoint Critical number Critical number Right endpoint f(-1) = 7 f(0) = 0 f(1) = -1 minimum f(2) = 16 maximum
- 12. Notice that all critical numbers don’t have to produce extrema. Converse of Thm 3.2 is not necessarily true! In other words, if x=c is a critical number, f doesn’t have to have a relative max or min there.
- 13. Ex 3 p. 168 Find extrema of on [-1, 3] 1. Find critical numbers. Two critical numbers, x = 0 because that makes f’ undefined and it doesn’t exist, and x = 1 because that makes f’ = 0 2&3. Evaluate f at critical numbers and endpoints 4. Determine max and min for interval. Left endpoint Critical number Critical number Right endpoint f(-1) = -5 Minimum f(0) = 0 Maximum f(1) = -1 f(3) ≈-0.24
- 15. Ex 4 p. 168 Finding Extrema on a closed interval Find the extrema of f(x) = 2sin x – cos 2x on [0, 2 π ] 1. Critical numbers: 2&3. Plug in endpoints and critical numbers 4. Determine maximum and minimum Left endpt Critical # Critical # Critical # Critical # Right endpt f(0) = -1 f( π /2) = 3 Maximum f(7 π /6) = -1.5 minimum f(3 π /2)=-1 f(11 π /6) =-1.5 mimumum f(2 π ) = -1
- 17. Assignment 3.1 p. 169/ 1-45 every other odd, 53-59 odd, 63-66 due Wednesday, Oct 19