Codes: Binary Codes Weighted codes Binary Coded Decimal (BCD) Non-weighted codes Excess – 3 code, Gray code, Alphanumeric codes – ASCII Code, EBCDIC, ISCII Code, Error detectionCodes.pdf
- 1. Codes -
- 2. DLCA Bharati Ingale (bharatijingale@gmail.com) Objective Binary Codes Weighted codes Binary Coded Decimal (BCD) Non-weighted codes Excess – 3 code, Gray code, Alphanumeric codes – ASCII Code, EBCDIC, ISCII Code, Error detection
- 3. DLCA Bharati Ingale (bharatijingale@gmail.com) Binary Codes Computers and digital circuits processes information in the binary format. Each character is assigned 7 or 8 bit binary code to indicate its character which may be numeric, alphabet or special symbol.
- 4. DLCA Bharati Ingale (bharatijingale@gmail.com) Binary Codes Numbers, letters or words are represented by a specific group of symbols is called a code. Here the number, letter or word is said to be encoded. Example - Binary number 1000001 represents 65(decimal) in straight binary code, alphabet A in ASCII code and 41(decimal) in BCD code.
- 5. DLCA Bharati Ingale (bharatijingale@gmail.com) Binary Codes The digital data is represented, stored and transmitted as group of binary bits. This group is also called as binary code. The binary code is represented by the number as well as alphanumeric letter.
- 6. DLCA Bharati Ingale (bharatijingale@gmail.com) Advantages of Binary Code Binary codes are suitable for both the computer applications. the digital communications. Binary codes make the analysis and designing of digital circuits easier if binary codes are used. Since only 0 & 1 are being used, implementation becomes easy.
- 7. DLCA Bharati Ingale (bharatijingale@gmail.com) Classification of binary codes Codes Weighted Codes Non weighted Codes Reflective Sequential Alphanumeric Error Detection & Correcting Codes
- 8. DLCA Bharati Ingale (bharatijingale@gmail.com) Classification of binary codes Codes Weighted Codes BCD Codes 8421 2421 Non weighted Codes Gray code Excess 3 code Alphanumeric Codes ASCII Code EBDCIC (Extended binary coded decimal interchange code) Error Detecting/ Correcting Codes Parity Bit Hamming Bit
- 9. DLCA Bharati Ingale (bharatijingale@gmail.com) Classification of binary codes Codes Weighted Codes BCD Codes 8421 2421 Non weighted Codes Gray code Excess 3 code Alphanumeric Codes ASCII Code EBDCIC (Extended binary coded decimal interchange code) Error Detecting/ Correcting Codes Parity Bit Hamming Bit
- 10. DLCA Bharati Ingale (bharatijingale@gmail.com) Weighted Codes Weighted binary codes are those binary codes which obey the positional weight principle. Each position of the number represents a specific weight. Several systems of the codes are used to express the decimal digits 0 through 9. Eg: 8421 & 2421 In these codes each decimal digit is represented by a group of four bits.
- 11. DLCA Bharati Ingale (bharatijingale@gmail.com) Weighted Codes 2+4+2+1 2+4+2+1
- 12. DLCA Bharati Ingale (bharatijingale@gmail.com) Classification of binary codes Codes Weighted Codes BCD Codes 8421 2421 Non weighted Codes Gray code Excess 3 code Alphanumeric Codes ASCII Code EBDCIC (Extended binary coded decimal interchange code) Error Detecting/ Correcting Codes Parity Bit Hamming Bit
- 13. DLCA Bharati Ingale (bharatijingale@gmail.com) Binary Coded Decimal (BCD) code In this code each decimal digit is represented by a 4-bit binary number. BCD is a way to express each of the decimal digits with a binary code. In the BCD, with four bits we can represent sixteen numbers (0000 to 1111). But in BCD code only first ten of these are used (0000 to 1001). The remaining six code combinations i.e. 1010 to 1111 are invalid in BCD.
- 14. DLCA Bharati Ingale (bharatijingale@gmail.com) Binary Coded Decimal (BCD) code Conversion of decimal numbers to BCD To express any decimal number in BCD, simply express each decimal digit with its equivalent 4-bit BCD code. (98)10 = (1001 1000) BCD
- 15. DLCA Bharati Ingale (bharatijingale@gmail.com) Smallest and Largest Digit in BCD The smallest digit in BCD is 0000 i.e 0 and The largest digit in BCD is 1001 i.e 9 Codes
- 16. DLCA Bharati Ingale (bharatijingale@gmail.com) Binary to BCD Conversion Steps Step 1 -- Convert the binary number to decimal. Step 2 -- Convert decimal number to BCD. Codes
- 17. DLCA Bharati Ingale (bharatijingale@gmail.com) Binary to BCD Conversion Example − convert (11101)2 to BCD. Step 1 − Convert to Decimal Binary Number − 111012 111012 = ( 1 × 24 + 1 × 23 + 1 × 22 + 0 × 21 + 1 × 20 )10 = (16 + 8 + 4 + 0 + 1)10 = 2910 Codes
- 18. DLCA Bharati Ingale (bharatijingale@gmail.com) BCD code Binary Number − 111012 = Decimal Number − 2910 Step 2 − Convert to BCD i. Decimal Number − 2910 ii. Calculate BCD Equivalent.: Convert each digit into groups of four binary digits equivalent. (11101)2 = (0010 1001)BCD
- 19. DLCA Bharati Ingale (bharatijingale@gmail.com) BCD to Binary Conversion Steps Step 1 -- Convert the BCD number to decimal. Step 2 -- Convert decimal to binary. BCD Code
- 20. DLCA Bharati Ingale (bharatijingale@gmail.com) BCD to Binary Conversion Example − convert (00101001)BCD to Binary. Step 1 - Convert the BCD number to decimal BCD Number − (01111001)BCD = Decimal 79 BCD Number − (00101001)BCD = Decimal Number − 2910 Step 2 - Convert to Decimal to Binary Decimal Number − 7810 Calculating Binary Equivalent −10011102 BCD Code
- 21. DLCA Bharati Ingale (bharatijingale@gmail.com) Binary Coded Decimal (BCD) code Packed BCD number Representation of Decimal Number beyond 9 is called Packed BCD Eg: (156)10 = (0001 0101 0110)packed BCD
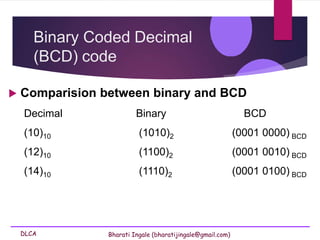
- 22. DLCA Bharati Ingale (bharatijingale@gmail.com) Binary Coded Decimal (BCD) code Comparision between binary and BCD Decimal Binary BCD (10)10 (1010)2 (0001 0000) BCD (12)10 (1100)2 (0001 0010) BCD (14)10 (1110)2 (0001 0100) BCD
- 23. DLCA Bharati Ingale (bharatijingale@gmail.com) 1 1 1 1 0 1 1 0 + 1 0 1 0 1 1 1 0 1 (1100)Binary 0001 0010
- 24. DLCA Bharati Ingale (bharatijingale@gmail.com) Binary Coded Decimal (BCD) code Advantages of BCD Codes It is very similar to decimal system. We need to remember binary equivalent of decimal digits 0 to 9 only. Disadvantages of BCD Codes BCD needs more number of bits than binary to represent the decimal number. So BCD is less efficient than binary.
- 25. DLCA Bharati Ingale (bharatijingale@gmail.com) Application: 7-segment display One popular type of decimal display is the 7 segment display used in LED and LCD numerical displays, where any decimal digit is made up of 7 segments arranged as a figure. BCD Code These displays therefore require 7 inputs, one to each of the LEDs a to g. Therefore the 4 bit output in BCD must be converted to supply the correct 7 bit pattern of outputs to drive the display.
- 26. DLCA Bharati Ingale (bharatijingale@gmail.com) BCD Code
- 27. DLCA Bharati Ingale (bharatijingale@gmail.com) Non-Weighted Codes In this type of binary codes, the positional weights are not assigned. The examples of non-weighted codes are Excess-3 code Gray code
- 28. Excess-3 code
- 29. DLCA Bharati Ingale (bharatijingale@gmail.com) 16.1 Excess-3 code The Excess-3 code is also called as XS-3 code. It is non-weighted code used to express decimal numbers. The Excess-3 code words are derived from the 8421 BCD code words adding (0011)2 or (3)10 to each code word in 8421. The excess-3 codes are obtained as follows −
- 30. Conversion Table
- 31. DLCA Bharati Ingale (bharatijingale@gmail.com) Binary Coded Decimal (BCD) code Properties of excess – 3 codes Each codeword is equivalent to its decimal value plus 3 in binary. The codewords for 0–4 are complements of the codewords 5–9.
- 32. Examples 12 to excess -3 = 1+3 = 4 2+3 = 5 0 0 0 1 0 0 1 0 0 0 1 1 0 0 1 1 0 1 0 0 0 1 0 1 29 to excess -3 = 2+3 = 5 9+3 = 12 1 + 3 4 0 1 0 0 2 + 3 5 0 1 0 1 2 + 3 0 5 0 1 0 1 9 + 3 1 2 1 1 0 0 Convert the following numbers to Excess – 3 code
- 33. Examples 8 + 3 1 1 1 0 1 1 7 + 3 1 0 1 0 1 0 Convert the following numbers to Excess – code 1. 87 2. 159 Solution: 1. 87
- 34. Examples 5 + 3 8 1 0 0 0 9 + 3 1 1 1 0 1 1 1 + 3 4 0 1 0 0 Convert the following numbers to Excess – code 1. 87 2. 159 Solution: 2. 159
- 35. DLCA Bharati Ingale (bharatijingale@gmail.com) Convert Excess-3 code into BCD and decimal number. 1. Group 4-bit for each group, and 2. Subtract 0011 from given number to get the BCD code 3. Find the decimal equivalent. Excess-3 code
- 36. DLCA Bharati Ingale (bharatijingale@gmail.com) Convert Excess-3 code 1001001 into BCD and decimal number. Excess-3 code 1. Group 4-bit for each group, and 2. Subtract 0011 from given number to get the BCD code 3. Find the decimal equivalent. 0 1 0 0 1 0 0 1 - 0 0 1 1 0 0 1 1 0 0 0 1 0 1 1 0 1 6 Binary Coded Decimal number is 0001 0110 and decimal number will be 16.
- 37. Gray Code
- 38. DLCA Bharati Ingale (bharatijingale@gmail.com) Gray Code It is the non-weighted code It is not arithmetic codes. That means there are no specific weights assigned to the bit position. It has a very special feature that, only one bit will change each time the decimal number is incremented.. As only one bit changes at a time, the gray code is called as a unit distance code.
- 39. DLCA Bharati Ingale (bharatijingale@gmail.com) Gray Code The gray code is a cyclic code. Also called as the reflected binary code The reflected binary code or Gray code is an ordering of the binary numeral system such that two successive values differ in only one bit (binary digit). Gray code cannot be used for arithmetic operation.
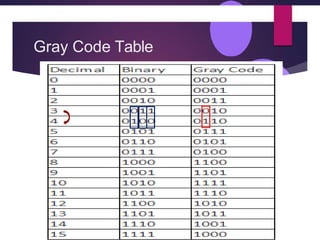
- 40. Gray Code Table
- 41. Gray Code Table
- 42. DLCA Bharati Ingale (bharatijingale@gmail.com) Gray code also known as reflected binary code, because the first (n/2) values compare with those of the last (n/2) values, but in reverse order. Gray code
- 43. DLCA Bharati Ingale (bharatijingale@gmail.com) Gray code exhibits the reflective property i.e the 2 LSB for decimal 4 to 7 are the mirror images of those for decimal 3 to 0 Gray code Mirror
- 44. DLCA Bharati Ingale (bharatijingale@gmail.com) Decima l G(4) G(3) G(2) G(1) G(4) G(3) G(2) G(1) 0 0 0 0 0 x 0 0 0 1 0 0 0 1 x 0 0 1 2 0 0 1 1 x 0 1 1 3 0 0 1 0 x 0 1 0 4 0 1 1 0 x 1 1 0 5 0 1 1 1 x 1 1 1 6 0 1 0 1 x 1 0 1 7 0 1 0 0 x 1 0 0 8 1 1 0 0 x 1 0 0 9 1 1 0 1 x 1 0 1 10 1 1 1 1 x 1 1 1 11 1 1 1 0 x 1 1 0 12 1 0 1 0 x 0 1 0 13 1 0 1 1 x 0 1 1 14 1 0 0 1 x 0 0 1 15 1 0 0 0 x 0 0 0 4-bit Binary to Gray Truth table Mirror the 3 LSB for decimal 8 to 15 are the mirror images of those for decimal 7 to 0
- 45. DLCA Bharati Ingale (bharatijingale@gmail.com) Binary to Gray Code conversion (Addition) Steps Step 1 – Record the MSB as it is Step 2 – Add MSB to the next bit, record the sum and neglect the carry Step 2 – Repeat the process . Gray code b3 b2 b1 b0 1 0 1 1 +1 +0 +1 1 1 1 0 g3 g2 g1 g0
- 46. DLCA Bharati Ingale (bharatijingale@gmail.com) Binary to Gray Code conversion (XOR operation) Steps Step 1 – Record the MSB as it is Step 2 – Add MSB to the next bit, record the sum and neglect the carry Step 2 – Repeat the process . Gray code A B Y 0 0 0 0 1 1 1 0 1 1 1 0
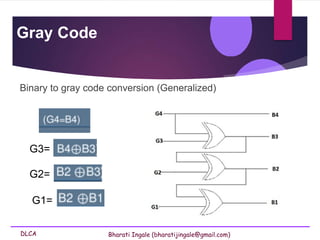
- 47. DLCA Bharati Ingale (bharatijingale@gmail.com) Binary to gray code conversion (Generalized) Gray Code G3= G2= G1=
- 48. DLCA Bharati Ingale (bharatijingale@gmail.com) Gray to Binary Code conversion (Addition) Steps Step 1 – Record the MSB as it is Step 2 – Add MSB to the next bit of Gray code, record the sum and neglect the carry Step 2 – Repeat the process . Gray code g3 g2 g1 g0 1 1 1 0 1 0 1 1 b3 b2 b1 b0 + + +
- 49. DLCA Bharati Ingale (bharatijingale@gmail.com) Gray to Binary Code conversion (XOR Operation) Steps Step 1 – Record the MSB as it is Step 2 – Add MSB to the next bit of Gray code, record the sum and neglect the carry Step 2 – Repeat the process . Gray code g3 g2 g1 g0 1 1 1 0 1 0 1 1 b3 b2 b1 b0 + + +
- 50. DLCA Bharati Ingale (bharatijingale@gmail.com) Gray –to-Binary Conversion
- 51. DLCA Bharati Ingale (bharatijingale@gmail.com) Gray –to-Binary Conversion
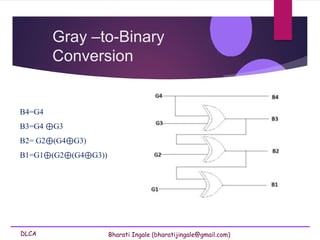
- 52. DLCA Bharati Ingale (bharatijingale@gmail.com) Gray –to-Binary Conversion B4=G4 B3=G4 ⊕G3 B2= G2⊕(G4⊕G3) B1=G1⊕(G2⊕(G4⊕G3))
- 53. DLCA Bharati Ingale (bharatijingale@gmail.com) Gray Code to Binary conversion Rules of Mod-2 Addition
- 54. DLCA Bharati Ingale (bharatijingale@gmail.com) Binary Code to Gray conversion (46)10=(?)GRAY
- 56. DLCA Bharati Ingale (bharatijingale@gmail.com) We need to digitize English text. We need to represent: – 26 uppercase, – 26 lowercase letters, – 10 numerals, – 20 punctuation characters, – 10 useful arithmetic characters, – 3 other characters (new line, tab, and backspace) ASCII code Totally 95 symbols for English
- 57. DLCA Bharati Ingale (bharatijingale@gmail.com) Assigning Symbols • To represent 95 distinct symbols, we need 7 bits – 6 bits gives only 26 = 64 symbols – 7 bits give 27 = 128 symbols • 128 symbols is ample for the 95 different characters needed for English characters • Some additional characters must also be represented
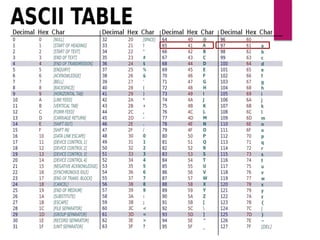
- 58. DLCA Bharati Ingale (bharatijingale@gmail.com) ASCII ASCII is an acronym for American Standard Code for Information Interchange. This is standard set of characters understood by all computers, Mostly consists of i. letters , ii. numbers and iii. few basic symbols. It is a code that uses numbers to represent characters.
- 59. DLCA Bharati Ingale (bharatijingale@gmail.com) ASCII ASCII is a widely used 7-bit (27) code Each letter is assigned a number between 0 and 127. There are 128 standard ASCII codes, each of which can be represented by a 7-digit binary number: 0000000 through 1111111. Eg: the character A is assigned the decimal number 65, while a is assigned decimal 97 as shown below in the ASCII table.
- 61. DLCA Bharati Ingale (bharatijingale@gmail.com) ASCII Advantages of a “standard”: It is relatively easy to exchange information between different programs, different operating systems, and different computers. Computer parts built by different manufacturers can be connected Programs can create data and store it so that other programs can process it later, and so forth
- 62. DLCA Bharati Ingale (bharatijingale@gmail.com) EBCDIC EBCDIC, in full extended binary-coded decimal interchange code. It was developed and used by IBM. EBCDIC) is an 8-bit binary code for numeric and alphanumeric characters. It can represent a total of 256 (28) different characters.
- 63. DLCA Bharati Ingale (bharatijingale@gmail.com) EBCDIC It is a coding representation in which symbols, letters and numbers are presented in binary language. Provide a larger set of codes thanASCII. Less common thanASCII Rarely used today It is use by IBM mainframes today
- 64. DLCA Bharati Ingale (bharatijingale@gmail.com)
- 66. DLCA Bharati Ingale (bharatijingale@gmail.com) What is an error? An error is an action which is inaccurate or incorrect. An error is a deviation from accuracy or correctness. The condition of having incorrect or false knowledge Error is a condition when the output information does not match with the input information.
- 67. DLCA Bharati Ingale (bharatijingale@gmail.com) Need of error detection and error correction When transmission of digital signals takes place between two system, the signal get contaminated due to the addition of “Noise” to it. The noise can introduce an error in the binary bits travelling from one system to the other.
- 68. DLCA Bharati Ingale (bharatijingale@gmail.com) Need of error detection and error correction That means a 0 may change to 1 or 1 may change to 0. These error can become a serious threat to the accuracy of the digital system. Therefore it is necessary to detect and correct the errors.
- 69. DLCA Bharati Ingale (bharatijingale@gmail.com) Types of Errors Single-bit errors Burst errors
- 70. DLCA Bharati Ingale (bharatijingale@gmail.com) How to detect and correct error? One or more bits are added to data for error detection /correction. These extra bits are called Parity bits. The data bits along with the parity bits form a code word. Error detection methods: Parity checking Checksum error detection Cyclic redundancy code (CRC)
- 71. DLCA Bharati Ingale (bharatijingale@gmail.com) Parity bit It is the simplest technique for detecting and correcting errors. The MSB of an 8-bits word is used as the parity bit and the remaining 7 bits are used as data or message bits. The parity of 8-bits transmitted word can be either even parity or odd parity.
- 72. DLCA Bharati Ingale (bharatijingale@gmail.com) Parity bit Even parity -- Even parity means the number of 1's in the given word including the parity bit should be even (2,4,6,....). Odd parity -- Odd parity means the number of 1's in the given word including the parity bit should be odd (1,3,5,....).
- 73. DLCA Bharati Ingale (bharatijingale@gmail.com) For even parity, this bit is set to 1 or 0 such that the no. of "1 bits" in the entire word is even. For odd parity, this bit is set to 1 or 0 such that the no. of "1 bits" in the entire word is odd. Use of Parity Bit The parity bit can be set to 0 and 1 depending on the type of the parity required.
- 74. DLCA Bharati Ingale (bharatijingale@gmail.com) How Does Error Detection Take Place? Parity checking at the receiver can detect the presence of an error if the parity of the receiver signal is different from the expected parity.
- 75. DLCA Bharati Ingale (bharatijingale@gmail.com) Hamming Code Hamming code is error detection and correction (single bit error) method. It was developed by R.W. Hamming for error correction. In this coding method, the source encodes the message by inserting redundant bits within the message. These redundant bits are extra bits that are generated and inserted at specific positions in the message . When the destination receives this message, it performs recalculations to detect errors and find the bit position that has error.
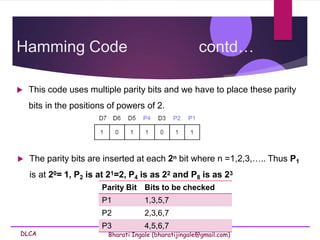
- 76. DLCA Bharati Ingale (bharatijingale@gmail.com) Hamming Code contd… This code uses multiple parity bits and we have to place these parity bits in the positions of powers of 2. The parity bits are inserted at each 2n bit where n =1,2,3,….. Thus P1 is at 20= 1, P2 is at 21=2, P4 is as 22 and P8 is as 23 Parity Bit Bits to be checked P1 1,3,5,7 P2 2,3,6,7 P3 4,5,6,7
- 77. DLCA Bharati Ingale (bharatijingale@gmail.com) Hamming Bit example Ex. A bit word 1 0 1 1 is to be transmitted. Construct the even parity seven bit Hamming code for this data. Step1: 1 0 1 1 D7 D6 D5 P4 D3 P2 P1 1 0 1 1 1 Step 2: Deciding Parity P1, P1 =1,3,5,7 =1 1 1 (Apply even parity on data) = 1 D7 D6 D5 P4 D3 P2 P1
- 78. DLCA Bharati Ingale (bharatijingale@gmail.com) Hamming Bit example contd.. Step 3: Deciding Parity P2, P2 =2,3,6,7 =1 0 1 (Apply even parity on data) = 0 1 0 1 1 1 D7 D6 D5 P4 D3 P2 P1 1 0 1 1 0 1 D7 D6 D5 P4 D3 P2 P1
- 79. DLCA Bharati Ingale (bharatijingale@gmail.com) Hamming Bit example contd.. Step 4: Deciding Parity P4, P4 =4,5,6,7 =1 0 1 (Apply even parity on data) = 0 1 0 1 1 0 1 D7 D6 D5 P4 D3 P2 P1 1 0 1 0 1 0 1 D7 D6 D5 P4 D3 P2 P1
- 80. DLCA Bharati Ingale (bharatijingale@gmail.com) Ex. 2: Encode the data bits 0 1 0 1 in seven bits even parity Hamming code. Solution 0 1 0 1 1 0 1 D7 D6 D5 P4 D3 P2 P1
- 81. DLCA Bharati Ingale (bharatijingale@gmail.com) Receiver side decoding Received Code: Solution: Step 1: Check the bits of Parity P1, P1 =1,3,5,7 =1011 (Apply even parity on data) = 1 Odd parity Therefore error exist here, put P1 = 1 in the 1’s position of error word. Error word E = = 1 0 1 1 0 1 1 D7 D6 D5 P4 D3 P2 P1 P4 P2 P1 P4 P2 1
- 82. DLCA Bharati Ingale (bharatijingale@gmail.com) Step 2: Check the bits of ParityP2, P2 =2,3,6,7 =10 0 1 (Apply even parity on data) = 0 Means no Error Step 3: Check the bits of Parity P4, P4 =4,5,6,7 =1 10 1 (Apply even parity on data) = 1 Error 1 0 1 P4 0 1
- 83. DLCA Bharati Ingale (bharatijingale@gmail.com) E = =(5) 10 1 0 1 1 0 1 1 0 1 1 Received Code: D7 D6 D5 P4 D3 P2 P1 Step 4: Correct the error Invert the incorrect bit to obtain the correct code word Correct Code word: Incorrect Bit P4 D3 P2 P1 1 0 0 1 0 1 1 D7 D6 D5
- 84. DLCA Bharati Ingale (bharatijingale@gmail.com) A seven bit Hamming code is received as 1 1 1 0 1 0 1. What is the correct code? Assume the parity to be even. P4 D3 P2 P1 D7 D6 D5 1 0 1 0 1 0 1 E= 1 1 0 = 6
- 85. DLCA Bharati Ingale (bharatijingale@gmail.com) Limitation of Hamming Code The main limitation of Hamming code is that it can detect and correct only one error
- 86. DLCA Bharati Ingale (bharatijingale@gmail.com) Codes