Lecture5 Chapter1- Binary Codes.pdf
- 1. Chapter1: Digital Systems and Binary Numbers Lecture5- Study Binary Codes Engr. Arshad Nazir, Asst Prof Dept of Electrical Engineering SEECS 1 Fall 2022
- 2. Objectives • Study Binary Codes • Perform Arithmetic operations in BCD using 10’s Complement method 2 Fall 2022
- 3. Binary Codes • Digital systems use discrete elements of information represented with binary codes (i.e., a pattern of 0’s and 1’s). The codes should be in binary because computers have circuits that represent and manipulate 0’s and 1’s. • An n-bit binary code is a group of n bits that can represent up to 2n distinct combinations of 1’s and 0’s. Each distinct combination represents a single symbol in the computer. The bit combination of an n-bit code is determined from the count in binary from 0 to 2n-1. Each element must be assigned a unique binary bit combination, and no two elements can have the same value. • Although the minimum number of bits required to code 2n distinct quantities is n, there is no maximum number of bits that can be used for a binary code. • Codes can be categorized as numeric and alphanumeric used for numbers and transmission of textual data. Fall 2022 3
- 4. BCD Code (8,4,2,1) • The most common representation for binary digits is the binary coded decimal (BCD) form which is a binary assignment of the decimal numbers. This code is the simplest, most intuitive binary code for decimal digits and uses the same weights as a binary number, but only encodes the first ten values from 0 to 9 (6 out of 16 possible combinations remains unassigned ). A number with k distinct decimal digits will require 4k bits in BCD. Each digit of a decimal value is converted to its respective binary representation. BCD number needs more bits than its equivalent binary value? • Each decimal digit in BCD code can be represented as shown in the next slide.
- 5. Binary Coded Decimal Code (BCD) Fall 2022 5
- 6. BCD Addition • BCD only represents each of the decimal digitals 0 through 9 as a single 4-bit binary value. BCD is a numeral code used in arithmetic operations in digital machines. Addition is the most important operation because the other three operations (subtraction, multiplication, and division can be accomplished using addition. Following rules apply: Add the two BCD numbers, using the rules of binary addition. If a 4-bit sum is equal to or less than 9, it is a valid BCD number. If a 4-bit sum is greater than 9, or if a carry out of the 4-bit group is generated, it is an invalid result. Add 6(0110) to the 4-bit sum in order to skip the invalid states and return the code to 8421. If a carry results when 6 is added, simply add the carry to the next significant 4-bit group. • Some BCD addition examples are: Fall 2022 6
- 7. Multi-Digit BCD Addition Fall 2022 7
- 8. BCD Arithmetic • BCD arithmetic involving negative numbers uses the 10’s complement for representing the negative numbers including the sign digit. 0 (0000) represents a positive sign and 9 (1001) represents a negative sign • As an example, imagine we want to add (+257) + (-160) = +97 Are these signed? • Note: To obtain 10’s complement of a BCD number, we first take the 9’s complement (by subtraction of each digit from 9) and then add one to least significant digit Perform subtraction (-257) - (+160) both signed and unsigned? Fall 2022 8
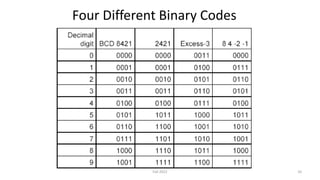
- 9. Other Decimal Codes • There are various other decimal codes that can be used: BCD (8, 4, 2, 1) 2, 4, 2, 1 Excess-3 code. (adds binary 0011 to the BCD code) 8, 4, -2, -1 Gray Code ASCII Character Code Error-Detecting Code • Each bit has a "weight" associated with it and you can compute the decimal value by adding the weights where a 1 exists in the code- word. Fall 2022 9
- 10. Four Different Binary Codes Fall 2022 10
- 11. Gray Code • The Gray (reflected) code is named after Frank Gray who patented it for shaft encoders in 1953. It is un-weighted and non-arithmetic code; that is, there are no specific weights assigned to the bit positions • Some of the uses of Gray code are:- Conversion of physical variables like position or voltage that have a continuous range of values to a digital representation. A different use of Gray codes appears in low-power CMOS logic circuits that count up or down. • Gray code is cyclic code i.e any n-bit code can be generated form n-1 bit code by taking reflection along the mirror and padding the two halves with 0’s and 1’s respectively. • The advantage of Gray code over straight binary number sequence is that only one bit in the code group changes when going from one number to the next (unit distance code). Fall 2022 11
- 12. Gray Code Cont… • This property is important in many applications, such as optical shaft angle encoders, where error susceptibility increases with the number of bit changes between adjacent numbers in a sequence. • Optical shaft encoder is a disc attached to rotating shaft to measure its rotational position. The disc contains areas that are clear for binary 1 and opaque for binary 0. An illumination source is placed on one side of the disc, and optical sensors, one for each of the bits to be encoded are placed on the other side of the disc. When a clear region lies between the source and a sensor, the sensor responds to the light with a binary 1 output. When opaque region lies between the source and the sensor, the sensor responds to the dark with a binary 0. • The optical shaft encoder using 3-Bit Gray code for positions 0 through 7 is shown in the next slide. Fall 2022 12
- 13. Fall 2022 13
- 14. Gray Code Vs Binary Code • Compare the number of bits changing when going from one number to the next for a three-bit Binary and Gray Code: In Gray code it is always 1-bit change (unit- distance code). Can you guess the applications where this important property can be used in digital applications? Fall 2022 14
- 15. Gray Code Cont… Fall 2022 15
- 16. Conversion from Binary to Gray Code • Binary to Gray code Conversion: The following rules apply: The most significant bit (left-most) in the Gray code is the same as the corresponding MSB in the binary number. Going from left to right, add each adjacent pair of binary code bits to get the next Gray code bit and discard carries. Which addition? For example, the conversion of binary number 10110 to Gray Code is as follows The Gray Code is 11101. Fall 2022 16
- 17. Conversion from Gray to Binary Code • Gray to Binary code Conversion: The following rules apply: The most significant bit (left-most) in the Binary code is the same as the corresponding MSB in the Gray code. Add each Binary code bit generated to the Gray code bit in the next adjacent position and discard carries. For example, the conversion of Gray number 11011 to Binary code is as follows The binary number is 10010. Fall 2022 17
- 19. Your Turn • Write 196510 in the following codes: 8, 4, 2, 1= 8, 4, -2, -1= 6, 3, 1, 1= Excess-3= Gray= • Which of these codes are self-complementing? Fall 2022 19