Compact binary-tree-representation-of-logic-function-with-enhanced-throughput-

World Academy of Science, Engineering and Technology
International Journal of Computer, Information Science and Engineering Vol:1 No:4, 2007

Compact Binary Tree Representation of Logic
Function with Enhanced Throughput
Padmanabhan Balasubramanian, Cemal Ardil

International Science Index 4, 2007 waset.org/publications/6263

Abstract—An effective approach for realizing the binary tree
structure, representing a combinational logic functionality with
enhanced throughput, is discussed in this paper. The optimization in
maximum operating frequency was achieved through delay
minimization, which in turn was possible by means of reducing the
depth of the binary network. The proposed synthesis methodology
has been validated by experimentation with FPGA as the target
technology. Though our proposal is technology independent, yet the
heuristic enables better optimization in throughput even after
technology mapping for such Boolean functionality; whose reduced
CNF form is associated with a lesser literal cost than its reduced
DNF form at the Boolean equation level. For cases otherwise, our
method converges to similar results as that of [12]. The practical
results obtained for a variety of case studies demonstrate an
improvement in the maximum throughput rate for Spartan IIE
(XC2S50E-7FT256) and Spartan 3 (XC3S50-4PQ144) FPGA logic
families by 10.49% and 13.68% respectively. With respect to the
LUTs and IOBUFs required for physical implementation of the
requisite non-regenerative logic functionality, the proposed method
enabled savings to the tune of 44.35% and 44.67% respectively, over
the existing efficient method available in literature [12].

Keywords—Binary logic tree, FPGA based design, Boolean
function, Throughput rate, CNF, DNF.
I. INTRODUCTION

T

issue of performance enhancement has been a subject
matter of much research [1] [2] [3] [4] [5]. Also the
relevance of FPGAs based on LUTs in the last decade has
fostered numerous efforts in finding effective methods to
minimize and decompose functions. This paper deals with a
novel technology-independent synthesis methodology to
realize compact and throughput enhanced binary tree
structures for combinational logic circuits, by way of reducing
the logic depth. A number of techniques mentioned in [7] [8]
[9] are technology-independent and aim at reducing the logic
depth of the binary tree representing a Boolean network by
restructuring. Directed acyclic directed graphs (DAG) are
generally used to effectively represent single output
combinational logic circuit functionality. A rooted DAG may
be unfolded to a tree in such a way that no multiple-fanout
nodes exist, except for the primary circuit inputs. Each
internal node is labeled with a logical operator, AND and/or
HE

Padmanabhan Balasubramanian is with the School of Computer Science,
The University of Manchester, Manchester, MAN M13 9PL UK (phone: +44161-275 6294; e-mail: spbalan04@gmail.com, padmanab@cs.man.ac.uk).
Cemal Ardil is with the National Academy of Aviation, Baku,
Azerbaijan (e-mail: cemalardil@gmail.com).

OR, although other operators are also used depending upon
the functionality. In this work, we are primarily concerned
with function representations employing just these two types
of Boolean operations. A labeled edge (dot appearing on an
edge) in a DAG or a binary tree would correspond to a logical
inversion or negation operation. Let us have a reasonable and
valid assumption that all DAGs are reduced and that
isomorphism is not exhibited in the sub-DAGs.
Tree-height reduction was indeed proposed [6] in the scope
of compiler optimization, for code generation in
multiprocessor systems. Given the underlying inherent
complexity of the problem, timing optimization is sought
after, after the size of the Boolean network representing the
circuit has been reduced. Even extraction of kernels, that can
be shared, may lead to an increase in the depth of the network
as an associated effect. This makes it clear that sharing logic is
not always deemed to be a good approach, when considering
the issue of timing optimization. A technique that performs
logic decomposition during technology mapping has been
proposed in [10] [11]. However, the accuracy of this approach
is traded off for a higher computational cost. A recent activity
[12] addresses the issue of delay improvement through
functional decomposition. It actually builds on logic bidecomposition of Boolean functions [13] [14] and also uses
weak algebraic factorization operations. It implicitly relies
upon OR disjunction for functional bi-decomposition. Then it
combines this strategy with tree-height reduction of resulting
Boolean expressions. Though it leads to enhancement in
performance, vis-à-vis achieving logic depth reduction, the
quasi-algebraic decomposition was normally performed on the
minimized disjunctive normal form (DNF) [15], by iteratively
applying a combination of associative, distributive and
commutative (ACD) laws.
The remaining portion of this paper is organized as follows.
In section 2, we introduce a novel terminology, namely the
description set of a Boolean term and give its definition.
Section 3 elucidates the proposed method by means of an
illustrative example and compares it with the solution
obtained using the ACD based algorithm [12] at both the
technology-independent and technology-dependent phases.
Section 4 depicts the simulation results obtained for several
Boolean functions. A comparison of the methods in terms of
the maximum operating frequency achievable for the designs
is given in this section. The resource utilization summary is
also listed in this section. Finally, we make the concluding
remarks in the next section.

514


II. DESCRIPTION SET OF A BOOLEAN TERM
A new terminology is proposed, namely the description set
of a Boolean term (sum term or product term). The description
set of a sum term [product term], shall be represented by the
notation D(Si) [D(Pi)].
D(Si) specifies the set of all literals in their actual form, that
the particular sum term Si is dependent upon for its evaluation
to a logic value of ‘0’ and D(Pi) indicates the set of all literals
in their respective form, that a product term Pi depends upon
for its evaluation to a logic value of ‘1’.
For e.g. let a sum-of-disjoint products (SoDP) function be,
Z = AC’DE + B’FG’, where there are two disjoint product
terms; P1 = AC’DE and P2 = B’FG’. Hence D(P1) = {A,
C’,D,E} and D(P2) = {B’,F,G’}.
The description set for a Boolean function would then be
the union of the description sets of all its individual terms. For
the above example, it is given by, D(Z) = D(P1) ∪ D(P2).


III. ILLUSTRATION OF PROPOSED HEURISTIC
Let us take an arbitrary logic function, F to describe the
effectiveness of our proposal. Let F(Q,R,S,T,U,V,W) be
described by the following minimized expression,
F = TRU+TRV+ST’W+SU+SV+QT’W+QU+QV

(1)

Using the ACD based heuristic as described in [12], two
logically equivalent and irredundant reduced expressions are
obtained as follows,
F = (TR)·(U+V)+(Q+S)·(T’W+U+V)

(2)

F = (TR+Q+S)·(U+V)+(T’W)·(Q+S)

be combined with just one another different product term at
the end.
As a further generalization, it can be intuitively observed
that if the total number of distinct product terms in the reduced
two-level representation of a logic function is ‘n’; whether ‘n’
is ‘odd’ or ‘even’; the total number of set union operations
required to be performed would be O[n(n-1)/2].
Now we make a decision with regard to grouping those
terms, whose degree of literal matching is the highest, as
determined by the cardinality of the union of the description
set of all possible combinations of two unique Boolean terms.
Therefore for (4), we find that S1 and S2 can be combined
using the distributive law; similarly S3 and S4 are candidates to
be combined using the same axiom. After applying the D rule
for the appropriate terms of (4), which could be grouped, we
get the following reduced expression,
F = (TR+S+Q)·(T’W+U+V)

(5)

Comparing (2) [also (3)] and (5), we find that there is a
savings of 20% in terms of literal count. After representing the
tree structures for (2) and (5) in accordance with the DAG
specification and with sharing of nodes permitted, we observe
that there is a reduction in the number of operators and logic
depth by 12.5% and 25%, for the latter in comparison with the
former. Without node sharing, and for the worst case
realization, the respective savings for the proposed method
would be 22.22% and 40% respectively.
The binary tree representation with node sharing for (1),
given by (2), is shown in fig. 1. The symbols
and
denote Boolean AND and Boolean OR operators respectively
and these are referred to as atomic operators (AO) [16].

(3)

Both the above Boolean equations (2) and (3) have the
same input literal cost. The reduced conjunctive normal form
(CNF) equivalent for (1) is given by,
F = (T+S+Q)·(R+S+Q)·(T’+U+V)·(W+U+V)

(4)

For (4), we could write D(S1) = {T,S,Q}, D(S2) = {R,S,Q},
D(S3) = {T’,U,V} and D(S4) = {W,U,V}. We perform the
union of the description set of a sum term with all other sum
terms of (4) and we get the following: D(S1) ∪ D{S2}= {S,Q},
D(S1) ∪ D(S3) = { }, D(S1) ∪ D(S4) = { }, D(S2) ∪ D(S3) =
{ }, D(S2) ∪ D(S4) = { } and D(S3) ∪ D(S4) = {U,V}. We
now enumerate the cardinality of the above union and thereby
obtain | D(S1) ∪ D(S2) | = 2, | D(S1) ∪ D(S3) | = 0, | D(S1) ∪
D(S4) | = 0, | D(S2) ∪ D(S3) | = 0, | D(S2) ∪ D(S4) | = 0 and
| D(S3) ∪ D(S4) | = 2.
In general, for a function whose minimized two-level CNF
expression contains ‘k’ product terms, the first product term,
say, P1 could be combined with (k-1) different product terms,
the second product term, P2 could be combined with (k-2)
distinct product terms till the (k-1)th product term, which could

Fig. 1 Binary tree representation for (1) based on ACD heuristic

Theoretically speaking, the maximum operating frequency
for fig. 1, given as a reciprocal of the longest path delay or
critical path delay is given by,

515


1
t AN D + 3 tO R

f m ax =

=

1
2 t AN D + 2 tO R

(6)

For representation without duplication of nodes and with no
node sharing, the upper bound on the maximum frequency is,
f

m

a x

=

1
2 t

A

N

D

+

(7)
3 t

O

R


Fig. 1 is characterized by a maximum logic depth of 4
(specified by the number of nodes in the longest path from
any of the primary inputs to a primary output for a MISO
function) and maximum operating frequencies of 89.847 MHz
and 101.626 MHz for technology mapping with Spartan IIE
(XC2S50E-7FT256) and Spartan 3 (XC3S50-4PQ144) FPGA
logic families as targets. The binary tree structure consumed 5
basic logic elements (LUTs of FPGA) and 16 input-output
buffers for physical realization.
The binary logic tree representation corresponding to (5) is
depicted by fig. 2.

Fig. 2 Binary tree representation for (1) based on proposed method

As seen above, this tree representation requires less number
of nodes than fig. 1 and the theoretical upper bound on the
maximum throughput rate is given by the expression,
fm

ax

=

t

A N D

1
+ 2 tO R

=

1
2 t AN D + tO R

(8)

The maximum logic depth of the tree structure is 3 and the
highest operating frequency for Spartan IIE and Spartan 3
FPGA logic families is found to be 99.009 MHz and 118.203
MHz respectively. Also the structural representation required
3 basic logic elements and 9 input-output buffers for
implementation with the above technology targets.
For this particular case study, we find that the throughput
rate is increased by 10.19% and 16.31% for the FPGA target
families in the above order. With respect to the basic logic
elements and input-output buffers needed for technology

mapping, corresponding savings of 40% and 43.75% has
resulted for the proposed procedure over that of [12].
IV. SIMULATION MECHANISM AND PRACTICAL RESULTS
Various combinational logic functions in canonical form of
various types were considered to substantiate the theoretical
claims by validating with experimental results. The
functionalities in PLA format were first minimized using a
commercial industry standard two-level logic minimizer, such
as ESPRESSO [17] and they are listed in Table 5 (made
available as an appendix).
The binary tree structures highlighting the BDAG
representation for the combinational circuits were realized
using the ACD rules based methodology described in [12].
VHDL coding was done for all the functions using structural
modeling style with gate-level primitives strictly conforming
to the binary DAG specification. The detailed design summary
and timing reports were obtained after post place and route
stage. The maximum operating frequency of the different
designs was then determined as a reciprocal of the maximum
combinational logic path delay.
The reduced conjunctive normal forms for the functions can
be obtained by two methods; either by running a direct sumof-products to product-of-sums subroutine or by considering
the complementary phase of the function and a
straightforward conversion to reduced product-of-sums
expression could be done. Infact, a high level language
implementation of the modified Quine-McCluskey’s method
for two-level logic minimization [18] can also be used in this
regard. Next, the description set for the different product
terms corresponding to each and every function was obtained
as per the definition given in section 2. Set union operations
were then performed on the different sets and the candidates
suitable for grouping were found according to the method
explained in section 3. Distributive axiom was applied, so that
the function now tends to comprise reduced, compact and
read-once functionality for the sub-functions, though not in
the original function. Then the tree representation was created
using the basic atomic operators and VHDL coding was done
using a similar modeling style. The design summary and
timing reports were obtained after the placement and routing
phase.
The simulations were all performed with Xilinx project
navigator suite targeting Spartan IIE and Spartan 3 FPGA
boards. The Spartan FPGA logic families are ideally suited for
gate-level designs [19].
Table 1 gives a description of the comparison between the
two schemes in terms of the logical operators required and
literal count. Table 2 shows the maximum throughput rate for
the synthesized tree representations corresponding to the
desired Boolean functionality, based on the two different
methods. Table 3 gives the amount of basic logic elements
utilized (BEL) for the different techniques and Table 4 gives
an account of the input-output buffers (IOBUF) utilized for
the two schemes.

516



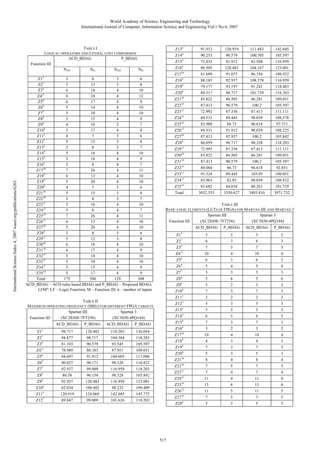
TABLE I
LOGICAL OPERATORS AND LITERAL COST COMPARISON
ACD_BDAG
P_BDAG
Function ID
NIL
NAO
NIL
NAO
Z15
3
8
3
6
Z27
5
12
3
8
Z39
6
18
4
10
Z411
6
24
4
12
Z58
6
17
4
9
Z69
5
14
4
10
Z77
5
10
4
10
Z88
5
15
4
9
Z96
4
10
3
7
Z108
5
17
4
9
Z115
4
7
3
6
Z127
5
15
3
8
Z136
3
8
3
7
Z149
5
16
4
10
Z158
5
18
4
9
Z166
5
8
4
7
Z1710
7
26
4
11
Z189
6
13
4
10
Z199
5
20
4
10
Z208
4
7
3
6
Z2110
5
15
3
8
Z2210
3
8
3
7
Z2311
5
16
4
10
Z2412
5
8
4
7
Z2516
7
26
4
11
Z2612
6
13
4
10
Z2710
5
20
4
10
Z288
3
8
3
6
Z2911
5
12
3
8
Z3010
6
18
4
10
Z3110
6
17
4
9
Z3215
5
14
4
10
Z3311
5
10
4
10
Z3411
5
15
4
9
Z3514
5
17
4
9
Total
175
500
129
308
ACD_BDAG – ACD rules based BDAG and P_BDAG – Proposed BDAG;
LFMn: LF – Logic Function, M – Function ID, n – number of inputs

Z136
Z149
Z158
Z166
Z1710
Z189
Z199
Z208
Z2110
Z2210
Z2311
Z2412
Z2516
Z2612
Z2710
Z288
Z2911
Z3010
Z3110
Z3215
Z3311
Z3411
Z3514
Total

ACD_BDAG

P_BDAG

ACD_BDAG

120.482
98.717
90.579
88.183
91.912
90.171
99.009
96.154
120.482
100.402
124.069
99.009

118.203
104.384
93.545
87.951
104.603
98.328
116.959
98.328
116.959
98.232
142.045
101.626

111.483
100.705
82.508
104.167
86.356
108.578
91.241
101.729
86.281
100.2
87.413
98.039
96.618
98.039
100.2
98.328
87.413
86.281
100.2
96.618
103.95
98.039
88.261
3493.810

142.045
105.597
116.959
123.001
108.932
116.959
118.483
118.203
109.051
105.597
111.111
108.578
97.371
108.225
103.842
118.203
111.111
109.051
105.597
92.851
109.051
108.932
101.729
3971.732

ACD_BDAG
Z15
Z27
Z39
Z411
Z58
Z69
Z77
Z88
Z96
Z108
Z115
Z127
Z136
Z149
Z158
Z166
Z1710
Z189
Z199
Z208
Z2110
Z2210
Z2311
Z2412
Z2516
Z2612
Z2710
Z288

P_BDAG

98.717
94.877
81.103
78.989
94.697
90.827
92.937
86.58
92.937
82.034
120.919
89.847

120.919
90.579
91.912
120.482
91.075
92.937
93.197
98.717
86.505
90.579
87.336
89.445
86.73
91.912
92.937
98.717
87.336
86.505
90.579
86.73
89.445
82.85
84.034
3350.627

TABLE III
BASIC LOGIC ELEMENTS (LUTS OF FPGA) FOR SPARTAN IIE AND SPARTAN 3
Spartan IIE
Spartan 3
(XC2S50E-7FT256)
(XC3S50-4PQ144)
Function ID

TABLE II
MAXIMUM OPERATING FREQUENCY (MHZ) FOR DIFFERENT FPGA TARGETS
Spartan IIE
Spartan 3
(XC2S50E-7FT256)
(XC3S50-4PQ144)
Function ID
Z15
Z27
Z39
Z411
Z58
Z69
Z77
Z88
Z96
Z108
Z115
Z127

91.912
90.253
72.833
86.505
81.699
88.183
79.177
84.317
83.822
87.413
72.992
84.531
82.988
84.531
87.413
86.059
72.993
83.822
87.413
80.064
91.324
83.963
83.682
3032.353

136.054
118.203
105.597
109.051
117.096
116.822
118.203
103.842
123.001
109.409
145.772
118.203

517

P_BDAG

ACD_BDAG

P_BDAG

3
6
7
10
6
5
3
5
3
7
2
5
3
6
7
3
10
4
7
5
8
7
7
11
13
11
7
5

2
3
5
4
3
4
3
6
2
3
2
3
2
5
3
2
4
3
3
3
4
5
4
4
6
5
5
3

3
6
7
10
6
5
3
5
3
7
2
5
3
6
7
3
10
4
7
5
8
7
7
11
13
11
7
5

2
3
5
4
3
4
3
6
2
3
2
3
2
5
3
2
4
3
3
3
4
5
4
4
6
5
5
3


Z2911
Z3010
Z3110
Z3215
Z3311
Z3411
Z3514
Total

7
8
7
13
8
11
9
239

4
4
5
6
4
4
5
133

7
8
7
13
8
11
9
239

4
4
5
6
4
4
5
133

TABLE IV
INPUT-OUTPUT BUFFERS REQUIRED FOR THE TWO SCHEMES
Spartan IIE
Spartan 3
(XC2S50E-7FT256)
(XC3S50-4PQ144)
Function ID
ACD_BDAG P_BDAG ACD_BDAG P_BDAG
9
15
19

11

19

11

Z411


Z15
Z27
Z39

25

13

25

13

Z58
Z69
Z77
Z88
Z96
Z108
Z115
Z127
Z136
Z149
Z158
Z166
Z1710
Z189
Z199
Z208
Z2110
Z2210
Z2311
Z2412
Z2516
Z2612
Z2710
Z288
Z2911
Z3010
Z3110
Z3215
Z3311
Z3411
Z3514
Total

18
15
11
16
11
18
8
16
9
17
19
9
27
14
21
16
24
18
22
34
38
34
18
16
22
24
18
37
19
33
24
694

10
11
9
10
8
10
7
9
8
11
10
8
12
11
11
9
11
11
12
13
17
13
11
9
12
11
11
17
13
13
16
384

18
15
11
16
11
18
8
16
9
17
19
9
27
14
21
16
24
18
22
34
38
34
18
16
22
24
18
37
19
33
24
694

10
11
9
10
8
10
7
9
8
11
10
8
12
11
11
9
11
11
12
13
17
13
11
9
12
11
11
17
13
13
16
384

7
9

9
15

7
9

possible by way of reducing the logic depth in a binary logic
tree representation is discussed in this paper. A fair degree of
correlation is observed between the depth of the Boolean
network at the technology-independent stage represented by a
tree and the practical critical delay parameter obtained
experimentally; however, it turns out to be contrary in some
cases after the technology-mapping phase. The approach
seems to yield optimization in the throughput rate for a wide
variety of problems, which tend to have compact conjunctive
normal forms in comparison with disjunctive normal forms,
with the degree of compactness measured in terms of literal
count at the Boolean equation level.
The effectiveness of our contribution is evident from
improved results of reachability along the computationally
intensive path. Through extensive simulation studies, we infer
that the proposed methodology is promising, as it enables
higher operating frequency and less resource utilization
(FPGA resources) in parallel for significant number of case
studies. We have successfully addressed the issues of delay
improvement and area reduction, highlighted in [12], by
exploring the available design space and achieved
enhancement in performance.
Before technology mapping, with respect to the reduced
expressions governing the actual logic description, we find
that in terms of the atomic operators and input literal count,
the proposed procedure enabled savings of 26.29% and 38.4%
respectively. From the experimental results obtained, we find
that the average improvement in performance (measured in
terms of maximum operating frequency) has been 10.49% and
13.68% for Spartan IIE and Spartan 3 FPGA logic family
targets respectively. The corresponding average decrease in
LUTs for the logic families stated in the above order has been
the same and is around 44.35%. Based on the number of
input-output buffers required for physical realization of the
desired functionality, the proposed method effected mean
savings to the tune of 44.67% for both the logic families.
For functions with DNF forms more compact than its CNF
forms, the proposed heuristic returns the same results as that
of [12], while for the contrary, the approach enables decent
enhancement in throughput rate, whilst ensuring minimum
resource utilization. The approach is pragmatic and results in
tree representations for non-regenerative logic functions,
which promise improved performance, evident from several
problem cases considered in this work.
ACKNOWLEDGMENT
The authors would like to thank Mrs. Prathibha for her
assistance in this work.
REFERENCES

V. CONCLUSION
This paper deals with a technology-independent synthesis
methodology for combinational logic functionality that
typically precedes the technology-mapping phase. An
effective technique to address the important issue of
throughput enhancement via, timing optimization, made

[1]
[2]
[3]

518

R. Ashenhurst, “The decomposition of switching functions,” Proc. of
International Symposium. on Switching Theory, 1959, pp. 74-116.
J. Baer, and D. Bovet, “Compilation of arithmetic expressions for
parallel computations,” Proc. of IFIP Congress, 1968, pp. 340-346.
J. Beatty, “An axiomatic approach to code optimization for expressions,”
Journal of ACM, vol. 19(4), 1972, pp. 613-640.


[4]

[5]

[6]
[7]

[8]

[9]

[10]

[11]


[12]

[13]

[14]

[15]
[16]
[17]

[18]

[19]

R. Brayton, and C. McMullen, “The decomposition and factorization of
Boolean expressions,” Proc. of International Symposium on Circuits and
Systems, 1982, pp. 49-54.
J. Vasudevamurthy, and J. Rajski, “A method for concurrent
decomposition and factorization of Boolean expressions,” Proc. of
International Conf. on Computed-Aided Design, 1990, pp. 510-513.
D. Kuck, The Structure of Computers and Computation, Wiley, 1978.
K. Singh, A. Wang, R. Brayton, and A. Sangiovanni-Vincentelli,
“Timing optimization of combinational logic,” Proc. of IEEE/ACM
International Conf. on Computer-Aided Design, 1988, pp. 282-285.
K. Chen, and S. Muroga, “Timing optimization for multi-level
combinational circuits,” Proc. of ACM/IEEE Design Automation Conf.,
1990, pp. 339–344.
H.Touati, H.Savoj, and R.Brayton, “Delay optimization of
combinational circuits by clustering and partial collapsing,” Proc. of
IEEE/ACM International Conf. on Computer-Aided Design, 1991, pp.
188-191.
Eric Lehman, and Yosinori Watanabe, “Logic Decomposition during
Technology Mapping,” Proc. of IEEE/ACM International Conf. on
Computer-Aided Design, 1995, pp. 264-271.
E. Lehman, Y. Watanabe, J. Grodstein, and H. Harkness, “Logic
decomposition during technology mapping,” IEEE Transactions on CAD
of Integrated Circuits and Systems, vol. 16(8), August 1997, pp. 813834.
J. Cortadella, “Timing-Driven Logic Bi-Decomposition,” IEEE
Transactions on CAD of Integrated Circuits and Systems, vol. 22(6),
June 2003, pp. 675–685.
S. Yamashita, H. Sawada, and A. Nagoya, “New methods to find
optimal nondisjoint bi-decompositions,” Proc. of ACM/IEEE Design
Automation Conf., 1998, pp. 59-68.
A. Mishchenko, B. Steinbach, and M. Perkowski, “An algorithm for bidecomposition of logic functions,” Proc. of ACM/IEEE Design
Automation Conf., 2001, pp. 282-285.
Zvi Kohavi, Switching and Finite Automata Theory, McGraw Hill, 1999.
Srinivas Devadas, Abhijit Ghosh, and Kurt Kuetzer, Logic Synthesis
McGraw-Hill series on Computer Engineering, 1994.
P.C. McGeer, J.V. Sanghavi, R.K. Brayton, and A.L. SangiovanniVincentelli, “ESPRESSO-SIGNATURE: a new exact minimizer for
logic functions,” IEEE Transactions on VLSI Systems, vol. 1(4),
December 1993, pp. 432-440.
S.P. Tomaszewski, I.U. Celik, and G.E. Antoniou, “www based Boolean
function minimization,” International Journal of Applied Mathematics
and Computer Science, vol. 13(4), 2003, pp. 577-583.
Available: http://www.xilinx.com/support/mysupport.htm#Spartan-3

519


APPENDIX

Function ID

TABLE V
LOGIC FUNCTION SPECIFICATION
Minimized two-level logic obtained using ESPRESSO [17]

Z15

agb+agc+abf+fc

Z2

7

afe+afd+afg+aec+cd+cg+abe+bd+bg

Z39

dbfcg+dbfgh+dbfi+dceg+eh+ei+adcg+ah+ai

Z411

mnqst+mnqu+mnqv+mnqw+msto+uo+vo+wo+mstp+up+vp+wp+mstr+ur+vr+wr

Z58

ijn+ijo+ijp+kin+ko+kp+inl+ol+pl+min+mo+mp

Z69

pqrsuvw+pqrsx+puvwt+xt

Z77

mnpq+mnpr+mnqo+ro

Z8

8

qrwx+qru+qrv+qwxs+su+sv+qwxt+tu+tv

Z96

bgc+bgd+bge+abc+ad+ae

Z108

abe+abf+abg+abh+aec+fc+gc+hc+aed+fd+gd+hd

Z115

stw+s’vu+uw
tru+trv+t’ws+us+vs+t’wq+qu+qv (FOR ILLUSTRATION)

Z136


Z127

pmr+p’qn+nr+p’qo+or

Z149

abch+abci+a’fgh+dh+di+a’fge+eh+ei

Z15

8

pmx+pmy+qp’v+qx+qy+p’vw+wx+wy+p’vu+ux+uy

Z166

mnr+m’pqo+or

Z1710

mnv+mnw+mnx+m’uq+vq+wq+xq+m’ur+vr+wr+xr+m’us+vs+ws+xs+m’ut+vt+wt+xt

Z189

abci+a’ghd+di+a’ghe+ei+a’ghf+fi

Z199

wxn+wxo+wxp+wxq+w’my+ny+oy+py+qy+w’mz+nz+oz+pz+qz

Z208

pqrsm+pqrsn+pqrso+pqrsp+p’xyzt+mt+nt+ot+pt+p’xyzu+mu+nu+ou+pu+

Z2110

defgl+defgk+d’onmh+lh+kh+d’onmi+li+ki

Z2210

ijp+ijq+ijr+ijs+i’ok+pk+qk+rk+sk+i’ol+pl+ql+rl+sl+i’om+pm+qm+rm+sm+

Z2311

cdefgn+cdefgo+c’jklmh+nh+oh+c’jklmi+ni+oi

Z2412

a’be’f+a’bg+a’bh+ce’f+cg+ch+de’f+dg+dh

p’xyzv+ mv+nv+ov+pv+p’xyzw+mw+nw+ow+pw

i’on+pn+qn+rn+sn

Z2516

i’jkn’op+i’jkq+i’jkr+n’opl+ql+rl+n’opm+ qm+rm

Z2612

p’qrv’wx+p’qry+p’qrz+v’wxs+sy+sz+v’wxt+ty+tz+uv’wx+uy+uz

Z2710

a’bcdg’hij+a’bcdk+a’bcdl+g’hije+ke+le+g’hijf+kf+lf

Z288

r’sx’y+r’sz+r’sm+r’sn+r’so+x’yt+zt+mt+nt+ot+x’yu+zu+mu+nu+ou+x’yv+

Z2911

c’defgjklmn+c’defgo+c’defgp+j’klmnh+ho+hp+j’klmni+io+ip

Z3010

p’qrsx’yzm+p’qrsn+p’qrso+p’qrsk+p’qrsl+x’yzmt+nt+ot+kt+lt+x’yzmu+nu+

Z3110

a’bcf’gh+a’bci+a’bcj+f’ghd+id+jd+f’ghe+ie+je

Z3215

g’hk’l+g’hm+g’hn+k’li+mi+ni+k’lj+mj+nj

Z3311

o’pqu’vw+o’pqx+o’pqy+u’vwr+rx+ry+u’vws+xs+ys+u’wvt+xt+yt

Z3411

e’fj’k+e’fl+e’fm+e’fn+j’kg+lg+mg+ng+j’kh+lh+mh+nh+j’ki+li+mi+ni

Z3514

q’rsv’wx+q’rsy+q’rsz+v’wxt+yt+zt+v’wxu+uy+uz
ZXn; X – Function ID, n – Number of primary inputs

zv+mv+nv+ov+x’yw+zw+mw+nw+ow

ou+ku+lu+x’yzmv+nv+ov+kv+lv+x’yzmw+nw+ow+kw+lw

520

Compact binary-tree-representation-of-logic-function-with-enhanced-throughput-

More Related Content

What's hot (19)

Viewers also liked (6)

Similar to Compact binary-tree-representation-of-logic-function-with-enhanced-throughput- (20)

More from Cemal Ardil (20)

Recently uploaded (20)

Compact binary-tree-representation-of-logic-function-with-enhanced-throughput-