COORDINATE GEOMETRY II

COORDINATE GEOMETRY II
CONIC SECTIONS
Definition
Conic sections or conics are the sections whose ratios of the distance of the variables point from
the fixed point to the distance, or the variable point from the fixed line is constant
TYPES OF CONIC SECTION
There are i) Parabola
ii) Ellipse
iii) Hyperbola

IMPORTANT TERMS USED IN CONIC SECTION
I. FOCUS
This is the fixed point of the conic section.
For parabola
S → focus
For ellipse

S and S’ are the foci of an ellipse
II. DIRECTRIX
This is the straight line whose distance from the focus is fixed.
For parabola

For ellipse
III. ECCENTRICITY (e)
This is the amount ratio of the distance of the variable point from the focus to the distance
of the variables point from the directrix.
For Parabola

For ellipse
IV. AXIS OF THE CONIC
This is the straight line which cuts the conic or conic section symmetrically into two equal
parts.

For parabola
X-axis is the point of the conic i.e. parabola
Also
Y-axis is the axis of the conic

FOR ELLIPSE
AB – is the axis (major axis) of the Conic i.e. (ellipse)
CD – is the axis (minor axis) the Conic i.e. (ellipse)
→An ellipse has Two axes is major and minor axes
V FOCAL CHORD
This is the chord passing through the focus of the conic section.

For parabola
For ellipse
VI LATUS RECTRUM
This is the focal cord which is perpendicular to the axis of the conic section.
For parabola

For Ellipse
Note:
Latus rectum is always parallel to the directrix
VII. VERTEX

This is the turning point of the conic section.
For parabola
0 – is the vertex
For ellipse
Where V and V1 is the vertex of an ellipse
PARABOLA

This is the conic section whose eccentricity, e is one i.e. e = 1
For parabola
SP = MP
EQUATIONS OF THE PARABOLA
These are;
a) Standard equation
b) General equations
A. STANDARD EQUATION OF THE PARABOLA
1st case: Along the x – axis
· Consider the parabola whose focus is S(a, 0) and directrix x = -a

Squaring both sides
Is the standard equation of the parabola
PROPERTIES
i) The parabola lies along x – axis
ii) Focus, s (a, o)

iii) Directrix x = -a
iv) Vertex (0, 0) origin
Note:
PROPERTIES
1) The parabola lies along x – axis
2) Focus s (-a, o)
3) Directrix x = a
4) Vertex (o, o) origin
2nd case: along y – axis
Consider the parabola when focus is s (o, a) and directrix y = -a

· Is the standard equation of the parabola along y – axis
PROPERTIES
i) The parabola lies along y – axis
ii) The focus s (o, a)

iii) Directrix y = -a
iv) Vertex (o, o) origin
Note;
Hence, x2 = -4ay
PROPERTIES
i) The parabola lies along y – axis
ii) Focus s (o, -a)
iii) Directrix y = a
iv) Vertex (o, o)

GENERAL EQUATION OF THE PARABOLA
· Consider the parabola whose focus is s (u, v) and directrix ax + by + c = 0
Is the general equation of the parabola
Where;

S (u, v) – is the focus
Examples:
1. Find the focus and directrix of the parabola y2 = 8x
Solution
Given y2 = 8x
Comparing from
2. Find the focus and the directrix of the parabola
y2 = -2x
Solution
Compare with

3. Find the focus and directrix of x2 = 4y
Solution
4. Given the parabola x2 =
a) Find i) focus
ii) Directrix

iii) Vertex
b) Sketch the curve
Solution
i) Focus =
ii) Directrix, y = a
iii) Vertex
b) Curve sketching

5. Find the equation of the parabola whose focus is (3, 0) and directrix
X = -3
Solution
Given focus (3, 0)
Directrix, x = -3
(3, 0) = (a, 0)
From
y2 = 4 (3)x

6. Find the equation of the parabola whose directrix, y =
Solution
Given directrix, y =
Comparing with
7. Find the equation of the parabola whose focus is (2, 0) and directrix, y = - 2.
Solution
Focus = (2, 0)
Directrix y = -2

8. Find the equation of the parabola whose focus is (-1, 1) and directrix x = y
Solution
Given: focus = (-1, 1)
Directrix x = y

PARAMETRIC EQUATION OF THE PARABOLA
The parametric equation of the parabola are given
X = at2 and y = 2at
Where;
t – is a parameter
TANGENT TO THE PARABOLA
Tangent to the parabola, is the straight line which touches it at only one point.
Where, p – is the point of tangent or contact
CONDITIONS FOR TANGENT TO THE PARABOLA
a) Consider a line y = mx + c is the tangent to the parabola y2 = 4ax2. Hence the condition for
tangency is obtained is as follows;

i.e.
b) Consider the line ax + by + c = is a tangent to the parabola y2 = 4ax Hence, the condition for
tangency is obtained as follows;

i.e.
Examples
1. Prove that the parametric equation of the parabola are given by
X = at2, and y = 2at
Solution
Consider the line
Y = mx + c is a tangent to the parabola y2 = 4ax. Hence the condition for tangency is given
by y2 = 4ax

The parametric equation of the parabola of m is given as x = at2 and y = 2at
Where;
t – is a parameter
GRADIENT OF TANGENT OF THE PARABOLA
The gradient of tangent to the parabola can be expressed into;
i) Cartesian form
ii) Parametric form
i) IN CARTESIAN FORM
- Consider the tangent to the parabola y2 = 4ax Hence, from the theory.
Gradient of the curve at any = gradient of tangent to the curve at the
point

ii) IN PARAMETRIC FORM
Consider the parametric equations of the parabola
i.e.
EQUATION OF TANGENTS TO THE PARABOLA
These can be expressed into;
i) Cartesian form

ii) Parametric form
i) In Cartesian form
- Consider the tangent to the parabola y2 = 4ax at the point p (x, y)
Hence the equation of tangent is given by

ii) In parametric form
· Consider the tangent to the parabola y2 = 4ax at the point p (at2, 2at)
Hence the equation of tangent is given by;
Examples

1. Show that the equation of tangent to the parabola y2 = 4ax at the
point
2. Find the equation of tangent to the parabola y2 = 4ax at (at2, 2at)
NORMAL TO THE PARABOLA
Normal to the parabola is the line which is perpendicular at the point of tangency.
Where;
P is the point of tangency
GRADIENT OF THE NORMAL TO THE PARABOLA
This can be expressed into;·
i) Cartesian form
ii) Parametric form

- Consider the gradient of tangency in Cartesian form
i.e.
Let M = be gradient of the normal in Cartesian form but normal is perpendicular to tangent.
ii) In Parametric form
Consider the gradient of tangent in parametric form.
Let m be gradient of the normal in parametric form.
But
Normal is perpendicular to the tangent

EQUATION OF THE NORMAL TO THE PARABOLA
These can be expressed into;·
i) Cartesian form
ii) Parametric form
Consider the normal to the point y2= 4ax at the point p (x1, y1) hence the equation of the normal
given by;
ii) In parametric form
Consider the normal to the parabola y2 = 4ax at the point p (at2, 2at). Hence the equation
of the normal is given by;

Examples:
1. Find the equation of the normal to the parabola y2 = at the point
2. Show that the equation of the normal to the parabola y2 = 4ax at the point (at3, 2at) is
CHORD TO THE PARABOLA
· This is the line joining two points on the parabola

Let m – be gradient of the chord
Hence
ii) GRADIENT OF THE CHORD IN PARAMETRIC FORM
Consider a chord to the parabola at the points and

EQUATION OF THE CHORD TO THE PARABOLA.
These can be expressed into;·
i) Cartesian form
ii) Parametric form
i) EQUATION OF THE CHORD IN PARAMETRIC FORM
- Consider the chord to the parabola y2 = 4ax at the points .
Hence the equation of the chord is given by;

II. EQUATION OF THE CHORD IN CARTESIAN FORM.
Consider the chord to the parabola y2 = 4ax at the point P1(x1, y1) and P2 (x2, y2) hence the
equation of the chord is given by
EXCERSICE.

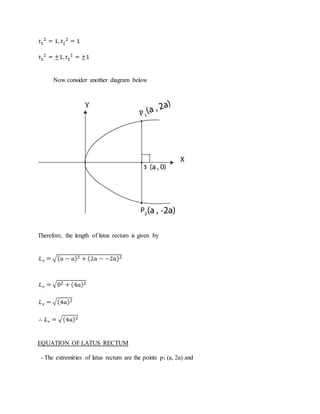
1. Show that equation of the chord to the parabola y2 = 4ax at (x1, y1) and (x2, y2) is
2. Find the equation of the chord joining the points ( ) and
3. As , the chord approaches the tangent at t1.deduce the equation of the tangent from the
equation of the chord to the parabola y2 = 4ax.
THE LENGTH OF LATUS RECTUM
Consider the parabola

Now consider another diagram below
Therefore, the length of latus rectum is given by
EQUATION OF LATUS RECTUM
- The extremities of latus rectum are the points p1 (a, 2a) and

p2 (a1, -2a) as shown below
Therefore, the equation of latus rectum is given by
OPTICAL PROPERTY OF THE PARABOLA
Any ray parallel to the axis of the parabola is reflected through the focus. This property which is
of considerable practical use in optics can be proved by showing that the normal line at the point
‘’p’’ on the parabola bisects the angle between and the line which is parallel to the axis
of the parabola.
Angle of INCIDENCE and angle of REFLECTION are equal

– is the normal line at the point ‘p’ on the parabola
i.e.

Note that; (QPS) Is an angle.
Examples
Prove that rays of height parallel to the axis of the parabolic mirror are reflected through the
focus.
TRANSLATED PARABOLA
1.
- consider the parabola below

PROPERTIES.
I) The parabola is symmetrical about the line y = d through the focus
II) Focus,
III) Vertex,
IV) Directrix,
2.
- Consider the parabola below

PROPERTIES
I) the parabola is symmetrical about the line x = c, through the focus
II) Focus
III) Vertex,
IV) Directrix,
Examples
1. Show that the equation represent the parabola and hence find
i) Focus
ii) Vertex

iii) Directrix
iv) Length of latus rectum
Solution
Given;

2. Shown that the equation x2 + 4x + 2 = y represents the parabola hence find its focus.
Solution
Given;

3. Show that the equation x2 + 4x – 8y – 4 = 0 represents the parabola whose focus is at (-2, 1)
Solution

ELLIPSE
This is the conic section whose eccentricity e is less than one
I.e. |e| < 1

AXES OF AN ELLIPSE
An ellipse has two axes these are
i) Major axis
ii) Minor axis
1. MAJOR AXIS
Is the one whose length is large
2. MINOR AXIS
Is the one whose length is small
a)

Where
AB – Major axis
PQ – Minor axis
EQUATION OF AN ELLIPSE
These are;
i) Standard equation
ii) General equation
1. STANDARD EQUATION
- Consider an ellipse below;

1st CASE
Consider an ellipse along x – axis

PROPERTIES
I) an ellipse lies along the x – axis (major axis)
ii) a > b

iii)
iv) Foci,
v) Directrix
vi) Vertices, (a, o), (-a, o) along major axis
(0, b) (0, -b) along minor axis
vi) The length of the major axis l major = 2a
viii) Length of minor axis l minor = 2b
Note:
For an ellipse (a – b) the length along x – axis
B – is the length along y – axis
2nd CASE
· Consider an ellipse along y – axis

PROPERTIES
i) An ellipse lies along y – axis (major axis)
ii) b > a
iii)
iv) Foci
v) Directrices
vi) Vertices: = along major

= along minor as
vii) Length of the major axis L major = 2b
viii) Length of the minor axis L minor = 2a
II. GENERAL EQUATION OF AN ELLIPSE
· Consider an ellipse below y – axis
From

EXAMPLE
Given the equation of an ellipse
Find i) eccentricity
ii) Focus
iii) Directrices
Solution
Given
Compare from

Find the focus and directrix of an ellipse 9x2 + 4y2 = 36
Solution
Given;

CENTRE OF AN ELLIPSE
This is the point of intersection between major and minor axes
· O – Is the centre of an ellipse
A – Is the centre of an ellipse
DIAMETER OF AN ELLIPSE.

This is any chord passing through the centre of an ellipse
Hence – diameter (major)
– Diameter (minor)
Note:
i) The equation of an ellipse is in the form of
ii) The equation of the parabola is in the form of
iii) The equation of the circle is in the form of
PARAMETRIC EQUATIONS OF AN ELLIPSE
The parametric equations of an ellipse are given as
And
Where
θ – Is an eccentric angle
Recall

TANGENT TO AN ELLIPSE
This is the straight line which touches the ellipse at only one point
Where;
P – Is the point of tangent or contact
Condition for tangency to an ellipse
Consider the line b = mx + c is the tangent to an ellipse

Examples
Show that, for a line to touch the ellipse Then,
GRADIENT OF TANGENT TO AN ELLIPSE
This can be expressed into;
i) Cartesian form
ii) Parametric form
1. GRADIENT OF TANGENT IN CARTESIAN FORM
- Consider an ellipse
Differentiate both sides with w.r.t x

ii. GRADIENT OF TANGENT IN PARAMETRIC FORM
- Consider the parametric equation of an ellipse

EQUATION OF TANGENT TO AN ELLIPSE
These can be expressed into;
i) Cartesian form
ii) Parametric form
I. Equation of tangent in Cartesian form
- Consider the tangent an ellipse
Hence, the equation of tangent is given by

EQUATION OF TANGENT IN PARAMETRIC FORM.

Consider the tangent to an ellipse At the point
Hence the equation of tangent is given by

EXERCISE
i. Show that the equation of tangent to an ellipse
ii. Show that the equation of tangent to an ellipse
iii. Show that the gradient of tangent to an ellipse
NORMAL TO AN ELLIPSE
Normal to an ellipse perpendicular to the tangent at the point of tangency.
Where: p is the point of tangency
GRADIENT OF THE NORMAL TO AN ELLIPSE.
This can be expressed into two
i) Cartesian form
ii) Parametric
I) IN CARTESIAN FORM

- Consider the gradient of the tangent in Cartesian form
But normal tangent
II) IN PARAMETRIC FORM
Consider the gradient of tangent in parametric form
Let m = slope of the normal in parametric form
EQUATION OF THE NORMAL TO AN ELLIPSE
This can be expressed into;
(i) Cartesian form
(ii) Parametric form
I. IN CARTESIAN FORM

- consider the normal to an ellipse
Hence the equation of the normal is given by

II) IN PARAMETRIC FORM
Consider the normal to an ellipse
Hence the equation of the normal is given by
Examples
· Show that the equation of the normal to an ellipse
CHORD OF AN ELLIPSE.

This is the line joining any two points on the curve ie (ellipse)
GRADIENT OF THE CHORD TO AN ELLIPSE.
This can be expressed into
i) Cartesian form
ii) Parametric form
I. IN CARTESIAN FORM
- Consider the point A (x1, y1) and B (x2, y2) on the ellipse hence the gradient of the
cord is given by
II. IN PARAMETRIC FORM
Consider the points A and B on the ellipse
Hence the gradient of the chord is given by;

EQUATION OF THE CHORD TO AN ELLIPSE
These can be expressed into
i) Cartesian form
ii) Parametric form
I: IN CARTESIAN FORM.
Consider the chord the ellipse at the point A (x1, y1) and B(x2,y2). Hence the
equation of the chord is given by;
II. IN PARAMETRIC FORM.
Consider the chord to an ellipse at the points . Hence the
equation of the chord is given by

FOCAL CHORD OF AN ELLIPSE.
This is the chord passing through the focus of an ellipse

Where = is the focal chord
Consider the points A and B are respectively Hence
Gradient of AS = gradient of BS
Where s = (ae, o)
DISTANCE BETWEEN TWO FOCI.
Consider the ellipse below;

2
2
2
Where a = is the semi major axis
e = is the eccentricity
DISTANCE BETWEEN DIRECTRICES.
Consider the ellipse below

=
=
Where a – is the semi major axis
e – is the eccentricity

LENGTH OF LATUS RECTUM.
Consider the ellipse below

IMPORTANT RELATION OF AN ELLIPSE
Consider an ellipse below

ECCENTRIC ANGLE OF ELLIPSE
.This is the angle introduced in the parametric equation of an ellipse
I.e
Where - is an eccentric angle
CIRCLES OF AN ELLIPSE
These are 1) Director Circle
2) Auxiliary circle
1. DIRECTOR CIRCLE
- This is the locus of the points of intersection of the perpendicular tangents.
Consider the line is tangent to the ellipse
Hence

2. AUXILIARY CIRCLE
- This is the circle whose radius is equal to semi – major axis

Using Pythagoras theorem
a – is the radius of the auxiliary circle
CONCENTRIC ELLIPSE.
These are ellipse whose centre are the same.
The equations of centric ellipse are;
Where a and b semi – major and semi – minor axes of the small ellipse

A and B are the semi – major and semi – minor axes of the large ellipse
A – a = B – b
A – B = a – b·
Is the condition for concentric ellipse
TRANSLATED ELLIPSE
This is given by the equation
A. PROPERTIES
i) An ellipse lies along x – axis
ii) a > b
iii) Centre (h, k)
iv) Vertices
v) Eccentricity,
vi) Foci
vii) Directrices
B. PROPERTIES
i) An ellipse has along y – axis
ii) b > a
iii) Centre (h, k)
iv) Vertices
v) Eccentricity
vi) Foci
Examples

Show that the equation 4x2 – 16x + 9y2 + 18y – 11 = 0 represents an ellipse and hence find i)
centre ii) vertices iii) eccentricity iv) foci v) directrices.
Solution

III. HYPERBOLA
This is the conic section whose eccentricity ‘’e’’ is greater than one ( e > 1)

The hyperbola has two foci and two directrices
Where S and S’ are the foci of the hyperbola hence
Where e > 1
EQUATION OF THE HYPERBOLA
There are;
i) Standard equation
ii) General equation
1. STANDARD EQUATION OF THE HYPERBOLA
Consider

COORDINATE GEOMETRY II

More Related Content

What's hot (20)

Similar to COORDINATE GEOMETRY II (20)

More from shahzadebaujiti (20)

Recently uploaded (20)

COORDINATE GEOMETRY II