Data structures and algorithm
- 1. 1 Data Structures and Algorithm Part 1 Anja Christin Kaiser Second Semester 2011 Ndejje University
- 2. 2 Content Figures ....................................................................................................................................................... 5 Tables ........................................................................................................................................................ 6 Introduction................................................................................................................................................... 7 Data Types..................................................................................................................................................... 9 General...................................................................................................................................................... 9 Standard Primitive Types........................................................................................................................... 9 Integer types.......................................................................................................................................... 9 Real type.............................................................................................................................................. 10 Boolean type........................................................................................................................................ 11 Char type ............................................................................................................................................. 11 Set type................................................................................................................................................ 13 Enumeration type................................................................................................................................ 14 Complex data types................................................................................................................................. 15 Array.................................................................................................................................................... 15 Matrix .................................................................................................................................................. 16 Vectors................................................................................................................................................. 16 Records/Structures.............................................................................................................................. 16 Representation of Data in the Computer................................................................................................ 18 Bit ........................................................................................................................................................ 18 Nibbles................................................................................................................................................. 18 Bytes.................................................................................................................................................... 19 Converting ........................................................................................................................................... 19 Bit operators........................................................................................................................................ 21 Searching Methods...................................................................................................................................... 24 Linear Search........................................................................................................................................... 24 Binary Search........................................................................................................................................... 25 Table Search ............................................................................................................................................ 27 Straight String Search.............................................................................................................................. 29 Algorithm..................................................................................................................................................... 31 Introduction............................................................................................................................................. 31
- 3. 3 Performance............................................................................................................................................ 32 Recursive ................................................................................................................................................. 33 Examples.............................................................................................................................................. 35 Recursion vs. Iteration......................................................................................................................... 36 Primitive Recursion Function .............................................................................................................. 38 Peano-Hilbert curve............................................................................................................................. 39 Turtle Graphics .................................................................................................................................... 40 The towers of Hanoi................................................................................................................................ 42 Permutation ............................................................................................................................................ 44 Backtracking and Branch-And-Bound...................................................................................................... 46 The n-queens problem ........................................................................................................................ 46 Chose the data structure..................................................................................................................... 50 Travelling Salesman............................................................................................................................. 50 NP-complete class ............................................................................................................................... 52 Sorting ......................................................................................................................................................... 54 Introduction............................................................................................................................................. 54 Sorting Algorithm .................................................................................................................................... 54 Indirect Sort......................................................................................................................................... 55 Distribution Sort .................................................................................................................................. 55 Stable Sorting ...................................................................................................................................... 55 Selection Sort....................................................................................................................................... 56 Insertion Sort....................................................................................................................................... 56 Quick Sort ............................................................................................................................................ 58 Bucket Sort or Bin Sort ........................................................................................................................ 60 Radix Sort............................................................................................................................................. 62 Merge Sort........................................................................................................................................... 63 Bubble Sort.......................................................................................................................................... 66 Comparing the algorithms....................................................................................................................... 67 Dynamic Data Structures............................................................................................................................. 68 Pointers ................................................................................................................................................... 68 Linear Lists............................................................................................................................................... 69
- 4. 4 Linked List............................................................................................................................................ 70 Circular List.......................................................................................................................................... 73 Doubly-Linked List ............................................................................................................................... 74 Stack .................................................................................................................................................... 77 Queues................................................................................................................................................. 79 Sorted List............................................................................................................................................ 80 Linked Lists vs. Dynamic Arrays........................................................................................................... 81 Tree structures ........................................................................................................................................ 81 General................................................................................................................................................ 81 Balanced Trees .................................................................................................................................... 82 Tree Representation............................................................................................................................ 83 Binary Trees......................................................................................................................................... 84 Sorted Binary Tree............................................................................................................................... 87 Binary Search Tree............................................................................................................................... 89 Insert a element in a Sorted Binary Tree............................................................................................. 89 Delete a node in a Sorted Binary Tree................................................................................................. 90 Looking for the next element in a Sorted Binary Tree: ....................................................................... 91 Other Tree Types................................................................................................................................. 91 References & Links ...................................................................................................................................... 94
- 5. 5 Figures Figure 1 Boolean Operators Truth Table..................................................................................................... 11 Figure 2 Table from http://www.ascii.cl/.................................................................................................... 12 Figure 3 Recursive Structure from http://dev.webcom-one.de/wp-content/uploads/2010/07/baum_j.png ..................................................................................................................................................................... 34 Figure 4 Recursive Structure from http://www.slideshine.de/ .................................................................. 34 Figure 5 Faculty Process.............................................................................................................................. 36 Figure 6 Peano-Hilbert Curve ...................................................................................................................... 39 Figure 7 Turtle Graphic C Program Output ................................................................................................. 42 Figure 8 Turtle Graphic................................................................................................................................ 42 Figure 9 Towers of Hanoi............................................................................................................................. 43 Figure 10 n-queen threats........................................................................................................................... 46 Figure 11 8-queen problem death end example......................................................................................... 47 Figure 12 n-queen problem with n = 4........................................................................................................ 48 Figure 13 Travelling Salesman..................................................................................................................... 51 Figure 14 NP-complete................................................................................................................................ 52 Figure 15 Insertion Sort............................................................................................................................... 57 Figure 16 Quick Sort .................................................................................................................................... 59 Figure 17 Bucket Sort Example.................................................................................................................... 61 Figure 18 Merge Sort................................................................................................................................... 64 Figure 19 Address Space.............................................................................................................................. 68 Figure 20 Pointer......................................................................................................................................... 69 Figure 21 Linked list..................................................................................................................................... 70 Figure 22 Insert a new node........................................................................................................................ 71 Figure 23 Insert Node at beginning............................................................................................................. 72 Figure 24 Remove a Node ........................................................................................................................... 72 Figure 25 Circular List.................................................................................................................................. 73 Figure 26 Circular List insert at beginning................................................................................................... 73 Figure 27 Doubly-Linked Lists...................................................................................................................... 74 Figure 28 Insert a Node in a Doubly Linked List .......................................................................................... 75 Figure 29 Remove a node in a Doubly Link List........................................................................................... 77 Figure 30 Comparing linked list/dynamic arrays from Wikipedia.org......................................................... 81 Figure 31 Level of a Tree ............................................................................................................................. 82 Figure 32 Balance Tree vs. Oriented Tree ................................................................................................... 83 Figure 33 Tree Representation.................................................................................................................... 83 Figure 34 Family Tree Noah and Prince Charles.......................................................................................... 84 Figure 35 Binary Tree .................................................................................................................................. 85 Figure 36 Binary Tree .................................................................................................................................. 85 Figure 37 Binary Tree Example.................................................................................................................... 86 Figure 38 Mathematical Formulas as Binary Tree....................................................................................... 87
- 6. 6 Figure 39 Inorder Traverse: 1 3 5 6 7 8 9..................................................................................................... 88 Figure 40 Balanced in heights but not balanced and a balanced Tree..................................... 89 Figure 41 Insert in a Sorted Binary Tree...................................................................................................... 90 Figure 42 Remove a node in a Sorted Binary Tree...................................................................................... 91 Tables Table 1Classification of Algorithm............................................................................................................... 32 Table 2 Standard Big-O Notations............................................................................................................... 33 Table 3 Variants of Bucket Sort................................................................................................................... 61 Table 4 Variants of Bubble Sort................................................................................................................... 66 Table 5 Comparing comparison sorts.......................................................................................................... 67 Table 6 Comparing other sorts.................................................................................................................... 67
- 7. 7 Introduction This course is designed to teach you a more efficient way how to implement program code. It is necessary that you • have some basic knowledge of programming in C (because we will use a lot of examples) • can write own simple programs in C What is a good program? These are same criteria for a good program code • runs correctly and efficiently • can be easy read and understand (not only by the programmer) • can be easy modified • can easily be debugged Definitions Correct means in accordance with its specifications Efficiently means in a minimum of time and with a minimum of memory used (performance). This can be reached by using the most appropriate data structure and algorithm. Opposite would be a way of implementation called hacking (producing a computer program rapidly, without thought and without any design methodology) or from the brain into the terminal (Vom Hirn ins Terminal). This course focuses on solving problems in an efficient way. Therefore it introduces a number of fundamental data structures and algorithm. Unfortunately a lot of problems arise from the failure of fulfilling the criteria mentation above (software crashes).The discipline of software engineering is concerned with building large software systems which perform as their users expected, are reliable and easy to maintain. However in this course we will concentrate on simple programs only to underline the principles of the algorithm or methods. By using these techniques in programming you will receive • efficient software programs • correct and fast programs • easier to modify and understand by other programmers
- 8. 8 Programming Strategies These are same basic programming strategies to build efficiently and reliably solutions: • Decomposing the program in small modules. Each of them can be written and tested independently • Splitting each task in a number of smaller tasks. Each of them is completed separately. The tasks can be split according to their function (the role it plays in the module) or structure (also called object orientation. It constructs software models of the behavior of real world items). Course outlines First we will have a look at the different data types (primitive and complex types) and their representation in computer systems. Also how converting is done will be showed in this chapter. The next chapter deals with searching methods and their strength and weaknesses. After this chapter we look at algorithm. After a general introduction we focus especially on recursive algorithm. We will have a closer look to same applications in computer science. Afterwards we will learn about two methods called backtracking and branch-and-bound. The fourth chapter deals with different sorting algorithms. Here we discuss the strength and weakness of each of them and try to compare them with each other. Sorting algorithms have a great use in computer programming and therefore they are very important. After this chapter we focus on dynamical data structure such as pointers and linear lists. We will see different types of linear lists especially in the context of sorting. Afterwards we get to know a structure called tree structure. We will have a closer look to some of them and if times allowed also discover together other tree structures. Tree structures are often used for sorting and searching. In the last chapter we will have a short look to hashing and the used in computer programming.
- 9. 9 Data Types General Definition A data type in programming is a classification of a particular type of information. It is easy for humans to distinguish between different types of data. Similarly, a computer uses special internal codes to keep track of the different types of data it processes. Most programming languages require the programmer to declare the data type of every data object, and most database systems require the user to specify the type of each data field. The available data types vary from one programming language to another, and from one database application to another. There are also some programming languages applying the data type of a variable out of the context the variable is used (for example Perl). Standard Primitive Types Standard primitive types are types available on most computers as build-in features. These types are: • Integer whole/integer numbers • Real real numbers • Boolean logical truth values • Char character • Set abstract data structure that can store certain values • Enumeration a set of named values Integer types Integer is a subset of the whole numbers. The size varies on different computer operating systems. If a computer uses n bits to represent an integer in two’s complement notation than all value x must satisfy: -2n-1 ≤ x < 2n-1 All operations on data of integer type are exact and correspond to the laws of arithmetic. The computation is truncated if the result lies outside the representable subset (overflow). The standard operators are: + Addition - Subtraction * Multiplication / Division with result real DIV Division with result integer MOD Modulo division r = q MOD p n*p + r = q where 0 ≤ r < n
- 10. 10 Examples 123 + 467 = 590 65 – 23 = 42 11 * 12 = 132 49 / 12 ~ 4.083 49 DIV 12 = 4 49 MOD 12 = 1 Real type Real data type is a subset of the real numbers. Real numbers are allowed to be inaccurate within the limits of round-off errors due to computation on a finite number of digits. This characteristic differ real data type from integer data type. The standard operators are: + Addition - Subtraction * Multiplication / Division with result real Because integer numbers are a subset of real numbers it is allowed to assign integer numbers to real numbers. The other way around is not commonly allowed (truncation required). Example Many programming languages do not include an exponentiation operator xn . The following is an algorithm for the fast computation of y = xn , where n > 0 is an integer and x and y are real numbers. float y = 1.0; int i = n; while (i > 0) { if (i % 2 != 0) y = y * x; x = x*x; i = i / 2; } Be x = 4 and n = 3: Round 1: i = 3 3 % 2 = 1 != 0 y = 1.0 * 4 = 4.0 x = 4 * 4 = 16
- 11. 11 i = 3 /2 = 1 Round 2: i = 1 1 % 2 = 1 != 0 y = 4.0 * 16 = 64 x = 16 * 16 = 256 1 = 1 / 2 = 0 y = 64 Boolean type The standard Boolean type has only two values TRUE and FALSE. The operators for the Boolean data type are: Logical conjunction & Logical disjunction OR Negations ~ Boolean Operators Be a and b two Boolean variables than the following truth table is valid: a b a & b a OR b ~a TRUE TRUE TRUE TRUE FALSE TRUE FALSE FALSE TRUE FALSE FALSE TRUE FALSE TRUE TRUE FALSE FALSE FALSE FALSE TRUE Figure 1 Boolean Operators Truth Table Note that comparisons are operations yielding in a result of type Boolean. In the most programming languages the operators & (also called AND) and OR have an additional property; a & b is still defined even if a or b are not defined. This conditionality is an important and useful property. Char type The data type char comprises a set of printable characters. There exists no general accepted standard character set on all computer systems. The most accepted set is the American Standard Code for Information Interchange (ASCII) defined by the International Standards Organization (ISO).
- 12. 12 Figure 2 Table from http://www.ascii.cl/ The table contains 95 printable characters and 33 control characters. There are several different character set tables depending on operating system and language. For example Windows is using a character set Windows 125x. To convert between different character sets so called Character Set Conversion Tables exist. As an agreement the minimal properties of the data type char are • The data type character contains: o 26 Latin letters in upper case o 26 Latin letters in lower case o 10 decimal digits o Additional letters like ä, ö, ü, â, etc. o Graphic characters like punctuation, quotation marks, etc.
- 13. 13 • The subset of letters and digits are ordered so that for example if A ≤ x ≤ Z implies that x is a capital letter • Every character has a hexadecimal and octal representation • The blank character and line-end character (non-printable) can be used as separators Definition Between the data type char and integer two standard type transfer functions exist. They are ORD(ch) returning the ordinal number of the character ch in the character set and CHR(i) returning the character with ordinal number i. They are invers to each other that means: ORD(CHR(i)) = i and CHR(ORD(c)) = c Example ORD(‘A’) = 65 CHR(100) = ‘d’ Definition Also another standard function CAP(ch) exists with the following definition: • be ch a lower-case letter than CAP(ch) = “the corresponding capital (upper-case) letter” • be ch a upper-case letter than CAP(ch) = ch Example CAP(‘b’) = ‘B’ CAP(‘C’) = ‘C’ Set type The data type set is an abstract data structure. It can store values without a particular order and no repetition. This data type implements the mathematical concept of a finite set. A set ranges from 0 to an integer value (for example 31).
- 14. 14 Examples a = {3} singleton set with one element 3 b = {x, y … z} set with elements, x, y, y+1… z-1, z c = {} the empty set The following operators are defined on variables of data type set: * Intersection/multiplication + Union/addition - Difference / Symmetric set difference IN membership The intersection operator has priority over union and difference operators. Examples r * s + t = (r * s) + t r – s * t = r – (s * t) r + s/t = r + (s/t) r IN s + t = r IN (s + t) Enumeration type A new primitive data type called enumeration type can be define by enumeration the distinct values belonging to it. TYPE type_name = (a1, a2, …, an), where type_name is the new type identifier and all ai are the new constant identifiers. Examples TYPE color = {yellow, red, green, blue) TYPE month = {January, February, March … December} TYPE day = {Monday, Tuesday … Sunday} TYPE currency = {Dollar, Euro, Pound, Shilling, Ruble, Yen}
- 15. 15 Complex data types Other data types are complex data type consists of standard data types. Array An array consists of elements of the same type (base type). An array has therefore a homogeneous structure and is a random-access structure that means all elements can be selected at random and they are equally accessible. To denote an element of an array is approached by the index. The index is an integer between 0 and n-1 when the array contains n element. n is called the size of the array. data_type array_name[n] TYPE array_name = ARRAY n OF data_type To access an element of the array using the index i: array_name[i] Example TYPE column = ARRAY 5 OF INTEGER int column[5]; TYPE NAME = ARRAY 32 OF CHAR char name[32]; Note Elements of an array are mostly selectively updated. The fact that the index is an integer has a most important consequence: indices can be computed. On the one side this generality provides a most powerful programming facility but on the other side is also gives rise to one of the most encountered programming mistakes: The calculate indices might be out of the range of the array. Example Implementation in C Finding the sum and max of an array implemented in C: int arr[n]; int sum = 0; for (i = 0; i < n; i++) sum = sum + arr[i]; int k = 0;
- 16. 16 int max = arr[0]; for (i = 1; i < n; i++) { if (max < arr[i]) { k = i; max = arr[k]; } } Matrix A matrix is an array whose elements are again arrays. Selectors may be concatenated accordingly, such that Mij or M[i][j] denote the jth component of row Mi, which is the ith component of M. This is usually abbreviated as M[i, j]. Example int matrix[4][3]; This is 4x3 matrix Vectors Vectors are much like arrays. Operations have the same effort as their counterparts on an array. Like arrays, vector data is allocated in contiguous memory. Unlike arrays vectors have no fixed size. They can grow. This can be done by adding more data or demand for it explicitly. In order to do this efficiently, the typical vector implementation grows by doubling its allocated space and has therefore often more space allocated than it needs because reallocating memory can sometimes be an expensive operation. Some programming languages offer a data type vector (Standard Template Library (STL) in C++, Java). It functions like a dynamic array. Records/Structures A structure or record data type is a join of elements of arbitrary types to a compound. In mathematics we have the example of the complex numbers composed of two real numbers or points in a coordinate system. Another example is a structure of data describing a person (first and last name, birthdate, sex, etc.)
- 17. 17 Definition A complex number is a number composed of a real and imaginary part. It can be written as: a + bi, where a and b are real numbers, i is the standard imaginary unit with i2 = −1. In mathematics such a compound type is the Cartesian product of its constituent types. The set of values defined by this compound type consists of all possible combinations of values, taken one from each set defined by each constituent type. The number of such combinations is also called n-tuples. It is the product of the number of elements in each constituent set. In data processing, composite types, such as descriptions of persons or objects, usually occur in files or data banks and record the relevant characteristics of a person or object. The word record (instead of Cartesian product) is widely accepted to describe a compound of data of this nature. A record or structure type R with components of types R1, R2 … Rn is defined as struct struct_name { r1: R1; r2: R2; … rn: Rn; } ; card (struct) = card(R1) * card(R2)*…*card(Rn) A component of a record is called field and the name is called field identifier. Example struct Date { int day; int month; int year; }; struct Person { char name[32];
- 18. 18 char firstname[32]; Date birthdate; }; struct Complex { float re; float im; }; Example Be p a Person than: p.name is from type Char p.birthdate is from type Date p.birthdate.day is from type Integer Node It is a characteristic of the Cartesian product that it contains all combinations of elements of the constituent types. But in practical applications not all of them are valid. For example the type Date includes the 35th May as well as the 31st November, dates which are not valid. It is in the responsibility of the programmer to make sure that invalid values not occur during execution of the program. Representation of Data in the Computer The data in Computer Systems are presented through a binary or two's complement numbering system. Bit A bit or binary digit is the smallest unit of data in computing. A bit representing only two different value interpreted by 0 and 1. But you can represent an infinite number of items with only one bit (true/false, red/blue, male/female, +/-, on/off) because the data are what you define them to be. Nibbles A collection of 4 bits is called nibble. Nibbles represent binary coded decimal (BCD) and hexadecimal number. You can display up to 16 distinct values. For hexadecimal number and BCD four bits are required for the representation.
- 19. 19 Hexadecimal: 0 1 2 3 4 5 6 7 8 A B C D E F BCD: 0 1 2 3 4 5 6 7 8 9 are represented by 4 bits. Bytes A byte is a collection of 8 bits and is the smallest addressable data item on the microprocessor. The bits of a byte are normally numbered from 0 to 7 by Bit 0: lower order bit or least significant bit Bits 0 – 3: low order nibble Bits 4 – 7: high order nibble Bit 7: high order bit or most significant bit A byte can represent 28 = 256 different values. It can represent number values from 0 … 255 or signed number from -128 to 127. The most important use for a byte is holding a character (see Char type). Converting The following processes are available to convert between binary, hexadecimal, octal and decimal data types. Converting Decimal to Binary • Dividing the decimal number with 2 (base of binary number system) • Note the remainder separately as the first digit from the right • Continually repeat the process of dividing until the quotient is zero • The remainders are noted separately after each step • Finally write down the remainders in reverse order Example 26/2 = 13 + 0 13/2 = 6 + 1 6/2 = 3 + 0 3/2 = 1 + 1 1/2 = 0 + 1 1 1 0 1 0
- 20. 20 Converting Decimal to Octal • Dividing the decimal number with 8 (base of binary number system) • Note the remainder separately as the first digit from the right • Continually repeat the process of dividing until the quotient is zero • The remainders are noted separately after each step • Finally write down the remainders in reverse order Example 26/8 = 3 + 2 3/8 = 0 + 3 32 Converting Decimal to Hexadecimal • Dividing the decimal number with 16 (base of hexadecimal number system) • Note the remainder separately as the first digit from the right. If it exceeds 9 convert it into the hexadecimal letter (10 to A, 11 to B, 12 to C, 13 to D, 14 to E, 15 to F). • Continually repeat the process of dividing until the quotient is zero • The remainders are noted separately after each step • Finally write down the remainders in reverse order Example 26/16 = 1 + 10 = 1 + A 1/16 = 0 + 1 1A Converting Binary, Octal and Hexadecimal to Decimal Each digit of the binary, octal or hexadecimal number is to be multiplied by its weighted position and each of the weighted values is added to get the decimal number. Example Binary 1 1 0 1 0 Weight 24 23 22 21 20 1*24 1*23 0*22 1*21 0*20 16 8 0 2 0
- 21. 21 Sum 16 + 8 + 0 + 2 + 0 = 26 Octal 3 2 Weight 81 80 3*81 2*80 24 2 Sum 24 + 2 = 26 Converting Between Octal and Hexadecimal • Converting each octal digit to a 3-bit binary form • Combine all the 3-bit binary numbers • Segregating the binary numbers into 4-bit binary form by starting the first number from the right bit (LSB) towards the number on the left bit (MSB) • Converting these 4-bit blocks into their respective hexadecimal symbols Example Octal 278 2 7 010 111 (3-bit binary form) 010111 0001 0111 (4-bit binary form) 1 7 Hex 1716 1 7 0001 0111 00 010 111 010 111 2 7 Note All conversions follow a certain pattern. If you convert from decimal you always use division. If you convert to decimal you always use multiplication. To convert between hexadecimal and octal you always convert into bits first. Bit operators Bit operators are a powerful and a very machine close concept. The following bit operators exist:
- 22. 22 & Bit-AND | Bit-OR ^ Bit-XOR ~ Bit-NOT (1 complement) << Bit left shift >> Bit right shift Bit-AND A combination of two integer numbers with Bit-And leads to: • If the bit is 1 in each number it is also 1 in the result. • If the bit is different or 0 in both numbers than also in the result the bit is 0 Example 1001 & 0101 0001 Bit-OR A combination of two integer numbers with Bit-OR leads to: • If the bit is 1 in one of the numbers the bit is also 1 in the result Example 1001 | 0101 1101 Bit-XOR (exclusive OR) A combination of two integer numbers with Bit-XOR leads to: • If the bit is 1 in only one of the numbers than the bit in the result is also 1 • Otherwise it is 0
- 23. 23 Example 1001 ^ 0101 1100 Bit-NOT Using this unary bit operator Bit-NOT leads to: • All bits are set which are not set before • All bits are set before are not set in the result Example ^1001 0110 Bit left shift Bit left shift leads to that all bits in the integer number are shifted to the left. All bits over the left border are deleted and on the right border 0s are added. Example 1001 << 2 0100 Bit right shift Bit right shift leads to that all bits in the integer number are shifted to the right. All bits over the right border are deleted and on the left border 0s are added. Example 1001 >> 2 0010
- 24. 24 Searching Methods Many different algorithms have been developed on searching methods. We assume that you search for a given element in a set of N elements represented as an array. The type item has a record structure with a field acting as a key. The task is to find an element x whose key field is equal to a given search element x. The result has index i so that: a[i].key = x Linear Search Linear search is to proceed sequentially through the array until the element you searched for is found. There are two conditions terminating the search: 1. The element is found that mean a[i].key = x 2. The element is not found in the array that means there was no element with a[i].key = x Example Algorithm int i = 0; while ((i < n) && (a[i] != x)) { i++; } It terminates when (i = N) or (a[i] = x). In this case the order of the condition is relevant. If i = N than no match exists. Because i is increased the repetition will reach an ending. You can alter the algorithm by using an additional element at the end of the array with value x. This element is called sentinel. Our array has therefore now N+1 elements with a[N] = x; Example Algorithm a[N] = x; i = 0; while (a[i] != x)) { i++; }
- 25. 25 It terminates when a[i] = x. If i = N that implies no match has found (beside the sentinel). Binary Search To speed up a search you need more information about the search data. If the data are ordered the search is much more effective. For example in a telephone book the data are alphabetically ordered. Assuming our data are order such that a[k-1] ≤ a[k] where 1 ≤ k ≤ N The algorithm based on: • if you pick an element a[i] at random and compare it with the search element than the search terminates if they are equal • if it is less than the search element than all elements with indices less or equal to i can be eliminated from the search • if it is greater than the search element than all elements with indices greater or equal to i can be eliminated This is called binary search. Be L the left and R the right end indices of the section in which elements still can be found. Algorithm L = 0; R = N – 1; found = false; while ((L ≤ R) && !found) { i = ”any value between L and R”; if (a[i] = x) found = true; else if (a[i] < x) L = i + 1; else R = i – 1; } The repetition ends when found is true or ((L > R) & (a[k] < x; 0 ≤ k < L) & (a[k] > x; R < k < N) which implies (a[i] = x) or (a[k] ≠ x; 0 ≤ k < N)
- 26. 26 The correctness of this algorithm does not depend on the chosen i but it does influence the effectiveness. You wish to eliminate as much elements as possible in each step. The optimal solution is to choose the middle element. This eliminates half of the array in any case. As a result the maximal number of step is log2N. For linear searches the number of comparisons to be expected is N/2. Example N = 1024 linear search: 612 binary search: 10 The algorithm can be also improved by chancing the second if clauses because if you test the equality as a second step it occurs only once and causes termination. Another improvement can be made if you chance the algorithm to: L = 0; R = N; while (L < R) { i = (L + R) / 2; if (a[i] < x) L = i + 1 else R = i; } The repetitions ends when L ≥ R. In each step L will be increased or R will be decreased and it ends when L = R. In contrast to the first solution this algorithm finds the matching element with the last index. Example Array a = {1, 4, 6, 9, 10, 15, 18, 23, 27, 34, 44} Searching for x = 27 L = 0 and R = 11 = N First Round: i = 11/2 = 5 a[i = 5] =15 < x = 27 L = 6 and R = 11 Second Round: i = 17/2 = 8 a[i = 8] = 27 = x L = 6 and R = 8 Third Round: i = (6+8)/2 = 7 a[i = 7] = 23 < x = 27 L = 8 and R = 8 Index = R = L = 8
- 27. 27 Table Search A search through an array is sometimes called a table search. This is particularly the case if the elements of the array are themselves structured object like numbers of characters. Definition An array of characters is also called a string. • Equality of strings is defined by: s = t ≡ (si = ti; 0 ≤ i ≤ N) • An order of strings is defined by: s < t ≡ (si = ti) & (sj < tj); 0 ≤ i ≤ j and 0 ≤ j < N To find a match between strings all characters have to be equal. This comparison can also be seen as a search of an unequal pair that means a search for inequality. If no unequal pairs exist the strings are equal. If the length of the strings is small a linear search can be used. The length of a string can be represented as: • A string is terminated by a specific terminating character. In the most cases the null character0 is used. • The length is stored at the first element of the array. Therefore the string s is represented as s = s0, s1, s2… sN-1 where s0 is the length = CHR(N) and s1, …, sN-1 are the characters of the string. In this solution the length is directly available. Algorithm i = 0; while ((s[i] == t[i]) && (s[i] != ‘0’)) { i++; } In this case the termination character 0 functions as a sentinel. The table search needs a nested search that means a search through the entries of the table and for each entry a sequence of comparisons between components. Be T a table of strings and s the search argument and N a large number and may the table be alphabetically ordered. Than we use a binary search.
- 28. 28 Algorithm L = 0; R = N; while (L < R) { i = (L + R) / 2; j = 0; while (T[i][j] = s[j]) & (s[j] != ‘0’) { j++; } if (T[i][j] < s[j]) L = i + 1; else R = i; } Example Table T = {Valarie, Valentine, Vance, Vanessa, Vaughn, Velma, Vera, Verity, Verna, Vernon, Veronica, Vicky, Victor, Victoria, Vincent, Viola, Violet, Vivian} Search string s = Victor L = 0, R = 18; First Round i = (0 + 18) / 2 = 9, j = 0 while T[9][0] = V = s[0] = V j = 1 T[9][1] = e != s[1] = i if L = 9 + 1 = 10 Second Round i = (10 + 18)/2 = 14, j = 0 while T[14][0] = V = s[0] = V j = 1 T[14][1] = i = s[1] = i j = 2 T[14][2] = n != s[2] = c if R = 14 Third Round i = (10 + 14)/2 = 12, j = 0 while T[12][0] = V = s[0] = V j = 1 T[12][1] = i = s[1] = i j = 2 T[12][2] = c = s[2] = c j = 3 T[12][3] = t = s[3] = t j = 4 T[12][4] = o = s[4] = o j = 5 T[12][5] = r = s[5] = r j = 6 if R = 12 Fourth Round i = (10 + 12)/2 = 11, j = 0 while T[11][0] = V = s[0] = V j = 1
- 29. 29 T[12][1] = i = s[1] = i j = 2 T[12][2] = c = s[2] = c j = 3 T[12][3] = k != s[3] = t j = 4 if L = 10 + 1 = 11 Fifth Round i = (11 + 12)/2 = 11, j = 0 while T[11][0] = V = s[0] = V j = 1 T[12][1] = i = s[1] = i j = 2 T[12][2] = c = s[2] = c j = 3 T[12][3] = k != s[3] = t j = 4 if L = 10 + 1 = 12 R = L = 12 Straight String Search A string search is to find an array in another array. Typically the elements of the arrays are characters. Than you can regard the one array as a text and the searching array as a pattern or word you wish to find in the text. In the most cases you look for the first appearance of the word in the text. The straight string search is a straightforward searching algorithm for this task. Definition Be s an array of N element and p an array of M element where 0 < M < N. Let i be the result index of the first occurrence of the searching array p in an array s than a predicate P is defined as: P(i, j): si+k = pk with 0 ≤ k < j. Because the first occurrence of the pattern is searched P(k, M) must be false for all k < i. Therefore you can define a condition Q(i) like Q(i) = ~P(k, M) with 0 ≤ k < i The search is formulated as an iteration of comparisons like i = -1; do { i++; found = P[i][M]; } while (!found && i != N - M);
- 30. 30 The best way is that the iteration for P is a search for inequality among the corresponding pattern and string characters. This leads to a Pseudo algorithm like: i = -1; do { i++; j = 0; while ((j < M)&& (s[i+j] == p[j]) { /*P[i][j+1]; //handling with the pattern j++; } } while (j != M && i != N - M); The term i = N – M implies the nonexistence of a match anywhere in the string. Other string searches • Knuth-Morris-Pratt String Search • The Boyer-Moore String Search
- 31. 31 Algorithm Introduction A set of introduction done sequentially is called an algorithm. Therefore an algorithm is a list of well- defined instructions to complete a given task. There is an initial state. The introductions are done as a series of steps. It is an effective method to solve a problem expressed as a finite sequence of steps but it is not limited to finite (nondeterministic algorithm). In many computer programs algorithms are defined to perform a specified task in a specific order like calculation the income of employees. It is important to define the algorithm rigorously that means that all possible circumstances for the given task should be handled. The criteria for each step must be clear and computable. The order of the steps performed is always critical to the algorithm. The flow of control is from the top to the bottom (top-down) that means from a start state to an end state. Termination might be given to the algorithm but some algorithm could also run forever without stopping. Description of algorithms is classified into 3 levels: • High-level description: Describing the algorithm by ignoring the implementation details • Implementation description: Describing the way the data are stored • Formal description: The most detailed lowest level description In computer systems an algorithm is defined as an instance of logic written in software in order to intend the computer machine to do something. Algorithms are classified by Class Description Recursion or iteration Algorithm makes references to itself repeatedly until a finale state is reached Logical Algorithm = logic + control. The logic component defines the axioms that are used in the computation, the control components determines the way in which deduction is applied to the axioms. Serial/parallel/distributed Algorithm performing task parallel Deterministic/Non-deterministic Deterministic algorithm solve the problem with exact decision at every step whereas non-deterministic solve problem by guessing through the use of heuristics.
- 32. 32 Exact/approximate Exact algorithms reach an exact solution; Approximation algorithms searching for an approximation close to the true solution Quantum algorithm Algorithm running on a realistic model of quantum computation Table 1Classification of Algorithm Example Implementation in C gcd(x,y) = Greatest common divisor of the integer x and y: int mygcd(int x, int y) { int gcd = 0; if (y == 0) gcd = x; else gcd = mygcd(y, x % y); return gcd; } Examples gcd(34, 16) = gcd (16, 2) = gcd (2, 0) = 2 gcd(127, 36) = gcd(36, 19) = gcd (19, 17) = gcd(17, 2) = gcd (2, 1) = gcd (1, 0) = 1 Performance Performance in computer system plays a significant rule. The performance is general presented in the O- Notation (invented 1894 by Paul Bachmann) called Big-O-Notation. Big-O-Notation describes the limiting behavior of a function when the argument tends towards a particular value or infinity. Big-O- Notation is nowadays mostly used to express the worst case or average case running time or memory usage of an algorithm in a way that is independent of computer architecture. Definition Be n the size of the data or any other problem related size. f(n) = O(g(n)) for n ϵ N, if M, n0 ϵ N exist such that |f(n)| ≤ M|g(n)| for all n ≥ n0 Simpler: f(n) = O(g(n)) for n ∞
- 33. 33 The formal definition of Big-O notation is not used directly. The O-notation for a function f(x) is derived by the following rules: • If f(x) is a sum of several terms the one with the largest growth rate is kept and all others are ignored • If f(x) is a product of several factors, any constants (independent of x) are ignored Example f(x) = 7x3 – 3x2 + 11 The function is the sum of three terms: 7x3 , -3x2 , 11. The one with the largest growth rate it the one with the largest exponent: 7x3 . This term is a product of 7 and x3 . Because 7 don’t depend on x this factor can be ignored. As a result you got: f(x) = O(x3 ) List of standard Big-O Notations for comparing algorithm Big-O Description O(1) Constant effort, independent from n O(n) Linear effort O(n logn) Effort of good sort methods O(n2 ) Quadratic effort O(nk ) Polynomial effort (with fixed k) O(2U ) Exponential effort O(n!) All permutation of n elements Table 2 Standard Big-O Notations Other performance notations • theta, • sigma, • small-o Recursive Many problems, models and phenomenon have a self-reflecting form in which the own structure is contained in different variants. This can be a mathematical formula as well as a natural phenomenon.
- 34. 34 Example Figure 3 Recursive Structure from http://dev.webcom-one.de/wp-content/uploads/2010/07/baum_j.png Figure 4 Recursive Structure from http://www.slideshine.de/ If this structure is adopted in a mathematical definition, an algorithm or a data structure than this is called a recursion. Definition Recursion is the process of repeating items in a self-similar way. Recursion definitions are only reasonable if something is only defined by himself in a simpler form. The limit will be a trivial case. This case needs no recursion any more.
- 35. 35 Examples Language Even in languages you will find recursion: "Dorothy, who met the wicked Witch of the West in Munchkin Land where her wicked Witch sister was killed, liquidated her with a pail of water." Out of the sentences: “Dorothy met the Wicked Witch of the West in Munchkin Land” “Her sister was killed in Munchkin Land” “Dorothy liquidated her with a pail of water” A common joke is the following "definition" of recursion. (Catb.org. Retrieved 2010-04-07.) Recursion See "Recursion". Mathematic Examples for mathematical recursion are: Faculty F(n) = n! for n> 0 is defined F(0) = 1 F(n) = n * F(n-1) for n>0 Program code in C/C++ int faculty(int number) { if (number <= 1) return number; return number * (faculty(number - 1)); } Process: Calculate F(5) = 5! = 120
- 36. 36 Figure 5 Faculty Process Note Because of recursion it is possible that more than one incarnation of the procedure exists at one time. It is important that there is finiteness in the recursion. For example a query decided if there is another recursion call or not. Fibonacci sequence (classical example of recursion) F(0) = 0 (base case) F(1) = 1 (base case) F(n) = F(n-1) + F(n-2) (recursion) for all n > 1 with n ϵ N Recursion vs. Iteration Use of recursion in an algorithm has both advantages and disadvantages. The main advantage is usually simplicity. The main disadvantage is often that the algorithm may require large amounts of memory if the depth of the recursion is very large. Many problems are solved more elegant and efficient if they are implemented by using iteration.
- 37. 37 This is especially the case for tail recursion which can be replaced immediately by a loop, because no nested case exists which has to be represented by a recursion. The recursive call happens only at the end of the algorithm. Recursion and iteration are not really contrasts because every recursion can also be implemented as iteration. There are two ways to implement a recursion: • Starting from an initial state and deriving new states which every use of the recursion rules. • Starting from a complex state and simplifying successive through using the recursion rules until a trivial state is reached which needs no use of recursion. How to build a recursion depends mainly on: • How readable and understandable the alternative variants are • Performance and memory issues Tail recursion int tail_recursion(…) { if (simple_case) /*do something */; else /*do something */; tail_recursion(…); } Example The faculty algorithm is more efficient if you use an iterative implementation int faculty(int number) { int result = 1; while (number > 0) { result *= number; number--; ] return number; }
- 38. 38 Example Ackermann function as recursion int ackermann(int x, int y) { if (x == 0) return y + 1; else if (x == 0) return ackermann(x – 1, 1); else return ackermann(x – 1, ackermann(x, y – 1)); } The ackermann function is an example where it is more efficient and simpler to implement it with recursion. Primitive Recursion Function Definition The primitive recursive functions are among the number-theoretic functions, which are functions from the natural numbers (non negative integers) {0, 1, 2 , ...} to the natural numbers. These functions take n arguments for some natural number n and are called n-ary. The basic primitive recursive functions are given by these axioms: - Constant function: The 0-ary constant function 0 is primitive recursive. - Successor function: The 1-ary successor function S, which returns the successor of its argument, is primitive recursive. That is, S(k) = k + 1. - Projection function: For every n ≥ 1 and each i with 1 ≤ i ≤ n, the n-ary projection function Pi n , which returns its ith argument, is primitive recursive. More complex primitive recursive functions can be obtained by applying the operations given by these axioms:
- 39. 39 Peano-Hilbert curve Figure 6 Peano-Hilbert Curve The Peano-Hilbert curves were discovered by Peano and Hilbert in 1890/1891. They convert against a function. This function map the interval [0,1] of the real numbers surjective on the area [0,1] x [0,1] and is in the same time constant. The Peano-Hilbert Curve can be expressed by a rewrite system (L-system). Alphabet: L, R Constants: F, +, − Axiom: L Production rules: L → +RF−LFL−FR+ R → −LF+RFR+FL− F: draw forward +: turn left 90° -: turn right 90° Implementation in C #include <stdio.h> #include <stdlib.h> void f(int x, int y, int m) { x = m - abs(m-x); if (x == m || y == m ) { putchar(x == 0 || y == m+1 ? '@' : ' '); } else { if (y>m) f(x, y&m, m/2); else
- 40. 40 f(y, x, m/2); } } int main(void) { int z; for (z = N*N; z > 0; z--) { f(z % N, z/N, N/2); putchar(z%N ? ' ' : 'n'); } return 0; } Output @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ Turtle Graphics Turtle Graphics are connected to the program language Logo (1967). There is no absolute position in a coordination system. All introductions are relative to the actual position. A simple form would be: Alphabet: X, Y Constants: F, +, − Production rules: Initial Value: FX X → X+YF+ Y -FX-Y F: draw forward +: turn left 90° -: turn right 90°
- 41. 41 Implementation in C #include <stdio.h> #include <stdlib.h> void X(int n); void Y(int n); void X(int n) { if (n > 0) { X(n-1); printf("_"); Y(n-1); printf("|"); printf("_"); } } void Y(int n) { if (n > 0) { printf("-"); printf("|"); X(n-1); printf("-"); Y(n-1); } } int main(void) { printf("Initn"); printf("|"); X(10); printf("nFinish"); return 0; } Output
- 42. 42 Figure 7 Turtle Graphic C Program Output Other turtle graphic Figure 8 Turtle Graphic The towers of Hanoi The towers of Hanoi is a mathematical game or puzzle. The Game • There are three rods with n disks in different sizes. At first they are all placed at the first rod. • The disks have to be placed in order so that a bigger size disks is not on top of a smaller size disk. • The objective of the puzzle is to move the entire stack to another rod, obeying the following rules: o Only one disk may be moved at a time o Each move consists of taking the upper disk from one of the rods and sliding it onto another rod, on top of the other disks that may already be present on that rod o No disk may be placed on top of a smaller disk. This game was developed at 1883 by a French mathematician Édouard Lucas
- 43. 43 Figure 9 Towers of Hanoi To solve this game that means moving n disks from rod a to b the following process is considered: • the first n-1 disks are moved from rod a to rod c • than the last disk remaining on a are moved to b • than n-1 disks are moved from c to b That means the roles of the three rods are always different In total you need 2n – 1 moves. This is minimal. Pseudo code void MoveDisks(int n, int from, int to, int help) { if (n > 0) { MoveDisks(n – 1, from, help, to); MoveDisk(from, to); MoveDisks(n – 1, help, to, from); } }
- 44. 44 MoveDisks(3, 1, 3, 2) MoveDisks(2, 1, 2, 3) MoveDisks(3, 1, 3, 2) MoveDisks(2, 1, 2, 3) MoveDisks(2, 1, 2, 3) MoveDisks(1, 1, 3, 2) MoveDisk(1, 3) MoveDisk(1, 2) MoveDisks(2, 2, 3, 1) MoveDisks(1, 3, 2, 1) Permutation A permutation is a sequence of n different object in a row. There are n! different permutations for n objects. Example A permutation of the three objects a, b, c would be: abc, acb, bac, bca, cab, cba n = 3 3! = 6 permutations Example implementation in C #include <stdio.h> #define SIZE 5 void swap(char &ch1, char &ch2) { char tmp = 0; tmp = ch1; ch1 = ch2; ch2 = tmp; }
- 45. 45 void permutation(char list[], int start, int max) { int i; if(start == max) { for(i = 0; i < SIZE; i++) printf("%c", list[i]); printf("n"); } else { for(i = start; i < max; i++) { swap(list[i], list[max - 1]); permutation(list, start, max - 1); swap(list[max - 1], list[i]); } } } int main() { char my_list[5] = {'a','b','c','d','e'}; permutation(my_list, 0, SIZE); return(0); } Problem Generate all possible permutation out of n object. Solution Two solution methods exist for this problem: Method1 For each permutation a1 a2 … an-1 you generate n new ones by putting the number n at all possible places: n a1 a2 … an-1 a1 n a2 …. an-1 …. a1 a2 … an-1 n Method2 For each permutation a1 a2 … an-1 an integer k with 1 ≤ k ≤ n is added an each ai is increased by 1 if ai ≥ k.
- 46. 46 Example From the permutation 231 we got by adding 1, 2, 3, and 4 to the permutation: 3421 3412 2413 2314 The second method is more efficient if the permutation are placed in an array because disarrange of parts of the array is not necessary. Backtracking and Branch-And-Bound The n-queens problem This is a part of the chess game. Challenge: Find a position for n queens on a n x n chessboard such that they not threaten each other. Idea • Build up a solution step by step by putting each queen one by one on the chessboard • If there is no possible place left for the queen k the (k-1) queen is removed from the chessboard and placed on a not already tried position • This is done as long as a solution is found or all possibilities are tried A queen on a chessboard threaten all fields • in the same row • in the same column • on both diagonals Definition A method in which every possibility is tested and in the case of a death end the step before is withdrawn and a new variant is tested is called a backtracking method. Figure 10 n-queen threats
- 47. 47 A death end in the n-queen problem for n = 8 would be the following illustration: Figure 11 8-queen problem death end example It is not possible to set another queen. To find a solution you have to remove all queens beside the first one. Only if the second queen is placed from C7 to E7 (or F7/G7) a solution can be found. In the most solution methods for backtracking it is very important to see as early as possible death ends to avoid a performance increase. Backtracking is a systematical search in the whole set to find acceptable states. In the case of the n-queen problem you have (n2 !)/(n2 – n)! possibilities to place n queens on a chessboard. For n = 8 this are 64!/56! ~ 1014 possibilities. An extreme performance killing case if you try every possibility. If you try a step by step method for backtracking you have to consider that • The numbers of possible moves are limited in a clever way • To check immediately if the solution part still fulfill the necessary criteria which are needed for the whole solution If you look at the n-queen problem it is therefore necessary to: • consider for the queen k only the k-te row on the chessboard for the next position • To check for each new queen immediately if she is threaten by the other queens on the chessboard. Example n = 4
- 48. 48 Figure 12 n-queen problem with n = 4 There are 16!/12! = 43 680 possibilities to set 4 queens on a 4x4 chessboard. If you consider only the k row for the queen k than the number of possibilities is reduced to nn . In this case: 44 = 256. If you threw away all position where even less then n queens threaten each other than you have only 17 possibilities left. Under these possibilities there are only 2 solutions and 4 death ends. Example implementation in C # include <stdio.h> # include <stdlib.h> # include <time.h> int flag; int number_of_queens = 0; void printArray(int arr[]);
- 49. 49 void getPositions(int arr[], int n1, int n2); int main() { int *arr_queen; int iterator = 0; printf("-----------------------n-Queens Problem------------------- --n"); printf("Please enter the number of rows(n) for the nxn chessboard: n"); scanf("%d", &number_of_queens); arr_queen = (int *)(malloc(sizeof(int)*number_of_queens)); printf("The rows and columns are numbered from 1 to n and the given solution has form (row, col).n"); printf("All possible solutions are: n"); for(iterator = 0; iterator < number_of_queens; iterator++) getPositions(arr_queen, 0, iterator); getchar(); } void printArray(int arr[]) { int i = 0; static int counter = 0; counter++; printf("Solution: # %d: ", counter); for(i = 0; i < number_of_queens; i++) printf("(%d, %d) ", i + 1, arr[i] + 1); printf("n"); } void getPositions(int arr[], int colno, int val) { int iterator1 = 0, iterator2 = 0; arr[colno] = val; if(colno == number_of_queens - 1) { printArray(arr); return; } for(iterator1 = 0; iterator1 < number_of_queens;) { for(iterator2 = 0; iterator2 <= colno; iterator2++) if(arr[iterator2] == iterator1 ||
- 50. 50 (colno + 1 - iterator2)*(colno + 1 - iterator2) == (iterator1 - arr[iterator2])*(iterator1 - arr[iterator2])) goto miss1; getPositions(arr, colno + 1, iterator1); miss1: iterator1++; } } Output Please enter the number of rows (n) for the nxn chessboard: 4 The rows and columns are numbered from 1 to n and the given solution has form (row, col). All possible solutions are: Solution: # 1: (1, 2) (2, 4) (3, 1) (4, 3) Solution: # 2: (1, 3) (2, 1) (3, 4) (4, 2) Chose the data structure The efficiency of the backtracking algorithm depends strongly on the chosen data structure. How efficient is • The check if a solution is reached • The identification of possible steps in a given situation • The check of the usefulness of a part solution • The execution of a step If possible each step should have an effort of O(1). You can improve for example the implementation of the n-queen problem if you save the amount of threaten row, columns and diagonals. Travelling Salesman Another problem is the travelling salesman. Description • Be n a number of place in a n x n distance matrix M where Mi,j is the distance between the places i and j. • Seek for the route with the minimal length such that all places are reached exactly one time and then return to the starting point.
- 51. 51 If you seek for an optimization or improvement than a lot of branches can be cut off which are only produce inefficient solutions. Figure 13 Travelling Salesman Definition A Branch-and-bound method is a general algorithm for finding an optimal solution of various optimization problems. It consists of a systematic enumeration of all possible solutions where inefficient solutions are eliminated by using upper and lower estimated bounds. Be L the solution space and c: L R a function and lo a solution to find such that: c(lo) ≤ k for a given bound k or c(lo) ≤ c(l) for all l ϵ L (global minimum) In backtracking it is reasonable to find another function c’: L R such that c’ is an estimate efficient lower bound for all part solution l’ ϵ L’ for all c(l) with l ϵ L. l’ is derived from l. The function c’ can be used to decide if it is efficient to pursue this part solution l’ or if it would be better to cut this brunch. In the travelling salesman problem L is the amount of all permutation over all the places 1…n and the function c the length of a route. The function for a part solution can consider the already travelled distance and an approximation for the length of the route to the not reached places. If you just try every permutation the effort is O(n!) (or O((n-1)!). The branch-and-bound method helps to reduce the effort but this is not a grantee.
- 52. 52 There is still no algorithm to really reduce the effort. The problem is therefore computationally difficult but a large number of heuristics and exact methods are known, so that some instances with tens of thousands of cities can be solved. This problem belongs to a set of so called NP-complete problems. The theory is that if you solve one of the NP-complete problems all of them are solvable Other branch-and-bound problems • Canadian traveller problem • Vehicle routing problem • Route inspection problem • Set TSP problem • Seven Bridges of Königsberg • Traveling repairman problem (minimum latency problem) • Traveling tourist problem • Tube Challenge NP-complete class In computational complexity theory, the complexity class NP-complete (NP-C or NPC) is a class of decision problems. A problem L is NP-complete if it has two properties: • It is in the set of Nondeterministic Polynomial Time (NP) problems: Any given solution to L can be verified quickly (in polynomial time) • It is also in the set of NP-hard problems: Any NP-problem can be converted into L by a transformation of the inputs in polynomial time Euler diagram for P, NP, NP-complete, and NP-hard set of problems It is still unknown if P = NP or P ≠NP Figure 14 NP-complete
- 53. 53 A given solution to such a problem can be verified quickly. There is no known way so far to locate a solution in the first place that means no fast solution is known to the NP-complete problems. This implies that the time required solving the problem using any known algorithm increase very quickly. Even for moderately large version of many of these problems the required time reaches into billions of years. Therefore one of the unsolved problems in computer science today is the so called P versus NP problem.
- 54. 54 Sorting Introduction Sorting is the rearranging of a given set of objects in a specific order. The purpose is often to simplify a search on the set later. Sorting is done for example in telephone books, data warehouses, libraries, databases, etc. The structure of the data dramatically influences the sorting algorithm. Each sorting algorithm has its advantages and disadvantages. These have to be weighed against each other in order to choose the proper sorting algorithm for the given set of objects. There exists a great diversity of sorting algorithm. To choose a proper algorithm it is necessary to understand the significant of performance. Sorting algorithm are classified in two categories which are sorting of arrays and sorting of files. They are also called internal and external sorting because arrays are stored in the internal store of a computer and files are stored on external devices (disks, folder). Definition If we have a number n of items a0, a1, …, an-1 a sorting algorithm gains in permuting these items into an array ak0, ak1, …, ak(n-1) so that for a given order function f: f(ako) ≤ f(ak1) ≤ … ≤ f(ak(n-1)) The value of the ordering function is called the key of the item. A sorting method is called stable (see Stable Sorting) if the relative order of items with equal keys remains unchanged by the sorting process. Now a closer look to some sorting algorithm is done. This is not a complete list of all existing sorting algorithm. Sorting Algorithm The steps in every sorting algorithm can be simplify by Selecting and inserting Interchanging Spreading and collection Distributing
- 55. 55 A sorting problem must not be numerical it must be only be distinguishable (e.g. by colors, by size). Therefore it must be possible for a sorting algorithm to decide if an element of the set is smaller than another element. For example you can make a numbered list for colors. In numerical values the compiler automatically knows how to treat them. For characters you can use for example the ASCII table to decide how the sorting is done. All the algorithms now discussed work with numerical representations where a smaller-, bigger-, same- relation is defined. Indirect Sort If you keep a list with references to a record the necessary time for swapping the data in the record can be drastically reduced. Afterwards the record is still untouched. But the array with references helps to rearrange the data in the record. The necessary time increases in linear fashion with the number of data in the record. This is called Indirect Sort. Definition Be A an array, n the number of elements in the array. Than an auxiliary array P is defined by P[i] = i for all i = 1, 2 …, n and the objective is to modify P so that A[P[1]] ≤ A[P[2]] ≤ … ≤ A[P[n]] Therefore instead of change the array A we change the array P. An Indirect Sort is indicated when the costs for swapping the data is high and the additional memory cause no problem. Distribution Sort A sorting algorithm is called a Distribution Sort if the data is distributed from its input to a multiple temporary structure. This structure is collected and placed on the output. Stable Sorting For some data you wish to sort them by more than one criterion. For example in a list of address you sort first by the last name and the last names by the first names. A sorting algorithm is called stable when
- 56. 56 one sort does not destroy the result of the previous sort. That means if the elements of the input array with the same value appear in the output array in the same order as they did in the input array. A not stable algorithm therefore needs more effort in getting the same result. First you sort the list by last name and then each block of identical last name you sort by the first names. Example List of pairs to order: {(3, A), (1, C), (2, B), (3, D), (1, B), (2, A), (3, C)} Two possibilities to sort them: {(1, B), (1, C), (2, A), (2, B), (3, A), (3, C), (3, D)} (order changed) {(1, C), (1, B), (2, B), (2, A), (3, A), (3, D), (3, C)} (order maintained) Selection Sort A Selection Sort compares the keys of the data to decide if they have to be swapped or not. It starts with the first element and checks all other elements if their key value is smaller. If so, the elements are swapped. If no smaller key can be found the algorithm continues with the next element. That means that almost every key is compared with the other keys. The needed time for this algorithm can be estimate by T = B * n2 where B is a constant reflecting the implementation and n the number of elements. If there are only two elements in the record this algorithm is faster than all others. Example if (x < y) { tmp = x; x = y; y = tmp; } Insertion Sort Every repetition of the Insertion Sort removes an element of the original input data. This element is put in the correct position of the already sorted part of the original data. The repetition takes place until no element is remaining. The choice of the element is arbitrary. Be s the element to be sorted:
- 57. 57 sorted part unsorted data ≤ s >s s … ≤ s s >s … Figure 15 Insertion Sort Algorithm #include "stdio.h" void sort(int arr[]) { int i = 0, j = 0, k = 0, temp = 0; for (i = 1; i < 5; i++) { for (j = 0; j < i; j++) { if (arr[j] > arr[i]) { temp = arr[j]; arr[j] = arr[i]; for (k = i; k > j; k--) arr[k] = arr[k - 1]; arr[k + 1] = temp; } } } } void main( ) { int arr[5] = {25, 17, 31, 13, 2}; int i = 0; printf ("Insertion sortn"); printf ("Array before sorting:n"); for (i = 0; i < 5; i++) printf ("%dt", arr[i]); sort(arr); printf("nArray after sorting:n"); for (i = 0; i <= 4; i++) printf ("%dt", arr[i]); }
- 58. 58 Ouput Insertion sort Array before sorting: 25 17 31 13 2 Array after sorting: 2 13 17 25 31 Example 5 7 0 3 4 2 6 1 (3) 3 5 7 0 4 2 6 1 3 4 5 7 0 2 6 1 0 3 4 5 7 2 6 1 0 1 3 4 5 7 2 6 0 1 2 3 4 5 7 6 0 1 2 3 4 5 7 6 0 1 2 3 4 5 6 7 Complexity Best case performance O(n) Average case performance О(n2 ) Worst case performance О(n2 ) Quick Sort In the Quick Sort algorithm we use a so called pivot element. The pivot element is selected in such a way that around half of the keys are smaller and half of the keys are bigger in the total record data. The data are separated accordingly into a sub part and high part. Equal elements can be put in one of both parts. We repeat the method recursively with each part. If a part has no element or one element it is defined as sorted. This is called partition operation. The needed time for this algorithm is estimated by T = C*n*log(n) where C is a constant reflecting the implementation and n the number of elements. Quick Sort is used where time is not a constraint. It is in general not a stable sort.
- 59. 59 <pivot pivot >pivot <pivot’ pivot’ >pivot’ pivot <pivot’’ pivot’’ >pivot’’ Figure 16 Quick Sort Example Algorithm void swap(int *a, int *b) { int t = *a; *a = *b; *b = t; } void sort(int arr[], int beg, int end) { if (end > beg + 1) { int piv = arr[beg]; int l = beg + 1; int r = end; while (l < r) { if (arr[l] <= piv) l++; else swap(&arr[l], &arr[--r]); } swap(&arr[--l], &arr[beg]); sort(arr, beg, l); sort(arr, r, end); } } Simple Algorithm quicksort( void *a, int low, int high ) { int pivot; if ( high > low ) { pivot = partition(a, low, high); quicksort(a, low, pivot-1); quicksort(a, pivot+1, high); }
- 60. 60 } Example (3 2 6 1 8 4 9 7 5) (3 2 6 1 4 7 5) (8 9) (1) (3 2 6 4 7 5) (8) (9) (1) (3 2) (4) (6 7 5) (8) (9) (1) (2) (3) (4) (6 5) (7) (8) (9) 1 2 3 4 5 6 7 8 9 The pivot element is chosen randomly for example the middle index of the list or the median of the first, middle and last element. A simple Quick Sort algorithm performs very badly on already sorted array of data. Performance of Quick Sort Best case performance O(n log n) Average case performance O(n log n) Worst case performance O(n2) Bucket Sort or Bin Sort Bucket Sort partitioning an array into a number of buckets. Each of these buckets is sorted individually. This can be done by using another sorting algorithm or again the bucket sort. A bucket sort is a distribution sort. These are the steps to be performed: • Set up an array of empty buckets • Put every item of the original array in its bucket • Sort each of the buckets which are not empty • Put all the elements now sorted back to the original array Algorithm buckets = empty array of n buckets for (int i = 0; i < length(array); i++)
- 61. 61 put (array[i], buckets[msbits(array[i], k)]; for (int j = 0; j < n; j++) next-sort(buckets[j] return concat(buckets[0] , buckets[1], …, buckets[n-1]) msbits(x, k) returns the k most significant bits of x. Of course different functions can be used to arrange the element in the buckets. Example 33, 41, 22, 8, 4, 12, 19, 37, 45, 7, 17, 26, 29, 34 Bucket 0-9 Bucket 10-19 Bucket 20-29 Bucket 30-39 Bucket 40-49 Variants of Buckets Sort are Name Description Generic bucket sort operates on a list of n numeric inputs between 0 and a maximum value Max and divided the value range into n buckets with size Max/n. Proxmap sort operates by dividing an array of keys into buckets and sorting the data than by using a mapkey function to characterize the data Histogram sort operates by adding an initial pass that counts the number of elements that will be put in each bucket using a count array. This information can be used to arrange the array values into a sequence of buckets in-place by a sequence of exchanges avoiding space overhead for bucket storage Postman’s sort operates on hierarchical structure elements. It is used by letter-sorting machines. Mail is sorted first between nation and international, then state, province, district, city, streets/routes, etc. The keys are not sorted against each other. Time is O(cn) where c depend on the size of the key and number of buckets. Shuffle sort operates by removing the first 1/8 of the elements n, sorts them recursively and puts them in an array. It creates n/8 buckets to which the remaining 7/8 elements are distributed. Each bucket is sorted and concatenated into a sorted array Table 3 Variants of Bucket Sort 8 4 7 12 19 17 22 26 29 33 37 34 41 45 Figure 17 Bucket Sort Example
- 62. 62 Radix Sort A very old sorting algorithm (invented 1887 by Herman Hollerith) is the Radix Sort. The Radix sort was used to sort cards. In general it sorts integers but it is not limited to it (e.g. characters can be represented by numbers). The algorithm distributes items to a bucket according to the item’s key part beginning with the least significant part of the key. After each round the items are recollected from the buckets. The process is repeated with the next most significant part of the key and so on. This is called Least Significant Digit Radix Sort (LSD). Example Input keys: 34, 12, 42, 32, 44, 41, 34, 11, 32, 23 4 buckets, because 4 different digit 1, 2, 3, 4 Sorting by the least significant digit: 1. Bucket: 41 11 2. Bucket: 12 42 32 32 3. Bucket: 23 4. Bucket: 34, 44, 34 Recollecting: 41 11 12 42 32 32 23 34 44 34 Sorting by the next most significant digit (here the highest digit): 1. Bucket: 11 12 2. Bucket: 23 3. Bucket: 32 32 34 34 4. Bucket: 41 42 44 Recollecting: 11 12 23 32 32 34 34 41 42 44 Pseudo Code radixsort(A, n) { for(i = 0; i < k; i++) { for(j = 0; j<si; j++) bin[j] = EMPTY;
- 63. 63 for(j = 0; j < n; j++) move Ai to the end of bin[Ai->fi] for(j = 0; j < si; j++) concatenate bin[j] onto the end of A; } } Complexity Worst case performance O(kN) Worst case space complexity O(kN) where k is the maximum number of digits. A variant of the Least Significant Digit radix sort is the Most Significant Digit (MSD) radix sort. It starts with the most significant digit. Merge Sort Merge Sort is a comparison-based sorting algorithm. Most of the used implementation produces a stable sort. The algorithm works as follows: • The unsorted input list is divided in two sub-lists of about half the size of the original • Each sub-list is sorted recursively by using again a merge sort • Afterwards the two sub-list are merge into one sorted list The basic idea behind the Merge Sort is that a smaller list takes less runtime than a bigger and fewer steps are necessary to construct a sorted list from two sorted lists than from an unsorted list. Example
- 64. 64 Figure 18 Merge Sort Algorithm #include <stdio.h> #include <stdlib.h> #define MAXARRAY 10 void mergesort(int a[], int low, int high); int main(void) { int array[MAXARRAY]; int i = 0; for(i = 0; i < MAXARRAY; i++) array[i] = rand() % 100; printf("Before :"); for(i = 0; i < MAXARRAY; i++) printf(" %d", array[i]); printf("n"); mergesort(array, 0, MAXARRAY - 1); printf("Mergesort :"); for(i = 0; i < MAXARRAY; i++) printf(" %d", array[i]); printf("n"); return 0; } void mergesort(int a[], int low, int high)
- 65. 65 { int i = 0; int length = high - low + 1; int pivot = 0; int merge1 = 0; int merge2 = 0; int working[length]; if(low == high) return; pivot = (low + high) / 2; mergesort(a, low, pivot); mergesort(a, pivot + 1, high); for(i = 0; i < length; i++) working[i] = a[low + i]; merge1 = 0; merge2 = pivot - low + 1; for(i = 0; i < length; i++) { if(merge2 <= high - low) if(merge1 <= pivot - low) if(working[merge1] > working[merge2]) a[i + low] = working[merge2++]; else a[i + low] = working[merge1++]; else a[i + low] = working[merge2++]; else a[i + low] = working[merge1++]; } } Output Before : 41 67 34 0 69 24 78 58 62 64 Mergesort : 0 24 34 41 58 62 64 67 69 78 Complexity Best case performance O(n log n) typical, O(n) natural variant Worst case performance O(n log n) Average case performance O(n log n)
- 66. 66 Bubble Sort The Bubble Sort is a simple sorting algorithm. It works by repeatedly stepping through a list of data. It compares each pair of elements and swapping them if they are in wrong order. This is done until no swap is needed any more. The name comes from the way smaller elements bubble to the top of the list. It is a comparison sort. The performance depends strongly on the position of the elements. If the smaller elements are stored at the end of the list the sort is extremely slowly. If the larger elements are at the beginning this cause no problem. They are therefore called turtles and rabbits. Example First round: 7 2 6 3 9 2 7 6 3 9 2 6 7 3 9 2 6 3 7 9 2 6 3 7 9 Second round: 2 6 3 7 9 2 6 3 7 9 2 3 6 7 9 2 3 6 7 9 2 3 6 7 9 Third round: 2 3 6 7 9 2 3 6 7 9 2 3 6 7 9 2 3 6 7 9 2 3 6 7 9 Algorithm void bubble(int a[],int n) { int i = 0, j = 0, t = 0; for(i = n-2; i >= 0; i--) { for(j = 0; j <= i; j++) { if(a[j] > a[j+1]) { t = a[j]; a[j] = a[j+1]; a[j+1] = t; } } } } Variants Variant of Bubble Sort Description Od-even sort Parallel version of bubble sort for message passing systems Cocktail sort Parallel version Right-to-left Instead of starting from the left side you start from the right side Table 4 Variants of Bubble Sort
- 67. 67 Complexity Best case performance O(n) Worst case performance O(n2 ) Average case performance O(n2 ) Comparing the algorithms Be n the number of records. In the table the discussed sorting algorithm are compared. For Average and Worst is assumed that all comparisons, swaps and other necessary operations can proceed in constant time. This table compares all comparison sorts. Name Best Average Worst Method Note Insertion sort O(n) O(n2 ) O(n2 ) Insertion Average also O(n + d) where d is the number of inversions Binary tree sort (later) O(n) O(nlogn) O(nlogn) Insertion using a self-balancing binary search tree Selection Sort O(n2 ) O(n2 ) O(n2 ) Selection Bubble Sort O(n) O(n2 ) O(n2 ) Exchanging Merge Sort O(nlogn) O(nlogn) O(nlogn) Merging Quick Sort O(nlogn) O(nlogn) O(n2 ) Partitioning Table 5 Comparing comparison sorts This table compares all sorting algorithm which are not comparison sorts. Be n the number of items, k the size of the key and d the digit implementation size. Name Best Average Worst Note Bucket Sort - O(n+k) O(n2 *k) uniform distribution of elements LSD Radix Sort - O(n*(k/d)) O(n*(k/d)) Table 6 Comparing other sorts
- 68. 68 Dynamic Data Structures Pointers Pointers are an essential instrument in dynamical data structures. But the use of pointers is not trivial. That is because of: • Technics working with pointer are hard to read • The changes for errors are higher. Especially undefined pointers are causing the most program crashes Address space When a program is executed the data are placed in the memory. You can see the memory as an array which elements are memory cells. The index area of this array is called address space. The single memory cell is in general a byte (8 bits). Each active program has its own virtual address space. In UNIX operating systems in the virtual address space first the program code is place followed by the global variables. The local variables and parameters are put in the stack. Directly below the global variable the dynamical data are allocated in the heap Figure 19 Address Space Dynamical Data If you need more memory during run time this memory is allocated in the free parts of the address space.
- 69. 69 In opposite to global variables the addresses of the memory locations are not constant. Therefore you need pointers. Pointers are variables whose values refers directly to (point to) another value by using its address. This address refers to a memory location in which the data are written. Therefore a pointer points to a memory address. p Figure 20 Pointer Example in C int *myptr = &myvar; More than one pointer can refer to the same memory location. In program language pointers are often used to realize a call-by-value function call, also for lists, strings, lookup tables, control tables and trees. You can still change the data behind the pointer. A pointer references a location in memory to obtain the value at this location is called dereferencing. In some program language the deallocation of the memory is done by a so called Garbage Collector (for example Java) but in other language the programmer has to take care of the deallocation by himself (for example C/C++). That leads to following problems: • The deallocation can be forgotten (memory leaks) • It is not always trivial to calculate what and when something has to be deallocated • Pointers are still used even when the deallocation has taken place (dangling reference). Leads to a mostly unexpected behavior of the program execution. Linear Lists To one of the simplest data structure belongs the Linear List. A number of elements ai are represented in an order form. a1 a2 … ai-1 ai ai+1 … an Typical operations are: • Putting a new element at the beginning or at the end of the list
- 70. 70 • Deleting an element from the list • Getting an element at position i (especially when i = 1 or i = n ) • Getting the next or previous element of an element ai (therefore ai+1 or ai-1) Examples for lists • Orders in a shop: Each element is equal to an order. The order tells which article has to be send to a costumer. Each new order is put at the end of the list. After finishing the order the element is deleted in the list. • Moves: Each element is equal to a move in a game. A new move is put at the end of the list. You can restore an old score by removing the last element • Timetable: Each element is equal to a new appointment or short information. All elements are sorted by time. New entries are therefore put in the list according to their time. Expired entries are deleted from the list. An implementation of a list data structure may require some of the following operations: • An operation to creating an empty list (init) • An operation to test whether or not a list is empty (isempty) • An operation for adding an entity to a list at the beginning • An operation for appending an entity to a list • An operation for receiving the first component element (head) of a list or the last element. • An operation for referring to the list consisting of all the components of a list except for its first (this is called the "tail" of the list.) Linked List A Linked List is a data structure that consists of a sequence of data records such that in each record there is a field that contains a reference (a link) to the next record in the sequence. Each record of a Linked List is often called an element or node. The field of each node that contains the address of the next node is usually called the next link or next pointer. The remaining fields are known as the data, information or value. Figure 21 Linked list
- 71. 71 Pseudo Code in C record Node { data; //The data being stored in the node Node next //A reference to the next node, null for last node } record List { Node firstNode //Points to first node of list; null for empty list } node = list.firstNode //Traversal from beginning to end while (node != null) { (do something with node.data) node = node.next } Insert a new node Figure 22 Insert a new node function insertAfter(Node node, Node newNode) { newNode.next = node.next node.next = newNode }
- 72. 72 Special case if you insert a new node at the beginning Figure 23 Insert Node at beginning function insertBeginning(List list, Node newNode) { newNode.next = list.firstNode list.firstNode = newNode } Removing a node Figure 24 Remove a Node
- 73. 73 function removeAfter(node node) { obsoleteNode = node.next node.next = node.next.next destroy obsoleteNode } function removeBeginning(List list) { obsoleteNode = list.firstNode list.firstNode = list.firstNode.next // point past deleted node destroy obsoleteNode } Circular List In the most cases the last node of a list contains a null value means that there is no next node in the list. In some cases a pointer to the first node of the list is made. This is called a Circular List. Figure 25 Circular List Insert an element at the beginning Figure 26 Circular List insert at beginning
- 74. 74 Pseudo Code in C void insert_at_beg(int num) { struct node *new_el; new_el = (node *)malloc(sizeof(struct node)); new_el->info = num; new_el->link = last->link; last->link = new_el; } Doubly-Linked List A Doubly-Linked List is a Linked List that contains a number of elements, each having two special fields referencing to the next and previous element in the list. You can view it as two Linked Lists formed from the same data items, in two opposite orders. Figure 27 Doubly-Linked Lists Pseudo Code in C record Node { data; // The data being stored in the node next; // A reference to the next node; null for last node prev; // A reference to the previous node; null for first node } record List { Node firstNode; // points to first node of list; Node lastNode; // points to last node of list; } Iterating through a Doubly Linked List can be done in either direction. In fact, direction can change many times, if desired. Forwards node = list.firstNode while (node != null) { //do something with node.data node = node.next; }
- 75. 75 Backwards node = list.lastNode while (node != null) { //do something with node.data node = node.prev; } Inserting a node Figure 28 Insert a Node in a Doubly Linked List
- 76. 76 Insert Code Example in C function insertAfter(List list, Node node, Node newNode) { newNode.prev = node; newNode.next = node.next; if (node.next == null) list.lastNode = newNode; else node.next.prev = newNode; node.next = newNode; } function insertBefore(List list, Node node, Node newNode) { newNode.prev = node.prev; newNode.next = node; if (node.prev == null) list.firstNode = newNode; else node.prev.next = newNode; node.prev = newNode; } function insertBeginning(List list, Node newNode) { if (list.firstNode == null) { list.firstNode = newNode; list.lastNode = newNode; newNode.prev = null; newNode.next = null; } else insertBefore(list, list.firstNode, newNode); } function insertEnd(List list, Node newNode) { if (list.lastNode == null) insertBeginning(list, newNode); else insertAfter(list, list.lastNode, newNode); }
- 77. 77 Removing a node Figure 29 Remove a node in a Doubly Link List Remove Code Example in C function remove(List list, Node node) { if (node.prev == null) list.firstNode = node.next; else node.prev.next = node.next; if (node.next == null) list.lastNode = node.prev; else node.next.prev = node.prev; destroy node; } Stack A Stack is also a Linear List with the significant that only at both ends elements could be added or removed. In a Stack you are mostly interested in the element on the top. Elements below are only appearing again if all elements on the top of it are removed. In computer science, a stack is a Last In, First Out (LIFO) abstract data type and data structure.
- 78. 78 Examples for Stacks Game Tic-Tac-Toe An implementation of a Stack may require some of the following operations: • An operation to creating an empty Stack (init) • An operation to add an element on the top of the Stack (push) • An operation to remove an element on the top of the Stack (pop) • An operation to receive the current element on the top of the Stack (top) • An operation to receive the length of the stack; the number of elements in the Stack (length) • An operation showing that the maximal capacity of the Stack is reached (full) In the most program language the implementation of Stack can be done with arrays. The C++ Standard Template Library provides a Stack Template Class which is restricted to only push/pop operations. Java's library contains a Stack class that is a specialization of Vector. Example implementation in C The Stack is realized by using an array in a structure which additional information about the size of the Stack. typedef struct { int size; int items[STACKSIZE]; } STACK; void push(STACK *ps, int x) { if (ps->size++ == STACKSIZE) { fputs("Error: stack overflown", stderr); abort(); } else ps->items[ps->size++] = x; } int pop(STACK *ps) { if (ps->size == 0) { fputs("Error: stack underflown", stderr); abort(); } else return ps->items[--ps->size];
- 79. 79 } You can also realize the Stack implementation by using pointers. Queues A Queue or FIFO (First-In-First-Out) is a Linear List where at one end elements are added and on the other end elements are removed. The inner elements are not considered. The elements will be processed in exactly the same order in which they are original placed. The following operations exists in general for queues • init() initialize an empty queue. • isempty() true if the queue is empty • pop() removes the item at the front of the queue • push() insert an item at the back of the queue • size() return the number of elements in the queue • front() returns a reference to the value at the front of a non-empty queue The C++ Standard Template Library provides a Queue Template Class. Example in C #include <stdio.h> #define QMAX 100 int Queue[QMAX]; int qLast = 0; void printqueue() { printf ("Queue: "); for (int i = 0; i < qLast; i++) printf ("%i ", Queue[i]); printf ("n"); } void enqueue(int qItem)
- 80. 80 { Queue[qLast] = qItem; qLast++; printqueue(); } int dequeue() { int qReturn = Queue[0]; for (int i = 0; i < qLast - 1; i++) Queue[i] = Queue[i + 1]; qLast--; printqueue(); return (qReturn); } int main() { for (int i = 0; i < 10; i++) enqueue(i); printf("%dn", dequeue()); return 0; } Sorted List In a Sorted List each element has a key. For this key a complete order relation ≤ exists with: a ≤ a (reflexivity) a ≤ b and b ≤ a a = b (anti symmetry) a ≤ b and b ≤ c a ≤ c (transitivity) The following operations exist for Sorted List: • init() initialize an empty Sorted List • insert() insert an element in the list so that the Sorted List is still sorted • removefirst() removes the first element in the list (the element with the lowest key) • getfirst() get the first element from the Sorted List • search(key) search for an element with given key • delete(key) delete an element with given key • length() the size of the Sorted List
- 81. 81 Insert in a Sorted List Different from other list variants the value of the new element decided in which place of the list it will be insert. If the list is empty or if the value of the first element is greater than the value of the new element, the new element is to be inserted at beginning of the list. Otherwise you have to pass through the list until you find a value greater than the value of the new element. For this you use a pointer passing from element to element and comparing the values. Traversing is also necessary if you print out an element or if you remove an element of the list. Linked Lists vs. Dynamic Arrays Linked list Array Dynamic array Indexing Θ(n) Θ(1) Θ(1) Insertion/deletion at beginning Θ(1) N/A Θ(n) Insertion/deletion at end Θ(1) N/A Θ(1) Insertion/deletion in middle search time + Θ(1) N/A Θ(n) Wasted space (average) Θ(n) 0 Θ(n) Figure 30 Comparing linked list/dynamic arrays from Wikipedia.org Tree structures General Trees are one of the most important data structures. There are several different variants. We will have a closer look to some of them. Definition A Tree is a finite amount T of one or several nodes such that • There is a significant node called root(T) • The other nodes can be divided in disjunctive amount T1, .. Tm. Each of these amounts is again a Tree. These Trees are called Sub Trees. This is a recursive definition. At the end a Tree with only one node remains.
- 82. 82 Definitions for Trees • Each node in a Tree is the root of one of the Sub Trees. • Each Tree has zero or more child nodes which are below in the Tree. • A node with a child node is called parent node to the child (also ancestor node or superior). • The root node is the Tree with no parents. Each Tree has at least one root node. • The height of a Tree is the length of the path from the root to the deepest node in the Tree: h(T) = 0 if the Tree T is empty h(T) = max(h(T1), h(T2)) + 1 where T1 is the left and T2 the right Sub Tree • The depth of a node is the length of the path to its root. • A node p is an ancestor to node q if p exists on the path from q to root. The node q is called a descendant of p. • The size of a node is the number of descendants a node has including itself. • Siblings are nodes that share the same parent node. • Nodes without a child node are called leaf node or terminal nodes. • Internal or inner node are nodes with one or more child nodes therefore height > 0 • In-degree of a node is the number of edges arriving at that node. The only node with In-degree = 0 is the root node. • Out-degree of a node is the number of edges leaving that node • The level of a node is defined as: o The level of the root(T) is 0. o The level of any other node is increased by 1 to the level of the node which is the root of the superior sub tree. Figure 31 Level of a Tree Balanced Trees If the relative order of the Sub Trees is important you call it a Balanced Tree. If the order is not important this is called an Oriented Tree.
- 83. 83 Example These Trees are different if you look at them as Balanced Tree but they are consider as the same if you look at them as Oriented Trees. Figure 32 Balance Tree vs. Oriented Tree Tree Representation You can display Trees in different ways. In this course outline Trees are illustrated with the root on the top and the Sub Trees below. This is a common illustration. These are some different representations. Figure 33 Tree Representation
- 84. 84 Family Trees Two variants of Family Trees exist: • Starting from an ancestor as root and illustrated all the descendants • Starting from a descendant as root and illustrated all the ancestors In Family Trees you can have redundancies if some of the ancestors have the same ancestors. In this case the entries represent the role of the ancestor (for example grandmother on the mother’s side). Figure 34 Family Tree Noah and Prince Charles Binary Trees A Binary Tree is a finite amount of nodes where the amount is empty or contains a root and two disjunctive Binary Trees. These two Binary Trees are called left and right Sub Tree of the root. Binary Trees are not a special case of Trees in general. For example you can have an empty amount as a Binary Tree but not as a General Tree.
- 85. 85 Any data in the Tree structure can be reached by starting at the rood node and following either the left or the right child. Binary Trees are used for implementation of Binary Tree Search and Binary Heaps. Examples for Binary Trees are the elimination contest in tennis or other sport competitions. Example These two Binary Trees are not the same. One has left and the other a right Sub Tree. Figure 35 Binary Tree Implementation Binary Trees are easily implemented as a data type like • One pointer points to the root. If this pointer is null than the Tree is empty • A node in the Binary Tree contains a pointer to an object or a record and the two pointers to the left and the right Sub Tree Figure 36 Binary Tree
- 86. 86 There are three possibilities to traverse a Binary Tree: • preorder • inorder • postorder If the Tree is empty there is nothing to do. Otherwise the traverse possibilities are defined as: preorder visit the root traverse the left sub tree traverse the right sub tree inorder traverse the left sub tree visit the root traverse the right sub tree postorder traverse the left sub tree traverse the right sub tree visit the root void TraverseInorder(node * tree) { if(tree->left) TraverseInorder(tree->left); printf("%dn",tree->val); //or visit(tree); if(tree->right) TraverseInorder(tree->right); } Examples Figure 37 Binary Tree Example
- 87. 87 preorder: A B D C E G F H I inorder: D B A E G C H F I postorder: D B G E H I F C A Also mathematical formulas can be represented by Binary Trees: Figure 38 Mathematical Formulas as Binary Tree preorder: - * * + 4 2 7 + 9 3 / 8 – 4 inorder: 4 2 + 7 * 9 3 + * 8 4 - / - postorder: 4 + 2 * 7 * 9 + 3 - 8/- 4 (adding parentheses): (4 + 2) * 7 * (9 + 3) – (8/(-4)) The preorder traverse is also called Polish notation (after the Polish logician Jan Lukasiewicz) and the postorder traverse is therefore called a backwards Polish notation. Sorted Binary Tree A tuple (T, v, V, R) is a Sorted Binary Tree where v: T V, R order relation for V x V, T a Binary Tree and T1 the left Sub Tree and T2 the right Sub Tree and T1 and T2 are also Sorted Binary Trees such that: v(root(T)) > R v(t) for all t ϵ T1 v(root(T)) ≤ R v(t) for all t ϵ T2 If you traverse a Sorted Binary Tree inorder, than all values are reached in a sorted way.
- 88. 88 Figure 39 Inorder Traverse: 1 3 5 6 7 8 9 Definition The cardinality of a Tree T is the number n of elements in the Tree that means: n = card(T) A Tree is called height-balancing if the Tree T is empty or if | h(T1) – h (T2) | ≤ 1 where h is the height of a Tree and also the Sub Trees T1 and T2 are height-balancing Trees A Tree is called balanced if the Tree T is empty or if | card(T1) – card(T2) | ≤ 1 and also the Sub Trees T1 and T2 are balanced. If a Tree T is balance he is also balanced in its height.
- 89. 89 Examples Figure 40 Balanced in heights but not balanced and a balanced Tree Binary Search Tree Be k ϵ V (Values) a value and the search element be t ϵ T (Binary Tree) such that v(t) = k: • If T is empty than there is nothing to do • Be t = root(T). If v(t) = k than the search element is found • If not than o T = T1 if k < v(t) and o T = T2 if k ≥ v(t) where T1 be the left sub tree and T2 the right sub tree. The effort for the search is O(h(T)). Insert a element in a Sorted Binary Tree Be u ϵ V (values) with k = v(u) to be insert in the tree T. • Create a new binary sorted tree U containing only the root u • If T is empty replace T by U • Otherwise o T = T1 if k < v(u) and o T = T2 if k ≥ v(u) The effort is also O(h(T))
- 90. 90 Example Insert in an empty Tree the elements 5, 1, 3, 2, 8, 4, 6, 7 and 9: Figure 41 Insert in a Sorted Binary Tree Delete a node in a Sorted Binary Tree Be u ϵ T the node to be removed from T. Be U the sub tree from T with root(U) = u. • If the left Sub Tree U1 of U is empty than replace U by U2 • If the right Sub Tree U2 of U is empty than replace U by U2 • If both Sub Trees are not empty than: o Chose an u2 ϵ U2 such that v(u2) ≤ v(t) for all t ϵ U2 o u2 has to be removed from U2 o u2 replace the node u The effort to delete a node in a Tree is O(h(T)) due to the search for the minimal element u2.
- 91. 91 Example Figure 42 Remove a node in a Sorted Binary Tree Looking for the next element in a Sorted Binary Tree: Be k ϵ V search for a node n(T, k) = n ϵ T with v(u) > k and exist an u’ ϵ T: v(u’) > k and v(u’) < v(u). • If T is empty there is no such element • Be t = root(T). o If k ≥ v(t) than is n(T2, k) the searched element (if exist) o If k < v(t) than is n(T1, k) the search element (if exist) or t Other Tree Types • 2-3 tree • 2-3-4 tree • AA tree • AVL tree • B-tree • Elastic binary tree • Random binary tree • Red-black tree • Self-balancing binary search tree • Unrooted binary tree Example Implementation in C #include <stdio.h>
- 92. 92 #include <stdlib.h> struct btreenode { struct btreenode *leftchild ; int data ; struct btreenode *rightchild ; }; void insert(struct btreenode **sr, int num); void inorder(struct btreenode *sr); void main() { struct btreenode *bt = NULL; int arr[10] = {11, 2, 9, 13, 57, 25, 17, 1, 90, 3}; int i = 0; printf("Binary tree sort.n"); printf("nArray:n"); for(i = 0; i <= 9; i++) printf ("%dt", arr[i]); for (i = 0; i <= 9; i++) insert (&bt, arr[i]); printf ("nIn-order traversal of binary tree:n"); inorder(bt); } void insert(struct btreenode **sr, int num) { if (*sr == NULL) { *sr = (btreenode *)malloc(sizeof(struct btreenode)); (*sr)->leftchild = NULL; (*sr)->data = num; (*sr)->rightchild = NULL; } else { if (num < (*sr)->data) insert(&((*sr)->leftchild), num); else insert(&((*sr)->rightchild), num); } } void inorder(struct btreenode *sr) { if (sr != NULL) { inorder(sr->leftchild); printf("%dt", sr->data);
- 93. 93 inorder(sr->rightchild); } } Output Binary tree sort. Array: 11 2 9 13 57 25 17 1 90 3 In-order traversal of binary tree: 1 2 3 9 11 13 17 25 57 90
- 94. 94 References & Links • N.Wirth, “Algorithms and Data Structures”,Oberon version, 2004 • Andreas Franz Borchert, “Allgemeine Informatik II”, Universität Ulm, 1999 • http://www.webopedia.com/TERM/D/data_type.html • http://wikieducator.org/DATA_REPRESENTATION_IN_COMPUTER • http://alienryderflex.com/quicksort/ • http://en.wikibooks.org/wiki/Algorithm_implementation/Sorting/Quicksort • http://www.c.happycodings.com/Data_Structures














![15
Complex data types
Other data types are complex data type consists of standard data types.
Array
An array consists of elements of the same type (base type). An array has therefore a homogeneous
structure and is a random-access structure that means all elements can be selected at random and they
are equally accessible. To denote an element of an array is approached by the index. The index is an
integer between 0 and n-1 when the array contains n element. n is called the size of the array.
data_type array_name[n]
TYPE array_name = ARRAY n OF data_type
To access an element of the array using the index i:
array_name[i]
Example
TYPE column = ARRAY 5 OF INTEGER
int column[5];
TYPE NAME = ARRAY 32 OF CHAR
char name[32];
Note
Elements of an array are mostly selectively updated. The fact that the index is an integer has a most
important consequence: indices can be computed. On the one side this generality provides a most
powerful programming facility but on the other side is also gives rise to one of the most encountered
programming mistakes: The calculate indices might be out of the range of the array.
Example Implementation in C
Finding the sum and max of an array implemented in C:
int arr[n];
int sum = 0;
for (i = 0; i < n; i++)
sum = sum + arr[i];
int k = 0;](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-15-320.jpg)
![16
int max = arr[0];
for (i = 1; i < n; i++)
{
if (max < arr[i])
{
k = i;
max = arr[k];
}
}
Matrix
A matrix is an array whose elements are again arrays. Selectors may be concatenated accordingly, such
that Mij or M[i][j] denote the jth
component of row Mi, which is the ith
component of M. This is usually
abbreviated as M[i, j].
Example
int matrix[4][3]; This is 4x3 matrix
Vectors
Vectors are much like arrays. Operations have the same effort as their counterparts on an array. Like
arrays, vector data is allocated in contiguous memory.
Unlike arrays vectors have no fixed size. They can grow. This can be done by adding more data or
demand for it explicitly. In order to do this efficiently, the typical vector implementation grows by
doubling its allocated space and has therefore often more space allocated than it needs because
reallocating memory can sometimes be an expensive operation.
Some programming languages offer a data type vector (Standard Template Library (STL) in C++, Java). It
functions like a dynamic array.
Records/Structures
A structure or record data type is a join of elements of arbitrary types to a compound. In mathematics
we have the example of the complex numbers composed of two real numbers or points in a coordinate
system. Another example is a structure of data describing a person (first and last name, birthdate, sex,
etc.)](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-16-320.jpg)
![17
Definition
A complex number is a number composed of a real and imaginary part. It can be written as:
a + bi,
where a and b are real numbers, i is the standard imaginary unit with i2
= −1.
In mathematics such a compound type is the Cartesian product of its constituent types. The set of values
defined by this compound type consists of all possible combinations of values, taken one from each set
defined by each constituent type. The number of such combinations is also called n-tuples. It is the
product of the number of elements in each constituent set.
In data processing, composite types, such as descriptions of persons or objects, usually occur in files or
data banks and record the relevant characteristics of a person or object. The word record (instead of
Cartesian product) is widely accepted to describe a compound of data of this nature.
A record or structure type R with components of types R1, R2 … Rn is defined as
struct struct_name
{
r1: R1;
r2: R2;
…
rn: Rn;
} ;
card (struct) = card(R1) * card(R2)*…*card(Rn)
A component of a record is called field and the name is called field identifier.
Example
struct Date
{
int day;
int month;
int year;
};
struct Person
{
char name[32];](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-17-320.jpg)
![18
char firstname[32];
Date birthdate;
};
struct Complex
{
float re;
float im;
};
Example
Be p a Person than:
p.name is from type Char
p.birthdate is from type Date
p.birthdate.day is from type Integer
Node
It is a characteristic of the Cartesian product that it contains all combinations of elements of the
constituent types. But in practical applications not all of them are valid. For example the type Date
includes the 35th
May as well as the 31st
November, dates which are not valid. It is in the responsibility of
the programmer to make sure that invalid values not occur during execution of the program.
Representation of Data in the Computer
The data in Computer Systems are presented through a binary or two's complement numbering system.
Bit
A bit or binary digit is the smallest unit of data in computing. A bit representing only two different value
interpreted by 0 and 1. But you can represent an infinite number of items with only one bit (true/false,
red/blue, male/female, +/-, on/off) because the data are what you define them to be.
Nibbles
A collection of 4 bits is called nibble. Nibbles represent binary coded decimal (BCD) and hexadecimal
number. You can display up to 16 distinct values. For hexadecimal number and BCD four bits are
required for the representation.](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-18-320.jpg)





![24
Searching Methods
Many different algorithms have been developed on searching methods.
We assume that you search for a given element in a set of N elements represented as an array. The type
item has a record structure with a field acting as a key. The task is to find an element x whose key field is
equal to a given search element x. The result has index i so that:
a[i].key = x
Linear Search
Linear search is to proceed sequentially through the array until the element you searched for is found.
There are two conditions terminating the search:
1. The element is found that mean a[i].key = x
2. The element is not found in the array that means there was no element with a[i].key = x
Example Algorithm
int i = 0;
while ((i < n) && (a[i] != x))
{
i++;
}
It terminates when (i = N) or (a[i] = x). In this case the order of the condition is relevant. If i = N than no
match exists. Because i is increased the repetition will reach an ending.
You can alter the algorithm by using an additional element at the end of the array with value x. This
element is called sentinel. Our array has therefore now N+1 elements with a[N] = x;
Example Algorithm
a[N] = x;
i = 0;
while (a[i] != x))
{
i++;
}](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-24-320.jpg)
![25
It terminates when a[i] = x. If i = N that implies no match has found (beside the sentinel).
Binary Search
To speed up a search you need more information about the search data. If the data are ordered the
search is much more effective. For example in a telephone book the data are alphabetically ordered.
Assuming our data are order such that
a[k-1] ≤ a[k] where 1 ≤ k ≤ N
The algorithm based on:
• if you pick an element a[i] at random and compare it with the search element than the search
terminates if they are equal
• if it is less than the search element than all elements with indices less or equal to i can be
eliminated from the search
• if it is greater than the search element than all elements with indices greater or equal to i can be
eliminated
This is called binary search. Be L the left and R the right end indices of the section in which elements still
can be found.
Algorithm
L = 0;
R = N – 1;
found = false;
while ((L ≤ R) && !found)
{
i = ”any value between L and R”;
if (a[i] = x)
found = true;
else if (a[i] < x)
L = i + 1;
else
R = i – 1;
}
The repetition ends when found is true or ((L > R) & (a[k] < x; 0 ≤ k < L) & (a[k] > x; R < k < N) which
implies (a[i] = x) or (a[k] ≠ x; 0 ≤ k < N)](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-25-320.jpg)
![26
The correctness of this algorithm does not depend on the chosen i but it does influence the
effectiveness. You wish to eliminate as much elements as possible in each step. The optimal solution is to
choose the middle element. This eliminates half of the array in any case. As a result the maximal number
of step is log2N. For linear searches the number of comparisons to be expected is N/2.
Example
N = 1024 linear search: 612
binary search: 10
The algorithm can be also improved by chancing the second if clauses because if you test the equality as
a second step it occurs only once and causes termination.
Another improvement can be made if you chance the algorithm to:
L = 0;
R = N;
while (L < R)
{
i = (L + R) / 2;
if (a[i] < x)
L = i + 1
else
R = i;
}
The repetitions ends when L ≥ R. In each step L will be increased or R will be decreased and it ends when
L = R. In contrast to the first solution this algorithm finds the matching element with the last index.
Example
Array a = {1, 4, 6, 9, 10, 15, 18, 23, 27, 34, 44}
Searching for x = 27
L = 0 and R = 11 = N
First Round: i = 11/2 = 5
a[i = 5] =15 < x = 27 L = 6 and R = 11
Second Round: i = 17/2 = 8
a[i = 8] = 27 = x L = 6 and R = 8
Third Round: i = (6+8)/2 = 7
a[i = 7] = 23 < x = 27 L = 8 and R = 8
Index = R = L = 8](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-26-320.jpg)
![27
Table Search
A search through an array is sometimes called a table search. This is particularly the case if the elements
of the array are themselves structured object like numbers of characters.
Definition
An array of characters is also called a string.
• Equality of strings is defined by: s = t ≡ (si = ti; 0 ≤ i ≤ N)
• An order of strings is defined by: s < t ≡ (si = ti) & (sj < tj); 0 ≤ i ≤ j and 0 ≤ j < N
To find a match between strings all characters have to be equal. This comparison can also be seen as a
search of an unequal pair that means a search for inequality. If no unequal pairs exist the strings are
equal. If the length of the strings is small a linear search can be used.
The length of a string can be represented as:
• A string is terminated by a specific terminating character. In the most cases the null character0
is used.
• The length is stored at the first element of the array. Therefore the string s is represented as
s = s0, s1, s2… sN-1
where s0 is the length = CHR(N) and s1, …, sN-1 are the characters of the string.
In this solution the length is directly available.
Algorithm
i = 0;
while ((s[i] == t[i]) && (s[i] != ‘0’))
{
i++;
}
In this case the termination character 0 functions as a sentinel.
The table search needs a nested search that means a search through the entries of the table and for each
entry a sequence of comparisons between components. Be T a table of strings and s the search
argument and N a large number and may the table be alphabetically ordered. Than we use a binary
search.](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-27-320.jpg)
![28
Algorithm
L = 0;
R = N;
while (L < R)
{
i = (L + R) / 2;
j = 0;
while (T[i][j] = s[j]) & (s[j] != ‘0’)
{
j++;
}
if (T[i][j] < s[j])
L = i + 1;
else
R = i;
}
Example
Table T = {Valarie, Valentine, Vance, Vanessa, Vaughn, Velma, Vera, Verity, Verna, Vernon,
Veronica, Vicky, Victor, Victoria, Vincent, Viola, Violet, Vivian}
Search string s = Victor
L = 0, R = 18;
First Round i = (0 + 18) / 2 = 9, j = 0
while T[9][0] = V = s[0] = V j = 1
T[9][1] = e != s[1] = i
if L = 9 + 1 = 10
Second Round i = (10 + 18)/2 = 14, j = 0
while T[14][0] = V = s[0] = V j = 1
T[14][1] = i = s[1] = i j = 2
T[14][2] = n != s[2] = c
if R = 14
Third Round i = (10 + 14)/2 = 12, j = 0
while T[12][0] = V = s[0] = V j = 1
T[12][1] = i = s[1] = i j = 2
T[12][2] = c = s[2] = c j = 3
T[12][3] = t = s[3] = t j = 4
T[12][4] = o = s[4] = o j = 5
T[12][5] = r = s[5] = r j = 6
if R = 12
Fourth Round i = (10 + 12)/2 = 11, j = 0
while T[11][0] = V = s[0] = V j = 1](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-28-320.jpg)
![29
T[12][1] = i = s[1] = i j = 2
T[12][2] = c = s[2] = c j = 3
T[12][3] = k != s[3] = t j = 4
if L = 10 + 1 = 11
Fifth Round i = (11 + 12)/2 = 11, j = 0
while T[11][0] = V = s[0] = V j = 1
T[12][1] = i = s[1] = i j = 2
T[12][2] = c = s[2] = c j = 3
T[12][3] = k != s[3] = t j = 4
if L = 10 + 1 = 12
R = L = 12
Straight String Search
A string search is to find an array in another array. Typically the elements of the arrays are characters.
Than you can regard the one array as a text and the searching array as a pattern or word you wish to find
in the text. In the most cases you look for the first appearance of the word in the text.
The straight string search is a straightforward searching algorithm for this task.
Definition
Be s an array of N element and p an array of M element where 0 < M < N. Let i be the result index of the
first occurrence of the searching array p in an array s than a predicate P is defined as:
P(i, j): si+k = pk with 0 ≤ k < j.
Because the first occurrence of the pattern is searched P(k, M) must be false for all k < i. Therefore you
can define a condition Q(i) like
Q(i) = ~P(k, M) with 0 ≤ k < i
The search is formulated as an iteration of comparisons like
i = -1;
do
{
i++;
found = P[i][M];
}
while (!found && i != N - M);](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-29-320.jpg)
![30
The best way is that the iteration for P is a search for inequality among the corresponding pattern and
string characters. This leads to a Pseudo algorithm like:
i = -1;
do
{
i++;
j = 0;
while ((j < M)&& (s[i+j] == p[j])
{
/*P[i][j+1]; //handling with the pattern
j++;
}
}
while (j != M && i != N - M);
The term i = N – M implies the nonexistence of a match anywhere in the string.
Other string searches
• Knuth-Morris-Pratt String Search
• The Boyer-Moore String Search](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-30-320.jpg)






![37
This is especially the case for tail recursion which can be replaced immediately by a loop, because no
nested case exists which has to be represented by a recursion. The recursive call happens only at the end
of the algorithm.
Recursion and iteration are not really contrasts because every recursion can also be implemented as
iteration.
There are two ways to implement a recursion:
• Starting from an initial state and deriving new states which every use of the recursion rules.
• Starting from a complex state and simplifying successive through using the recursion rules until a
trivial state is reached which needs no use of recursion.
How to build a recursion depends mainly on:
• How readable and understandable the alternative variants are
• Performance and memory issues
Tail recursion
int tail_recursion(…)
{
if (simple_case)
/*do something */;
else
/*do something */;
tail_recursion(…);
}
Example
The faculty algorithm is more efficient if you use an iterative implementation
int faculty(int number)
{
int result = 1;
while (number > 0)
{
result *= number;
number--;
]
return number;
}](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-37-320.jpg)

![39
Peano-Hilbert curve
Figure 6 Peano-Hilbert Curve
The Peano-Hilbert curves were discovered by Peano and Hilbert in 1890/1891. They convert against a
function. This function map the interval [0,1] of the real numbers surjective on the area [0,1] x [0,1] and
is in the same time constant.
The Peano-Hilbert Curve can be expressed by a rewrite system (L-system).
Alphabet: L, R
Constants: F, +, −
Axiom: L
Production rules:
L → +RF−LFL−FR+
R → −LF+RFR+FL−
F: draw forward
+: turn left 90°
-: turn right 90°
Implementation in C
#include <stdio.h>
#include <stdlib.h>
void f(int x, int y, int m)
{
x = m - abs(m-x);
if (x == m || y == m )
{
putchar(x == 0 || y == m+1 ? '@' : ' ');
}
else
{
if (y>m)
f(x, y&m, m/2);
else](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-39-320.jpg)





![45
void permutation(char list[], int start, int max)
{
int i;
if(start == max)
{
for(i = 0; i < SIZE; i++)
printf("%c", list[i]);
printf("n");
}
else
{
for(i = start; i < max; i++)
{
swap(list[i], list[max - 1]);
permutation(list, start, max - 1);
swap(list[max - 1], list[i]);
}
}
}
int main()
{
char my_list[5] = {'a','b','c','d','e'};
permutation(my_list, 0, SIZE);
return(0);
}
Problem
Generate all possible permutation out of n object.
Solution
Two solution methods exist for this problem:
Method1
For each permutation a1 a2 … an-1 you generate n new ones by putting the number n at all
possible places: n a1 a2 … an-1 a1 n a2 …. an-1 …. a1 a2 … an-1 n
Method2
For each permutation a1 a2 … an-1 an integer k with 1 ≤ k ≤ n is added an each ai is increased by 1
if ai ≥ k.](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-45-320.jpg)


![48
Figure 12 n-queen problem with n = 4
There are 16!/12! = 43 680 possibilities to set 4 queens on a 4x4 chessboard.
If you consider only the k row for the queen k than the number of possibilities is reduced to nn
. In this
case: 44
= 256.
If you threw away all position where even less then n queens threaten each other than you have only 17
possibilities left.
Under these possibilities there are only 2 solutions and 4 death ends.
Example implementation in C
# include <stdio.h>
# include <stdlib.h>
# include <time.h>
int flag;
int number_of_queens = 0;
void printArray(int arr[]);](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-48-320.jpg)
![49
void getPositions(int arr[], int n1, int n2);
int main()
{
int *arr_queen;
int iterator = 0;
printf("-----------------------n-Queens Problem-------------------
--n");
printf("Please enter the number of rows(n) for the nxn chessboard:
n");
scanf("%d", &number_of_queens);
arr_queen = (int *)(malloc(sizeof(int)*number_of_queens));
printf("The rows and columns are numbered from 1 to n and the
given solution has form (row, col).n");
printf("All possible solutions are: n");
for(iterator = 0; iterator < number_of_queens; iterator++)
getPositions(arr_queen, 0, iterator);
getchar();
}
void printArray(int arr[])
{
int i = 0;
static int counter = 0;
counter++;
printf("Solution: # %d: ", counter);
for(i = 0; i < number_of_queens; i++)
printf("(%d, %d) ", i + 1, arr[i] + 1);
printf("n");
}
void getPositions(int arr[], int colno, int val)
{
int iterator1 = 0, iterator2 = 0;
arr[colno] = val;
if(colno == number_of_queens - 1)
{
printArray(arr);
return;
}
for(iterator1 = 0; iterator1 < number_of_queens;)
{
for(iterator2 = 0; iterator2 <= colno; iterator2++)
if(arr[iterator2] == iterator1 ||](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-49-320.jpg)
![50
(colno + 1 - iterator2)*(colno + 1 - iterator2)
== (iterator1 - arr[iterator2])*(iterator1 -
arr[iterator2]))
goto miss1;
getPositions(arr, colno + 1, iterator1);
miss1:
iterator1++;
}
}
Output
Please enter the number of rows (n) for the nxn chessboard:
4
The rows and columns are numbered from 1 to n and the given solution has form (row, col).
All possible solutions are:
Solution: # 1: (1, 2) (2, 4) (3, 1) (4, 3)
Solution: # 2: (1, 3) (2, 1) (3, 4) (4, 2)
Chose the data structure
The efficiency of the backtracking algorithm depends strongly on the chosen data structure.
How efficient is
• The check if a solution is reached
• The identification of possible steps in a given situation
• The check of the usefulness of a part solution
• The execution of a step
If possible each step should have an effort of O(1).
You can improve for example the implementation of the n-queen problem if you save the amount of
threaten row, columns and diagonals.
Travelling Salesman
Another problem is the travelling salesman.
Description
• Be n a number of place in a n x n distance matrix M where Mi,j is the distance between the places
i and j.
• Seek for the route with the minimal length such that all places are reached exactly one time and
then return to the starting point.](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-50-320.jpg)




![55
A sorting problem must not be numerical it must be only be distinguishable (e.g. by colors, by size).
Therefore it must be possible for a sorting algorithm to decide if an element of the set is smaller than
another element. For example you can make a numbered list for colors. In numerical values the compiler
automatically knows how to treat them. For characters you can use for example the ASCII table to decide
how the sorting is done.
All the algorithms now discussed work with numerical representations where a smaller-, bigger-, same-
relation is defined.
Indirect Sort
If you keep a list with references to a record the necessary time for swapping the data in the record can
be drastically reduced. Afterwards the record is still untouched. But the array with references helps to
rearrange the data in the record. The necessary time increases in linear fashion with the number of data
in the record. This is called Indirect Sort.
Definition
Be A an array, n the number of elements in the array. Than an auxiliary array P is defined by P[i] = i for all
i = 1, 2 …, n and the objective is to modify P so that
A[P[1]] ≤ A[P[2]] ≤ … ≤ A[P[n]]
Therefore instead of change the array A we change the array P.
An Indirect Sort is indicated when the costs for swapping the data is high and the additional memory
cause no problem.
Distribution Sort
A sorting algorithm is called a Distribution Sort if the data is distributed from its input to a multiple
temporary structure. This structure is collected and placed on the output.
Stable Sorting
For some data you wish to sort them by more than one criterion. For example in a list of address you sort
first by the last name and the last names by the first names. A sorting algorithm is called stable when](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-55-320.jpg)

![57
sorted part unsorted data
≤ s >s s …
≤ s s >s …
Figure 15 Insertion Sort
Algorithm
#include "stdio.h"
void sort(int arr[])
{
int i = 0, j = 0, k = 0, temp = 0;
for (i = 1; i < 5; i++)
{
for (j = 0; j < i; j++)
{
if (arr[j] > arr[i])
{
temp = arr[j];
arr[j] = arr[i];
for (k = i; k > j; k--)
arr[k] = arr[k - 1];
arr[k + 1] = temp;
}
}
}
}
void main( )
{
int arr[5] = {25, 17, 31, 13, 2};
int i = 0;
printf ("Insertion sortn");
printf ("Array before sorting:n");
for (i = 0; i < 5; i++)
printf ("%dt", arr[i]);
sort(arr);
printf("nArray after sorting:n");
for (i = 0; i <= 4; i++)
printf ("%dt", arr[i]);
}](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-57-320.jpg)

![59
<pivot pivot >pivot
<pivot’ pivot’ >pivot’ pivot <pivot’’ pivot’’ >pivot’’
Figure 16 Quick Sort
Example Algorithm
void swap(int *a, int *b)
{
int t = *a;
*a = *b;
*b = t;
}
void sort(int arr[], int beg, int end)
{
if (end > beg + 1)
{
int piv = arr[beg];
int l = beg + 1;
int r = end;
while (l < r)
{
if (arr[l] <= piv)
l++;
else
swap(&arr[l], &arr[--r]);
}
swap(&arr[--l], &arr[beg]);
sort(arr, beg, l);
sort(arr, r, end);
}
}
Simple Algorithm
quicksort( void *a, int low, int high )
{
int pivot;
if ( high > low )
{
pivot = partition(a, low, high);
quicksort(a, low, pivot-1);
quicksort(a, pivot+1, high);
}](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-59-320.jpg)

![61
put (array[i], buckets[msbits(array[i], k)];
for (int j = 0; j < n; j++)
next-sort(buckets[j]
return concat(buckets[0] , buckets[1], …, buckets[n-1])
msbits(x, k) returns the k most significant bits of x. Of course different functions can be used to arrange
the element in the buckets.
Example
33, 41, 22, 8, 4, 12, 19, 37, 45, 7, 17, 26, 29, 34
Bucket 0-9 Bucket 10-19 Bucket 20-29 Bucket 30-39 Bucket 40-49
Variants of Buckets Sort are
Name Description
Generic bucket sort operates on a list of n numeric inputs between 0 and a maximum value Max and
divided the value range into n buckets with size Max/n.
Proxmap sort operates by dividing an array of keys into buckets and sorting the data than by
using a mapkey function to characterize the data
Histogram sort operates by adding an initial pass that counts the number of elements that will be
put in each bucket using a count array. This information can be used to arrange
the array values into a sequence of buckets in-place by a sequence of exchanges
avoiding space overhead for bucket storage
Postman’s sort operates on hierarchical structure elements. It is used by letter-sorting machines.
Mail is sorted first between nation and international, then state, province,
district, city, streets/routes, etc. The keys are not sorted against each other. Time
is O(cn) where c depend on the size of the key and number of buckets.
Shuffle sort operates by removing the first 1/8 of the elements n, sorts them recursively and
puts them in an array. It creates n/8 buckets to which the remaining 7/8
elements are distributed. Each bucket is sorted and concatenated into a sorted
array
Table 3 Variants of Bucket Sort
8
4
7
12
19
17
22
26
29
33
37
34
41
45
Figure 17 Bucket Sort Example](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-61-320.jpg)
![62
Radix Sort
A very old sorting algorithm (invented 1887 by Herman Hollerith) is the Radix Sort. The Radix sort was
used to sort cards. In general it sorts integers but it is not limited to it (e.g. characters can be represented
by numbers).
The algorithm distributes items to a bucket according to the item’s key part beginning with the least
significant part of the key. After each round the items are recollected from the buckets. The process is
repeated with the next most significant part of the key and so on. This is called Least Significant Digit
Radix Sort (LSD).
Example
Input keys: 34, 12, 42, 32, 44, 41, 34, 11, 32, 23
4 buckets, because 4 different digit 1, 2, 3, 4
Sorting by the least significant digit:
1. Bucket: 41 11
2. Bucket: 12 42 32 32
3. Bucket: 23
4. Bucket: 34, 44, 34
Recollecting: 41 11 12 42 32 32 23 34 44 34
Sorting by the next most significant digit (here the highest digit):
1. Bucket: 11 12
2. Bucket: 23
3. Bucket: 32 32 34 34
4. Bucket: 41 42 44
Recollecting: 11 12 23 32 32 34 34 41 42 44
Pseudo Code
radixsort(A, n)
{
for(i = 0; i < k; i++)
{
for(j = 0; j<si; j++)
bin[j] = EMPTY;](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-62-320.jpg)
![63
for(j = 0; j < n; j++)
move Ai to the end of bin[Ai->fi]
for(j = 0; j < si; j++)
concatenate bin[j] onto the end of A;
}
}
Complexity
Worst case performance O(kN)
Worst case space complexity O(kN) where k is the maximum number of digits.
A variant of the Least Significant Digit radix sort is the Most Significant Digit (MSD) radix sort. It starts
with the most significant digit.
Merge Sort
Merge Sort is a comparison-based sorting algorithm. Most of the used implementation produces a stable
sort.
The algorithm works as follows:
• The unsorted input list is divided in two sub-lists of about half the size of the original
• Each sub-list is sorted recursively by using again a merge sort
• Afterwards the two sub-list are merge into one sorted list
The basic idea behind the Merge Sort is that a smaller list takes less runtime than a bigger and fewer
steps are necessary to construct a sorted list from two sorted lists than from an unsorted list.
Example](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-63-320.jpg)
![64
Figure 18 Merge Sort
Algorithm
#include <stdio.h>
#include <stdlib.h>
#define MAXARRAY 10
void mergesort(int a[], int low, int high);
int main(void)
{
int array[MAXARRAY];
int i = 0;
for(i = 0; i < MAXARRAY; i++)
array[i] = rand() % 100;
printf("Before :");
for(i = 0; i < MAXARRAY; i++)
printf(" %d", array[i]);
printf("n");
mergesort(array, 0, MAXARRAY - 1);
printf("Mergesort :");
for(i = 0; i < MAXARRAY; i++)
printf(" %d", array[i]);
printf("n");
return 0;
}
void mergesort(int a[], int low, int high)](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-64-320.jpg)
![65
{
int i = 0;
int length = high - low + 1;
int pivot = 0;
int merge1 = 0;
int merge2 = 0;
int working[length];
if(low == high)
return;
pivot = (low + high) / 2;
mergesort(a, low, pivot);
mergesort(a, pivot + 1, high);
for(i = 0; i < length; i++)
working[i] = a[low + i];
merge1 = 0;
merge2 = pivot - low + 1;
for(i = 0; i < length; i++)
{
if(merge2 <= high - low)
if(merge1 <= pivot - low)
if(working[merge1] > working[merge2])
a[i + low] = working[merge2++];
else
a[i + low] = working[merge1++];
else
a[i + low] = working[merge2++];
else
a[i + low] = working[merge1++];
}
}
Output
Before : 41 67 34 0 69 24 78 58 62 64
Mergesort : 0 24 34 41 58 62 64 67 69 78
Complexity
Best case performance O(n log n) typical, O(n) natural variant
Worst case performance O(n log n)
Average case performance O(n log n)](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-65-320.jpg)
![66
Bubble Sort
The Bubble Sort is a simple sorting algorithm. It works by repeatedly stepping through a list of data. It
compares each pair of elements and swapping them if they are in wrong order. This is done until no
swap is needed any more.
The name comes from the way smaller elements bubble to the top of the list. It is a comparison sort. The
performance depends strongly on the position of the elements. If the smaller elements are stored at the
end of the list the sort is extremely slowly. If the larger elements are at the beginning this cause no
problem. They are therefore called turtles and rabbits.
Example
First round: 7 2 6 3 9 2 7 6 3 9 2 6 7 3 9 2 6 3 7 9 2 6 3 7 9
Second round: 2 6 3 7 9 2 6 3 7 9 2 3 6 7 9 2 3 6 7 9 2 3 6 7 9
Third round: 2 3 6 7 9 2 3 6 7 9 2 3 6 7 9 2 3 6 7 9 2 3 6 7 9
Algorithm
void bubble(int a[],int n)
{
int i = 0, j = 0, t = 0;
for(i = n-2; i >= 0; i--)
{
for(j = 0; j <= i; j++)
{
if(a[j] > a[j+1])
{
t = a[j];
a[j] = a[j+1];
a[j+1] = t;
}
}
}
}
Variants
Variant of Bubble Sort Description
Od-even sort Parallel version of bubble sort for message passing systems
Cocktail sort Parallel version
Right-to-left Instead of starting from the left side you start from the right side
Table 4 Variants of Bubble Sort](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-66-320.jpg)











![78
Examples for Stacks
Game Tic-Tac-Toe
An implementation of a Stack may require some of the following operations:
• An operation to creating an empty Stack (init)
• An operation to add an element on the top of the Stack (push)
• An operation to remove an element on the top of the Stack (pop)
• An operation to receive the current element on the top of the Stack (top)
• An operation to receive the length of the stack; the number of elements in the Stack (length)
• An operation showing that the maximal capacity of the Stack is reached (full)
In the most program language the implementation of Stack can be done with arrays. The C++ Standard
Template Library provides a Stack Template Class which is restricted to only push/pop operations.
Java's library contains a Stack class that is a specialization of Vector.
Example implementation in C
The Stack is realized by using an array in a structure which additional information about the size of the
Stack.
typedef struct
{
int size;
int items[STACKSIZE];
} STACK;
void push(STACK *ps, int x)
{
if (ps->size++ == STACKSIZE)
{
fputs("Error: stack overflown", stderr);
abort();
}
else
ps->items[ps->size++] = x;
}
int pop(STACK *ps)
{
if (ps->size == 0)
{
fputs("Error: stack underflown", stderr);
abort();
}
else
return ps->items[--ps->size];](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-78-320.jpg)
![79
}
You can also realize the Stack implementation by using pointers.
Queues
A Queue or FIFO (First-In-First-Out) is a Linear List where at one end elements are added and on the
other end elements are removed. The inner elements are not considered. The elements will be
processed in exactly the same order in which they are original placed.
The following operations exists in general for queues
• init() initialize an empty queue.
• isempty() true if the queue is empty
• pop() removes the item at the front of the queue
• push() insert an item at the back of the queue
• size() return the number of elements in the queue
• front() returns a reference to the value at the front of a non-empty queue
The C++ Standard Template Library provides a Queue Template Class.
Example in C
#include <stdio.h>
#define QMAX 100
int Queue[QMAX];
int qLast = 0;
void printqueue()
{
printf ("Queue: ");
for (int i = 0; i < qLast; i++)
printf ("%i ", Queue[i]);
printf ("n");
}
void enqueue(int qItem)](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-79-320.jpg)
![80
{
Queue[qLast] = qItem;
qLast++;
printqueue();
}
int dequeue()
{
int qReturn = Queue[0];
for (int i = 0; i < qLast - 1; i++)
Queue[i] = Queue[i + 1];
qLast--;
printqueue();
return (qReturn);
}
int main()
{
for (int i = 0; i < 10; i++)
enqueue(i);
printf("%dn", dequeue());
return 0;
}
Sorted List
In a Sorted List each element has a key. For this key a complete order relation ≤ exists with:
a ≤ a (reflexivity)
a ≤ b and b ≤ a a = b (anti symmetry)
a ≤ b and b ≤ c a ≤ c (transitivity)
The following operations exist for Sorted List:
• init() initialize an empty Sorted List
• insert() insert an element in the list so that the Sorted List is still sorted
• removefirst() removes the first element in the list (the element with the lowest key)
• getfirst() get the first element from the Sorted List
• search(key) search for an element with given key
• delete(key) delete an element with given key
• length() the size of the Sorted List](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-80-320.jpg)




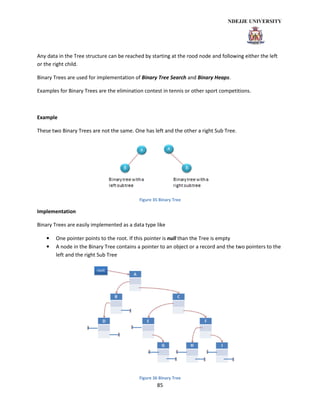






![92
#include <stdlib.h>
struct btreenode
{
struct btreenode *leftchild ;
int data ;
struct btreenode *rightchild ;
};
void insert(struct btreenode **sr, int num);
void inorder(struct btreenode *sr);
void main()
{
struct btreenode *bt = NULL;
int arr[10] = {11, 2, 9, 13, 57, 25, 17, 1, 90, 3};
int i = 0;
printf("Binary tree sort.n");
printf("nArray:n");
for(i = 0; i <= 9; i++)
printf ("%dt", arr[i]);
for (i = 0; i <= 9; i++)
insert (&bt, arr[i]);
printf ("nIn-order traversal of binary tree:n");
inorder(bt);
}
void insert(struct btreenode **sr, int num)
{
if (*sr == NULL)
{
*sr = (btreenode *)malloc(sizeof(struct btreenode));
(*sr)->leftchild = NULL;
(*sr)->data = num;
(*sr)->rightchild = NULL;
}
else
{
if (num < (*sr)->data)
insert(&((*sr)->leftchild), num);
else
insert(&((*sr)->rightchild), num);
}
}
void inorder(struct btreenode *sr)
{
if (sr != NULL)
{
inorder(sr->leftchild);
printf("%dt", sr->data);](https://image.slidesharecdn.com/datastructuresandalgorithm-181023121454/85/Data-structures-and-algorithm-92-320.jpg)

