discrete time signals and systems

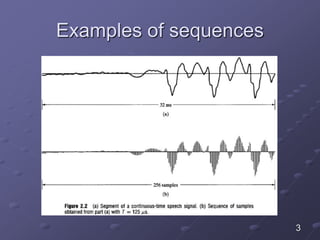
Discrete-Time signals:
sequences
Discreet-Time signals are represented
mathematically as sequences of numbers
The sequence is denoted 𝑥[𝑛], and it is
written formally as
𝑥 = 𝑥 𝑛 ; −∞ < 𝑛 < ∞
where n is an integer number
In practice sequences arises from the
periodic sampling of an analog signal
1

Discrete-Time signals:
sequences
In this case the numeric value of the nth
number in the sequence is equal to the
value of the analog signal, 𝑥 𝑎(𝑡), at time
𝑛𝑇
𝑥 𝑛 = 𝑥 𝑎[𝑛𝑇]
2

Basic sequences and sequence
operation
The product and sum of two sequences x[n]
and 𝑦[𝑛] are defined as the sample by
sample product and sum
Multiplication of a sequence 𝑥[𝑛] by a
number 𝛼 is defined as the multiplication of
each sample value by 𝛼
A sample 𝑦[𝑛] is said to be delayed or shifted
version of 𝑥[𝑛] if 𝑦 𝑛 = 𝑥[ 𝑛 −
4

MATLAB exercise
Record a voice signal using the
audiorecorder function for 5 seconds with
the following specifications
 sampling frequency of 44100
 Number of quantization bits 16
 Number of channels = 1 for mono
 Try to multiply the recorded samples by a
scaling factor of 𝛼 = 0.1 then by 𝛼 = 2 Play
the signal and hear the voice
5

Special sequences Unit sample
sequence
Unit sample sequence is defined as the
sequence
One of the important aspects of the impulse
sequence is that an arbitrary sequence can
be presented as a sum of scaled, delayed
impulses as shown in the next slide
6

Special sequences Unit sample
sequence
In general any sequence can be written as
𝑥 𝑛 = 𝑘=−∞
∞
𝑥 𝑘 𝛿[𝑛 − 𝑘]
7

Special sequences Unit step
sequence
The unit step sequence is given by
8

sequence
The unit step sequence is given by
9

sequence
The unit step sequence in terms of
delayed impulses can be written as 𝑢 𝑛 =
𝛿 𝑛 + 𝛿 𝑛 − 1 + 𝛿 𝑛 − 2 + ⋯ =
𝑘=0
∞
𝛿 𝑛 − 𝑘
Note that the impulse sequence can be
expressed as the first backward difference
of the unit step sequence
𝛿 𝑛 = 𝑢 𝑛 − 𝑢[𝑛 − 1]
10

Special sequences exponential
sequences
Exponential sequence are important in
representing and analyzing linear time
invariant systems
The general form of an exponential sequence
is given by 𝑥 𝑛 = 𝐴𝛼 𝑛
If 𝐴 and 𝛼 are real then the sequence is real
If 0 < 𝛼 < 1 and 𝐴 is positive then the
sequence values are positive and decreasing
with increasing 𝑛
11

Special sequences exponential
sequences
Graphical representation of exponential
sequence
12

Special sequences sinusoidal
sequences
The general form of sinusoidal sequence is
given by 𝑥 𝑛 = 𝐴𝑐𝑜𝑠(𝜔0 𝑛 + ∅) as shown
13

Special sequences sinusoidal and
complex exponential sequence
The exponential sequence 𝑥 𝑛 = 𝐴𝛼 𝑛 with
complex 𝛼 has a real and imaginary parts that
are exponentially weighted sinusoids
If 𝛼 = 𝛼 𝑒 𝑗𝜔0 and 𝐴 = 𝐴 𝑒 𝑗∅ then the sequence
can be expressed in either one of the following
forms
14

Notes about sequences
When discussing either complex exponential signals
of the form 𝑥 𝑛 = 𝐴𝑒 𝑗𝜔0 𝑛 or real sinusoidal signal
of the form 𝑥 𝑛 = 𝐴𝑐𝑜𝑠 𝜔0 𝑛 + ∅ we need only to
consider frequencies in an interval of length of 2𝜋
only because
15

Periodic sequence
A periodic sequence is a sequence that
satisfies the following equation
𝑥 𝑛 = 𝑥[𝑛 + 𝑁],
Where 𝑁 is an integer number
If this condition is tested for the discrete
time sinusoids, then
Which requires
16

Periodic sequence
Where 𝑘 is an integer
A similar statement holds for the complex
exponential
Where 𝑁 is an integer number
Again
17

Example
Determine if the following sequences are
periodic or not. If the sequence is periodic
find its period
a) 𝑥1 𝑛 = cos
𝑛𝜋
4
b) 𝑥2 𝑛 = cos
3𝑛𝜋
4
18

solution
a) For the first sequence we have 𝜔0 𝑁 =
2𝜋k or
𝜋
4
𝑁 = 2𝜋𝑘 → 𝑁 = 8𝑘 since 𝑁 is an
integer value the sequence is periodic
b) For the second sequence 𝜔0 𝑁 = 2𝜋𝑘 or
3𝜋
4
𝑁 = 2𝜋𝑘 → 𝑁 =
8
3
𝑘 since 𝑁 is not an
integer value for 𝑘 = 1 the sequence is
aperiodic if 𝑁 = 8
19

2.2 Discrete time systems
A discrete-time system is a system that
maps an input sequence with an output
sequence 𝑦 𝑛 = 𝑇{𝑥 𝑛 }
20

Discrete time system examples
There are many systems will be
investigated through out this course
Examples of these systems are
1. The ideal delay system which is described
mathematically by 𝑦 𝑛 = 𝑥 𝑛 − 𝑛 𝑑 , −∞ <
𝑛 < ∞
2. Moving average system which is described
mathematically by
1
𝑀1+𝑀2+1 𝑘=−𝑀1
𝑀2
𝑥[𝑛 − 𝑘]
21

Discrete time system
classifications
Systems can be classifieds into one of the
following categories
1. Memoryless Systems. A system is classified
into memoryless system if the output 𝑦 𝑛 at
every value of 𝑛 depends only on the input
of 𝑥[𝑛] at the same value of 𝑛. An example
of a memoryless system is the squarer
system described by 𝑦 𝑛 = 𝑥[𝑛] 2
22

classifications
2. Linear systems. Any system satisfies the
superposition and the scaling property is
classifieds as a linear system. As an
example of a linear system is the
accumulator system described by
𝑦 𝑛 = 𝑘=−∞
𝑛
𝑥[𝑘]
3. Time-invariant system is a system for which
a time shift or delay of the input sequence
causes a corresponding shift in the output
sequence
23

classifications
Example show that the accumulator system
𝑦 𝑛 = 𝑘=−∞
𝑛
𝑥[𝑘] is a time invariant system
solution
Assume that the input to the accumulator is
𝑥1 𝑛 = 𝑥[𝑛 − 𝑛0], then its output is 𝑦1 𝑛 =
𝑘=−∞
𝑛
𝑥1[𝑘] = 𝑘=−∞
𝑛
𝑥[𝑘 − 𝑛0]
Let 𝑘1 = 𝑘 − 𝑛0
This means that
𝑦1 𝑛 = 𝑘=−∞
𝑛−𝑛0
𝑥[𝑘1] = y[n − 𝑛0]
24

classifications
4. Causality, a system is causal if the output
sequence value at the index 𝑛 − 𝑛0 depends
only on the input sequence values for 𝑛 ≤ 𝑛0
For example the forward difference system
described by 𝑦 𝑛 = 𝑥 𝑛 + 1 − 𝑥 𝑛 is not causal
because the current value of the output depends on
future value of the input
Another example is the backward difference system
𝑦 𝑛 = 𝑥 𝑛 − 𝑥[𝑛 − 1] is a causal system since the
output depends only on the present and past
values of the input
25

classifications
5. Stability, a system is stable if and only if
every bounded input sequence produces a
bounded output sequence
Such a system is called BIBO
in equation form
𝑥 𝑛 ≤ 𝐵𝑥 < ∞ → 𝑦 𝑛 ≤ 𝐵𝑦 < ∞
In general any sequence that has the form
𝑦 𝑛 = 𝑘=−∞
𝑛
𝑥[𝑘] < ∞ is stable system
26

Linear time-invariant system
The linear time-invariant system is an
important system since many of the system
we deal with in signal processing are of this
type
The output sequence in response to the
input sequence applied to the input of the
linear time-invariant system is given by the
convolutional sum 𝑦 𝑛 =
𝑘=−∞
∞
𝑥 𝑘 ℎ[𝑛 − 𝑘]
27

In order to compute the convolution we
draw both ℎ 𝑛 − 𝑘 and 𝑥[𝑘] sequences as
shown below
28

From the Figure, we have 𝑦 𝑛 = 0 𝑓𝑜𝑟 𝑛 <
0
The next sequence interval is shown by the
next graph that is 0 ≤ 𝑛 ≤ 𝑁 − 1
29

The output sequence for this interval is
given by
This equation can be solved analytically by
using the geometric series expansion
𝑘=𝑁1
𝑁2
𝑎 𝑘 =
𝑎 𝑁1 − 𝑎 𝑁2 +1
1 − 𝑎
30

The output sequence for this interval is
given by
This equation can be solved analytically by
using the geometric series expansion
𝑘=𝑁1
𝑁2
𝑎 𝑘 =
𝑎 𝑁1 − 𝑎 𝑁2 +1
1 − 𝑎
31

Convolution example
Which yields the following result
𝑦 𝑛 =
𝑘=0
𝑛
𝑎 𝑘
=
1 − 𝑎 𝑛+1
1 − 𝑎
𝑓𝑜𝑟 0 ≤ 𝑛 ≤ 𝑁 − 1
We consider the next interval when 0 < 𝑛 −
𝑁 + 1
The output sequence is given by
32

Convolution example
Which yields the following result
The final answer for the output sequence for
these three intervals is given by
33

Convolution in Matlab
Convolution can be accomplished easily in
matlab by using the function conv(u,v)
The above example can be solved easily in
matalb by using the following code in matlab
n=1:10;
h=ones(1,5);
x=0.4.^n;
Y=conv(x,h);
stem(y);
35

2.4 Properties of linear time
invariant system
The output sequence 𝑦[𝑛] of all LTI are
described by the convolution sum
𝑦 𝑛 =
𝑘=−∞
∞
𝑥 𝑘 ℎ[𝑛 − 𝑘]
Where ℎ[𝑛] is the impulse response of the LTI
system
This means that ℎ[𝑛] is a complete
characterization of the properties of a specific
LTI system
36

Properties of the convolution
sum
commutative
𝑥 𝑛 ∗ 𝑦 𝑛 = 𝑦 𝑛 ∗ 𝑥 𝑛
Distribution over addition
𝑥 𝑛 ∗ ℎ1 𝑛 + ℎ2 𝑛 = 𝑥 𝑛 ∗ ℎ1 𝑛 + 𝑥 𝑛 ∗ ℎ2 𝑛
Associative
𝑦 𝑛 = 𝑥 𝑛 ∗ ℎ1 𝑛 ∗ ℎ2 𝑛 = 𝑥 𝑛 ∗ ℎ1 𝑛 ∗ ℎ2 𝑛
37

Graphical representation of
combined LTI systems
38
Cascaded systems can be presented
by a single system whose impulse
response is given by ℎ 𝑛 = ℎ1[𝑛] ∗
ℎ2[𝑛]. Cascaded systems satisfy the
convolution commutative property
Systems connected in parallel
can be replaced by a single
system whose ℎ 𝑛 = ℎ1 𝑛 +
ℎ2[𝑛].

Stability and causality in terms
of ℎ[𝑛]
LTI are stable if and only if there impulse
response is absolutely summable i.e.
𝑆 =
𝑘=−∞
∞
ℎ[𝑘] < ∞
LTI is causal if ℎ 𝑛 = 0 𝑓𝑜𝑟 𝑛 < 0
Causality means that the difference
equations describing the system can be
solved recursively
39

FIR systems – reflected in the
h[n]
Ideal delay
𝑦 𝑛 = 𝑥 𝑛 − 𝑛 𝑑 , −∞ < 𝑛 < ∞
ℎ 𝑛 = 𝛿 𝑛 − 𝑛 𝑑 , 𝑛 𝑑 𝑝𝑜𝑠𝑖𝑡𝑖𝑣𝑒 𝑖𝑛𝑡𝑒𝑔𝑒𝑟
Forward difference
𝑦 𝑛 = 𝑥 𝑛 + 1 − 𝑥 𝑛
ℎ 𝑛 = 𝛿 𝑛 + 1 − 𝛿 𝑛
Backward difference
𝑦 𝑛 = 𝑥 𝑛 − 𝑥 𝑛 − 1
ℎ 𝑛 = 𝛿 𝑛 − 𝛿[𝑛 − 1]
Finite-duration impulse response (FIR) system are
characterized by an impulse response has that has only a
finite number of nonzero samples
40

IIR systems – reflected in the
ℎ[𝑛]
Accumulator
𝑦 𝑛 =
𝑘=−∞
𝑛
𝑥[𝑘]
ℎ 𝑛 =
𝑘=−∞
𝑛
𝛿[𝑘] = 𝑢[𝑛]
Infinite duration impulse response (IIR) system has ℎ[𝑛]
whose duration extends to infinity
Stability S = 𝑘=−∞
∞
ℎ[𝑘] <?
∞
FIR systems always are stable, if each value of ℎ[𝑛] values is
finite in magnitude
IIR systems can be stable, e.g. ℎ 𝑛 = 𝑎 𝑛 𝑢 𝑛 , 𝑎 < 1 →
𝑛=0
∞
𝑎 𝑛
=
1
1− 𝑎
< ∞
41

Cascading system examples
Determine if the following system is causal or not
Solution
 Since the impulse response of the cascaded
system satisfy ℎ 𝑛 = 0 𝑓𝑜𝑟 𝑛 < 0 the resulting
cascaded system is stable
Any FIR system can be made causal by
cascading it with a sufficiently long delay
42

Cascading system examples
Determine the impulse response of the
following cascaded systems
An inverse system is given by
43

Linear constant-coefficient
difference equations
The Nth order linear constant coefficient
equations are a subclass of linear time
invariant systems
The general form of these equations is
44

Example of difference equations
Write the accumulator system in terms of
Solution
 The accumulator equation is given by
 The output for 𝑛 − 1 can be written as
45

 Now the output sequence can be written as
 Or alternatively it can be written as
 If we compare the last equation with 𝑘=0
𝑁
𝑎 𝑘[𝑛 − 𝑘] =
𝑘=0
𝑀
𝑏 𝑚[𝑚 − 𝑘] we find that 𝑁 = 1, 𝑎0 = 1, 𝑎1 =
− 1, 𝑀 = 0, 𝑏0 = 1
46

The difference equations gives a better
understanding of how we can be
implement the accumulator system in this
example
47

Solving the Linear constant
coefficient difference equations
Difference equations are similar to differential
equations in continuous systems
The solution for the difference equations is
composed from the homogeneous and
particular solutions as described
mathematically by
𝑦 𝑛 = 𝑦𝑝 𝑛 + 𝑦ℎ[𝑛]
48

The homogeneous solution 𝑦ℎ 𝑛 is obtained
with 𝑥 𝑛 = 0
This means that the difference equation reduces
to
𝑘=0
𝑁
𝑎 𝑘 𝑦ℎ[𝑛 − 𝑘] = 0
Since 𝑦ℎ 𝑛 has 𝑁 undetermined coefficients, a
set of 𝑁 auxiliary conditions is required for the
unique specification of 𝑦[𝑛] for a given 𝑥 𝑛
49

These auxiliary conditions might consist of
specifying fixed values of 𝑦[𝑛] at specific values
of 𝑛, such as 𝑦[−1], 𝑦[−2], … , 𝑦[−𝑁]
The above step results in a set of 𝑁 linear
equations for the 𝑁 undetermined coefficients,
which can be solved to produce the required
coefficients
50

Recursive solution of the
The output samples for 𝑛 ≥ 0 can be computed
recursively by rearranging the difference
equation as shown below
𝑦 𝑛 = −
𝑘=1
𝑁
𝑎 𝑘
𝑎0
𝑦 𝑛 − 𝑘 +
𝑘=0
𝑀
𝑏 𝑘
𝑎0
𝑥[𝑛 − 𝑘]
If the input 𝑥[𝑛], together with a set of auxiliary
values 𝑦 −1 , 𝑦 −2 , … , 𝑦[−𝑁] is specified then
the output 𝑦[0] can be computed
51

Recursive solution of the
With 𝑦 0 , 𝑦 −1 , … , 𝑦[−𝑁 + 1] available 𝑦[1] can
be computed
To generate values of 𝑦[𝑛] for 𝑛 < −𝑁, we can
rearrange the linear constant coefficient
difference equation as shown below
𝑦 𝑛 − 𝑁 = −
𝑘=0
𝑁−1
𝑎 𝑘
𝑎 𝑁
𝑦 𝑛 − 𝑘 +
𝑘=0
𝑀
𝑏 𝑘
𝑎 𝑁
𝑥[𝑛 − 𝑘]
52

Recursive computation example
Example: solve the following difference
equation recursively
𝑦 𝑛 = 𝑎𝑦 𝑛 − 1 + 𝑥 𝑛
Assume that the input is 𝑥 𝑛 = 𝐾𝛿 𝑛 and
𝑦 −1 = 𝑐
53

When 𝑛 > −1, we can use recursive
computation as follows
Let 𝑛 = 0 then
𝑦 0 = 𝑎𝑦 0 − 1 + 𝑥 0
𝑦 0 = 𝑎𝑦 −1 + 𝐾𝛿 0
Since 𝑦 −1 = 𝑐, then
𝑦 0 = 𝑎𝑐 + 𝐾
54

Next we do the same procedure when 𝑛 = 1
• 𝑦 1 = 𝑎𝑦 1 − 1 + 𝑥 1
• 𝑦 1 = 𝑎𝑦 0 + 0 = 𝑎 𝑎𝑐 + 𝐾 = 𝑎2
𝑐 + 𝑎𝐾
• 𝑦 2 = 𝑎𝑦 1 + 0 = 𝑎 𝑎2𝑐
+ 𝑎𝐾 = 𝑎3
𝑐 + 𝑎2
𝐾
• 𝑦 3 = 𝑎𝑦 2 + 0 = 𝑎 𝑎3
𝑐 + 𝑎2
𝐾 = 𝑎4
𝑐 + 𝑎3
𝐾
• 𝑦 𝑛 = 𝑎 𝑛+1
𝑐 + 𝑎 𝑛
𝐾
To determine the output for 𝑛 < 0, we express the
difference equations in the form
𝑦 𝑛 − 1 = 𝑎−1
(𝑦 𝑛 − 𝑥 𝑛 )
𝑦 𝑛 = 𝑎−1
(𝑦 𝑛 + 1 − 𝑥 𝑛 + 1 )
55

If we use the auxiliary conditions 𝑦[−1] = 𝑐, we
can compute 𝑦[𝑛] for 𝑛 < −1 as follows
• 𝑦 −2 = 𝑎−1
𝑦 −1 − 𝑥 −1 = 𝑎−1
𝑐
• 𝑦 −3 = 𝑎−1
𝑦 −2 − 𝑥 −2 = 𝑎−1
𝑎−1
𝑐 = 𝑎−2
𝑐
• 𝑦 −4 = 𝑎−1
𝑦 −3 − 𝑥 −3 = 𝑎−1
𝑎−2
𝑐 = 𝑎−3
𝑐
𝑦 𝑛 = 𝑎 𝑛+1
𝑐 𝑓𝑜𝑟 𝑛 ≤ −1
By combining the solutions for 𝑛 > −1 and 𝑛 ≤
− 1, we got the following solution
𝑦 𝑛 = 𝑎 𝑛+1 𝑐
56

2.6 Frequency-domain representation
of discrete time signals and systems
The frequency response of a given system
with impulse response of ℎ[𝑛] is defined
by
𝐻 𝑒 𝑗𝜔
=
𝑘=−∞
∞
ℎ 𝑘 𝑒−𝑗𝜔𝑘
The output of any system characterized by
its frequency response is given by
𝑦 𝑛 = 𝐻 𝑒 𝑗𝜔
𝑒 𝑗𝜔𝑛
57

Frequency response of the ideal
delay system
Example determine the frequency response
of an ideal delay system described by the
following equation
𝑦 𝑛 = 𝑥 𝑛 − 𝑛 𝑑
Solution
To find the frequency response we first find
the impulse response of the system which
can be found by substituting 𝑥 𝑛 = 𝛿 𝑛
58

Frequency response of the ideal
delay system
This means that
𝐻 𝑛 = 𝛿 𝑛 − 𝑛 𝑑
Now the frequency response is given by
𝐻 𝑒 𝑗𝜔
=
𝑛=−∞
∞
𝛿 𝑛 − 𝑛 𝑑 𝑒−𝑗𝜔𝑛
= 𝑒−𝑗𝜔𝑛 𝑑
𝐻 𝑒 𝑗𝜔 can be written in rectangular form as
illustrated below
𝐻 𝑒 𝑗𝜔 = 𝐻 𝑅 𝑒 𝑗𝜔 + 𝐻𝐼 𝑒 𝑗𝜔
𝐻 𝑅 𝑒 𝑗𝜔
= cos(𝜔𝑛 𝑑) , 𝐻𝐼 𝑒 𝑗𝜔
= − sin 𝜔𝑛 𝑑 from
Euler identity
59

2.7 Representation of sequences
by Fourier transforms
In order to represent a given sequence by its
Fourier transform we can use the following
equation
𝑋 𝑒 𝑗𝜔
𝑛=−∞
∞
𝑥 𝑛 𝑒−𝑗𝜔𝑛
However the inverse Fourier transform is given
by
𝑥 𝑛 =
1
2𝜋 −𝜋
𝜋
𝑋 𝑒 𝑗𝜔 𝑒 𝑗𝜔𝑛 𝑑𝜔
60

Representation of sequences by
Fourier transforms
For the discrete time signals, the value of
𝜔 is restricted to an interval of 2𝜋
The low frequency component of discrete
time signals are located around 𝜔 = 0
The high frequency component are
located around 𝜔 = ±𝜋
61

Convergence of the Fourier
transform
In general not all the signals have Fourier
transform
Only the absolutely summable signals
have their Fourier transform exits
Absolutely summable signals are signals
satisfying the following condition
𝑛=−∞
∞
𝑥 𝑛
62

Example
Determine if 𝑥 𝑛 = 𝑎 𝑛 𝑢[𝑛] has a Fourier
transform or not. If the Fourier transform exist,
find the value of 𝑋 𝑒 𝑗𝜔
Solution
The summation
𝑛=−∞
∞
𝑥[𝑛] =
𝑛=0
∞
𝑎 𝑛
=
1
1 − 𝑎
< ∞
If and only if 𝑎 < 1 this means that the discrete
Fourier transform exists only for 𝑎 < 1
63

Example
The summation
𝑋 𝑒 𝑗𝜔
=
𝑛=0
∞
𝑎 𝑛
𝑒−𝑗𝜔𝑛
=
𝑛=0
∞
(𝑎𝑒−𝑗𝜔
) 𝑛
=
1
1 − 𝑎𝑒−𝑗𝜔
If and only if 𝑎 < 1 this means that the discrete
Fourier transform exists only for 𝑎 < 1
64

discrete time signals and systems

More Related Content

What's hot (20)

Viewers also liked (20)

Similar to discrete time signals and systems (20)

Recently uploaded (20)

discrete time signals and systems