Electrochemistry Calculation User Guide Book: Metrohm
- 1. Electrochemistry A workbook for 910 PSTAT mini Monograph
- 3. All rights reserved, including translation rights. Printed in Switzerland by Metrohm Ltd., CH-9101 Herisau, Switzerland. 8.108.5020EN – 2013-01 Barbara Zumbrägel Electrochemistry A workbook for 910 PSTAT mini
- 5. Electrochemistry – A workbook for 910 PSTAT mini 3 Content Content ........................................................................................................................................3 1 Introduction ..........................................................................................................................5 2 Standard reduction potential Reduction potential of different metals........................................................................................9 3 A reversible redox system Cyclic voltammetry with p-aminophenol at slow scan rates .......................................................13 4 A quasi-reversible redox system Cyclic voltammetry with p-aminophenol at fast scan rates.........................................................17 5 An irreversible redox system Cyclic voltammetry with vitamin C.............................................................................................23 6 SAM – Self-assembled monolayers Formation and characterization of self-assembled monolayer....................................................27 7 Quantification of vitamin C Voltammetric determination of vitamin C on a carbon electrode ...............................................35 8 Quantification of mercury Voltammetric determination of mercury at a gold electrode......................................................43 9 Quantification of cadmium and lead Voltammetric determination of cadmium and lead at a mercury film electrode .........................53 10 The principle of a glucose sensor Amperometric detection of glucose at an enzyme modified platinum electrode ........................63 11 Examples Experiment 2: Standard reduction potential...............................................................................75 Experiment 3: A reversible redox system....................................................................................79 Experiment 4: A quasi-reversible redox system...........................................................................81 Experiment 5: An irreversible redox system ................................................................................83 Experiment 6: SAM – Self-assembled monolayers......................................................................85 Experiment 7: Quantification of vitamin C..................................................................................87 Experiment 8: Quantification of mercury....................................................................................95 Experiment 9: Quantification of cadmium and lead ................................................................ 105 Experiment 10: The principle of a glucose sensor.................................................................... 117 12 Abbreviations..................................................................................................................... 127 13 Bibliography ...................................................................................................................... 129
- 7. Introduction Electrochemistry – A workbook for 910 PSTAT mini 5 1 Introduction Electrochemistry has seen a tremendous revival in recent years. As a research tool for physical chemists and having been a sensitive and powerful analytical technique for a long period of time numerous new applications have now brought it back into the technological spotlight. The most important techniques to mention here are related to the production and storage of electrical energy. A few keywords in this context are: solar cells, batteries, fuel cells and electromobility. All of these techniques deal with the production and storage of electrical energy and are based on, or use, electrochemical cells. The development of electrochemical sensors has been an important field for research and development for a number of years. Starting from classical macro electrodes modern developments have brought new types of sensors for the detection of biological molecules or for the detection of low level environmental contaminants. Also, new methods for sensor production have been established: Screen-printing techniques are used to produce sensors for routine measurements as well as for research purposes, lithographic technologies are used to manufacture silicon-based sensors. As well as sensors for single determinations, sensor arrays also exist that permit the determination of a number of substances in parallel. These are known as electronic tongue or electronic nose. Miniaturization of the sensor, as well as the electronics makes it possible to produce systems that allow the measurement of biomolecules or pharmaceutical compounds in vivo. Even structures in nanoscale dimensions can be depicted using technologies like scanning electrochemical microscopy. Another important field of electrochemical application are the techniques used to characterize surface properties: Corrosion measurements characterise the resistance of a metal against the corrosion. Electrochemical plating technologies are used for decorative purposes and more importantly for technical coatings in corrosion protection or in manufacturing printed circuit boards or silicon microprocessors. Last but not least, we should remember the classical quantitative electroanalytical techniques for the determination of trace levels of metals or other electrochemically active substances in environmental samples, in food, in pharmaceuticals, in quality control in the chemical industry, in mining or in the plating industry. A thorough understanding of the basic science is a prerequisite for successful development, manufacture and application of all these technologies. With this monograph Metrohm presents a small collection of basic experiments illustrating some of the essential principles of electrochemistry. The experiments are designed to be carried out with the 910 PSTAT mini potentiostat in combination with the disposable screen-printed electrodes. The experiment description includes detailed information about the material required and a step-by-step guide. Examples are included in the appendix to show what the student can expect. The experiments include the determination of the standard reduction potential of some metal ions using linear sweep voltammetry. Cyclic voltammetry is used for the experiments dealing with the reversibility of electrochemical reactions, the determination of the reaction rate constant and the diffusion coefficient. The fundamentals of quantitative analysis, like linear working range, limit of quantification or the calibration techniques calibration curve and standard addition, are established by means of the determination of vitamin C, mercury, cadmium and lead using differential pulse voltammetry. The change of the surface properties of an electrode after the formation of a self- assembled monolayer of molecules is illustrated and finally the principle of an amperometric glucose sensor is explained.
- 8. Introduction 6 Metrohm Monograph 8.108.5020EN 1.1 General information 1.1.1 The instrument 910 PSTAT mini 1.1.2 The accessories Screen printed electrode USB connector – Connection to the PC (includes power supply) Connector for the electrode cable 6.2163.000 Status LED Green – Instrument connected and ready Orange – Measurement running Red – Current overload Electrode cable 6.2163.000 Measuring vessel cover 6.1412.010 Measuring vessel 6.1412.000 Measuring vessel holder 6.2703.020 Connector for PSTAT mini AE (auxiliary electrode – carbon) RE (reference electrode – silver) Working electrode Carbon 6.1208.110 Gold 6.1208.210 Platinum 6.1208.510 Electrical connections (AE•WE•RE)
- 9. Introduction Electrochemistry – A workbook for 910 PSTAT mini 7 1.1.3 The electrode connection Electrode connection The connector on the electrode cable is marked with SPE (screen printed electrode). This label and the electrical connections on the electrode have to point in the same direction when connecting the electrode. The electrical contacts of the electrode as well as the connector of the electrode cable have to be completely dry and free from contaminants before the electrode is connected. The ingress of moisture into the electrical contact should be avoided in any case. Active electrode surface Touching the active electrode surface with bare fingers should be avoided in any case. The contact of the active electrode surface with the silicon of the measuring vessel cover should be avoided. To fit the electrode into the measuring vessel cover, push the electrical contacts through the silicon rubber. Electrode connector Active electrode surface (WE•AE•RE)
- 11. Standard reduction potential Electrochemistry – A workbook for 910 PSTAT mini 9 2 Standard reduction potential Reduction potential of different metals The reduction potential is a measure for the affinity of a chemical substance to accept electrons. Under given conditions it is specific for the element or substance. In this experiment the reduction behavior of different metal ions will be tested and compared. The determination is carried out by linear sweep voltammetry (LSV). For further reading on LSV see e.g. Metrohm Monograph, Introduction to Polarography and Voltammetry(1) or Monk, Electroanalytical Chemistry(2) . For further reading on the reduction potential see e.g. P.W. Atkins, Physical Chemistry(3) or Hamann and Vielstich, Electrochemistry(4) . 2.1 Accessories and reagents 2.1.1 Accessories 910 PSTAT mini Electrode cable 6.2163.000 Carbon electrode 6.1208.110 (WE – C, AE – C, RE – Ag) Measuring vessel, measuring vessel cover and measuring vessel holder Additional accessories (not included in the scope of delivery of the 910 PSTAT mini) Magnetic stirrer with stirrer bar (e.g. Metrohm 728 Stirrer) Pipettes Volumetric flasks 2.1.2 Reagents Potassium chloride solution, c(KCl) = 3 mol/L, e.g. Metrohm 6.2308.020 Nitric acid, w(HNO3) = 65 %, for trace analysis* , CAS 7697-37-2 Gold standard solution, β(Au) = 1 g/L, H[AuCl4] in 1 mol/L HCl Mercury(II) nitrate monohydrate, Hg(NO3)2 · H2O, puriss. p.a., CAS 7783-34-8 Copper nitrate trihydrate, Cu(NO3)2 · 3 H2O, puriss. p.a., CAS 10031-43-3 Bismuth nitrate pentahydrate, Bi(NO3)3 · 5 H2O, puriss. p.a., CAS 10035-06-0 Lead nitrate, Pb(NO3)2, p.a., CAS 10099-74-8 Ultrapure water type 1 (electrical resistivity > 18.2 MΩ·cm, TOC < 10 ppb) Ready-to-use solutions Supporting electrolyte c(KCl) = 0.1 mol/L c(HNO3) = 0.2 mol/L Pipette 6.67 mL KCl solution (c(KCl) = 3 mol/L) into a 200 mL volumetric flask. Add 2.856 mL nitric acid (w(HNO3) = 65%) and make up to the mark with ultrapure water. * e.g. Merck suprapur® , Sigma-Aldrich TraceSelect® or equivalent
- 12. Standard reduction potential 10 Metrohm Monograph 8.108.5020EN Au stock solution β(Au3+ ) = 1 g/L Can be used as purchased, equals 5.08 mmol/L Au3+ . Bi stock solution c(Bi3+ ) = 0.01 mol/L Weigh in 0.485 g Bi(NO3)3 · 5 H2O and transfer into a 100 mL volumetric flask. Add 2 mL nitric acid (w(HNO3) = 65 %) and shake until everything is dissolved. Carefully add ultrapure water. Make up to the mark with ultrapure water. Cu stock solution c(Cu2+ ) = 0.01 mol/L Weigh in 0.242 g Cu(NO3)2 · 3 H2O and transfer into a 100 mL volumetric flask. Dissolve in approx. 60 mL ultrapure water. Add 2 mL nitric acid (w(HNO3) = 65 %) and make up to the mark with ultrapure water. Hg stock solution c(Hg2+ ) = 0.01 mol/L Weigh in 0.342 g Hg(NO3)2 · H2O and transfer into a 100 mL volumetric flask. Dissolve in approx. 60 mL ultrapure water. Add 2 mL nitric acid (w(HNO3) = 65 %) and make up to the mark with ultrapure water. Pb stock solution c(Pb2+ ) = 0.01 mol/L Weigh in 0.331 g Pb(NO3)2 and transfer into a 100 mL volumetric flask. Dissolve in approx. 60 mL ultrapure water. Add 2 mL nitric acid (w(HNO3) = 65%) and make up to the mark with ultrapure water. 2.2 Reduction of different metals on a carbon electrode Measuring solution 11 mL supporting electrolyte Voltammetric parameters Figure 1: Parameters for testing the reduction potential of different metals (experiment 2.2).
- 13. Standard reduction potential Electrochemistry – A workbook for 910 PSTAT mini 11 2.2.1 Procedure Measurement Enter the voltammetric parameters given in Figure 1. Reduction potential of lead a) Prepare the measuring solution by pipetting 11 mL supporting electrolyte into the measuring vessel. Put a stirrer bar into the measuring vessel. b) Take a new carbon electrode (6.1208.110) and assemble it with the measuring vessel cover. Take care not to touch the active electrode surface with bare fingers. Immerse the electrode into the measuring solution and close the measuring vessel with the measuring vessel cover. c) Switch on the stirrer. d) Make sure that the electrical contacts of the electrode are dry and free from contaminants. Then connect the electrode cable. e) Switch off the stirrer f) Start the measurement. g) Repeat the measurement until the baseline is stable, which usually needs 3 to 5 replications. The solution should be stirred before every measurement, but not during the potential scan. h) Switch on the stirrer and add 0.2 mL of the Pb stock solution (c(Pb2+ ) = 0.01 mol/L). Stir the solution for at least 20 s. i) Switch off the stirrer and record the curve to see the reduction of lead. j) Save curves and parameters with «File / Save as …». Reduction potential of copper Repeat step a) to j) but add 0.2 mL of the Cu stock solution (c(Cu2+ ) = 0.01 mol/L) instead in step h). Reduction potential of bismuth Repeat step a) to j) but add 0.2 mL of the Bi stock solution (c(Bi3+ ) = 0.01 mol/L) instead in step h). Reduction potential of mercury Repeat step a) to j) but add 0.2 mL of the Hg stock solution (c(Hg2+ ) = 0.01 mol/L) instead in step h). Reduction potential of gold Repeat step a) to j) but add 0.4 mL of the Au stock solution (β(Au3+ ) = 1 g/L) instead in step h). Evaluation k) Evaluate the potential at the peak maximum of the reduction signal for the individual metal ions as described in 2.2.2. l) Compare the values for the peak maximum for the different metals and make a list sorted by their reduction potential. m) Compare the observed reduction potentials with data for the standard reduction potential which can be found in literature. Think about reasons for the differences in the values.
- 14. Standard reduction potential 12 Metrohm Monograph 8.108.5020EN 2.2.2 Curve evaluation Compare the baseline of the supporting electrolyte with the curve after the addition of the metal. In scan direction, the first sharp increase in negative current indicates the beginning of the reduction of the added metal. Evaluate the potential of the corresponding peak maximum. Figure 2: Example for the curve evaluation of experiment 2.2. (–– electrolyte, –– with added metal solution) 2.2.3 Additional information Note! Mercury, lead and copper and their salts are very toxic to the environment. If the standard solutions cannot be used anymore take care of an appropriate disposal. It is recommended to use a new electrode for every metal to be tested. In most cases it is not possible to remove the metal quantitatively from the working electrode. Any remaining metals can influence the reduction behavior of other metals in the following experiments. Begin of reduction Scan direction Peak maximum
- 15. A reversible redox system Electrochemistry – A workbook for 910 PSTAT mini 13 3 A reversible redox system Cyclic voltammetry with p-aminophenol at slow scan rates Cyclic voltammetry is a valuable tool to study the mechanism and the reversibility of electrode reactions. The organic compound p-aminophenol is used as an example for a substance showing reversible behavior at slow scan rates. In this experiment the reversibility will be reviewed and the diffusion coefficient of the oxidized and reduced species will be calculated from the experimental data using the Randles-Sevcik equation. For further reading on cyclic voltammetry and reversibility of redox systems see e.g. Bond, Broadening Electrochemical Horizons(5) or Bard and Faulkner, Electrochemical Methods(6) . 3.1 Accessories and reagents 3.1.1 Accessories 910 PSTAT mini Electrode cable 6.2163.000 Electrode 6.1208.110 (WE – C, AE – C, RE – Ag) Measuring vessel, measuring vessel cover and measuring vessel holder Additional accessories (not included in the scope of delivery of the 910 PSTAT mini) Magnetic stirrer with stirrer bar (e.g. Metrohm 728 Stirrer) Pipettes Volumetric flasks 3.1.2 Reagents Ammonia solution, for analysis, w(NH3) = 25 %, CAS 1336-21-6 Hydrochloric acid, for analysis, w(HCl) = 30 %, CAS 7647-01-0 Sulfuric acid, for analysis, w(H2SO4) = 96 %, CAS 7664-93-9 p-Aminophenol hydrochloride, H2NC6H4OH · HCl, MW 145.59 g/mol, CAS 51-78-5 Ultrapure water type 1 (electrical resistivity > 18.2 MΩ·cm, TOC < 10 ppb) Ready-to-use solutions Ammonia buffer pH 9.5 c(NH4Cl) = 1 mol/L c(NH3) = 2 mol/L Fill approx. 300 mL ultrapure water into a 500 mL volumetric flask. Carefully add 53 mL HCl (30 %) and 112.5 mL NH3 (25 %). After cooling down to room temperature make up to the mark with ultrapure water. Diluted sulfuric acid c(H2SO4) = 0.5 mol/L Fill approx. 900 mL ultrapure water into a 1 L volumetric flask. Carefully add 27.78 mL sulfuric acid (w(H2SO4) = 96%). Attention, the solution becomes very hot! After cooling down to room temperature make up to the mark with ultrapure water.
- 16. A reversible redox system 14 Metrohm Monograph 8.108.5020EN p-AP stock solution c(p-AP) = 0.01 mol/L Dissolve 0.145 g p-aminophenol hydrochloride in 10 mL c(H2SO4) = 0.5 mol/L. Fill up to 100 mL with ultrapure water 3.2 Experiment 3.2.1 Procedure Measuring solution 10 mL H2O 1 mL ammonia buffer pH 9.5 0.1 mL p-AP stock solution (c(p-AP) = 0.01 mol/L) Voltammetric parameters Figure 3: Parameters for experiment 3.2. Measurement a) Prepare the measuring solution by pipetting 10 mL ultrapure water, 1 mL ammonia buffer and 0.10 mL p-AP stock solution (0.01 mol/L) into the measuring vessel. Put a stirrer bar into the measuring vessel and stir the solution well. b) Take a new carbon electrode (6.1208.110) and assemble it with the measuring vessel cover. Take care not to touch the active electrode surface with bare fingers. Immerse the electrode into the measuring solution and close the measuring vessel with the measuring vessel cover. c) Make sure that the electrical contacts of the electrode are dry and free from contaminants. Then connect the electrode cable. d) Record the cyclic voltammogram with the voltammetric parameters from Figure 3. Make sure the stirrer is switched off during the measurement. Save the voltammogram together with the method parameters.
- 17. A reversible redox system Electrochemistry – A workbook for 910 PSTAT mini 15 e) Stir the solution. f) Change the scan rate in the voltammetric parameters to 0.02 V/s and record another cyclic voltammogram using the same electrode. Make sure the stirrer is switched off during the measurement. g) Save the voltammogram together with the method parameters. h) Repeat step e) to g) also with scan rates of 0.03, 0.04 and 0.05 V/s. Evaluation i) Evaluate peak height and peak potential for the different scan rates as described in 3.2.2. j) Use the criteria mentioned in 3.2.3 to assess if the reaction is reversible. Propose a mechanism for the reaction that is observed in the cyclic voltammogram. k) Plot a graph with the peak height as a function of the square root of the scan rate √ for the anodic signal as well as the cathodic signal. Calculate the linear regression for the two curves and the diffusion coefficient for the reduced and the oxidized species using the slope of the linear regression and the Randles-Sevcik equation. 3.2.2 Curve evaluation Evaluate the peak potential and the peak height of the anodic peak as well as of the cathodic peak. For the peak potential the cursor or «Peak measurement tool 1» can be used. For the evaluation of the peak height it is recommended to use the «Step measurement tool» since this allows the evaluation from the residual current to the peak maximum. Figure 4: Example for the evaluation of peak height in experiment 3.2.
- 18. A reversible redox system 16 Metrohm Monograph 8.108.5020EN 3.2.3 Additional information Criteria for a reversible process The peak potential is independent of the scan rate . The difference between anodic peak potential and cathodic peak potential is described by (Eq. 1). (Eq. 1) – Peak potential of the anodic signal – Peak potential of the cathodic signal – Molar gas constant (8.314 J·mol-1 ·K-1 ) – Temperature in K – Faraday constant (9.648·104 C·mol-1 ) – Number of electrons For T = 298 K (Eq. 2) Peak height √ . Anodic peak height and cathodic peak height are equal. Randles-Sevcik equation √ (Eq. 3) – Peak height – Area of the working electrode – Concentration – Diffusion coefficient – scan rate Stability of p-aminophenol p-Aminophenol is not very stable in alkaline solution. Therefore the measurements at different scan rates should be done without interruption. In alkaline solution p-aminophenol is oxidized by oxygen from ambient air to 4-imino-cyclohexa-2,5- dienone, which can then easily polymerize: Figure 5: Oxidation of p-aminophenol The reaction is indicated by a slight yellow color of the measuring solution. The polymer forms a brown precipitate. NH2 OH O2 NH O O H2 OH 1/2 + +
- 19. A quasi-reversible redox system Electrochemistry – A workbook for 910 PSTAT mini 17 4 A quasi-reversible redox system Cyclic voltammetry with p-aminophenol at fast scan rates Cyclic voltammetry is a valuable tool to study the mechanism and the reversibility of electrode reactions. Richard S. Nicholson(7) developed and published a simple method to evaluate the standard rate constant for the electron transfer from the peak potential separation and the scan rate of a quasi-reversible system. As an example for a quasi-reversible system p-aminophenol will be used again, but unlike in experiment 3 the measurement will be carried out at faster scan rates. In this experiment the reversibility will be reviewed and Nicholson’s method will be used to calculate the standard rate constant from the experimental data. For further reading on cyclic voltammetry and reversibility of redox systems see e.g. Bond, Broadening Electrochemical Horizons(5) or Bard and Faulkner, Electrochemical Methods(6) . 4.1 Accessories and reagents 4.1.1 Accessories 910 PSTAT mini Electrode cable 6.2163.000 Electrode 6.1208.110 (WE – C, AE – C, RE – Ag) Measuring vessel, measuring vessel cover and measuring vessel holder Additional accessories (not included in the scope of delivery of the 910 PSTAT mini) Magnetic stirrer with stirrer bar (e.g. Metrohm 728 Stirrer) Pipettes Volumetric flasks 4.1.2 Reagents Ammonia solution, for analysis, w(NH3) = 25 %, CAS 1336-21-6 Hydrochloric acid, for analysis, w(HCl) = 30 %, CAS 7647-01-0 Sulfuric acid, for analysis, w(H2SO4) = 96 %, CAS 7664-93-9 p-Aminophenol hydrochloride, H2NC6H4OH · HCl, MW 145.59 g/mol, CAS 51-78-5 Ultrapure water type 1 (electrical resistivity > 18.2 MΩ·cm, TOC < 10 ppb) Ready-to-use solutions Ammonia buffer pH 9.5 c(NH4Cl) = 1 mol/L c(NH3) = 2 mol/L Fill approx. 300 mL ultrapure water into a 500 mL volumetric flask. Carefully add 53 mL HCl (30 %) and 112.5 mL NH3 (25 %). After cooling down to room temperature make up to the mark with ultrapure water. Diluted sulfuric acid c(H2SO4) = 0.5 mol/L Fill approx. 900 mL ultrapure water into a 1 L volumetric flask. Carefully add 27.78 mL sulfuric acid (w(H2SO4) = 96 %). Attention, solution becomes very hot! After cooling down to room temperature make up to the mark with ultrapure water.
- 20. A quasi-reversible redox system 18 Metrohm Monograph 8.108.5020EN p-AP stock solution c(p-AP) = 0.01 mol/L Dissolve 0.145 g p-aminophenol hydrochloride in 10 mL c(H2SO4) = 0.5 mol/L. Fill up to 100 mL with ultrapure water. 4.2 Experiment 4.2.1 Procedure Measuring solution 10 mL H2O 1 mL ammonia buffer pH 9.5 0.1 mL p-AP stock solution (0.01 mol/L) Voltammetric parameters Figure 6: Parameters for experiment 4.2. Measurement a) Prepare the measuring solution by pipetting 10 mL ultrapure water, 1 mL ammonia buffer and 0.10 mL p-AP stock solution (0.01 mol/L) into the measuring vessel. Put a stirrer bar into the measuring vessel and stir the solution well. b) Take a new carbon electrode (6.1208.110) and assemble it with the measuring vessel cover. Take care not to touch the active electrode surface with bare fingers. Immerse the electrode into the measuring solution and close the measuring vessel with the measuring vessel cover. c) Make sure that the electrical contacts of the electrode are dry and free from contaminants. Then connect the electrode cable. d) Record the cyclic voltammogram with the voltammetric parameters shown in Figure 6. Make sure the stirrer is switched off during the measurement.
- 21. A quasi-reversible redox system Electrochemistry – A workbook for 910 PSTAT mini 19 e) Save the voltammogram together with the method parameters. f) Stir the solution. g) Change the scan rate in the voltammetric parameters to 0.2 V/s and record another cyclic voltammogram using the same electrode. Make sure the stirrer is switched off during the measurement. h) Save the voltammogram together with the method parameters. i) Repeat step f) to h) also with scan rates of 0.3, 0.4 and 0.5 V/s. Evaluation j) Evaluate peak height and peak potential for the different scan rates as described in 4.2.2. k) Use the criteria mentioned in 4.2.3 to assess if the reaction is reversible. l) Calculate the standard rate constant from the peak potential separation in your experiment. The necessary formula (Eq. 4) and the tabled values for the charge transfer parameter 𝜓 (Figure 8) can be found in 4.2.3. 4.2.2 Curve evaluation Evaluate the peak potential and the peak height of the anodic signal as well as of the cathodic signal. For the peak potential the cursor or «Peak measurement tool 1» can be used. For the evaluation of the peak height it is recommended to use the «Step measurement tool» since this allows the evaluation from the residual current to the peak maximum. Figure 7: Example for the evaluation of peak height in experiment 4.2.
- 22. A quasi-reversible redox system 20 Metrohm Monograph 8.108.5020EN 4.2.3 Additional information Standard rate constant for electron transfer according to Nicholson(7) 𝜓 √ (Eq. 4) √ 𝜓 – Charge transfer parameter – Charge transfer coefficient – Standard rate constant for electron transfer – Scan rate – Diffusion coefficient of the reduced species – Diffusion coefficient of the oxidized species – Number of electrons – Faraday constant (9.648·104 C·mol-1 ) – Molar gas constant (8.314 J·mol-1 ·K-1 ) – Temperature in K (a) * † / mV 20 61 7 63 6 64 5 65 4 66 3 68 2 72 1 84 0.75 92 0.5 105 0.35 121 0.25 141 0.1 212 (b) Figure 8: Variation of peak potential separations with kinetic parameters for cyclic voltammetry. (a) table (b) semi-logarithmic plot of the table values (7) For 𝜓 the values of are nearly independent from if 0.3 < < 0.7, therefore can be used as a good approximation for the calculation. If experiment 3 is not carried out to determine the diffusion coefficients, the following values can be used for the calculation: = 3.81·10-5 cm2 ·s-1 = 3.17·10-5 cm2 ·s-1 * See (Eq. 4) † For = 0.5 50 70 90 110 130 150 170 190 210 230 0.1 1 10 D E p ·n / mV
- 23. A quasi-reversible redox system Electrochemistry – A workbook for 910 PSTAT mini 21 Criteria for a reversible process The peak potential is independent of the scan rate . The difference between anodic peak potential and cathodic peak potential is described by (Eq. 2). (for T = 298 K) (Eq. 2) Peak height √ . Anodic peak height and cathodic peak height are equal. Stability of p-aminophenol p-Aminophenol is not very stable in alkaline solution. Therefore the measurements at different scan rates should be done without interruption. In alkaline solution p-aminophenol is oxidized by oxygen from ambient air to 4-imino-cyclohexa-2,5- dienone, which can then easily polymerize: Figure 9: Oxidation of p-aminophenol The reaction is indicated by a slight yellow color of the measuring solution. The polymer forms a brown precipitate. Auto current ranging For fast scan rates the auto current ranging has to be switched off. The current range of the potentiostat has to be set to ±100 µA or ±10 µA depending on the maximum current that needs to be measured. NH2 OH O2 NH O O H2 OH 1/2 + +
- 25. An irreversible redox system Electrochemistry – A workbook for 910 PSTAT mini 23 5 An irreversible redox system Cyclic voltammetry with vitamin C Cyclic voltammetry is a valuable tool to study the mechanism and the reversibility of electrode reactions. Ascorbic acid, also known as vitamin C, is used as an example for a substance showing irreversible behavior. In this experiment the reversibility will be reviewed. For further reading on cyclic voltammetry and reversibility of redox systems see e.g. Bond, Broadening Electrochemical Horizons(5) or Bard and Faulkner, Electrochemical Methods(6) . 5.1 Accessories and reagents 5.1.1 Accessories 910 PSTAT mini Electrode cable 6.2163.000 Electrode 6.1208.110 (WE – C, AE – C, RE – Ag) Measuring vessel, measuring vessel cover and measuring vessel holder Additional accessories (not included in the scope of delivery of the 910 PSTAT mini) Magnetic stirrer with stirrer bar (e.g. Metrohm 728 Stirrer) Pipettes Volumetric flasks 5.1.2 Reagents Potassium chloride solution, c(KCl) = 3 mol/L, e.g. Metrohm 6.2308.020 Ascorbic acid, puriss. p.a., C6H8O6, CAS 50-81-7 Ultrapure water type 1 (electrical resistivity > 18.2 MΩ·cm, TOC < 10 ppb) Ready-to-use solutions Supporting electrolyte c(KCl) = 0.1 mol/L Pipette 6.67 mL KCl solution (c(KCl) = 3 mol/L) into a 200 mL volumetric flask and make up to the mark with ultrapure water. Vitamin C standard solution c(Vitamin C) = 0.1 mol/L Weigh in 0.88 g ascorbic acid and transfer it into a 50 mL volumetric flask. Dissolve and make up to the mark with ultrapure water. Since vitamin C is sensitive against oxygen and light it is recommended to use deaerated ultrapure water for the preparation and keep the standard in the dark. Only use standard solution that is prepared the same day.
- 26. An irreversible redox system 24 Metrohm Monograph 8.108.5020EN 5.2 Experiment 5.2.1 Procedure Measuring solution 11 mL supporting electrolyte 0.1 mL Vitamin C standard solution (0.1 mol/L) Voltammetric parameters Figure 10: Parameters for experiment 5.2. Measurement a) Prepare the measuring solution by pipetting 11 mL supporting electrolyte and 0.10 mL vitamin C standard solution (0.1 mol/L) into the measuring vessel. Put a stirrer bar into the measuring vessel and stir the solution well. b) Take a new carbon electrode (6.1208.110) and assemble it with the measuring vessel cover. Take care not to touch the active electrode surface with bare fingers. Immerse the electrode into the measuring solution and close the measuring vessel with the measuring vessel cover. c) Make sure that the electrical contacts of the electrode are dry and free from contaminants. Then connect the electrode cable. d) Record the cyclic voltammogram with the voltammetric parameters from Figure 10. Make sure the stirrer is switched off during the measurement. Save the voltammogram together with the method parameters. e) Stir the solution. f) Change the scan rate in the voltammetric parameters to 0.1 V/s and record another cyclic voltammogram using the same electrode. Make sure the stirrer is switched off during the measurement. g) Save the voltammogram together with the method parameters. h) Repeat step e) to g) also with scan rates of 0.15, 0.2 and 0.25 V/s.
- 27. An irreversible redox system Electrochemistry – A workbook for 910 PSTAT mini 25 Evaluation i) Evaluate peak height and peak potential for the different scan rates as described in 5.2.2. j) Assess the influence of the scan rate on peak height and peak potential, find arguments why it is an irreversible reaction and suggest a mechanism for the reaction that is seen in the voltammogram. 5.2.2 Curve evaluation Evaluate the peak potential and the peak height of the anodic peak. For the peak potential the cursor or «Peak measurement tool 1» can be used. For the evaluation of the signal height it is recommended to use the «Step measurement tool» since this allows the evaluation from the residual current to the peak maximum. Figure 11: Example for the evaluation of peak height in experiment 5.2.
- 29. SAM – Self-assembled monolayers Electrochemistry – A workbook for 910 PSTAT mini 27 6 SAM – Self-assembled monolayers Formation and characterization of self-assembled monolayer «Molecular self-assembly is the assembly of molecules without guidance or management from an outside source.»(8) An increasing number of publications can be found on this topic. The field of applications ranges from biology and biosensors to electrochemistry and electronics to material science and nanotechnology. A simple way of generating a self-assembled and organized monolayer is to use the affinity of a thiol compound to a gold substrate. This experiment is a brief introduction into coating and shows a simple electrochemical method to assess the quality of the self-assembled monolayer. For further reading on self-assembly and the theory of self-assembled monolayers see e.g. Sigma-Aldrich, Molecular Self-Assembly(8) or Bond, Broadening Electrochemical Horizons(5) . Figure 12: Illustration of the assembly of 2-mercapto acetic acid (2-MAA), 3-mercapto propionic acid (3-MPA), 6-mercapto hexanoic acid (6-MHA) and 11-mercapto undecanoic acid (11-MUA) to a gold electrode surface. 6.1 Accessories and reagents 6.1.1 Accessories 910 PSTAT mini Electrode cable 6.2163.000 Electrode 6.1208.210 (WE – Au, AE – C, RE – Ag) Measuring vessel, measuring vessel cover and measuring vessel holder Additional accessories (not included in the scope of delivery of the 910 PSTAT mini) Magnetic stirrer with stirrer bar (e.g. Metrohm 728 Stirrer) Pipettes
- 30. SAM – Self-assembled monolayers 28 Metrohm Monograph 8.108.5020EN Volumetric flasks Ultrasonic bath Small sample containers with cap (inner diameter approx. 1.5 cm) to hold the electrode during self-assembly (e.g. Metrohm sample tubes 15 mL (6.2747.000)) Tweezers 6.1.2 Reagents 2-Mercapto acetic acid, HSCH2COOH, CAS 68-11-1 3-Mercapto propionic acid, HSC2H4COOH, CAS 107-96-0 6-Mercapto hexanoic acid, HSC5H10COOH, CAS 17689-17-7 11-Mercapto undecanoic acid, HSC10H20COOH, CAS 71310-21-9 Ethanol, puriss. p.a., CAS 64-17-5 Potassium hexacyanoferrate(III), K3[Fe(CN)6], puriss. p.a., CAS 13746-66-2 Acetic acid, w(CH3COOH) = 100 %, for trace analysis* , CAS 64-19-7 Ammonia solution, w(NH3) = 25 %, for trace analysis* , CAS 1336-21-6 Ultrapure water type 1 (electrical resistivity > 18.2 MΩ·cm, TOC < 10 ppb) Ready-to-use solutions Ammonium acetate buffer pH 4.6 c(CH3COOH) = 2 mol/L c(NH3) = 1 mol/L Fill approx. 300 mL ultrapure water into a 500 mL volumetric flask. Carefully add 55.5 mL acetic acid (100 %) and 37 mL NH3 (25 %). Make up to the mark with ultrapure water. 2-MAA stock solution c(MAA) = 0.1 mol/L Dissolve 92 mg 2-mercapto acetic acid (equals 69.4 µL) in 10 mL ethanol. The solution is stable for at least a month if stored in the freezer. 3-MPA stock solution c(MPA) = 0.1 mol/L Dissolve 106 mg 3-mercapto propionic acid (equals 87 µL) in 10 mL ethanol. The solution is stable for at least a month if stored in the freezer. 6-MHA stock solution c(MHA) = 0.1 mol/L Dissolve 148 mg 6-mercapto hexanoic acid (equals 138.4 µL) in 10 mL ethanol. The solution is stable for at least a month if stored in the freezer. 11-MUA stock solution c(MUA) = 0.1 mol/L Dissolve 218 mg 11-mercapto undecanoic acid in 10 mL ethanol. The solution is stable for at least a month if stored in the freezer. Hexacyanoferrate(III) stock solution c([Fe(CN)6]3- ) = 0.1 mol/L Dissolve 0.33 g potassium hexacyanoferrate(III) in 10 mL ultrapure water. The solution should be prepared freshly at the day of use. * e.g. Merck suprapur® , Sigma-Aldrich TraceSelect® or equivalent
- 31. SAM – Self-assembled monolayers Electrochemistry – A workbook for 910 PSTAT mini 29 6.2 Experiment 6.2.1 Self-assembly The self-assembly happens spontaneously, however the electrode needs to be prepared for the coating. The electrode has to be cleaned initially by sonication in ethanol. Then it is electrochemically conditioned before it is immersed into the coating solution for the self-assembly of the monolayer. The coating usually takes about two days. First results can be seen after 24 h. But results are usually much better if 48 h are allowed for self-assembly. Cleaning of the electrode Cleaning solution Ethanol Cleaning procedure a) Place all gold electrodes (6.1208.210) that should be coated side by side in a bowl with ethanol (cleaning solution) and sonicate them for approx. 15 minutes. The electrodes should not be placed on top of each other to prevent damage of the active electrode surface. Electrochemical conditioning of the electrode Conditioning solution 10 mL H2O 1 mL ammonium acetate buffer pH 4.6 Voltammetric parameters Figure 13: Parameters for the cyclic voltammetric conditioning of the electrode in experiment 6.2.
- 32. SAM – Self-assembled monolayers 30 Metrohm Monograph 8.108.5020EN Conditioning procedure b) Prepare the conditioning solution by pipetting 10 mL ultrapure water and 1 mL ammonium acetate buffer pH 4.6 into the measuring vessel. Put a stirrer bar into the measuring vessel and stir the solution well. c) Enter the parameters given in Figure 13. d) Take one of the cleaned gold electrodes out of the ethanol. Rinse it thoroughly with ultrapure water and assemble it with the measuring vessel cover. Take care not to touch the active electrode surface with bare fingers. Immerse the electrode into the conditioning solution and close the measuring vessel with the measuring vessel cover. e) Use a soft tissue to thoroughly dry the electrical contacts of the electrode. Make sure that the contacts are completely dry and free from contaminants before connecting the electrode cable. f) For electrochemical conditioning run one cyclic voltammogram in the conditioning solution. Self-assembly Coating solutions* 2-MAA 2.97 mL ethanol 0.03 mL 2-MAA stock solution 3-MPA 2.97 mL ethanol 0.03 mL 3-MPA stock solution 6-MHA 2.97 mL ethanol 0.03 mL 6-MHA stock solution 11-MUA 2.97 mL ethanol 0.03 mL 11-MUA stock solution Coating procedure g) Prepare the 2-MAA coating solution by pipetting 2.97 mL ethanol and 0.03 mL 2-MAA stock solution into a sample tube 6.2747.000. If another vessel with different dimensions is used, the volumes have to be adapted. It is important that the active electrode surface can be completely immersed into the coating solution. h) Take a gold electrode after electrochemical conditioning (step f) and thoroughly rinse it with ultrapure water. Take care not to touch the active electrode surface with bare fingers. i) Immerse the electrode into the sample tube with the 2-MAA coating solution. One sample tube can hold two electrodes back-to-back for modification. Close the sample tube with the cap to prevent the evaporation of ethanol. j) Repeat step g) to i) with other cleaned electrodes and immerse them into sample tubes filled with an appropriate volume of 3-MPA coating solution, 6-MHA coating solution or 11-MUA coating solution. Make sure the sample tubes are properly closed to prevent the loss of ethanol. k) Leave the electrodes in the coating solutions for 2 days. First results can be seen after 24 h. But results are usually much better if 48 h are allowed for self-assembly. * Volumes are for the use of Metrohm sample tubes 15 mL (6.2747.000)
- 33. SAM – Self-assembled monolayers Electrochemistry – A workbook for 910 PSTAT mini 31 6.2.2 Characterization of the monolayer by cyclic voltammetry The thickness of a monolayer ranges from a few tenth of a nanometer to a few nanometers, a size which cannot be seen visually. Therefore technical equipment is required to characterize the monolayer. Usually sophisticated instruments, like scanning tunneling microscopes (STM) or atomic force microscopes (AFM), are used. For studying the structure of monolayers these techniques are essential, but sometimes a more simple approach will do. In a cyclic voltammetric measurement the reaction [Fe(CN)6]3- + e- ⇌ [Fe(CN)6]4- shows one distinct oxidation and one distinct reduction signal. The presence of a coating at the electrode will have an influence on the measurement of these signals. This effect can be used for an indirect characterization and comparison of electrodes with different coatings. Measuring solution 10 mL H2O 1 mL ammonium acetate buffer 0.1 mL hexacyanoferrate(III) stock solution Voltammetric parameters Figure 14: Parameters for testing the monolayer by cyclic voltammetry (experiment 6.2). Measurement a) Prepare the measuring solution by pipetting 10 mL ultrapure water, 1 mL ammonium acetate buffer pH 4.6 and 0.1 mL hexacyanoferrate(III) stock solution into the measuring vessel. Put a stirrer bar into the measuring vessel and stir the solution well. b) Use tweezers to take the electrode out of the 2-MAA coating solution. c) Rinse the electrode thoroughly with ultrapure water and assemble it with the measuring vessel cover. Take care not to touch the active electrode surface with bare fingers. Immerse the electrode into the measuring solution and close the measuring vessel with the measuring vessel cover.
- 34. SAM – Self-assembled monolayers 32 Metrohm Monograph 8.108.5020EN d) Use a soft tissue to thoroughly dry the electrical contacts of the electrode. Make sure that the contacts are completely dry and free from contaminants before connecting the electrode cable. e) Record the cyclic voltammogram with the voltammetric parameters given Figure 14. Make sure the stirrer is switched off during the measurement. f) Repeat step b) to e) with electrodes coated with 3-MPA, 6-MHA and 11-MUA instead of 2- MAA. Evaluation g) Evaluate peak height of the cathodic signal as described in 6.2.3. h) Plot a graph of the peak height as a function of the number of C atoms in the spacer group in the molecule. What can be observed? 6.2.3 Curve evaluation In principle the reduction and the oxidation signal can be used for the characterization. But in the described measuring solution the effect of the monolayer on this cathodic signal is usually more pronounced. This signal is related to the reduction [Fe(CN)6]3- + e- ⟶ [Fe(CN)6]4- . For the evaluation of the peak height it is recommended to use the «Step measurement tool». Figure 15: Example for the evaluation of peak height in experiment 6.2.
- 35. SAM – Self-assembled monolayers Electrochemistry – A workbook for 910 PSTAT mini 33 6.2.4 Additional information Note! 2-mercapto acetic acid and 3-mercapto propionic acid are toxic to the environment. If their solutions cannot be used anymore take care of an appropriate disposal. The process of self-assembly is rather sensitive to contamination of the reagents and electrodes. Therefore it is recommended to: Work in a clean environment. Wear gloves when handling the electrodes, since the oil from finger prints can inhibit the adsorption of the thiols. Make sure that all equipment (glassware, sample tubes, tweezers, …) is sufficiently clean. If you are not sure, everything should be rinsed several times with ethanol. New accessories which were not used for this experiment before, especially the sample tubes, should be soaked in ethanol for a few days. Label the volumetric flasks and sample tubes and always use the same containers for the experiment. Further useful information on the theory of self-assembly and on the preparation of SAM can be found in literature e.g. from Sigma-Aldrich (8) .
- 37. Quantification of vitamin C Electrochemistry – A workbook for 910 PSTAT mini 35 7 Quantification of vitamin C Voltammetric determination of vitamin C on a carbon electrode As discussed in experiment 5, vitamin C can be easily oxidized to dehydroascorbic acid on a carbon electrode: Figure 16: Oxidation of vitamin C Besides kinetic studies this reaction can also be used to determine the concentration of vitamin C in samples. Vitamin C has antioxidant properties and can be found in many foodstuffs. It is often determined by titration, however voltammetry is more selective since other oxidizing or reducing substances do not interfere. The determination is carried out by differential pulse voltammetry (DP). DP shows increased sensitivity compared to linear sweep voltammetry (LSV) and cyclic voltammetry (CV). Therefore DP is the method of choice for quantitative determinations. For further reading on differential pulse votlammetry and on the quantification of vitamin C see e.g. Thomas and Henze, Voltammetric Analysis(9) . In the first part of the experiment the limits of this method, like linear working range and limit of quantification, will be determined. With this background the concentration of vitamin C in a multivitamin product will be determined in the second part of the experiment. The quantification will be carried out by calibration curve technique as well as by standard addition technique. 7.1.1 Accessories 910 PSTAT mini Electrode cable 6.2163.000 Electrode 6.1208.110 (WE – C, AE – C, RE – Ag) Measuring vessel, measuring vessel cover and measuring vessel holder Additional accessories (not included in the scope of delivery of the 910 PSTAT mini) Magnetic stirrer with stirrer bar (e.g. Metrohm 728 Stirrer) Pipettes Volumetric flasks 7.1.2 Reagents Ascorbic acid, puriss. p.a., C6H8O6, CAS 50-81-7 Acetic acid, w(CH3COOH) = 100 %, for trace analysis* , CAS 64-19-7 Ammonia solution, w(NH3) = 25 %, for trace analysis* , CAS 1336-21-6 Ultrapure water type 1 (electrical resistivity > 18.2 MΩ·cm, TOC < 10 ppb) * e.g. Merck suprapur® , Sigma-Aldrich TraceSelect® or equivalent O OH O H O O H O H H + e O O O H O H O O - 2 - 2
- 38. Quantification of vitamin C 36 Metrohm Monograph 8.108.5020EN Ready-to-use solutions Ammonium acetate buffer pH 4.6 c(CH3COOH) = 2 mol/L c(NH3) = 1 mol/L Fill approx. 300 mL ultrapure water into a 500 mL volumetric flask. Carefully add 55.5 mL acetic acid (100 %) and 37 mL NH3 (25 %). Make up to the mark with ultrapure water. Vitamin C standard stock solution β(Vitamin C) = 10 g/L Weigh in 0.5 g ascorbic acid and transfer it into a 50 mL volumetric flask. Dissolve and make up to the mark with ultrapure water. Since vitamin C is sensitive to oxygen and light it is recommended to use deaerated ultrapure water for the preparation and keep the standard in the dark. Only use standard solution that is prepared the same day. Vitamin C standard solution β(Vitamin C) = 1 g/L Use deaerated ultrapure water to dilute 1 mL vitamin C standard stock solution to 10 mL. 7.2 Experiment 7.2.1 Linear working range Measuring solution 10 mL H2O 1 mL ammonium acetate buffer pH 4.6 0.02 mL vitamin C standard stock solution (β(Vitamin C) = 10 g/L) Voltammetric parameters Figure 17: Parameters for the determination of vitamin C (experiment 7.2).
- 39. Quantification of vitamin C Electrochemistry – A workbook for 910 PSTAT mini 37 Measurement a) Prepare the measuring solution by pipetting 10 mL H2O, 1 mL ammonium acetate buffer and 0.02 mL vitamin C standard stock solution (β(Vitamin C) = 10 g/L) into the measuring vessel. Put a stirrer bar into the measuring vessel and stir the solution well. b) Take a new carbon electrode (6.1208.110) and assemble it with the measuring vessel cover. Take care not to touch the active electrode surface with bare fingers. Immerse the electrode into the measuring solution and close the measuring vessel with the measuring vessel cover. c) Make sure that the electrical contacts of the electrode are dry and free from contaminants. Then connect the electrode cable. d) Record the voltammogram with the voltammetric parameters shown in Figure 17. Make sure the stirrer is switched off during the measurement. e) Save the voltammogram together with the method parameters. f) Add another 0.02 mL of the vitamin C standard stock solution (β(Vitamin C) = 10 g/L). Stir the solution. g) Record another voltammogram using the same electrode. Make sure the stirrer is switched off during the measurement. h) Save the voltammogram together with the method parameters. i) Repeat step f) to h) until you have recorded curves with 10 different concentrations. Evaluation j) Evaluate the peak height for the individual concentrations as described in 7.2.4. k) Plot a graph with the peak height as a function of the concentration. l) From the graph determine the concentration range where there is a linear relation between the concentration and the peak height. 7.2.2 Limit of quantification In the literature many different approaches for the determination of the limit of determination (LOD) and the limit of quantification (LOQ) are described. The choice is from the simple consideration of the background noise as a measure for the sensitivity to rather complex statistical examinations of the error of the measurement, which requires numerous measuring. For practical application the so called «regression approach»(10) was found to be very useful. On the one hand it is easy to carry out, on the other hand it provides realistic values for the critical value or critical level (LC) and minimum quantifiable (true) value or quantification limit (LQ), as the LOD and the LOQ should be named according to IUPAC(11) . In principle the regression approach is a simplified statistical approach. It uses the residual standard deviation of a calibration curve recorded in the concentration range of the LOQ for the calculation. The calibration curve has to fulfill the following requirements: Linear relation between concentration and signal, calibration curve y = A + B·x Blank measurement (c = 0) has to be included in the calibration curve 5 to 10 calibration standards, calibration points equidistant 5 to 10 replications per standard, same number of replications per standard Min. 40 measuring points for c ≠ 0 Lowest concentration in the range of LOQ Highest concentration 10 ... 30 · LOD Standard addition can be used to record the calibration curve Standard deviation is homogenous (homoscedastic) For the calculations the following rules should be considered:
- 40. Quantification of vitamin C 38 Metrohm Monograph 8.108.5020EN Blank signals (c = 0) are included in the calculation of the residual standard deviation . Blank signals (c = 0) are not included for the calculation of parameters A (intercept) and B (slope) of the linear regression. Formulas y = A + B x (Eq. 5) y – Peak height x – Concentration of the analyte A – Intercept of the linear regression B – Slope of the linear regression ∑ ( ̂ ) (Eq. 6) – Standard error of estimate (residual standard deviation) in regression – Variance of – Signal value of the ith point in the regression ̂ – Regression value of the signal at the ith point of the linear regression – Number of points on the regression – Number of calibration standards – Number of regression parameters (for linear regression = 2) oncentration (Eq. 7) oncentration 10 (Eq. 8) Recording the calibration curve for the determination of LOQ Measuring solution 10 mL H2O 1 mL ammonium acetate buffer pH 4.6 Standard addition 5 additions of 0.02 mL standard (β(Vitamin C) = 1 g/L) each. Voltammetric parameters See Figure 17. Measurement a) Prepare the measuring solution by pipetting 10 mL H2O and 1 mL ammonium acetate buffer into the measuring vessel. Put a stirrer bar into the measuring vessel and stir the solution well. b) Take a new carbon electrode (6.1208.110) and assemble it with the measuring vessel cover. Take care not to touch the active electrode surface with bare fingers. Immerse the electrode into the measuring solution and close the measuring vessel with the measuring vessel cover. c) Make sure that the electrical contacts of the electrode are dry and free from contaminants. Then connect the electrode cable. d) Record the voltammogram with the voltammetric parameters shown in Figure 17. Make sure the stirrer is switched off during the measurement.
- 41. Quantification of vitamin C Electrochemistry – A workbook for 910 PSTAT mini 39 e) Stir the solution and repeat the measurement of the blank (c = 0). Make sure the stirrer is switched off during the measurement. In total 10 replications are required. f) Save the voltammograms together with the method parameters. g) Add 0.02 mL of the vitamin C standard solution (β(Vitamin C) = 1 g/L). Stir the solution. h) Record another voltammogram using the same electrode. Make sure the stirrer is switched off during the measurement. i) Stir the solution and repeat the measurement of this concentration. Make sure the stirrer is switched off during the measurement. In total 10 replications are required. j) Save the voltammograms together with the method parameters. k) Repeat point g) to j) until you have recorded curves with 5 different concentrations. Evaluation l) Evaluate the peak height for the individual concentrations as described in 7.2.4. m) Plot a graph with the peak height as a function of concentration. n) Calculate the linear regression of the calibration curve. o) Calculate the residual standard deviation of the calibration curve. p) Using the residual standard deviation calculate the LOD and the LOQ of the vitamin C determination. 7.2.3 Determination of vitamin C in multivitamin products The voltammetric determination of vitamin C in a sample requires the calibration of the method. In principle there are two ways, calibration curve or standard addition. Carry out both and discuss advantages and disadvantages of the two calibration techniques. Decide, which one is recommended for this application. Calibration curve Measuring solution «calibration curve» 10 mL H2O 1 mL ammonium acetate buffer pH 4.6 0.05 mL vitamin C standard solution (β(Vitamin C) = 1 g/L) Measuring solution «sample» 10 mL H2O 1 mL ammonium acetate buffer pH 4.6 0.5 mL sample solution Voltammetric parameters See Figure 17. Recording the calibration curve a) Prepare the measuring solution «calibration curve» by pipetting 10 mL H2O, 1 mL ammonium acetate buffer and 0.05 mL vitamin C standard solution (β(Vitamin C) = 1 g/L) into the measuring vessel. Put a stirrer bar into the measuring vessel and stir the solution well. b) Take a new carbon electrode (6.1208.110) and assemble it with the measuring vessel cover. Take care not to touch the active electrode surface with bare fingers. Immerse the electrode into the measuring solution and close the measuring vessel with the measuring vessel cover.
- 42. Quantification of vitamin C 40 Metrohm Monograph 8.108.5020EN c) Make sure that the electrical contacts of the electrode are dry and free from contaminants. Then connect the electrode cable. d) Record the voltammogram with the voltammetric parameters from Figure 17. Make sure the stirrer is switched off during the measurement. Save the voltammogram together with the method parameters. e) Add 0.05 mL of the vitamin C standard solution (β(Vitamin C) = 1 g/L). Stir the solution. f) Record another voltammogram using the same electrode. Make sure the stirrer is switched off during the measurement. g) Save the voltammogram together with the method parameters. h) Repeat step e) to g) until you have recorded curves with 8 to 10 different concentrations. Establishing the calibration curve i) Evaluate the peak height for the individual concentrations as described in 7.2.4. j) Plot a graph with peak height as a function of the concentration and calculate the linear regression of the calibration curve. Determination in the sample k) Prepare the measuring solution «sample» by pipetting 10 mL H2O, 1 mL ammonium acetate buffer and 0.5 mL sample solution into the measuring vessel. Put a stirrer bar into the measuring vessel and stir the solution well. l) Take a new carbon electrode (6.1208.110) and assemble it with the measuring vessel cover. Take care not to touch the active electrode surface with bare fingers. Immerse the electrode into the measuring solution and close the measuring vessel with the measuring vessel cover. m) Make sure that the electrical contacts of the electrode are dry and free from contaminants. Then connect the electrode cable. n) Record the voltammogram with the voltammetric parameters from Figure 17. Make sure the stirrer is switched off during the measurement. Save the voltammogram together with the method parameters. o) Evaluate the peak height for the vitamin C in the sample as described in 7.2.4. p) Compare the peak height with the calibration curve and calculate the concentration of vitamin C in the sample. Standard addition Measuring solution sample 10 mL H2O 1 mL ammonium acetate buffer pH 4.6 0.5 mL sample solution Standard addition Concentration is quantified by 2 additions of 0.1 mL standard (β(Vitamin C) = 1 g/L). Voltammetric parameters See Figure 17.
- 43. Quantification of vitamin C Electrochemistry – A workbook for 910 PSTAT mini 41 Measurement a) Prepare the measuring solution by pipetting 10 mL H2O, 1 mL ammonium acetate buffer and 0.5 mL sample (e.g. multi-vitamin drink) into the measuring vessel. Put a stirrer bar into the measuring vessel and stir the solution well. b) Take a new carbon electrode (6.1208.110) and assemble it with the measuring vessel cover. Take care not to touch the active electrode surface with bare fingers. Immerse the electrode into the measuring solution and close the measuring vessel with the measuring vessel cover. c) Make sure that the electrical contacts of the electrode are dry and free from contaminants. Then connect the electrode cable. d) Record the voltammogram with the voltammetric parameters from Figure 17. Make sure the stirrer is switched off during the measurement. Save the voltammogram together with the method parameters. e) Add 0.1 mL of the vitamin C standard solution (β(Vitamin C) = 1 g/L). Stir the solution. f) Record another voltammogram using the same electrode. Make sure the stirrer is switched off during the measurement. g) Save the voltammogram together with the method parameters. h) Add another 0.1 mL of the vitamin C standard solution (β(Vitamin C) = 1 g/L). Stir the solution. i) Record another voltammogram using the same electrode. Make sure the stirrer is switched off during the measurement. j) Save the voltammogram together with the method parameters. Evaluation k) Evaluate the peak height for the sample and the two standard additions as described in 7.2.4. l) Plot a graph with peak height as a function of the concentration. The concentration in the sample is set to zero. m) Calculate the linear regression for the standard addition curve. n) Extrapolate the linear regression onto the x-axis (concentration axis) to get the negative concentration of vitamin C in the measuring solution. Calculate the concentration of vitamin C in the sample from this value.
- 44. Quantification of vitamin C 42 Metrohm Monograph 8.108.5020EN 7.2.4 Curve evaluation For the evaluation of the peak height «Peak measurement tool 1» can be used. Peak potential of vitamin C is approx. +0.2 V. Figure 18: Example for the evaluation of peak height (c(vitamin C) 55 mg/L) in experiment 7.2. 7.2.5 Additional information The lifetime of the carbon electrode is limited. If measurements are done in clean standard solutions, several measurements at thesame electrode are possible. A calibration curve for example can be recorded using just one electrode. However, as soon as the matrix of a real sample is involved, the lifetime decreases. For samples usually only one determination including the standard additions is possible. A further determination at thesame electrode is not possible anymore.
- 45. Quantification of mercury Electrochemistry – A workbook for 910 PSTAT mini 43 8 Quantification of mercury Voltammetric determination of mercury at a gold electrode Mercury and its compounds are toxic and therefore their quantification, especially in environmental samples, is of great interest. The determination of mercury by anodic stripping voltammetry (ASV) is relatively easy. Stripping voltammetry in general is a two-step method which consists of a preconcentration and a subsequent determination step. The preconcentration allows a significant increase in sensitivity compared to a direct measurement. For the determination of mercury the preconcentration step is a reduction. Mercury ions in the measuring solution are reduced at the gold working electrode and deposited at the gold as an amalgam. Preconcentration: Hg2+ + 2 e- Hg0 (Au) In the subsequent determination step the mercury is anodically stripped off the electrode, which means the deposited mercury is re-oxidized. Anodic stripping: Hg0 (Au) Hg2+ + 2 e- The determination is carried out by differential pulse voltammetry (DP). DP shows increased sensitivity compared to linear sweep voltammetry (LSV) and cyclic voltammetry (CV). Therefore DP is the method of choice for quantitative determinations. For further reading on differential pulse voltammetry and on the quantification of mercury see e.g. Thomas and Henze, Voltammetric Analysis(9) or Metrohm Application Bulletin 96/5, Determination of mercury(12) . In the first part of the experiment the limits of this method, like linear working range and limit of quantification, will be determined. With this background information the concentration of mercury in ambient air will be determined in the second part. This quantification will be carried out by calibration curve technique as well as standard addition technique. 8.1 Accessories and reagents 8.1.1 Accessories 910 PSTAT mini Electrode cable 6.2163.000 Electrode 6.1208.210 (WE – Au, AE – C, RE – Ag) Measuring vessel and measuring vessel cover Additional accessories (not included in the scope of delivery of the 910 PSTAT mini) Magnetic stirrer with stirrer bar (e.g. Metrohm 728 Stirrer) Pipettes Volumetric flasks Equipment for sampling mercury in air Air pump with adjustable gas flow Sorbent tubes Anasorb C300 (500 mg) as specified in ISO 17733(13) Water bath
- 46. Quantification of mercury 44 Metrohm Monograph 8.108.5020EN 8.1.2 Reagents Perchloric acid, for trace analysis* , w(HClO4) = 70% Sulfuric acid, for trace analysis* , w(H2SO4) = 96%, CAS 7664-93-9 Ethylenediaminetetraacetic acid disodium salt dihydrate, for analysis, Na2C10H14N2O8 · 2 H2O, Na2EDTA, CAS 6381-92-6 Sodium chloride, for trace analysis* , NaCl, CAS 7647-14-5 Nitric acid, for trace analysis* , w(HNO3) = 65% Hg standard stock solution, β(Hg2+ ) = 1 g/L (available commercially) Ultrapure water type 1 (electrical resistivity > 18.2 MΩ·cm, TOC < 10 ppb) Ready-to-use solutions Supporting electrolyte c(H2SO4) = 2 mol/L c(Na2EDTA) = 0.02 mol/L c(NaCl) = 0.05 mol/L Weigh in 0.372 g Na2EDTA and 0.146 g NaCl and transfer both into a 50 mL volumetric flask. Dissolve it in approx. 40 mL ultrapure water. Carefully add 5.56 mL concentrated H2SO4. Attention solution becomes hot! After cooling down to room temperature make up to the mark with ultrapure water. 10 mg/L Hg standard solution β(Hg) = 10 mg/L Fill approx. 40 mL ultrapure water into a 50 mL volumetric flask. Add 50 µL concentrated HNO3 (65%) and 500 µL Hg standard stock solution (1 g/L). Make up to the mark with ultrapure water. * e.g. Merck suprapur® , Sigma-Aldrich TraceSelect® or equivalent
- 47. Quantification of mercury Electrochemistry – A workbook for 910 PSTAT mini 45 8.2 Experiment 8.2.1 Initial preparation of the electrode Conditioning solution 11 mL H2O 0.1 mL HClO4 Conditioning parameters Figure 19: Parameters for the conditioning of the gold electrode for the determination of mercury (experiment 8.2). Conditioning a) Prepare the conditioning solution by pipetting 11 mL H2O and 0.1 mL HClO4 into the measuring vessel. Put a stirrer bar into the measuring vessel and stir the solution well. b) Take a new gold electrode (6.1208.210) and assemble it with the measuring vessel cover. Take care not to touch the active electrode surface with bare fingers. Immerse the electrode into the conditioning solution and close the measuring vessel with the measuring vessel cover. c) Make sure that the electrical contacts of the electrode are dry and free from contaminants. Then connect the electrode cable. d) Run the conditioning with the conditioning parameters given in Figure 19. The stirrer has to be switched on during «tcond» and «tdep» but switched off during «tequil» and the potential scan. Usually the electrode is well conditioned after 20 replications. 8.2.2 Linear working range Measuring solution 10 mL H2O 1 mL supporting electrolyte 0.04 mL Hg standard solution (β(Hg) = 10 mg/L)
- 48. Quantification of mercury 46 Metrohm Monograph 8.108.5020EN Voltammetric parameters Figure 20: Parameters for the determination of mercury on a gold electrode (experiment 8.2). Measurement a) Condition a new electrode as described in 8.2.1 Initial preparation of the electrode. b) Rinse the electrode well with ultrapure water. Take care not to touch the active electrode surface with bare fingers. c) Prepare the measuring solution by pipetting 10 mL H2O, 1 mL supporting electrolyte and 0.04 mL Hg standard solution (β(Hg) = 10 mg/L) into the measuring vessel. Put a stirrer bar into the measuring vessel and stir the solution well. d) With the measuring vessel cover assembled immerse the electrode into the measuring solution and close the measuring vessel. e) Make sure that the electrical contacts of the electrode are dry and free from contaminants. Then connect the electrode cable. f) Record the voltammogram with the parameters given in Figure 20. The stirrer has to be switched on during «tcond» and «tdep» but switched off during «tequil» and the whole potential scan. g) Save the voltammogram together with the method parameters. h) Add another 0.04 mL Hg standard solution (β(Hg) = 10 mg/L). Stir the solution well. i) Record another voltammogram using the same electrode and parameters. The stirrer has to be switched on during «tcond» and «tdep» but switched off during «tequil» and the whole potential scan. j) Save the voltammogram together with the method parameters. k) Repeat step h) to j) until you recorded curves for 6 to 8 different concentrations. Evaluation l) Evaluate the peak height of the mercury signal for the individual concentrations as described in 8.2.5. m) Plot a graph with peak height as a function of the concentration.
- 49. Quantification of mercury Electrochemistry – A workbook for 910 PSTAT mini 47 n) From the graph determine the concentration range where there is a linear relation between concentration and peak height. 8.2.3 Limit of quantification In the literature many different approaches for the determination of the limit of determination (LOD) and the limit of quantification (LOQ) are described. The choice is from the simple consideration of the background noise as a measure for the sensitivity to rather complex statistical examinations of the error of the measurement, which requires numerous measuring. For practical application the so called «regression approach»(10) was found to be very useful. On the one hand it is easy to carry out, on the other hand it provides realistic values for the critical value or critical level (LC) and minimum quantifiable (true) value or quantification limit (LQ), as the LOD and the LOQ should be named according to IUPAC(11) . In principle the regression approach is a simplified statistical approach. It uses the residual standard deviation of a calibration curve recorded in the concentration range of the LOQ for the calculation. The calibration curve has to fulfill the following requirements: Linear relation between concentration and signal, calibration curve y = A + B x Blank measurement (c = 0) has to be included in the calibration curve 5 to 10 calibration standards, calibration points equidistant 5 to 10 replications per standard, same number of replications per standard Min. 40 measuring points for c ≠ 0 Lowest concentration in the range of LOQ Highest concentration 10 ... 30 * LOD Standard addition can be used to record the calibration curve Standard deviation is homogenous (homoscedastic) For the calculations the following rules should be considered: Blank signals (c = 0) are included in the calculation of the residual standard deviation . Blank signals (c = 0) are not included for the calculation of parameters A (intercept) and B (slope) of the linear regression. Formulas y = A + B x (Eq. 5) y – Peak height x – Concentration of the analyte A – Intercept of the linear regression B – Slope of the linear regression ∑ ( ̂ ) (Eq. 6) – Standard error of estimate (residual standard deviation) in regression – Variance of – Signal value of the ith point in the regression ̂ – Regression value of the signal at the ith point of the linear regression – Number of points on the regression – Number of calibration standards – Number of regression parameters (for linear regression = 2)
- 50. Quantification of mercury 48 Metrohm Monograph 8.108.5020EN oncentration (Eq. 7) oncentration 10 (Eq. 8) Recording the calibration curve for the determination of LOQ Measuring solution 10 mL H2O 1 mL supporting electrolyte Standard addition 5 additions of 0.020 mL Hg standard solution (β(Hg) = 10 mg/L) each. Voltammetric parameters See Figure 20. Measurement a) Condition a new electrode as described in 8.2.1 Initial preparation of the electrode. b) Rinse the electrode well with ultrapure water. Take care not to touch the active electrode surface with bare fingers. c) Prepare the measuring solution by pipetting 10 mL H2O and 1 mL supporting electrolyte into the measuring vessel. Put a stirrer bar into the measuring vessel and stir the solution well. d) With the measuring vessel cover assembled immerse the electrode into the measuring solution and close the measuring vessel. e) Make sure that the electrical contacts of the electrode are dry and free from contaminants. Then connect the electrode cable. f) Record the voltammogram with the parameters given in Figure 20. The stirrer has to be switched on during «tcond» and «tdep» but switched off during «tequil» and the whole potential scan. g) Stir the solution and repeat the measurement of the blank (c = 0). In total 8 replications are required. h) Save the voltammograms together with the method parameters. i) Add 0.02 mL of the Hg standard solution (β(Hg) = 10 mg/L). Stir the solution well. j) Record again 8 voltammograms with this concentration. The stirrer has to be switched on during «tcond» and «tdep» but switched off during «tequil» and the whole potential scan. k) Save the voltammograms together with the method parameters. l) Repeat step i) to k) until you have recorded curves with 5 different concentrations. Evaluation m) Evaluate the peak height for the individual concentrations as described in 8.2.5. n) Plot a graph with the peak height as a function of the concentration. o) Calculate the linear regression of the calibration curve. p) Calculate the residual standard deviation of the calibration curve. q) Using the residual standard deviation calculate the LOD and the LOQ for the determination of mercury.
- 51. Quantification of mercury Electrochemistry – A workbook for 910 PSTAT mini 49 8.2.4 Determination of mercury in air The working range of the mercury determination with the described parameters is approximately in the middle and upper ppb range. An interesting application in this concentration range is the determination of mercury in workplace air. In many countries the permissible exposure limit is 0.1 mg/m3 as specified by e.g. TRGS 900(14) , Germany or OSHA(15) , USA. The determination of mercury in air consists of two parts, the sampling and the voltammetric determination. The sampling is carried out by the so-called pumped sampling. Air is drawn through a sorbent tube by means of an air pump. Mercury in the air adsorbs to the sorbent and from this sorbent a test solution is prepared in which the mercury concentration can be determined. A detailed description for the sampling of mercury in air can be found in ISO 17733(13) . Figure 21: Schematic setup for the sampling of mercury in air. The voltammetric determination of the mercury concentration in the test solution requires the calibration of the method. In principle there are two ways, calibration curve or standard addition. Carry out both and discuss advantages and disadvantages of the two calibration techniques. Decide which one is recommended for this application. Calibration curve Measuring solution «calibration curve» 10 mL H2O 1 mL supporting electrolyte 0.04 mL Hg Standard solution (β(Hg) = 10 mg/L) Measuring solution «sample» 10 mL H2O 1 mL supporting electrolyte 0.5 mL test solution Voltammetric parameters See Figure 20. Recording the calibration curve a) Condition a new electrode as described in 8.2.1 Initial preparation of the electrode. b) Rinse the electrode well with ultrapure water. Take care not to touch the active electrode surface with bare fingers. c) Prepare the measuring solution «calibration curve» by pipetting 10 mL H2O, 1 mL supporting electrolyte and 0.04 mL Hg standard solution (β(Hg) = 10 mg/L) into the measuring vessel. Put a stirrer bar into the measuring vessel and stir the solution well. d) With the measuring vessel cover assembled immerse the electrode into the measuring solution and close the measuring vessel. e) Make sure that the electrical contacts of the electrode are dry and free from contaminants. Then connect the electrode cable. flow meter sorbent tube air pump connecting tube air flow glass wool sorbent
- 52. Quantification of mercury 50 Metrohm Monograph 8.108.5020EN f) Record the voltammogram with the parameters given in Figure 20. The stirrer has to be switched on during «tcond» and «tdep» but switched off during «tequil» and the whole potential scan. Save the voltammogram together with the method parameters. g) Add 0.02 mL of the Hg standard solution (β(Hg) = 10 mg/L). Stir the solution. h) Record another voltammogram using the same electrode and parameters. The stirrer has to be switched on during «tcond» and «tdep» but switched off during «tequil» and the whole potential scan. i) Save the voltammogram together with the method parameters. j) Repeat step g) to i) until you have recorded curves with 8 to 10 different concentrations. Establishing the calibration curve k) Evaluate the peak height for the individual concentrations as described in 8.2.5. l) Plot a graph with peak height as a function of the concentration and calculate the linear regression of the calibration curve. Determination in the sample m) Condition a new electrode as described in 8.2.1 Initial preparation of the electrode. n) Rinse the electrode well with ultrapure water. Take care not to touch the active electrode surface with bare fingers. o) Prepare the measuring solution «calibration curve» by pipetting 10 mL H2O, 1 mL supporting electrolyte and 0.5 mL test solution into the measuring vessel. Put a stirrer bar into the measuring vessel and stir the solution well. p) With the measuring vessel cover assembled immerse the electrode into the measuring solution and close the measuring vessel. q) Make sure that the electrical contacts of the electrode are dry and free from contaminants. Then connect the electrode cable. r) Record the voltammogram with the same parameters used to record the calibration curve. The stirrer has to be switched on during «tcond» and «tdep» but switched off during «tequil» and the whole potential scan. Save the voltammogram together with the method parameters. Concentration evaluation s) Evaluate the peak height for mercury in the test solution as described in 8.2.5. t) Compare the peak height with the calibration curve and calculate the concentration of mercury in the test solution. u) From the concentration in the test solution calculate the concentration of mercury with respect to the air volume sampled.
- 53. Quantification of mercury Electrochemistry – A workbook for 910 PSTAT mini 51 Standard addition Measuring solution 10 mL H2O 1 mL supporting electrolyte 0.5 mL test solution Standard addition Concentration is quantified by 2 additions of 0.025 mL Hg standard solution (β(Hg) = 10 mg/L). Voltammetric parameters See Figure 20. Determination in the sample a) Condition a new electrode as described in 8.2.1 Initial preparation of the electrode. b) Rinse the electrode well with ultrapure water. Take care not to touch the active electrode surface with bare fingers. c) Prepare the measuring solution by pipetting 10 mL H2O, 1 mL supporting electrolyte and 0.5 mL test solution into the measuring vessel. Put a stirrer bar into the measuring vessel and stir the solution well. d) With the measuring vessel cover assembled immerse the electrode into the measuring solution and close the measuring vessel. e) Make sure that the electrical contacts of the electrode are dry and free from contaminants. Then connect the electrode cable. f) Record the voltammogram with the parameters given in Figure 20. The stirrer has to be switched on during «tcond» and «tdep» but switched off during «tequil» and the whole potential scan. Save the voltammogram together with the method parameters. g) Add 0.025 mL Hg standard solution (β(Hg) = 10 mg/L). Stir the solution. h) Record another voltammogram using the same electrode and parameters. The stirrer has to be switched on during «tcond» and «tdep» but switched off during «tequil» and the whole potential scan. i) Save the voltammogram together with the method parameters. j) Add another 0.025 mL Hg standard solution (β(Hg) = 10 mg/L). Stir the solution. k) Record another voltammogram using the same electrode and parameters. The stirrer has to be switched on during «tcond» and «tdep» but switched off during «tequil» and the whole potential scan. l) Save the voltammogram together with the method parameters. Concentration evaluation m) Evaluate the peak height for mercury for the sample and the two standard additions as described in 8.2.5. n) Plot a graph with the peak height as a function of the concentration. The concentration in the sample is set to zero. o) Calculate the linear regression for the standard addition curve. p) Extrapolate the linear regression onto the x-axis (concentration axis) to get the negative concentration of mercury in the measuring solution. Calculate the concentration of mercury in the test solution. q) From the concentration in the test solution calculate the concentration of mercury with respect to the air volume sampled.
- 54. Quantification of mercury 52 Metrohm Monograph 8.108.5020EN 8.2.5 Curve evaluation For the evaluation of the peak height «peak measurement tool 1» can be used. Peak potential of mercury is approx. +0.45 V Figure 22: Example for the evaluation of peak height (c(Hg) 90 µg/L) in experiment 8.2. 8.2.6 Additional information Note! Mercury is very toxic to the environment. If the standard solution cannot be used anymore take care of an appropriate disposal. The lifetime of the gold electrode is limited. If measurements are done in clean standard solutions several measurements on the same electrode are possible. A calibration curve for example can be recorded using just one electrode. But as soon as the matrix of a real sample is involved, the electrode’s lifetime decreases. For samples approx. 5 determinations including the standard additions are possible.
- 55. Quantification of cadmium and lead Electrochemistry – A workbook for 910 PSTAT mini 53 9 Quantification of cadmium and lead Voltammetric determination of cadmium and lead at a mercury film electrode Cadmium and lead, as many other heavy metals, are toxic and therefore their quantification is of great interest. At a mercury film electrode (MFE) both metals can easily be determined side by side. A mercury film electrode is usually a carbon electrode with a thin film of metallic mercury plated to form the actually working electrode material. The determination of cadmium and lead is carried out by anodic stripping voltammetry (ASV). Stripping voltammetry in general is a two-step method which consists of a preconcentration and a subsequent determination step. The preconcentration allows a significant increase in sensitivity compared to a direct measurement. For the determination of cadmium and lead the preconcentration step is a reduction. Cadmium and lead ions in the measuring solution are reduced at the mercury film electrode and dissolved in the mercury as an amalgam. Preconcentration: Cd2+ + 2 e- Cd0 (Hg) Pb2+ + 2 e- Pb0 (Hg) In the subsequent determination step the cadmium and the lead are anodically stripped off the electrode, which means the deposited metals are re-oxidized. Anodic stripping: Cd0 (Hg) Cd2+ + 2 e- Pb0 (Hg) Pb2+ + 2 e- The determination is carried out by differential pulse voltammetry (DP). DP shows increased sensitivity compared to linear sweep voltammetry (LSV) and cyclic voltammetry (CV). Therefore DP is the method of choice for quantitative determinations. For further reading on differential pulse voltammetry and on the quantification of cadmium and lead on the MFE see e.g. Thomas and Henze, Voltammetric Analysis(9) or Metrohm Application Bulletin 254/1, Determination of zinc, cadmium, lead and copper(16) . In the first part of the experiment the deposition potential (potential applied for preconcentration) is optimized. In the second part the limits of this method, like linear working range and limit of quantification, are determined. With this background information the concentration of cadmium and lead in articles of daily use are determined in the third part. The quantification is carried out by standard addition technique. 9.1 Accessories and reagents 9.1.1 Accessories 910 PSTAT mini Electrode cable 6.2163.000 Electrode 6.1208.110 (WE – C, AE – C, RE – Ag) Measuring vessel and measuring vessel cover Additional accessories (not included in the scope of delivery of the 910 PSTAT mini) Magnetic stirrer with stirrer bar (e.g. Metrohm 728 Stirrer) Pipettes Volumetric flasks
- 56. Quantification of cadmium and lead 54 Metrohm Monograph 8.108.5020EN 9.1.2 Reagents Acetic acid, w(CH3COOH) = 100 %, for trace analysis* , CAS 64-19-7 Ammonia solution, w(NH3) = 25 %, for trace analysis* , CAS 1336-21-6 Hydrochloric acid, w(HCl) = 30 %, for trace analysis* , CAS 7647-01-0 Hg standard stock solution, β(Hg2+ ) = 1 g/L (available commercially) Cd standard stock solution, β(Cd2+ ) = 1 g/L (available commercially) Pb standard stock solution, β(Pb2+ ) = 1 g/L (available commercially) Nitric acid, for trace analysis* , w(HNO3) = 65% Ultrapure water type 1 (electrical resistivity > 18.2 MΩ·cm, TOC < 10 ppb) Ready-to-use solutions Hg plating solution β(Hg) = 20 mg/L c(HCl) = 0.1 mol/L Fill approx. 30 mL ultrapure water into a 50 mL volumetric flask. Add 1 mL Hg standard stock solution (β(Hg2+ ) = 1 g/L) and 0.5 mL HCl (30 %). Make up to the mark with ultrapure water. Buffer pH 4.4 c(CH3COOH) = 2 mol/L c(NH3) = 1 mol/L c(HCl) = 0.1 mol/L Fill approx. 30 mL ultrapure water into a 50 mL volumetric flask. Carefully add 5.55 mL acetic acid (100 %), 3.7 mL NH3 (25 %) and 0.5 mL HCl (30 %). Make up to the mark with ultrapure water. 10 mg/L Cd standard solution β(Cd) = 10 mg/L Fill approx. 40 mL ultrapure water into a 50 mL volumetric flask. Add 50 µL concentrated HNO3 (65%) and 500 µL Cd standard stock solution (1 g/L). Make up to the mark with ultrapure water. 10 mg/L Pb standard solution β(Pb) = 10 mg/L Fill approx. 40 mL ultrapure water into a 50 mL volumetric flask. Add 50 µL concentrated HNO3 (65%) and 500 µL Pb standard stock solution (1 g/L). Make up to the mark with ultrapure water. Mixed standard 1 β(Cd) = 0.2 mg/L β(Pb) = 0.3 mg/L Fill approx. 40 mL ultrapure water into a 50 mL volumetric flask. Add 50 µL concentrated HNO3 (65%) 1 mL 10 mg/L Cd standard solution and 1.5 mL 10 mg/L Pb standard solution. Make up to the mark with ultrapure water. Mixed standard 2 β(Cd) = 0.5 mg/L β(Pb) = 1.0 mg/L Fill approx. 40 mL ultrapure water into a 50 mL volumetric flask. Add 50 µL concentrated HNO3 (65%) 2.5 mL 10 mg/L Cd standard solution and 5 mL 10 mg/L Pb standard solution. Make up to the mark with ultrapure water. * e.g. Merck suprapur® , Sigma-Aldrich TraceSelect® or equivalent
- 57. Quantification of cadmium and lead Electrochemistry – A workbook for 910 PSTAT mini 55 Extraction solution w(CH3COOH) = 4 % v/v Dilute 40 mL acetic acid with 960 mL ultrapure water. 9.2 Experiment 9.2.1 Preparation of the mercury film The mercury film can be plated in situ, but ex situ plating should be preferred since it significantly reduces the consumption of mercury for this application. Plating solution 11 mL Hg plating solution (β(Hg) = 20 mg/L) Plating parameters Figure 23: Parameters for the deposition of the mercury film at the carbon electrode (experiment 9.2). Plating a) Pipette 12 mL Hg plating solution into the measuring vessel. Put a stirrer bar into the measuring vessel and stir the solution well. b) Take a new carbon electrode (6.1208.110) and assemble it with the measuring vessel cover. Take care not to touch the active electrode surface with bare fingers. Immerse the electrode into the plating solution and close the measuring vessel. c) Make sure that the electrical contacts of the electrode are dry and free from contaminants. Then connect the electrode cable. d) Deposit the mercury film with the plating parameters from Figure 23. The stirrer has to be switched on during «tcond» and «tdep» but switched off during «tequil» and the potential scan. Usually a deposition of 5 minutes is sufficient to get a proper mercury film. Note! The Hg plating solution can be reused multiple times. If the solution cannot be used anymore take care of an appropriate disposal.
- 58. Quantification of cadmium and lead 56 Metrohm Monograph 8.108.5020EN 9.2.2 Deposition potential Measuring solution 10 mL H2O 1 mL buffer pH 4.4 0.1 mL Cd standard solution (β(Cd) = 10 mg/L) 0.1 mL Pb standard solution (β(Pb) = 10 mg/L) Voltammetric parameters Figure 24: Start parameters for the optimization of deposition potential (experiment 9.2). Measurement a) Plate a mercury film on a new carbon electrode (6.1208.110) as described in 9.2.1 Preparation of the mercury film. b) Rinse the electrode well with ultrapure water. Take care not to touch the mercury film with bare fingers. c) Prepare the measuring solution by pipetting 10 mL H2O, 1 mL buffer pH 4.4, 0.1 mL Cd standard solution (β(Cd) = 10 mg/L ) and 0.1 mL Pb standard solution (β(Pb) = 10 mg/L) into the measuring vessel. Put a stirrer bar into the measuring vessel and stir the solution well. d) With the measuring vessel cover assembled immerse the electrode into the measuring solution and close the measuring vessel. e) Make sure that the electrical contacts of the electrode are dry and free from contaminants. Then connect the electrode cable. f) Record the voltammogram with the voltammetric parameters from Figure 24. The stirrer has to be switched on during «tcond» and «tdep» but switched off during «tequil» and the whole potential scan. g) Save the voltammogram together with the method parameters. h) Change the deposition potential «Edep» to -0.6 V. Stir the solution. i) Record another voltammogram using the same electrode. The stirrer has to be switched on during «tcond» and «tdep» but switched off during «tequil» and the whole potential scan.
- 59. Quantification of cadmium and lead Electrochemistry – A workbook for 910 PSTAT mini 57 j) Save the voltammogram together with the method parameters. k) Repeat step h) to j) with deposition potentials of -0.7 V, -0.8 V, -0.9 V, -1.0 V, -1.2 V and -1.4 V. Evaluation l) Evaluate the peak height of the cadmium and the lead signals at the different deposition potentials as described in 9.2.6. m) Plot graphs of the peak height as a function of the deposition potential for both elements. n) What can be observed? Based on your observation choose a suitable deposition potential for the following experiments. 9.2.3 Linear working range Measuring solution 10 mL H2O 1 mL buffer pH 4.4 0.05 mL Cd standard solution (β(Cd) = 10 mg/L ) 0.05 mL Pb standard solution (β(Pb) = 10 mg/L) Voltammetric parameters Figure 25: Parameters for the determination of cadmium and lead at the mercury film electrode (experiment 9.2). Measurement a) Plate a mercury film on a new carbon electrode (6.1208.110) as described in 9.2.1 Preparation of the mercury film. b) Rinse the electrode well with ultrapure water. Take care not to touch the mercury film. c) Prepare the measuring solution by pipetting 10 mL H2O, 1 mL buffer pH 4.4, 0.05 mL Cd standard solution (β(Cd) = 10 mg/L) and 0.05 mL Pb standard solution (β(Pb) = 10 mg/L) into the measuring vessel. Put a stirrer bar into the measuring vessel and stir the solution well.
- 60. Quantification of cadmium and lead 58 Metrohm Monograph 8.108.5020EN d) With the measuring vessel cover assembled immerse the electrode into the measuring solution and close the measuring vessel. e) Make sure that the electrical contacts of the electrode are dry and free from contaminants. Then connect the electrode cable. f) Use the parameters optimized in experiment 9.2.2 or enter the voltammetric parameters given in Figure 25. g) Record the voltammogram. The stirrer has to be switched on during «tcond» and «tdep» but switched off during «tequil» and the whole potential scan. h) Save the voltammogram together with the method parameters. i) Add another 0.05 mL of each Cd standard solution (β(Cd) = 10 mg/L) and Pb standard solution (β(Pb) = 10 mg/L). Stir the solution well. j) Record another voltammogram using the same electrode and parameters. The stirrer has to be switched on during «tcond» and «tdep» but switched off during «tequil» and the whole potential scan. k) Save the voltammogram together with the method parameters. l) Repeat step i) to k) until you recorded curves for 8 to 10 different concentrations. Evaluation m) Evaluate the peak height of the cadmium and the lead signals for the individual concentrations as described in 9.2.6. n) Plot graphs with the peak height as a function of the concentration for both elements. o) From the graph determine the concentration range where there is a linear relation between concentration and peak height for both elements. 9.2.4 Limit of quantification In the literature many different approaches for the determination of the limit of determination (LOD) and the limit of quantification (LOQ) are described. The choice is from the simple consideration of the background noise as a measure for the sensitivity to rather complex statistical examinations of the error of the measurement, which requires numerous measuring. For practical application the so called «regression approach»(10) was found to be very useful. On the one hand it is easy to carry out, on the other hand it provides realistic values for the critical value or critical level (LC) and minimum quantifiable (true) value or quantification limit (LQ), as the LOD and the LOQ should be named according to IUPAC(11) . In principle the regression approach is a simplified statistical approach. It uses the residual standard deviation of a calibration curve recorded in the concentration range of the LOQ for the calculation. The calibration curve has to fulfill the following requirements: Linear relation between concentration and signal, calibration curve y = A + B x Blank measurement (c = 0) has to be included in the calibration curve 5 to 10 calibration standards, calibration points equidistant 5 to 10 replications per standard, same number of replications per standard Min. 40 measuring points for c ≠ 0 Lowest concentration in the range of LOQ Highest concentration 10 ... 30 * LOD Standard addition can be used to record the calibration curve Standard deviation is homogenous (homoscedastic) For the calculations the following rules should be considered: Blank signals (c = 0) are included in the calculation of the residual standard deviation . Blank signals (c = 0) are not included for the calculation of parameters A (intercept) and B (slope) of the linear regression.
- 61. Quantification of cadmium and lead Electrochemistry – A workbook for 910 PSTAT mini 59 Formulas y = A + B x (Eq. 5) y – Peak height x – Concentration of the analyte A – Intercept of the linear regression B – Slope of the linear regression ∑ ( ̂ ) (Eq. 6) – Standard error of estimate (residual standard deviation) in regression – Variance of – Signal value of the ith point in the regression ̂ – Regression value of the signal at the ith point of the linear regression – Number of points on the regression – Number of calibration standards – Number of regression parameters (for linear regression = 2) oncentration (Eq. 7) oncentration 10 (Eq. 8) Recording the calibration curve for the determination of LOQ Measuring solution 10 mL H2O 1 mL buffer pH 4.4 Standard addition 5 additions of 0.1 mL mixed standard solution 1 (β(Cd) = 0.2 mg/L, β(Pb) = 0.3 mg/L) each. Voltammetric parameters See Figure 25. Measurement a) Plate a mercury film on a new carbon electrode (6.1208.110) as described in 9.2.1 Preparation of the mercury film. b) Rinse the electrode well with ultrapure water. Take care not to touch the mercury film. c) Prepare the measuring solution by pipetting 10 mL H2O and 1 mL buffer pH 4.4 into the measuring vessel. Put a stirrer bar into the measuring vessel and stir the solution well. d) With the measuring vessel cover assembled immerse the electrode into the measuring solution and close the measuring vessel. e) Make sure that the electrical contacts of the electrode are dry and free from contaminants. Then connect the electrode cable. f) Use the parameters optimized in experiment 9.2.2 or enter the voltammetric parameters given in Figure 25.
- 62. Quantification of cadmium and lead 60 Metrohm Monograph 8.108.5020EN g) Record the voltammogram. The stirrer has to be switched on during «tcond» and «tdep» but switched off during «tequil» and the whole potential scan. h) Stir the solution and repeat the measurement of the blank (c = 0). In total 10 replications are required. i) Save the voltammograms together with the method parameters. j) Add 0.1 mL of the mixed standard solution (with β(Cd) = 0.2 mg/L and β(Pb) = 0.3 mg/L). Stir the solution well. k) Repeat the measurement for this concentration. The stirrer has to be switched on during «tcond» and «tdep» but switched off during «tequil» and the whole potential scan. In total 10 repetitive measurements of this standard are required. l) Save the voltammograms together with the method parameters. m) Repeat step j) to l) until you have recorded curves with 5 different concentrations. Evaluation n) Evaluate the peak height for the individual concentrations for both elements as described in 9.2.6. o) Plot a graph with the peak height as a function of the concentration for both elements. p) Calculate the linear regression of the calibration curve for both elements. q) Calculate the residual standard deviation of the calibration curve for both elements. r) Using the residual standard deviation calculate the LOD and the LOQ of the cadmium determination as well as the lead determination. 9.2.5 Determination of cadmium and lead in articles of daily use The working range of the determination of cadmium and lead with the described parameters is approximately in the low and middle ppb range. An interesting application in this concentration range is the analysis of cadmium and lead released from articles of daily use, such as ceramics, glassware, PVC tubes or baby toys. Sampling and limits for the release of cadmium and lead from glass ware in contact with food for example can be found in ISO 7086(17)(18) . To quantify the release of the metals the products are leached with w(acetic acid) = 4 % for 24 hours. Afterwards the concentration of cadmium and lead in this extraction solution is determined. The quantification is carried out by standard addition technique. Measuring solution 10 mL H2O 1 mL buffer pH 4.4 1 mL extraction solution Standard addition Concentration is quantified by 2 additions of 0.1 mL mixed standard solution 2 (β(Cd) = 0.5 mg/L, β(Pb) = 1.0 mg/L). Voltammetric parameters See Figure 25. Determination in the sample a) Plate a mercury film on a new carbon electrode (6.1208.110) as described in 9.2.1 Preparation of the mercury film.
- 63. Quantification of cadmium and lead Electrochemistry – A workbook for 910 PSTAT mini 61 b) Rinse the electrode well with ultrapure water. Take care not to touch the mercury film. c) Prepare the measuring solution «sample» by pipetting 10 mL H2O, 1 mL buffer pH 4.4 and 1 mL extraction solution into the measuring vessel. Put a stirrer bar into the measuring vessel and stir the solution well. d) With the measuring vessel cover assembled immerse the electrode into the measuring solution and close the measuring vessel. e) Make sure that the electrical contacts of the electrode are dry and free from contaminants. Then connect the electrode cable. f) Use the parameters optimized in experiment 9.2.2 or enter the voltammetric parameters given in Figure 25. g) Record the voltammogram. The stirrer has to be switched on during «tcond» and «tdep» but switched off during «tequil» and the whole potential scan. h) Save the voltammogram together with the method parameters. i) Add 0.1 mL of the mixed standard solution 2 (β(Cd) = 0.5 mg/L, β(Pb) = 1.0 mg/L). Stir the solution. j) Record another voltammogram using the same electrode and parameters. The stirrer has to be switched on during «tcond» and «tdep» but switched off during «tequil» and the whole potential scan. k) Save the voltammogram together with the method parameters. l) Add another 0.1 mL of the mixed standard solution 2 (β(Cd) = 0.5 mg/L, β(Pb) = 1.0 mg/L). Stir the solution. m) Record another voltammogram using the same electrode and parameters. The stirrer has to be switched on during «tcond» and «tdep» but switched off during «tequil» and the whole potential scan. n) Save the voltammogram together with the method parameters. Concentration evaluation o) Evaluate the peak heights for cadmium and lead for the sample and the two standard additions as described in 9.2.6. p) Plot a graph with peak height as a function of concentration for cadmium and lead. The concentration in the sample is set to zero. q) Calculate the linear regression for the standard addition curve. r) Extrapolate the linear regression onto the x-axis (concentration axis) to get the negative concentration of cadmium and lead in the measuring solution. Calculate the concentration of cadmium and lead in the extraction solution from this value.
- 64. Quantification of cadmium and lead 62 Metrohm Monograph 8.108.5020EN 9.2.6 Curve evaluation For the evaluation of the peak height «peak measurement tool 1» can be used. Peak potential of cadmium is approx. -0.8 V Peak potential of lead is approx. -0.6 V Figure 26: Example for the evaluation of peak height of cadmium and lead (both approx 90 µg/L) in experiment 9.2. 9.2.7 Additional information Note! The Hg plating solution can be reused multiple times. If the solution cannot be used anymore take care of an appropriate disposal. Cadmium and lead are toxic to the environment. Their standard solutions should be disposed appropriately as well. The lifetime of the mercury film at the carbon electrode is limited. If measurements are done in clean standard solutions several measurements at the same electrode are possible. A calibration curve for example can be recorded using just one electrode. As soon as the matrix of a real sample is involved the lifetime decreases. For samples approx. 3 to 5 determinations including the standard additions are possible. The mercury film cannot be removed to plate a fresh film at the same electrode, therefore it is recommended to plate a new mercury film only on a new electrode. The performance of the determination also depends on the quality of the mercury film. Problems with the linearity of the calibration curve for example can be related to the quality of the mercury film. In this case increase the plating time for the preparation of the mercury film from 5 minutes to 10 minutes.
- 65. The principle of a glucose sensor Electrochemistry – A workbook for 910 PSTAT mini 63 10 The principle of a glucose sensor Amperometric detection of glucose at an enzyme modified platinum electrode The glucose sensor is one of the great success stories in the field of biosensors, from one of the first publications of the principle by Updike and Hicks(19) in 1967, millions of this kind of sensors are sold today for monitoring blood glucose. The principle is both simple and brilliant. It is based on the oxidation of glucose to glucono lactone and hydrogen peroxide catalyzed by the enzyme glucose oxidase. The hydrogen peroxide produced in this reaction is then determined in an amperometric measurement. Figure 27: Principle of a glucose sensor In this experiment a simple glucose sensor will be manufactured. Its function will be tested in a flow injection system by measuring the glucose content of different food products such as honey, fruit juices and beverages. The determination is carried out by amperometric detection. For further reading on the principle of the glucose sensor see e.g. Bond, Broadening Electrochemical Horizons (5) . 10.1.1 Accessories 910 PSTAT mini Electrode cable 6.2163.000 Electrode 6.1208.510 (WE – Pt, AE – C, RE – Ag) Additional accessories (not included in the scope of delivery of the 910 PSTAT mini) Flow cell for screen printed electrodes (e.g. DropSens DRP-FLWCL) Peristaltic pump 6-port injection valve with 0.5 mL sample loop Capillary tubings (PEEK or PTFE with inner diameter in the range of 0.5 … 0.9 mm) Pipettes Volumetric flasks Figure 28: Flow cell (open) with electrode 6.1208.510 Pt electrode 2 e- 2 H+ + O2 Gluconolactone + H2O2 Glucose + O2 GOx immobilized glucose oxidase (GOx) Sample solution
- 66. The principle of a glucose sensor 64 Metrohm Monograph 8.108.5020EN 10.1.2 Reagents Potassium dihydrogen phosphate, for analysis, KH2PO4, CAS 7778-77-0 Sodium hydrogen phosphate, for analysis, Na2HPO4, CAS 7558-79-4 Potassium chloride, for analysis, KCl, CAS 7447-40-7 Glucose oxidase (GOx), 192000 units/gram, CAS 9001-37-0 Nafion 117 solution, ~5% in a mixture of lower aliphatic alcohols and water, CAS 31175-20-9 D-(+)-Glucose anhydrous, C6H12O6, CAS 50-99-7 Ultrapure water type 1 (electrical resistivity > 18.2 MΩ·cm, TOC < 10 ppb) Only for 10.2.4 Interferences: D-(-)-fructose, C6H12O6, CAS 57-48-7 D-(+)-galactose, C6H12O6, CAS 59-23-4 D-(+)-mannose, C6H12O6, CAS 3458-28-4 Sucrose, C12H22O11, CAS 57-50-1 Vitamin C (ascorbic acid), puriss. p.a., C6H8O6, CAS 50-81-7 Ready-to-use solutions Phosphate buffer pH 5.2 c(KH2PO4) = 0.06 mol/L c(Na2HPO4) = 0.007 mol/L c(KCl) = 0.1 mol/L Weigh in 8.1654 g KH2PO4, 0.9937 g Na2HPO4 and 7.4551 g KCl and transfer everything into a 1 L volumetric flask. Dissolve and make up to the mark with ultrapure water. The solution has approx. pH 5.2. GOx stock solution c(GOx) ~ 3500 units/mL Dissolve 2.8 mg glucose oxidase in 150 µL phosphate buffer pH 5.2. When the solution is not used store it in the refrigerator.. Glucose stock solution β(glucose) = 10 g/L Weigh in 0.50 g D-(+)-glucose anhydrous and transfer it into a 50 mL volumetric flask. Dissolve and make up to the mark with phosphate buffer pH 5.2. Glucose standard solution β(glucose) = 50 mg/L Pipette 0.05 mL glucose stock solution (β(glucose) = 10 g/L) into a 10 mL volumetric flask. Make up to the mark with phosphate buffer pH 5.2. β(glucose) = 100 mg/L Prepare as described above, but use 0.1 mL glucose stock solution (β(glucose) = 10 g/L) instead. β(glucose) = 200 mg/L Use 0.2 mL glucose stock solution (β(glucose) = 10 g/L) β(glucose) = 300 mg/L Use 0.3 mL glucose stock solution (β(glucose) = 10 g/L) β(glucose) = 400 mg/L Use 0.4 mL glucose stock solution (β(glucose) = 10 g/L) β(glucose) = 500 mg/L
- 67. The principle of a glucose sensor Electrochemistry – A workbook for 910 PSTAT mini 65 Use 0.5 mL glucose stock solution (β(glucose) = 10 g/L) β(glucose) = 600 mg/L Use 0.6 mL glucose stock solution (β(glucose) = 10 g/L) β(glucose) = 800 mg/L Use 0.8 mL glucose stock solution (β(glucose) = 10 g/L) β(glucose) = 1000 mg/L Use 1.0 mL glucose stock solution (β(glucose) = 10 g/L) Only for 10.2.4 Interferences: Fructose stock solution β(fructose) = 10 g/L Weigh in 0.1 g D-(-)-fructose and transfer it into a 10 mL volumetric flask. Dissolve and make up to the mark with phosphate buffer pH 5.2. Fructose standard solution β(fructose) = 400 mg/L Pipette 0.4 mL fructose stock solution (β(fructose) = 10 g/L) into a 10 mL volumetric flask. Make up to the mark with phosphate buffer pH 5.2. Galactose stock solution β(galactose) = 10 g/L Weigh in 0.1 g D-(+)-galactose and transfer it into a 10 mL volumetric flask. Dissolve and make up to the mark with phosphate buffer pH 5.2. Galactose standard solution β(galactose) = 400 mg/L Pipette 0.4 mL galactose stock solution (β(galactose) = 10 g/L) into a 10 mL volumetric flask. Make up to the mark with phosphate buffer pH 5.2. Mannose stock solution β(mannose) = 10 g/L Weigh in 0.1 g D-(+)-mannose and transfer it into a 10 mL volumetric flask. Dissolve and make up to the mark with phosphate buffer pH 5.2. Mannose standard solution β(mannose) = 400 mg/L Pipette 0.4 mL mannose stock solution (β(mannose) = 10 g/L) into a 10 mL volumetric flask. Make up to the mark with phosphate buffer pH 5.2. Sucrose stock solution β(sucrose) = 10 g/L Weigh in 0.1 g sucrose and transfer it into a 10 mL volumetric flask. Dissolve and make up to the mark with phosphate buffer pH 5.2. Sucrose standard solution β(sucrose) = 400 mg/L Pipette 0.4 mL mannose stock solution (β(sucrose) = 10 g/L) into a 10 mL volumetric flask. Make up to the mark with phosphate buffer pH 5.2. Vitamin C stock solution β(vitamin C) = 10 g/L Weigh in 0.1 g vitamin C and transfer it into a 10 mL volumetric flask. Dissolve and make up to the mark with phosphate buffer pH 5.2. Vitamin C standard solution β(vitamin C) = 10 mg/L Pipette 0.01mL vitamin C stock solution (β(vitamin C) = 10 g/L) into a 10 mL volumetric flask. Make up to the mark with phosphate buffer pH 5.2.
- 68. The principle of a glucose sensor 66 Metrohm Monograph 8.108.5020EN 10.2 Experiment 10.2.1 Setup of the flow injection system Figure 29: Schematic setup of the flow injection system. Working conditions Tubing connections PEEK or PTFE capillary tubings with an inner diameter in the range of 0. … 0.9 mm Sample loop 0.5 mL Flow rate 0.9 mL/min Carrier solution Phosphate buffer pH 5.2 10.2.2 Preparation of GOx modified electrode GOx coating solution 80 µL GOx stock solution (c(GOx) ~ 3500 units/mL) 20 µL Nafion 117 solution Coating a) Prepare the GOx coating solution by thoroughly mixing of 80 µL GOx stock solution (c(GOx) ~ 3500 units/mL) and 20 µL Nafion 117 solution. b) Pipette 2 µL of the GOx coating solution on the platinum electrode (6.1208.510). The droplet should be positioned in the middle of the working electrode area. Take care not to coat the reference and the auxiliary electrode. c) Let the electrode air dry for 10 to 20 min. d) Pipette 2 µL nafion 117 solution (w(nafion) ~ 5 %) on top of the GOx coating. Take care not to coat the reference and the auxiliary electrode. e) Let the electrode air dry for 10 to 20 min. f) Before use immerse the electrode in the phosphate buffer for approx. 30 min.
- 69. The principle of a glucose sensor Electrochemistry – A workbook for 910 PSTAT mini 67 g) Install the GOx modified electrode in the flow cell. Take care not to touch the active electrode surface with bare fingers. h) Flush the flow cell with the phosphate buffer pH 5.2 and make sure that the flow cell and all tubing connections are free from air bubbles. i) Make sure that the electrical contacts of the electrode are dry and free from contaminants. Then connect the electrode cable. Now the system is ready to use. 10.2.3 Linear working range Standard solutions β(glucose) = 200 mg/L β(glucose) = 400 mg/L β(glucose) = 600 mg/L β(glucose) = 800 mg/L β(glucose) = 1000 mg/L Voltammetric parameters Figure 30: Parameters for the determination of glucose on a GOx modified electrode (experiment 10.2). Measurement a) Prepare the 5 glucose standard solutions of β(glucose) = 200 mg/L, 400 mg/L, 600 mg/L, 800 mg/L and 1000 mg/L by the dilution of the appropriate amount of glucose standard stock solution (β(glucose) = 10 g/L) with the phosphate buffer pH 5.2. b) Start the peristaltic pump. Make sure that the phosphate buffer shows a steady flow without pulsation. c) Start the data recording with the parameters given in Figure 30. d) Fill the sample loop with glucose standard solution β(glucose) = 200 mg/L. e) When the current of the amperometric measurement is stable, inject the standard solution. f) Wait until the standard solution has passed the flow cell. This is indicated by the current which returns to the initial value before the injection. Then fill the sample loop again with the standard solution.
- 70. The principle of a glucose sensor 68 Metrohm Monograph 8.108.5020EN g) Repeat the injection of glucose standard solution β(glucose) = 200 mg/L. In total 3 to 5 injections of the standard should be done. After the last injection stop the data recording. h) Repeat step c) to g) also for the other standard solutions. Use β(glucose) = 400 mg/L, 600 mg/L, 800 mg/L and 1000 mg/L instead in step d) and f). Evaluation i) Evaluate the peak area of the glucose signals as described in 10.2.6. For each concentration calculate the mean value from the repeated injections. j) Plot a graph with the averaged peak area as a function of the concentration. k) From the graph determine the concentration range where there is a linear relation between concentration and peak area. 10.2.4 Interferences Before determining the concentration of glucose in food products, check for possible interferences from e.g. other monosaccharides such as fructose, galactose or mannose or from the common disaccharide sucrose which consists of one molecule fructose and one molecule glucose. Also the interference of vitamin C, which is present in many fruit juices either naturally or as antioxidant, should be tested. Standard solutions β(glucose) = 400 mg/L β(galactose) = 400 mg/L β(mannose) = 400 mg/L β(sucrose) = 400 mg/L β(vitamin C) = 10 mg/L Voltammetric parameters See Figure 30. Measurement a) Prepare the glucose standard solution of β(glucose) = 400 mg/L by diluting the glucose standard stock solution (β(glucose) = 10 g/L) with the phosphate buffer pH 5.2. b) Prepare the fructose standard solution of β(fructose) = 400 mg/L by diluting the fructose standard stock solution (β(fructose) = 10 g/L) with the phosphate buffer pH 5.2. c) Start the peristaltic pump. Make sure that the phosphate buffer shows a steady flow without pulsation. d) Start the data recording with the parameters given in Figure 30. e) Fill the sample loop with glucose standard solution β(glucose) = 400 mg/L. f) When the current of the amperometric measurement is stable, inject the glucose standard solution. g) Wait until the standard solution has passed the flow cell. This is indicated by the current which returns to the initial value before the injection. h) Fill the sample loop with fructose standard solution β(fructose) = 400 mg/L. i) When the current of the amperometric measurement is stable, inject the fructose standard solution. j) Stop the data recording when you are sure that the fructose standard solution has passed the flow cell.
- 71. The principle of a glucose sensor Electrochemistry – A workbook for 910 PSTAT mini 69 k) Repeat step b) to j) also for the other standard solutions. Prepare β(galactose) = 400 mg/L, β(mannose) = 400 mg/L, β(sucrose) = 400 mg/L or β(vitamin C) = 10 mg/L in step b) and use the corresponding standard in step h). Evaluation l) Compare the signal for the glucose standard (β(glucose) = 400 mg/L) with the signals of the other tested standard solutions. Decide which substances will interfere. Keep possible interferences in mind when selecting samples for experiment 10.2.5. 10.2.5 Determination of glucose in different food products Many food products contain sugar. However, how much of this sugar is glucose, which plays an important role in the catabolism of humans and other living organism? Food products containing glucose are fruit juices, such as grape juice or apple juice and beverages such as iced tea or cola soft drink. Honey typically contains between 22 % and 41 % glucose. The quantification of glucose requires a calibration. Record a calibration curve and carry out the determinations in the different samples using this calibration curve. To verify the results check the recovery in one sample. Sample solutions Juice or beverage sample solution Pipette 0.1 mL of the sample into a 10 mL volumetric flask. Make up to the mark with phosphate buffer pH 5.2. Honey stock solution Weigh out 1.0 g of the sample and transfer it into a 25 mL volumetric flask. Add approx. 20 mL phosphate buffer and mix until the honey is completely dissolved. Make up to the mark with phosphate buffer pH 5.2. Honey sample solution Pipette 0.1 mL of the honey stock solution into a 10 mL volumetric flask. Make up to the mark with phosphate buffer pH 5.2. Recovery test solution Pipette 0.1 mL of the honey stock solution and 0.1 mL of the glucose stock solution (β(glucose) = 10 g/L) into a 10 mL volumetric flask. Make up to the mark with phosphate buffer pH 5.2. Note! The volume of glucose stock solution might need to be adapted depending on the concentration in the sample. See also the additional information on the recovery in chapter 10.2.7. Calibration standard solutions β(glucose) = 50 mg/L β(glucose) = 100 mg/L β(glucose) = 200 mg/L β(glucose) = 300 mg/L β(glucose) = 400 mg/L β(glucose) = 500 mg/L β(glucose) = 600 mg/L Voltammetric parameters See Figure 30.
- 72. The principle of a glucose sensor 70 Metrohm Monograph 8.108.5020EN Recording the calibration curve a) Prepare the glucose standard solutions of β(glucose) = 50 mg/L, 100 mg/L, 200 mg/L, 300 mg/L, 400 mg/L, 500 mg/L and 600 mg/L by the dilution of the appropriate amount of glucose standard stock solution (β(glucose) = 10 g/L) with the phosphate buffer pH 5.2. b) Start the peristaltic pump. Make sure that the phosphate buffer shows a steady flow without pulsation. c) Start the data recording with the parameters given in Figure 30. d) Fill the sample loop with glucose standard solution β(glucose) = 50 mg/L. e) When the current of the amperometric measurement is stable, inject the standard solution. f) Wait until the standard solution has passed the flow cell. This is indicated by the current which returns to the initial value before the injection. Then fill the sample loop again with the standard solution. g) Repeat the injection of glucose standard solution β(glucose) = 50 mg/L. In total 3 to 5 injections of the standard should be done. After the last injection stop the data recording. h) Repeat step c) to g) also for the other standard solutions. Use β(glucose) = 100 mg/L, 200 mg/L, 300 mg/L, 400 mg/L, 500 mg/L or 600 mg/L instead in step d) and f). Establishing the calibration curve i) Evaluate the peak area of the glucose signals as described in 10.2.6. For each concentration calculate the mean value from the repeated injections. j) Plot a graph with the averaged peak area as a function of the concentration and calculate the linear regression for the calibration curve. Determination in the sample k) Start the data recording with the parameters given in Figure 30. l) Fill the sample loop with the sample solution (e. g. honey diluted in phosphate buffer pH 5.2). m) When the current of the amperometric measurement is stable, inject the sample solution. n) Wait until the sample solution has passed the flow cell. This is indicated by the current, which returns to the initial value before the injection. Then fill the sample loop again with the sample solution. o) Repeat the injection of sample solution. In total 3 to 5 injections of the sample should be done. After the last injection stop the data recording. p) Repeat step k) to o) also with the recovery test solutions and the other sample solutions. Concentration evaluation q) Evaluate the peak area of the glucose signals as described in 10.2.6. For each sample calculate the mean value from the repeated injections. r) Compare the averaged peak area with the calibration curve and calculate the concentration in the diluted sample. s) From this value calculate the concentration of glucose in the undiluted sample and the recovery for the recovery test solutions.
- 73. The principle of a glucose sensor Electrochemistry – A workbook for 910 PSTAT mini 71 10.2.6 Curve evaluation For the evaluation of the peak area «peak measurement tool 1» can be used. The peak area corresponds to the charge stated on the tab «Measurements». Figure 31: Example for the evaluation of the peak area of the glucose signal (3 injections of β(glucose) = 400 mg/L each) in experiment 10.2. 10.2.7 Additional information A GOx coated electrode can be stored dry for a few days. When the electrode is not in use, e.g. over night, take it out of the flow cell, rinse it carefully with ultrapure water, let it air dry and store it dry. The sensitivity of the determination depends on the amount of GOx immobilized at the electrode. Therefore only measurements can be compared which have been done on electrodes coated with the same procedure using the same GOx coating solution. Furthermore the sensitivity decreases over time. For this reason the calibration curve should be checked from time to time by measuring a standard solution with a known concentration. Instead of the peak area it is also possible to evaluate the peak height. The application will show similar results. For the preparation of the recovery test solution the concentration in the sample should be increased by 50 % to 100 %. The recovery is then calculated with respect to the spiked amount. ( ) With – concentration in the recovery test solution – concentration in the sample solution – spiked concentration
- 75. Examples Electrochemistry – A workbook for 910 PSTAT mini 73 11 Examples
- 77. Examples Electrochemistry – A workbook for 910 PSTAT mini 75 Experiment 2: Standard reduction potential Measuring data and evaluation Pb Eobs = -0.68 V E0 = -0.13 V Pb2+ (aq) + 2 e- ⇌ Pb(s) Cu Eobs = -0.41 V E0 = +0.34 V Cu2+ (aq) + 2 e- ⇌ Cu(s) Bi Eobs = -0.28 V E0 = +0.308 V Bi3+ (aq) + 3 e- ⇌ Bi(s)
- 78. Experiment 2: Standard reduction potential 76 Metrohm Monograph 8.108.5020EN Hg Eobs = -0.01 V E0 = +0.85 V Hg2+ (aq) + 2 e- ⇌ Hg(l) Au Eobs = +0.33 V E0 = +0.93 V [AuCl4]- (aq) + 3 e- ⇌ Au(s) + 4 Cl- Figure 32: Linear sweep voltammograms of different metal ions (gray line – supporting electrolyte, black line – c(metal) = 0.18 mmol/L in the supporting electrolyte). Eobs – observed reduction potential, E0 – standard reduction potential (20) . Result discussion When the metals are sorted by their reduction potential it can be seen that precious metals like gold have the more positive potential, means they can more easily be reduced to their metallic form. Base metals like lead have a more negative potential and can therefore more easily be oxidized to their ionic form. Base metal Precious metal Negative reduction potential Positive reduction potential Figure 33: Lead, copper, bismuth, mercury and gold sorted by their reduction potentials. Pb2+ -0.68 V Cu2+ -0.41 V Bi3+ -0.28 V Hg2+ -0.01 V Au3+ +0.33 V + –
- 79. Examples Electrochemistry – A workbook for 910 PSTAT mini 77 The differences between the observed reduction potential and the standard reduction potential can be explained by the differences in the experimental setup. For the measurement of the standard reduction potential a metal cathode is immersed into a 1 molar solution of the corresponding metal ion. The resulting potential at equilibrium is measured against a reference electrode. In contrast to the measurement of the standard reduction potential experiment 2 is carried out under potentiodynamic conditions. The reaction at the electrode is driven by an externally applied voltage which is continuously changed. Another important difference is the reference electrode. Potentials cannot be measured as absolute potentials but as potential difference between two electrodes. In electrochemical experiments the potential difference is measured between the reference electrode, which provides a stable potential, and the working electrode, where the electrochemical reaction takes place. As a consequence the displayed potential depends on the reference electrode used for the experiment. The values for the standard reduction potential are specified with respect to the standard hydrogen electrode (SHE), whereas in this experiment the reference electrode is metallic silver. Despite the offset between the tabled value for the standard reduction potentials and the observed reduction potentials the experiment allows a good differentiation between precious and base metals.
- 81. Examples Electrochemistry – A workbook for 910 PSTAT mini 79 Experiment 3: A reversible redox system Measuring data and evaluation Anodic Cathodic / V·s-1 / V / µA / V / µA 0.01 0.068 1.882 0.000 -1.805 0.02 0.060 2.672 0.000 -2.540 0.03 0.056 3.258 -0.004 -3.087 0.04 0.056 3.765 -0.008 -3.546 0.05 0.052 4.204 -0.012 -3.915 / V·s-1 / mV | ⁄ | 0.01 68 1.04 0.02 60 1.05 0.03 60 1.06 0.04 64 1.06 0.05 64 1.07 Figure 34: Cyclic voltammograms of c(p-aminophenol) = 0.09 mmol/L with scan rate of 10, 20, 30, 40 and 50 mV/s Result discussion At scan rates between 10 and 50 mV·s-1 p-aminophenol fulfills the criteria of a reversible reaction. The peak height increases with increasing sweep rate and the peak heights for the anodic and the cathodic signal are almost equal. The peak potentials for the anodic and cathodic signal slightly shift to negative potentials with increasing sweep rate, but the potential difference between the two signals is constant at 64 mV ± 4 mV. Considering the experimental setup (e.g. no IR drop compensation) this potential difference suggests a reaction with the transfer of one electron. A possible reaction mechanism could be as follows: p-AP p-AP + 1 e- + 1 H+ Reduced species Oxidized species Figure 35: Potential mechanism for the redox reaction of p-aminophenol. NH2 OH O NH2 e H + + +
- 82. Experiment 3: A reversible redox system 80 Metrohm Monograph 8.108.5020EN Calculation of the diffusion coefficient Randles-Sevcik equation √ (Eq. 3) With = 96480 C·mol-1 = 8.314 J·mol-1 ·K-1 = 298 K √ (Eq. 9) And = 1 = 0.09 mmol·L-1 = 9·10-8 mol·cm-3 = (4 mm/2)2 · = 0.1256 cm2 √ (Eq. 10) Figure 36: Peak height of anodic and cathodic peak of cyclic voltammograms of c(p-aminophenol) = 0.09 mmol/L plotted versus the square root of the scan rate. / V·s-1 √( s 1) / A / A 0.01 0.10 1.88·10-6 -1.81·10-6 0.02 0.14 2.67·10-6 -2.54·10-6 0.03 0.17 3.26·10-6 -3.09·10-6 0.04 0.20 3.77·10-6 -3.55·10-6 0.05 0.22 4.20·10-6 -3.92·10-6 slope 1.88·10-5 -1.71·10-5 Transforming (Eq. 10) √ √ slope = 3.81·10-5 cm2 ·s-1 = 3.17·10-5 cm2 ·s-1 -5 -4 -3 -2 -1 0 0 1 2 3 4 5 0.10 0.15 0.20 Ip,c / µA Ipa,, / µA √( / V·s-1) anodic cathodic Linear (anodic) Linear (cathodic)
- 83. Examples Electrochemistry – A workbook for 910 PSTAT mini 81 Experiment 4: A quasi-reversible redox system Measuring data and evaluation Anodic Cathodic / V·s-1 / V / µA / V / µA 0.1 0.054 5.795 -0.022 -5.172 0.2 0.054 8.182 -0.026 -6.972 0.3 0.058 9.507 -0.034 -7.910 0.4 0.058 11.207 -0.042 -9.007 0.5 0.062 12.395 -0.046 -9.746 / V·s-1 / mV | ⁄ | 0.1 76 1.12 0.2 80 1.17 0.3 92 1.20 0.4 100 1.24 0.5 108 1.27 Figure 37: Cyclic voltammograms of c(p-aminophenol) = 0.09 mmol/L with scan rate of 100, 200, 300, 400 and 500 mV/s. Result discussion At scan rates between 0.1 and 0.5 V/s the peak heights are still proportional to √ , but the peak heights of the anodic signal and the cathodic signal are not completely equal anymore. However, the most obvious indication that the process is not completely reversible anymore is the separation of anodic and cathodic peak potential. The difference of the peak potentials is significantly bigger than 59 mV and the separation of the two signals increases with faster scan rates. Therefore the reaction of p-aminophenol at higher scan rates can be considered to be quasi- reversible. Calculation of the standard rate constant for electron transfer The following reaction is assumed for the calculation p-AP p-AP + 1 e- + 1 H+ Reduced species Oxidized species Charge transfer parameter 𝜓 𝜓 √ (Eq. 4) By transforming (Eq. 4) the standard rate constant can be calculated as 𝜓 √ √ (Eq. 11)
- 84. Experiment 4: A quasi-reversible redox system 82 Metrohm Monograph 8.108.5020EN With the diffusion coefficients from experiment 3: = 3.81·10-5 cm2 ·s-1 = 3.17·10-5 cm2 ·s-1 and = 0.5 √ 1.10 (Eq. 12) 1.0 (Eq. 13) With = 1 = 96480 C·mol-1 = 8.314 J·mol-1 ·K-1 = 298 K 8.9 1 (Eq. 14) With the values from (Eq. 13) and (Eq. 14) the equation for standard rate constant (Eq. 11) can be written as 𝜓 √ (Eq. 15) (a) * † / mV 20 61 7 63 6 64 5 65 4 66 3 68 2 72 1 84 0.75 92 0.5 105 0.35 121 0.25 141 0.1 212 (b) Figure 38: Variation of peak potential separations with kinetic parameters for cyclic voltammetry. (a) table (b) semi-logarithmic plot of the tabl values (7) / V·s-1 √ / mV / cm·s-1 0.1 0.32 76 1.50 0.031 0.2 0.45 80 1.21 0.035 0.3 0.55 92 0.75 0.027 0.4 0.63 100 0.57 0.024 0.5 0.71 108 0.47 0.022 * See (Eq. 4) † For = 0.5 50 70 90 110 130 150 170 190 210 230 0.1 1 10 D E p ·n / mV
- 85. Examples Electrochemistry – A workbook for 910 PSTAT mini 83 Experiment 5: An irreversible redox system Measuring data and evaluation Anodic Cathodic / V·s-1 / V / µA / V / µA 0.05 0.325 24.283 -- -- 0.10 0.340 33.217 -- -- 0.15 0.350 40.104 -- -- 0.20 0.360 46.167 -- -- 0.25 0.365 51.441 -- -- Figure 39: Cyclic voltammograms of c(vitamin C) = 0.9 mmol/L with scan rate of 50, 100, 150, 200 and 250 mV/s. Result discussion Vitamin C shows the typical cyclic voltammogram for an irreversible process. The most obvious indication is the absence of a cathodic reduction signal. Furthermore the oxidation signals significantly shift to more positive potentials with faster scan rates. The most likely mechanism of the observed reaction is the oxidation of ascorbic acid to dehydroascorbic acid. Figure 40: Oxidation of vitamin C. O OH O H O O H O H H + e O O O H O H O O - 2 - 2
- 87. Examples Electrochemistry – A workbook for 910 PSTAT mini 85 Experiment 6: SAM – Self-assembled monolayers Figure 41: Example for curves obtained for the electrochemical conditioning of the gold electrodes. Measuring data and evaluation Coating Formula No. of C atoms / µA / µA 2-MAA HS(CH2)1COOH 1 -17.415 16.372 3-MPA HS(CH2)2COOH 2 -16.641 15.802 6-MHA HS(CH2)5COOH 5 -16.144 15.732 11-MUA HS(CH2)10COOH 10 -8.943 10.648 Figure 42: Cyclic voltammograms of gold electrodes coated with 2-MAA, 3-MPA, 6-MHA and 11-MUA (measuring solution: c(hexacyanoferrate(III)) = 1.5 mmol/L in c(acetate buffer) = 0.1 mol/L). Result discussion The graph in Figure 42 shows that there is an effect of the monolayer on the redox behavior Fe(III)/Fe(II) in the hexacyanoferrate complex. The signals become smaller the longer the molecule used for the coating. That means that the electrode is not just insulated by the coating, but the shielding depends on the thickness of the monolayer. -20 -16 -12 -8 -4 0 0 4 8 12 16 20 0 2 4 6 8 10 Ip,c / µA Ip,a / µA No. of C atoms in the spacer group anodic cathodic Linear (cathodic)
- 89. Examples Electrochemistry – A workbook for 910 PSTAT mini 87 Experiment 7: Quantification of vitamin C 7.2.1 Linear working range Concentration standard: β(vitamin C) = 10 g/L / mL / mL β(vitamin C) / mg·L-1 * / µA 0.02 11.02 18.1 0.690 0.04 11.04 36.2 1.323 0.06 11.06 54.2 1.936 0.08 11.08 72.2 2.510 0.10 11.10 90.1 2.997 0.12 11.12 107.9 3.478 0.14 11.14 125.7 3.991 0.16 11.16 143.4 4.451 0.18 11.18 161.0 4.927 0.20 11.20 178.6 5.366 * Mean of 2 replications. Concentrations outside the linear working range are marked gray. Figure 43: Linear working range for the determination of vitamin C. (Measuring solution: 10 mL H2O + 1 mL ammonium acetate buffer + ). Figure 44: Linear working range for the determination of vitamin C. 0 1 2 3 4 5 6 0 50 100 150 200 I p / µA c(vitamin C) / mg·L-1 Linear working range
- 90. Experiment 7: Quantification of vitamin C 88 Metrohm Monograph 8.108.5020EN 7.2.2 Limit of quantification Calibration curve for the determination of LOD and LOQ Figure 45: Example for curves recorded for the determination of LOD and LOQ of vitamin C. (Measuring solution: 10 mL H2O + 1 mL ammonium acetate buffer + ). Concentration standard: β(vitamin C) = 1 g/L Solution / mL / mL β(vitamin C) / µg·L-1 * / µA ̂ / µA Blank 0.000 11.000 0.0 0.004 0.003 Standard 1 0.025 11.025 2.3 0.081 0.090 Standard 2 0.050 11.050 4.5 0.180 0.176 Standard 3 0.075 11.075 6.8 0.272 0.262 Standard 4 0.100 11.100 9.0 0.350 0.347 Standard 5 0.125 11.125 11.2 0.424 0.432 * Mean of 10 replications Linear regression: y = A + B·x Regression parameters: Intercept (A) 0.003 µA Slope (B) 0.038 µA·L·mg-1 Calculation of the residual standard deviation ∑ ( ̂ ) (Eq. 6) 0.00 0.10 0.20 0.30 0.40 0.0 2.0 4.0 6.0 8.0 10.0 Ip / µA Concentration / mg·L-1
- 91. Examples Electrochemistry – A workbook for 910 PSTAT mini 89 Solution β(vitamin C) / mg·L-1 / µA ̂ / µA ̂ ( ̂ ) Blank 0.0 0.003 0.004 0.003 0.006 0.002 0.001 0.006 0.001 0.001 0.003 0.003 0.000 0.001 0.000 0.003 -0.001 -0.002 0.003 -0.002 -0.002 0.000 6.67E-08 5.50E-07 6.67E-08 7.52E-06 1.58E-06 5.10E-06 7.52E-06 5.10E-06 5.10E-06 6.67E-08 Standard 1 2.3 0.078 0.080 0.082 0.083 0.081 0.083 0.082 0.081 0.082 0.083 0.090 -0.012 -0.010 -0.008 -0.007 -0.009 -0.007 -0.008 -0.009 -0.008 -0.007 1.39E-04 9.57E-05 6.06E-05 4.60E-05 7.72E-05 4.60E-05 6.06E-05 7.72E-05 6.06E-05 4.60E-05 Standard 2 4.5 0.178 0.177 0.182 0.184 0.179 0.183 0.183 0.182 0.181 0.183 0.176 0.002 0.001 0.006 0.008 0.003 0.007 0.007 0.006 0.005 0.007 4.33E-06 1.17E-06 3.70E-05 6.53E-05 9.49E-06 5.01E-05 5.01E-05 3.70E-05 2.58E-05 5.01E-05 Standard 3 6.8 0.272 0.272 0.274 0.272 0.271 0.274 0.273 0.270 0.271 0.272 0.262 0.010 0.010 0.012 0.010 0.009 0.012 0.011 0.008 0.009 0.010 1.07E-04 1.07E-04 1.52E-04 1.07E-04 8.71E-05 1.52E-04 1.28E-04 6.95E-05 8.71E-05 1.07E-04 Standard 4 9.0 0.353 0.350 0.350 0.348 0.348 0.345 0.348 0.350 0.350 0.344 0.347 0.006 0.003 0.003 0.001 0.001 -0.002 0.001 0.003 0.003 -0.003 3.57E-05 8.84E-06 8.84E-06 9.48E-07 9.48E-07 4.11E-06 9.48E-07 8.84E-06 8.84E-06 9.16E-06 Standard 5 11.2 0.427 0.424 0.423 0.420 0.424 0.422 0.421 0.421 0.422 0.415 0.432 -0.005 -0.008 -0.009 -0.012 -0.008 -0.010 -0.011 -0.011 -0.010 -0.017 2.50E-05 6.40E-05 8.10E-05 1.44E-04 6.40E-05 1.00E-04 1.21E-04 1.21E-04 1.00E-04 2.89E-04 Sum ∑ 3.37·10-3 With = 50 and = 2 7.03·10-5 0.008
- 92. Experiment 7: Quantification of vitamin C 90 Metrohm Monograph 8.108.5020EN Calculation of the limit of quantification = 0.008 µA B = 0.038 µA·L·mg-1 Limit of detection (LOD) = 3· / B = 0.66 mg/L ≙ 0.028 µA Limit of quantification (LOQ) = 10· / B = 2.20 mg/L ≙ 0.087 µA Figure 46: Limit of detection and limit of quantification for the determination of vitamin C. 0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.0 2.0 4.0 6.0 8.0 10.0 I p / µA Concentration /mg·L-1 Measured values Linear regression LOD LOQ 3·sy 10·sy
- 93. Examples Electrochemistry – A workbook for 910 PSTAT mini 91 7.2.3 Determination of vitamin C in multivitamin products Sample Multivitamin effervescent tablet Vitamin C content: 60 mg/tablet Sample preparation 1 tablet dissolved in 200 mL ultrapure water. Measuring solution 10 mL ultrapure water 1 mL ammonium acetate buffer pH 4.6 0.5 mL sample solution Calibration curve Figure 47: Calibration curve for the determination of vitamin C. (Measuring solution: 10 mL H2O + 1 mL ammonium acetate buffer + ). Concentration standard: β(vitamin C) = 1 g/L / mL / mL β(vitamin C) / mg·L-1 * / µA 0.05 11.05 4.5 0.187 0.10 11.10 9.0 0.355 0.15 11.15 13.5 0.520 0.20 11.20 17.9 0.683 0.25 11.25 22.2 0.841 0.30 11.30 26.5 0.997 0.35 11.35 30.8 1.153 0.40 11.40 35.1 1.297 0.45 11.45 39.3 1.442 0.50 11.50 43.5 1.583 * Mean of 2 replications Linear regression: y = A + B·x Regression parameters: Intercept (A) / µA 0.036 Slope (B) / µA·L·mg-1 0.036 0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 0.0 20.0 40.0 I p / µA β(vitamin C) / mg·L-1
- 94. Experiment 7: Quantification of vitamin C 92 Metrohm Monograph 8.108.5020EN Sample with calibration curve Figure 48: Determination of vitamin C in multivitamin effervescent tablet with calibration curve. Vitamin C / µA / µA Replication 1 0.407 0.405 Replication 2 0.403 With regression parameters from calibration curve: Intercept (A) / µA 0.036 Slope (B) / µA·L·mg-1 0.036 β(Vitamin C) = 10.3 mg/L Volume correction: – Concentration in the measuring solution 10.3 mg/L – Total volume of the measuring solution 11.5 mL – Volume of sample in the measuring solution 0.5 mL – Concentration in the sample β(vitamin C) = 236.5 mg/L 1 tablet dissolved in 200 mL water w(vitamin C) = 47.3 mg/tablet 0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 0.0 10.0 20.0 30.0 40.0 I p / µA β(vitamin C) / mg·L-1
- 95. Examples Electrochemistry – A workbook for 910 PSTAT mini 93 Sample with standard addition Figure 49: Determination of vitamin C in multivitamin effervescent tablet with standard addition. Concentration standard: β(vitamin C) = 1 g/L Vitamin C / mL / mL β(vitamin C) / mg·L-1 / µA / µA Sample 0.0 11.5 0.0 0.407 0.403 0.405 1st addition 0.1 11.6 8.6 0.666 0.665 0.665 2nd addition 0.2 11.7 17.1 0.922 0.911 0.916 Linear regression: y = A + B x Intercept (A) / µA 0.406 Slope (B) / µA·L·mg-1 0.030 for y = 0 it is -x = A / B β(vitamin C) = 13.6 mg/L Volume correction: – Concentration in the measuring solution 13.6 mg/L – Total volume of the measuring solution 11.5 mL – Volume of sample in the measuring solution 0.5 mL – Concentration in the sample β(vitamin C) = 312.1 mg/L 1 tablet dissolved in 200 mL water w(vitamin C) = 62 mg/tablet 0.0 0.2 0.4 0.6 0.8 1.0 -15.0 -10.0 -5.0 0.0 5.0 10.0 15.0 20.0 Ip / µA β(vitamin C) / mg·L-1
- 96. Experiment 7: Quantification of vitamin C 94 Metrohm Monograph 8.108.5020EN Result discussion The specified amount of vitamin C in the effervescent tablet is 60 mg. With the calibration curve a content of 47.3 mg/tablet is determined, which corresponds to 78.8 % of the specified amount. With the standard addition technique a content of 62 mg/tablet is determined, which corresponds to 103.3 % of the specified amount. The result obtained with the standard addition technique is much closer to the specified amount of vitamin C in the tablet. The reasons are the compensation of matrix and electrode effects. These are two of the main advantages of the standard addition technique over the calibration curve. Therefore the standard addition technique would be the calibration technique of choice to determine vitamin C in multivitamin products. Advantages and disadvantages of the two calibration techniques are summarized below. Calibration curve technique Advantage Disadvantage Fast for large number of samples, since only one measurement in the sample is required once the calibration curve is established. New calibration curve required when a new electrode is used (not feasible when the electrode only lasts for a few measurements). Sometimes outdated calibration curves are not recognized. Matrix effects - Influence of the matrix on the result difficult to detect. - Incorrect results due to matrix effects. - Difficult to overcome matrix effects. Standard addition technique Advantage Disadvantage Calibration in each determination. Matrix effects minimized. Effects from differing sensitivity of different electrodes eliminated. Relatively slow, since at least one measurement in the sample plus the measurement of one addition are necessary. For reliable results the measurement of two additions is recommended.
- 97. Examples Electrochemistry – A workbook for 910 PSTAT mini 95 Experiment 8: Quantification of mercury 8.2.1 Initial preparation of the electrode Figure 50: Example for the change in the base line during the conditioning of the gold electrode. Displayed is the 1st , 10th and 20th replication (conditioning solution: 11 mL H2O + 0.1 mL HClO4). 8.2.2 Linear working range Concentration standard: β(Hg) = 10 mg/L / mL / mL β(Hg) / µg·L-1 * / µA 0.04 11.04 36.2 1.317 0.08 11.08 72.2 2.960 0.12 11.12 107.9 4.354 0.16 11.16 143.4 5.797 0.20 11.20 178.6 7.317 0.24 11.24 213.5 8.428 * Mean of 2 replications Concentrations outside the linear working range are marked gray. Figure 51: Linear working range for the determination of mercury. (Measuring solution: 10 mL ultrapure water + 1 mL supporting electrolyte + ). mean of 2 replications. 1st 10th 20th
- 98. Experiment 8: Quantification of mercury 96 Metrohm Monograph 8.108.5020EN Figure 52: Linear working range for the determination of mercury. 8.2.3 Limit of quantification Calibration curve for the determination of LOD and LOQ Figure 53: Example for curves recorded for the determination of LOD and LOQ for mercury. (Measuring solution: 10 mL H2O + 1 mL supporting electrolyte + ). 0 1 2 3 4 5 6 7 8 9 0.0 50.0 100.0 150.0 200.0 Ip / µA c(Hg) / µg·L-1 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 0.0 20.0 40.0 60.0 80.0 Ip /µA Concentration /µg·L-1 Linear working range Hg
- 99. Examples Electrochemistry – A workbook for 910 PSTAT mini 97 Concentration standard: β(Hg) = 10 mg/L Solution / mL / mL β(Hg) / µg·L-1 * / µA ̂ / µA Blank 0.000 11.000 0.0 0.047 -0.182 Standard 1 0.020 11.020 18.1 0.486 0.471 Standard 2 0.040 11.040 36.2 1.114 1.123 Standard 3 0.060 11.060 54.2 1.756 1.772 Standard 4 0.080 11.080 72.2 2.418 2.418 Standard 5 0.100 11.100 90.1 3.073 3.063 * Mean of 8 replications Linear regression: y = A + B·x Regression parameters: Intercept (A) -0.182 µA Slope (B) 0.036 µA·L·µg-1 Calculation of the residual standard deviation ∑ ( ̂ ) (Eq. 6) Solution β(Hg) / µg·L-1 / µA ̂ / µA ̂ ( ̂ ) Blank 0.0 0.031 0.139 0.040 0.041 0.025 0.031 0.040 0.026 -0.182 0.213 0.321 0.222 0.223 0.207 0.213 0.222 0.208 4.56E-02 1.03E-01 4.95E-02 4.99E-02 4.30E-02 4.56E-02 4.95E-02 4.35E-02 Standard 1 18.1 0.499 0.455 0.483 0.517 0.494 0.500 0.455 0.484 0.471 0.028 -0.016 0.012 0.046 0.023 0.029 -0.016 0.013 7.69E-04 2.64E-04 1.38E-04 2.09E-03 5.17E-04 8.26E-04 2.64E-04 1.62E-04 Standard 2 36.2 1.079 1.135 1.087 1.132 1.125 1.135 1.087 1.132 1.125 -0.044 0.012 -0.036 0.009 0.002 0.012 -0.036 0.009 1.92E-03 1.49E-04 1.28E-03 8.49E-05 4.91E-06 1.49E-04 1.28E-03 8.49E-05 Standard 3 54.2 1.725 1.743 1.760 1.756 1.796 1.725 1.743 1.796 1.774 -0.047 -0.029 -0.012 -0.016 0.024 -0.047 -0.029 0.024 2.18E-03 8.25E-04 1.37E-04 2.47E-04 5.90E-04 2.18E-03 8.25E-04 5.90E-04
- 100. Experiment 8: Quantification of mercury 98 Metrohm Monograph 8.108.5020EN Standard 4 72.2 2.347 2.355 2.424 2.468 2.579 2.347 2.355 2.468 2.420 -0.071 -0.063 0.006 0.050 0.161 -0.071 -0.063 0.050 5.09E-03 4.01E-03 3.24E-05 2.47E-03 2.58E-02 5.09E-03 4.01E-03 2.47E-03 Standard 5 90.1 3.024 2.985 3.079 3.151 3.086 3.024 3.151 3.086 3.064 -0.039 -0.078 0.016 0.088 0.023 -0.039 0.088 0.023 1.49E-03 6.02E-03 2.70E-04 7.82E-03 5.49E-04 1.49E-03 7.82E-03 5.49E-04 Sum ∑ 5.22·10-1 With = 40 and = 2 1.37·10-2 0.117 Calculation of the limit of quantification for mercury = 0.117 µA B = 0.036 µA·L·µg-1 Limit of detection (LOD) = 3· / B = 8.1 µg/L ≙ 0.108 µA Limit of quantification (LOQ) = 10· / B = 26.9 µg/L ≙ 0.786 µA Figure 54: Limit of detection and limit of quantification for the determination of mercury. -0.5 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 0.0 10.0 20.0 30.0 40.0 50.0 60.0 70.0 80.0 90.0 I p / µA Concentration /µg·L-1 Measured values Linear regression LOD LOQ 3·sy 10·sy
- 101. Examples Electrochemistry – A workbook for 910 PSTAT mini 99 8.2.4 Determination of mercury in air Sample Polluted air Since no contamination with mercury could be detected in ambient and workplace air the following setup was chosen to simulate polluted air. Approx. 100 g of mercury were filled into a 500 mL sample container. The container was closed tightly and kept at room temperature to allow the evaporation of mercury. After 1 day the air from the sample container was sampled with the described setup. Sample preparation Sampling: Shortly before the sampling the flame-sealed ends of the sorbent tube were broken off using a glass cutter. The sorbent tube was connected to the air pump as shown in Figure 55 and the air was sampled with the following conditions: Air flow 120 L/h Sampling time 60 min After the sampling time the sorbent tube was disconnected from the sampling unit and both ends were closed with the included sealing caps. Figure 55: Schematic setup for the sampling of mercury in air. Extraction: After removing the glass wool from the sorbent tube, the sorbent was completely transferred into a 10 mL volumetric flask. 2 mL w(HNO3) = 65 % were added and thoroughly mixed with the sorbent. Then 2 mL w(HCl) = 30 % were carefully added. Attention, vigorous reaction with intensive gas formation! After the reaction the volumetric flask was firmly closed and placed for 1 hour in a water bath at 50 °C. When cooled down to room temperature the test solution was made up to the mark with ultrapure water. Measuring solution 10 mL H2O 1 mL supporting electrolyte 0.5 mL test solution flow meter sorbent tube air pump connecting tube air flow glass wool sorbent
- 102. Experiment 8: Quantification of mercury 100 Metrohm Monograph 8.108.5020EN Calibration curve Figure 56: Calibration curve for the determination of mercury. (Measuring solution 10 mL H2O + 1 mL supporting electrolyte + ) Concentration standard: β(Hg) = 10 mg/L / mL / mL β(Hg) / µg·L-1 * / µA 0.040 11.040 36.2 1.317 0.060 11.060 54.2 2.076 0.080 11.080 72.2 2.960 0.100 11.100 90.1 3.649 0.120 11.120 107.9 4.354 0.140 11.140 125.7 5.023 0.160 11.160 143.4 5.797 0.180 11.180 161.0 6.585 0.200 11.200 178.6 7.317 * Mean of 2 replications Linear regression: y = A + B·x Regression parameters: Intercept (A) / µA -0.156 Slope (B) / µA·L·µg-1 0.042 0.0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 0.0 50.0 100.0 150.0 200.0 I p / µA β(Hg)/ µg·L-1
- 103. Examples Electrochemistry – A workbook for 910 PSTAT mini 101 Sample with calibration curve Figure 57: Determination of mercury air with calibration curve. Hg / µA / µA Replication 1 2.057 2.083 Replication 2 2.108 With regression parameters from calibration curve: Intercept (A) / µA -0.156 Slope (B) / µA·L·mg-1 0.042 β(Hg) = 53.6 µg/L Volume correction: – Concentration in the measuring solution 53.6 µg/L – Total volume of the measuring solution 11.5 mL – Volume of test solution in the measuring solution 0.5 mL – Concentration in the test solution β(Hg) = 1.23 mg/L With Concentration of mercury in the test solution β(Hg) = 1.23 mg/L Total volume of test solution 10 mL = 0.01 L Gas flow 120 L/h = 0.12 m3 /h Sampling time 1 h βair(Hg) = 0.10 mg/m3 0.0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 0.0 50.0 100.0 150.0 200.0 Ip / µA β(Hg) / µg·L-1
- 104. Experiment 8: Quantification of mercury 102 Metrohm Monograph 8.108.5020EN Assuming the mercury in the test tube is only deriving from the mercury vapor in the sample container, the concentration of mercury in the air space of the sample container is: Concentration of mercury in the test solution β(Hg) = 1.23 mg/L Total volume of test solution 10 mL = 0.01 L Total volume of the sample container 620 mL = 0.62·10-3 m3 βair(Hg) = 19.84 mg/m3 Sample with standard addition Figure 58: Determination of mercury in air with standard addition. Concentration standard: β(Hg) = 10 mg/L Hg / mL / mL β(Cd) / µg·L-1 / µA / µA Sample 0.000 11.500 0.0 2.057 2.108 2.083 1st addition 0.025 11.525 21.7 2.946 3.058 3.002 2nd addition 0.050 11.550 43.3 3.993 3.995 3.994 Linear regression: y = A + B x Intercept (A) / µA 2.070 Slope (B) / µA·L·µg-1 0.044 for y = 0 it is -x = A / B β(Hg) = 46.9 µg/L 0.0 1.0 2.0 3.0 4.0 5.0 -50.0 -30.0 -10.0 10.0 30.0 50.0 Ip / µA β(Hg)/ µg·L-1
- 105. Examples Electrochemistry – A workbook for 910 PSTAT mini 103 Volume correction: – Concentration in the measuring solution 46.9 µg/L – Total volume of the measuring solution 11.5 mL – Volume of sample in the measuring solution 0.5 mL – Concentration in the test solution β(Hg) = 1.08 mg/L With Concentration of mercury in the test solution β(Hg) = 1.08 mg/L Total volume of test solution 10 mL = 0.01 L Gas flow 120 L/h = 0.12 m3 /h Sampling time 1 h βair(Hg) = 0.09 mg/m3 Assuming the mercury in the test tube is only deriving from the mercury vapor in the sample container, the concentration of mercury in the air space of the sample container is: Concentration of mercury in the test solution β(Hg) = 1.08 mg/L Total volume of test solution 10 mL = 0.01 L Total volume of the sample container 620 mL = 0.62·10-3 m3 βair(Hg) = 17.42 mg/m3 Result discussion Referring to the air volume which was sampled in 1 hour, the concentration of mercury found with the calibration curve technique was 0.10 mg/m3 and with the standard addition curve 0.09 mg/m3 . The fact that the two results are quite similar indicates that there is no significant interference from the sample matrix. Therefore both calibration techniques can be used for this application. Nevertheless standard addition should be preferred because of the advantages and disadvantages summarized below. A quite interesting result is obtained if the result is not calculated with respect to the total volume of air sampled in 1 hour but only with respect to the available air space in the sample container which would represent the concentration of mercury vapor in the closed sample container. The concentration was found to be βair(Hg) = 19.84 mg/m3 by calibration curve and βair(Hg) = 17.42 mg/m3 by standard addition. These values are in a good agreement with the mass concentration of mercury in air at equilibrium that can be found in the literature (21) : β(Hg) = 13.6 mg/m3 at 20 °C β(Hg) = 29.6 mg/m3 at 30 °C
- 106. Experiment 8: Quantification of mercury 104 Metrohm Monograph 8.108.5020EN Calibration curve technique Advantage Disadvantage Fast for large number of samples, since only one measurement in the sample is required once the calibration curve is established. New calibration curve required when a new electrode is used (not feasible when the electrode only lasts for a few measurements). Sometimes outdated calibration curves are not recognized. Matrix effects - Influence of the matrix on the result difficult to detect. - Incorrect results due to matrix effects. - Difficult to overcome matrix effects. Standard addition technique Advantage Disadvantage Calibration in each determination. Matrix effects minimized. Effects from differing sensitivity of different electrodes eliminated. Relatively slow, since at least one measurement in the sample plus the measurement of one addition are necessary. For reliable results the measurement of two additions is recommended.
- 107. Examples Electrochemistry – A workbook for 910 PSTAT mini 105 Experiment 9: Quantification of cadmium and lead 9.2.1 Preparation of the mercury film Figure 59: Example for the potential scan after the plating of the mercury film (measuring solution: 12 mL Hg plating solution), signal at -0.6 V is due to lead impurities in the plating solution.
- 108. Experiment 9: Quantification of cadmium and lead 106 Metrohm Monograph 8.108.5020EN 9.2.2 Deposition potential Edep / V (Cd)* / µA (Pb)* / µA -0.5 0.940 0.817 -0.6 0.975 1.287 -0.7 0.912 4.677 -0.8 1.192 5.851 -0.9 7.905 6.324 -1.0 8.197 6.491 -1.2 8.426 6.299 -1.4 8.138 6.136 * Mean of 2 replications Figure 60: Example for the influence of the deposition potential on the peak height. (Measuring solution: 10 mL H2O + 1 mL buffer pH 4.4 + 0.1 mL Cd standard solution (β(Cd) = 10 mg/L) + 0.1 mL Pb standard solution (β(Pb) = 0.1 mg/L)). Figure 61: Pseudo-polarogram for cadmium and lead. Result discussion The so-called «pseudo-polarogram» shows the peak height of the stripping signal as a function of the deposition potential. At potentials more positive than the peak potential of the Me/Me2+ system (Cd/Cd2+ at approx. -0.8 V or Pb/Pb2+ at approx. -0.6 V) no deposition of metal can be observed. The peak height reaches the maximum at a deposition potential of approx. 200 mV more negative than the peak potential. Applying a more negative potential does not further increase the peak height. It can be concluded that -1.0 V or better yet -1.2 V would be suitable deposition potentials for the determination of cadmium and lead at the mercury film electrode. 0 2 4 6 8 10 -1.5 -1.3 -1.1 -0.9 -0.7 -0.5 Ip / µA Edep / V Cd Pb
- 109. Examples Electrochemistry – A workbook for 910 PSTAT mini 107 9.2.3 Linear working range Cadmium Concentration standard: β(Cd) = 10 mg/L / mL / mL β(Cd) / µg·L-1 * / µA 0.050 11.100 45.0 4.934 0.100 11.200 89.3 9.880 0.150 11.300 132.7 14.756 0.200 11.400 175.4 18.724 0.250 11.500 217.4 22.662 0.300 11.600 258.6 26.026 0.350 11.700 299.1 28.100 0.400 11.800 339.0 29.243 * Mean of 2 replications Concentrations outside the linear working range are marked gray. Figure 62: Linear working range for the determination of cadmium. (Measuring solution 10 mL H2O + 1 mL buffer pH 4.4 + ). Figure 63: Linear working range for the determination of cadmium. 0 5 10 15 20 25 30 0 50 100 150 200 250 300 350 Ip / µA c(Cd) / µg·L-1 Linear working range Cd
- 110. Experiment 9: Quantification of cadmium and lead 108 Metrohm Monograph 8.108.5020EN Lead Concentration standard: β(Pb) = 10 mg/L / mL / mL β(Pb) / µg·L-1 * / µA 0.050 11.100 45.0 3.024 0.100 11.200 89.3 6.094 0.150 11.300 132.7 9.317 0.200 11.400 175.4 12.041 0.250 11.500 217.4 15.186 0.300 11.600 258.6 18.106 0.350 11.700 299.1 19.887 0.400 11.800 339.0 21.228 * Mean of 2 replications Concentrations outside the linear working range are marked gray. Figure 64: Linear working range for the determination of lead. (Measuring solution 10 mL H2O + 1 mL buffer pH 4.4 + ). Figure 65: Linear working range for the determination of lead. 0 5 10 15 20 25 0 50 100 150 200 250 300 350 Ip / µA c(Pb) / µg·L-1 Linear working range Pb
- 111. Examples Electrochemistry – A workbook for 910 PSTAT mini 109 9.2.4 Limit of quantification Cadmium Figure 66: Example for curves recorded for the determination of LOD and LOQ for cadmium and lead. (Measuring solution 10 mL H2O + 1 mL buffer pH 4.4 + ) Concentration standard: β(Cd) = 0.2 mg/L Solution / mL / mL β(Cd) / µg·L-1 * / µA ̂ / µA Blank 0.0 11.0 0.00 0.004 -0.017 Standard 1 0.1 11.1 1.80 0.147 0.157 Standard 2 0.2 11.2 3.57 0.333 0.327 Standard 3 0.3 11.3 5.31 0.506 0.494 Standard 4 0.4 11.4 7.02 0.658 0.659 Standard 5 0.5 11.5 8.70 0.813 0.820 * Mean of 10 replications Linear regression: y = A + B·x Regression parameters: Intercept (A) -0.017 µA Slope (B) 0.096 µA·L·µg-1 Calculation of the residual standard deviation ∑ ( ̂ ) (Eq. 6) 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0.0 2.0 4.0 6.0 8.0 Ip /µA Concentration /µg·L-1 Cd
- 112. Experiment 9: Quantification of cadmium and lead 110 Metrohm Monograph 8.108.5020EN Solution β(Cd) / µg·L-1 / µA ̂ / µA ̂ ( ̂ ) Blank 4.5 0.003 0.003 0.002 0.008 0.005 0.006 0.008 0.004 0.003 0.004 -0.017 0.020 0.020 0.019 0.025 0.022 0.023 0.025 0.021 0.020 0.021 3.81E-04 3.81E-04 3.43E-04 6.01E-04 4.63E-04 5.07E-04 6.01E-04 4.21E-04 3.81E-04 4.21E-04 Standard 1 9.0 0.138 0.147 0.149 0.146 0.153 0.148 0.152 0.145 0.152 0.146 0.157 -0.019 -0.010 -0.008 -0.011 -0.004 -0.009 -0.005 -0.012 -0.005 -0.011 3.56E-04 9.71E-05 6.17E-05 1.18E-04 1.49E-05 7.84E-05 2.36E-05 1.41E-04 2.36E-05 1.18E-04 Standard 2 13.5 0.329 0.333 0.335 0.340 0.329 0.336 0.337 0.311 0.330 0.339 0.327 0.002 0.006 0.008 0.013 0.002 0.009 0.010 -0.016 0.003 0.012 3.53E-06 3.46E-05 6.21E-05 1.66E-04 3.53E-06 7.88E-05 9.76E-05 2.60E-04 8.28E-06 1.41E-04 Standard 3 17.9 0.500 0.500 0.506 0.512 0.514 0.506 0.512 0.508 0.497 0.513 0.494 0.006 0.006 0.012 0.018 0.020 0.012 0.018 0.014 0.003 0.019 3.16E-05 3.16E-05 1.35E-04 3.11E-04 3.85E-04 1.35E-04 3.11E-04 1.86E-04 6.89E-06 3.47E-04 Standard 4 22.2 0.646 0.660 0.661 0.663 0.660 0.662 0.651 0.663 0.658 0.649 0.659 -0.013 0.001 0.002 0.004 0.001 0.003 -0.008 0.004 -0.001 -0.010 1.61E-04 1.71E-06 5.32E-06 1.85E-05 1.71E-06 1.09E-05 5.92E-05 1.85E-05 4.81E-07 9.40E-05 Standard 5 26.5 0.810 0.815 0.817 0.815 0.808 0.805 0.816 0.806 0.804 0.796 0.820 -0.010 -0.005 -0.003 -0.005 -0.012 -0.015 -0.004 -0.014 -0.016 -0.024 1.03E-04 2.66E-05 9.95E-06 2.66E-05 1.48E-04 2.30E-04 1.73E-05 2.00E-04 2.61E-04 5.83E-04 Sum ∑ 1.02·10-2 With = 50 and = 2 2.13·10-4 0.015
- 113. Examples Electrochemistry – A workbook for 910 PSTAT mini 111 Calculation of the limit of quantification for cadmium = 0.015 µA B = 0.096 µA·L·µg-1 Limit of detection (LOD) = 3· / B = 0.46 µg/L ≙ 0.028 µA Limit of quantification (LOQ) = 10· / B = 1.52 µg/L ≙ 0.131 µA Figure 67: Limit of detection and limit of quantification for the determination of cadmium. Lead Figure 68: Example for curves recorded for the determination of LOD and LOQ for cadmium and lead. (Measuring solution 10 mL H2O + 1 mL buffer pH 4.4 + ) -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0.0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0 I p / µA Concentration /µg·L-1 Measured values Linear regression LOD LOQ 3·sy 10·sy 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0.0 2.0 4.0 6.0 8.0 10.0 12.0 Ip / µA Concentration /µg·L-1 Pb
- 114. Experiment 9: Quantification of cadmium and lead 112 Metrohm Monograph 8.108.5020EN Concentration standard: β(Pb) = 0.3 mg/L Solution / mL / mL β(Pb) / µg·L-1 * / µA ̂ / µA Blank 0.0 11.0 0.00 0.010 0.005 Standard 1 0.1 11.1 2.70 0.171 0.186 Standard 2 0.2 11.2 5.36 0.372 0.364 Standard 3 0.3 11.3 7.96 0.554 0.539 Standard 4 0.4 11.4 10.53 0.714 0.710 Standard 5 0.5 11.5 13.04 0.866 0.879 * Mean of 10 replications Linear regression: y = A + B·x Regression parameters: Intercept (A) 0.005 µA Slope (B) 0.067 µA·L·µg-1 Calculation of the residual standard deviation ∑ ( ̂ ) (Eq. 6) Solution β(Pb) / µg·L-1 / µA ̂ / µA ̂ ( ̂ ) Blank 0.00 0.018 0.005 0.016 0.009 0.004 0.003 0.003 0.004 0.006 0.003 0.005 0.013 0.000 0.011 0.004 -0.001 -0.002 -0.002 -0.001 0.001 -0.002 1.76E-04 7.49E-08 1.27E-04 1.83E-05 5.28E-07 2.98E-06 2.98E-06 5.28E-07 1.62E-06 2.98E-06 Standard 1 2.70 0.164 0.176 0.165 0.172 0.177 0.174 0.178 0.184 0.176 0.185 0.186 -0.022 -0.010 -0.021 -0.014 -0.009 -0.012 -0.008 -0.002 -0.010 -0.001 4.78E-04 9.72E-05 4.35E-04 1.92E-04 7.85E-05 1.41E-04 6.18E-05 3.46E-06 9.72E-05 7.38E-07 Standard 2 5.36 0.391 0.359 0.366 0.375 0.371 0.364 0.374 0.369 0.340 0.376 0.364 0.027 -0.005 0.002 0.011 0.007 0.000 0.010 0.005 -0.024 0.012 7.42E-04 2.26E-05 5.03E-06 1.26E-04 5.25E-05 5.91E-08 1.05E-04 2.75E-05 5.64E-04 1.50E-04 Standard 3 7.96 0.569 0.554 0.548 0.547 0.552 0.553 0.548 0.546 0.539 0.030 0.015 0.009 0.008 0.013 0.014 0.009 0.008 9.30E-04 2.40E-04 9.01E-05 7.21E-05 1.82E-04 2.10E-04 9.01E-05 5.92E-05
- 115. Examples Electrochemistry – A workbook for 910 PSTAT mini 113 0.537 0.545 -0.002 0.006 2.27E-06 4.22E-05 Standard 4 10.53 0.734 0.713 0.708 0.720 0.697 0.699 0.685 0.707 0.682 0.685 0.710 0.024 0.003 -0.002 0.010 -0.013 -0.011 -0.025 -0.003 -0.028 -0.025 5.67E-04 7.90E-06 4.80E-06 9.62E-05 1.74E-04 1.25E-04 6.35E-04 1.02E-05 7.95E-04 6.35E-04 Standard 5 13.04 0.882 0.876 0.863 0.863 0.844 0.836 0.854 0.832 0.840 0.840 0.879 0.003 -0.003 -0.016 -0.016 -0.035 -0.043 -0.025 -0.047 -0.039 -0.039 9.69E-06 8.34E-06 2.52E-04 2.52E-04 1.22E-03 1.84E-03 6.19E-04 2.20E-03 1.51E-03 1.51E-03 Sum ∑ 1.81·10-2 With = 50 and = 2 3.77·10-4 0.019 Calculation of the limit of quantification for lead = 0.019 µA B = 0.067 µA·L·µg-1 Limit of detection (LOD) = 3· / B = 0.87 µg/L ≙ 0.063 µA Limit of quantification (LOQ) = 10· / B = 2.90 µg/L ≙ 0.199 µA Figure 69: Limit of detection and limit of quantification for the determination of lead. 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0.0 2.0 4.0 6.0 8.0 10.0 12.0 I p / µA Concentration/ µg·L-1 Measured values Linear regression LOD LOQ 3·sy 10·sy
- 116. Experiment 9: Quantification of cadmium and lead 114 Metrohm Monograph 8.108.5020EN 9.2.5 Determination of cadmium and lead in articles of daily use Sample Decanter made from lead glass Sample preparation The decanter was filled to the top with extraction solution (w(acetic acid) = 4 % v/v). After 24 hours at room temperature (approx. 23 °C) the complete extraction solution was transferred into a clean storage container. Measuring solution 10 mL H2O 1 mL buffer pH 4.4 1 mL extraction solution Cadmium Figure 70: Determination of cadmium in extraction solution from lead glass by standard addition. Concentration standard: β(Cd) = 0.5 mg/L Cd / mL / mL β(Cd) / µg·L-1 / µA / µA Sample 0.0 12.0 0 0.065 0.068 0.067 1st addition 0.1 12.1 4.1 0.471 0.466 0.469 2nd addition 0.2 12.2 8.1 0.891 0.898 0.895 Linear regression: y = A + B x Intercept (A) / µA 0.061 Slope (B) / µA·L·µg-1 0.101 for y = 0 it is -x = A / B β(Cd) = 0.6 µg/L 0.0 0.2 0.4 0.6 0.8 1.0 -1.0 1.0 3.0 5.0 7.0 9.0 Ip / µA β(Cd)/ µg·L-1 Cd
- 117. Examples Electrochemistry – A workbook for 910 PSTAT mini 115 Volume correction: – Concentration in the measuring solution 0.6 µg/L – Total volume of the measuring solution 12.0 mL – Volume of sample in the measuring solution 1 mL – Concentration in the sample β(Cd) = 7.2 µg/L Lead Figure 71: Determination of lead in extraction solution from lead glass by standard addition. Concentration standard: β(Pb) = 1 mg/L Pb / mL / mL β(Pb) / µg·L-1 / µA / µA Sample 0.0 12.0 0.0 0.602 0.591 0.597 1st addition 0.1 12.1 8.3 1.12 1.131 1.126 2nd addition 0.2 12.2 16.4 1.675 1.714 1.695 Linear regression: y = A + B x Intercept (A) / µA 0.588 Slope (B) / µA·L·µg-1 0.067 for y = 0 it is -x = A / B β(Pb) = 8.8 µg/L 0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 -10.0 -5.0 0.0 5.0 10.0 15.0 20.0 Ip / µA β(Pb) / µg·L-1 Pb
- 118. Experiment 9: Quantification of cadmium and lead 116 Metrohm Monograph 8.108.5020EN Volume correction: – Concentration in the measuring solution 8.8 µg/L – Total volume of the measuring solution 12.0 mL – Volume of sample in the measuring solution 1 mL – Concentration in the sample β(Pb) = 105.4 µg/L Result discussion The concentrations for cadmium and lead found in the extraction solution are β(Cd) = 7.2 µg/L and β(Pb) = 105.4 µg/L. These values are far below the tolerable limits e.g. in Germany β(Pb) = 4.0 mg/L and β(Cd) = 0.3 mg/L (as specified in EU directive 84/500/EEC(22) and adopted by German regulation BedGgstV(23) ). As far as the measured concentration of Cd is concerned, it has to be kept in mind that the concentration in the measuring solution is only β(Cd) = 0.6 µg/L which is below the limit of quantification of β(Cd) = 1.5 µg/L. Therefore a rather large error has to be expected for this result.
- 119. Examples Electrochemistry – A workbook for 910 PSTAT mini 117 Experiment 10: The principle of a glucose sensor 10.2.3 Linear working range β(glucose) / mg·L-1 * / µA * / µA·s 200 0.552 21.807 400 1.166 46.276 600 1.716 71.561 800 2.173 89.561 1000 2.527 106.075 * Mean of 5 injections Concentrations outside the linear working range are marked gray. Figure 72: Curves recorded to evaluate the linear working range for the determination of glucose on a GOx modified electrode. (Carrier solution: phosphate buffer pH 5.2). Figure 73: Linear working range for the determination of glucose on a GOx modified electrode. 0.0 20.0 40.0 60.0 80.0 100.0 0 200 400 600 800 1000 Ap / µA·s β(glucose) / mg·L-1 Linear working range
- 120. Experiment 10: The principle of a glucose sensor 118 Metrohm Monograph 8.108.5020EN 10.2.4 Interferences / µA / µA·s β(glucose) = 400 mg/L 1.051 38.128 β(vitamin C) = 10 mg/L 1.274 46.290 Figure 74: Interference of vitamin C in the determination of glucose on a GOx modified electrode. (Carrier solution: phosphate buffer pH 5.2). Result discussion No interference can be observed from other sugars. Even the disaccharide sucrose which contains one molecule of glucose does not show a signal in the measurement. However, at the potential of 0.5 V, which is used to oxidize the hydrogen peroxide, also vitamin C is oxidized. β(Vitamin C) = 10 mg/L would feign a concentration of approx. β(glucose) = 500 mg/L. Conversely this means, that the expected error of the glucose result will be less than 10 % if the concentration of vitamin C is not more than 0.2 % of the concentration of glucose. One possibility to overcome the interference of vitamin C could be the optimization of the oxidation potential. Depending on the electrolyte, the oxidation potential of vitamin C begins in the range of +0.2 V to +0.4 V (see experiments 5 and 7). The oxidation of hydrogen peroxide starts at around 0 V. Choosing a potential between 0 V and +0.2 V for the amperometric detection should allow the determination without the interference of vitamin C, but this hypothesis needs confirmation by experimental data. 10.2.5 Determination of glucose in different food products Sample Fruit juice: apple juice, grape juice Beverages: iced tea, cola soft drink Honey Sample solution juices and beverages 0.1 mL of the particular sample was pipetted into a 10 mL volumetric flask and made up to the mark with phosphate buffer. Honey stock solution 1.144 g honey was weight in, transferred into a 25 mL volumetric flask and dissolved and made up to the mark with phosphate buffer. Sample solution honey An aliquot of 0.1 mL honey stock solution was pipetted into a 10 mL volumetric flask and made up to the mark with phosphate buffer. β(glucose) = 400 mg/L β(vitamin C) = 10 mg/L
- 121. Examples Electrochemistry – A workbook for 910 PSTAT mini 119 Recovery test solution 1 0.1 mL honey stock solution and 0.075 mL of glucose stock solution (β(glucose) = 10 g/L) was pipetted into a 10 mL volumetric flask and made up to the mark with phosphate buffer. Recovery test solution 2 0.1 mL honey stock solution and 0.15 mL of glucose stock solution (β(glucose) = 10 g/L) was pipetted into a 10 mL volumetric flask and made up to the mark with phosphate buffer. Calibration curve Figure 75: Calibration curve for the determination of glucose on a GOx modified electrode. (Carrier solution: phosphate buffer pH 5.2). β(glucose) / mg·L-1 * / µA * / µA·s 50 0.132 4.783 100 0.255 9.173 200 0.513 18.745 300 0.751 27.619 400 0.986 36.586 500 1.199 44.897 600 1.380 52.719 * Mean of 3 injections Linear regression: y = A + B·x Regression parameters: Intercept (A) / µA·s 0.796 Slope (B) / µA·s·L·mg-1 0.088 0.0 10.0 20.0 30.0 40.0 50.0 0 200 400 600 A p / µA·s β(glucose) / mg·L-1
- 122. Experiment 10: The principle of a glucose sensor 120 Metrohm Monograph 8.108.5020EN Samples with calibration curve Apple juice made from concentrate Figure 76: Determination of glucose in apple juice with calibration curve (apple juice diluted 1:100 with phosphate buffer pH 5.2). Glucose / µA·s / µA·s Injection 1 16.230 16.250 Injection 2 15.980 Injection 3 16.540 With regression parameters from calibration curve: Intercept (A) / µA·s 0.796 Slope (B) / µA·s·L·mg-1 0.088 β(glucose) = 175.8 mg/L Volume correction: – Concentration in the sample solution 175.8 mg/L – Total volume of the sample solution 10 mL – Volume of sample in the sample solution 0.1 mL – Concentration in apple juice β(glucose) = 17.6 g/L 0.0 10.0 20.0 30.0 40.0 50.0 0 100 200 300 400 500 600 Ap / µA·s β(glucose) / mg·L-1
- 123. Examples Electrochemistry – A workbook for 910 PSTAT mini 121 Grape juice Figure 77: Determination of glucose in grape juice with calibration curve (grape juice diluted 1:100 with phosphate buffer pH 5.2). Glucose / µA·s / µA·s Injection 1 47.454 46.849 Injection 2 46.913 Injection 3 46.180 With regression parameters from calibration curve: Intercept (A) / µA·s 0.796 Slope (B) / µA·s·L·mg-1 0.088 β(glucose) = 524.0 mg/L Volume correction: – Concentration in the sample solution 524.0 mg/L – Total volume of the sample solution 10 mL – Volume of sample in the sample solution 0.1 mL – Concentration in grape juice β(glucose) = 52.4 g/L 0.0 10.0 20.0 30.0 40.0 50.0 0 100 200 300 400 500 600 Ap / µA·s β(glucose) / mg·L-1
- 124. Experiment 10: The principle of a glucose sensor 122 Metrohm Monograph 8.108.5020EN Iced tea Figure 78: Determination of glucose in iced tea with calibration curve (iced tea juice diluted 1:100 with phosphate buffer pH 5.2). Glucose / µA·s / µA·s Injection 1 27.824 28.413 Injection 2 28.669 Injection 3 28.747 With regression parameters from calibration curve: Intercept (A) / µA·s 0.796 Slope (B) / µA·s·L·mg-1 0.088 β(glucose) = 314.2 mg/L Volume correction: – Concentration in the sample solution 314.2 mg/L – Total volume of the sample solution 10 mL – Volume of sample in the sample solution 0.1 mL – Concentration in iced tea β(glucose) = 31.4 g/L 0.0 10.0 20.0 30.0 40.0 50.0 0 100 200 300 400 500 600 Ap / µA·s β(glucose) / mg·L-1
- 125. Examples Electrochemistry – A workbook for 910 PSTAT mini 123 Cola soft drink Figure 79: Determination of glucose in cola soft drink with calibration curve (cola soft drink diluted 1:100 with phosphate buffer pH 5.2). Glucose / µA·s / µA·s Injection 1 41.541 41.407 Injection 2 41.385 Injection 3 41.294 With regression parameters from calibration curve: Intercept (A) / µA·s 0.796 Slope (B) / µA·s·L·mg-1 0.088 β(glucose) = 462.1 mg/L Volume correction: – Concentration in the sample solution 462.1 mg/L – Total volume of the sample solution 10 mL – Volume of sample in the sample solution 0.1 mL – Concentration in cola soft drink β(glucose) = 46.2 g/L 0.0 10.0 20.0 30.0 40.0 50.0 0 100 200 300 400 500 600 Ap / µA·s β(glucose) / mg·L-1
- 126. Experiment 10: The principle of a glucose sensor 124 Metrohm Monograph 8.108.5020EN Honey Figure 80: Determination of glucose in honey with calibration curve (honey diluted with phosphate buffer pH 5.2). Glucose / µA·s / µA·s Injection 1 13.535 13.497 Injection 2 13.376 Injection 3 13.581 With regression parameters from calibration curve: Intercept (A) / µA·s 0.796 Slope (B) / µA·s·L·mg-1 0.088 β(glucose) = 144.5 mg/L Volume correction: – Concentration in the sample solution 144.5 mg/L – Total volume of the sample solution 10 mL – Volume of the aliquot of honey stock solution in the sample solution 0.1 mL – Concentration in honey stock solution β(glucose) = 14.5 g/L – Concentration in honey stock solution 14.5 mg/L – Total volume of the honey stock solution 25 mL – Amount of sample in the stock solution 1.144 g – Concentration in honey w(glucose) = 315.8 mg/g 0.0 10.0 20.0 30.0 40.0 50.0 0 100 200 300 400 500 600 Ap / µA·s β(glucose) / mg·L-1
- 127. Examples Electrochemistry – A workbook for 910 PSTAT mini 125 Recovery test solution Figure 81: Determination of glucose recovery in honey with calibration curve. Recovery test solution 1 Glucose / µA·s / µA·s Injection 1 21.236 20.305 Injection 2 19.835 Injection 3 19.845 With regression parameters from calibration curve: Intercept (A) / µA·s 0.796 Slope (B) / µA·s·L·mg-1 0.088 β(glucose) = 222.0 mg/L ( ) – concentration in the recovery test solution 222.0 mg/L – concentration in the sample solution 144.5 mg/L – spiked concentration 75 mg/L Recovery 103.3 % Recovery test solution 2 Glucose / µA·s / µA·s Injection 1 27.954 27.547 Injection 2 27.899 Injection 3 26.789 With regression parameters from calibration curve: Intercept (A) / µA·s 0.796 Slope (B) / µA·s·L·mg-1 0.088 β(glucose) = 304.4 mg/L 0.0 10.0 20.0 30.0 40.0 50.0 0 100 200 300 400 500 600 Ap / µA·s β(glucose) / mg·L-1 Recovery test solution 1 Recovery test solution 2
- 128. Experiment 10: The principle of a glucose sensor 126 Metrohm Monograph 8.108.5020EN ( ) – concentration in the recovery test solution 304.4 mg/L – concentration in the sample solution 144.5 mg/L – spiked concentration 150 mg/L Recovery 106.6 % Result discussion Recovery in honey = 75 mg/L 103.3 % = 150 mg/L 106.6 % The concentration of glucose in the honey sample solution was found to be β(glucose) = 144.5 mg/L. Spiking this solution with β(glucose) = 75 mg/L and β(glucose) = 150 mg/L respectively shows a recovery of 103.3 % and 106.6 %. This indicates that there is no significant interference from the matrix. Honey β(glucose) 315.8 mg/g Nutrition facts(24) Glucose: 22 – 41 % Vitamin C: 0.026 mg/g From the concentration in the honey sample solution a content of β(glucose) = 315.8 mg/g in honey can be calculated. A comparison with nutrition facts, which can be found in the literature, shows that the result of about 31 % glucose in honey is realistic. The expected vitamin C content does not affect the result for the glucose. Doing a rough calculation, considering the dilution of the honey for the measurement, the concentration of vitamin C in the sample solution was about 0.001 mg/L. This concentration is at least 100 times lower than the concentration of vitamin C that would trigger a signal in the measurement. Sample β(glucose) Sugar as specified on the bottle Apple juice 17.6 g/L 100 g/L Grape juice 52.4 g/L 160 g/L* Iced tea 31.4 g/L 80 g/L Cola soft drink 46.2 g/L 106 g/L The table to the left shows the comparison of the determined concentrations of glucose and the total amount of sugar specified on the bottles of the other samples. The fraction of glucose as part of the sugar represents between 18 % in apple juice to 44 % in cola soft drink. None of the samples contained vitamin C as an additive. * Carbohydrates, sugar not separately specified
- 129. Abbreviations Electrochemistry – A workbook for 910 PSTAT mini 127 12 Abbreviations SI unit Area of the working electrode cm2 Peak area µA·V or µA·s A Intercept of a linear regression AE Auxiliary electrode B Slope of a linear regression Concentration mol·L-1 Diffusion coefficient cm2 ·s-1 Diffusion coefficient of the reduced species, corresponds to the anodic signal cm2 ·s-1 Diffusion coefficient of the oxidized species, corresponds to the cathodic signal cm2 ·s-1 Peak potential V Peak potential of the anodic signal V Peak potential of the cathodic signal V Faraday constant (9.648·104 C·mol-1 ) Peak height µA Peak height of the anodic signal µA Peak height of the cathodic signal µA Standard rate constant for electron transfer cm·s-1 Number of electrons -- PEEK Polyether ether ketone PTFE Polytetrafluoro ethylene, most common name Teflon Molar gas constant (8.314 J·mol-1 ·K-1 ) RE Reference electrode Temperature K Volume L or cm3 w Mass concentration % or mg·g-1 WE Working electrode Charge transfer coefficient -- β Mass concentration g·L-1 or g·m-3 Scan rate V·s-1 𝜓 Charge transfer parameter --
- 131. Bibliography Electrochemistry – A workbook for 910 PSTAT mini 129 13 Bibliography 1. Metrohm Monograph. Introduction to Polarography and Voltammetry. Herisau : s.n., 2003. Order number 8.027.5003. 2. Monk, Paul M. S. Fundamentals of Electroynalytical Chemistry. Chichester : John Wiley & Sons, 2001. ISBN 0-471-88140-6. 3. Atkins, Peter W. Physikalische Chemie. Zweite Auflage. Weinheim : VCH Verlagsgesellschaft, 1996. ISBN 3-527-29275-6. 4. Hamann, Carl H., Hamnett, Andrew and Vielstich, Wolf. Electrochemistry. Weinheim : Wiley-VCH, 1998. ISBN 3-527-29096-6 (brosch.). 5. Bond, Alan M. Broadening Electrochemical Horizons. New York : Oxford University Press, 2002. ISBN 0-19-850478-0 (Hbk). 6. Bard, Allen J. and Faulkner, Larry R. Electrochemical Methods. New York : John Wiley & Sons, 1980. ISBN 0-471-05542-5. 7. Nicholson, Richard S. Theory and Application of Cyclic Voltammetry for Measurment of Electrode Reaction Kinetics. Analytical Chemistry. October 1965, Vol. 37, 11, pp. 1351-1355. 8. Sigma-Aldrich. Molecular Self-Assembly. Material Matters. 2006, Vol. 1, 2. 9. Thomas, F.G. and Henze, G. Introduction to Voltammetric Analysis - Theory and Practice. Collingwood VIC : CSIRO Publishing, 2001. ISBN 0-643-06593-8. 10. J. Mocak, A.M. Bond, S. Mitchell, G. Scollary. A statistical overview of standard (IUPAC and ACS) and new procedures for determining the limits of detection and quantification: Application to voltammetric and stripping techniques. Pure and Applied Chemistry. 69, 1997, Vol. 2, 297-328. 11. International Union of Pure and Applied Chemistry (IUPAC). Compendium of Analytical Nomenclature. (the "Orange book") 3rd Edition. Oxford : Blackwell Scientific Publications, 1997. 12. Metrohm. Application Bulletin 96/5: Determination of mercury at the rotating gold electrode by anodic stripping voltammetry. http://www.metrohm.com/com/Applications/literature2/Application_Bulletins.html. 13. ISO 17733:2004. Workplace air - Determination of mercury and inorganic mercury compounds. ISO - International Organization for Standardization. 2004. 14. Bundesanstalt für Arbeitsschutz und Arbeitsmedizin. TRGS 900 - Technische Regeln für Gefahrstoffe: Arbeitsplatzgrenzwerte (Technical Rules for Hazardous Substances: workplace exposure limits). 2006. http://www.baua.de. 15. United States Occupational Safty and Health Administration. Occupational Safety and Health Guideline for Mercury Vapor. http://www.osha.gov/SLTC/healthguidelines/mercuryvapor/recognition.html. 16. Metrohm. Application Bulletin 254/1: Determination of zinc, cadmium, lead and copper by anodic stripping voltammetry using carbon electrodes. http://www.metrohm.com/com/Applications/literature2/Application_Bulletins.html. 17. ISO 7086-1:2000. Glass hollowware in contact with food – Release of lead and cadmium – part 1: Test method. ISO - International Organization for Standardization. 2000. 18. ISO 7086-2:2000. Glass hollowware in contact with food – Release of lead and cadmium – part 2: Permissible limits. ISO - International Organization for Standardization. 2000. 19. Updike, S.J. and Hicks, G.P. The enzyme electrode, a miniature chemical transducer using immobilized enzyme activity. Nature. 214, 1967, pp. 986-988. 20. Wikipedia. Standard electrode potential (data page). Wikipedia - The Free Encyclopedia. [Online] [Cited: February 18, 2011.] http://en.wikipedia.org/wiki/Table_of_standard_electrode_potentials. 21. Berufsgenossenschaft der chemischen Industrie. Merkblatt: Quecksilber und seine Verbindungen. Weinheim : Verlag Chemie, 1980.
- 132. Bibliography 130 Metrohm Monograph 8.108.5020EN 22. European Commission. 84/500/EEC. Council Directive of 15 October 1984 on the approximation of the laws of the Member States relating to ceramic articles intended to come into contact with foodstuffs. 1984. http://ec.europa.eu/food/food/chemicalsafety/foodcontact/legisl_list_en.htm. 23. Bundesgesetzblatt, Germany. Bedarfsgegenständeverordnung. s.l. : Bundesanzeiger Verlagsgesellschaft mbH, 2011. 24. Wikipedia. Honig. [Online] [Cited: March 2, 2011.] http://de.wikipedia.org/wiki/Honig. 25. Buchberger, Wolfgang. Elektrochemische Analysenverfahren. Heidelberg : Spektrum Akademischer Verlag, 1998. ISBN 3-8274-0135-6. 26. Noel, M. and Vasu, K.I. Cyclic Voltammetry and the Frontiers of Electrochemistry. London : Aspect Publications Ltd., 1990. ISBN 1-85529-025-1.











![Standard reduction potential
Electrochemistry – A workbook for 910 PSTAT mini 9
2 Standard reduction potential
Reduction potential of different metals
The reduction potential is a measure for the affinity of a chemical substance to accept electrons.
Under given conditions it is specific for the element or substance. In this experiment the reduction
behavior of different metal ions will be tested and compared. The determination is carried out by
linear sweep voltammetry (LSV). For further reading on LSV see e.g. Metrohm Monograph,
Introduction to Polarography and Voltammetry(1)
or Monk, Electroanalytical Chemistry(2)
. For
further reading on the reduction potential see e.g. P.W. Atkins, Physical Chemistry(3)
or Hamann and
Vielstich, Electrochemistry(4)
.
2.1 Accessories and reagents
2.1.1 Accessories
910 PSTAT mini
Electrode cable 6.2163.000
Carbon electrode 6.1208.110 (WE – C, AE – C, RE – Ag)
Measuring vessel, measuring vessel cover and measuring vessel holder
Additional accessories (not included in the scope of delivery of the 910 PSTAT mini)
Magnetic stirrer with stirrer bar (e.g. Metrohm 728 Stirrer)
Pipettes
Volumetric flasks
2.1.2 Reagents
Potassium chloride solution, c(KCl) = 3 mol/L, e.g. Metrohm 6.2308.020
Nitric acid, w(HNO3) = 65 %, for trace analysis*
, CAS 7697-37-2
Gold standard solution, β(Au) = 1 g/L, H[AuCl4] in 1 mol/L HCl
Mercury(II) nitrate monohydrate, Hg(NO3)2 · H2O, puriss. p.a., CAS 7783-34-8
Copper nitrate trihydrate, Cu(NO3)2 · 3 H2O, puriss. p.a., CAS 10031-43-3
Bismuth nitrate pentahydrate, Bi(NO3)3 · 5 H2O, puriss. p.a., CAS 10035-06-0
Lead nitrate, Pb(NO3)2, p.a., CAS 10099-74-8
Ultrapure water type 1 (electrical resistivity > 18.2 MΩ·cm, TOC < 10 ppb)
Ready-to-use solutions
Supporting electrolyte c(KCl) = 0.1 mol/L
c(HNO3) = 0.2 mol/L
Pipette 6.67 mL KCl solution (c(KCl) = 3 mol/L) into a 200 mL
volumetric flask. Add 2.856 mL nitric acid (w(HNO3) = 65%)
and make up to the mark with ultrapure water.
*
e.g. Merck suprapur®
, Sigma-Aldrich TraceSelect®
or equivalent](https://image.slidesharecdn.com/electrochemistry-230413133540-15c18536/85/Electrochemistry-Calculation-User-Guide-Book-Metrohm-11-320.jpg)


















![SAM – Self-assembled monolayers
28 Metrohm Monograph 8.108.5020EN
Volumetric flasks
Ultrasonic bath
Small sample containers with cap (inner diameter approx. 1.5 cm) to hold the electrode during
self-assembly (e.g. Metrohm sample tubes 15 mL (6.2747.000))
Tweezers
6.1.2 Reagents
2-Mercapto acetic acid, HSCH2COOH, CAS 68-11-1
3-Mercapto propionic acid, HSC2H4COOH, CAS 107-96-0
6-Mercapto hexanoic acid, HSC5H10COOH, CAS 17689-17-7
11-Mercapto undecanoic acid, HSC10H20COOH, CAS 71310-21-9
Ethanol, puriss. p.a., CAS 64-17-5
Potassium hexacyanoferrate(III), K3[Fe(CN)6], puriss. p.a., CAS 13746-66-2
Acetic acid, w(CH3COOH) = 100 %, for trace analysis*
, CAS 64-19-7
Ammonia solution, w(NH3) = 25 %, for trace analysis*
, CAS 1336-21-6
Ultrapure water type 1 (electrical resistivity > 18.2 MΩ·cm, TOC < 10 ppb)
Ready-to-use solutions
Ammonium acetate buffer
pH 4.6
c(CH3COOH) = 2 mol/L
c(NH3) = 1 mol/L
Fill approx. 300 mL ultrapure water into a 500 mL volumetric
flask. Carefully add 55.5 mL acetic acid (100 %) and 37 mL
NH3 (25 %). Make up to the mark with ultrapure water.
2-MAA stock solution c(MAA) = 0.1 mol/L
Dissolve 92 mg 2-mercapto acetic acid (equals 69.4 µL) in
10 mL ethanol. The solution is stable for at least a month if
stored in the freezer.
3-MPA stock solution c(MPA) = 0.1 mol/L
Dissolve 106 mg 3-mercapto propionic acid (equals 87 µL) in
10 mL ethanol. The solution is stable for at least a month if
stored in the freezer.
6-MHA stock solution c(MHA) = 0.1 mol/L
Dissolve 148 mg 6-mercapto hexanoic acid (equals 138.4 µL)
in 10 mL ethanol. The solution is stable for at least a month if
stored in the freezer.
11-MUA stock solution c(MUA) = 0.1 mol/L
Dissolve 218 mg 11-mercapto undecanoic acid in 10 mL
ethanol. The solution is stable for at least a month if stored in
the freezer.
Hexacyanoferrate(III) stock
solution
c([Fe(CN)6]3-
) = 0.1 mol/L
Dissolve 0.33 g potassium hexacyanoferrate(III) in 10 mL
ultrapure water. The solution should be prepared freshly at the
day of use.
*
e.g. Merck suprapur®
, Sigma-Aldrich TraceSelect®
or equivalent](https://image.slidesharecdn.com/electrochemistry-230413133540-15c18536/85/Electrochemistry-Calculation-User-Guide-Book-Metrohm-30-320.jpg)


![SAM – Self-assembled monolayers
Electrochemistry – A workbook for 910 PSTAT mini 31
6.2.2 Characterization of the monolayer by cyclic voltammetry
The thickness of a monolayer ranges from a few tenth of a nanometer to a few nanometers, a size
which cannot be seen visually. Therefore technical equipment is required to characterize the
monolayer. Usually sophisticated instruments, like scanning tunneling microscopes (STM) or atomic
force microscopes (AFM), are used. For studying the structure of monolayers these techniques are
essential, but sometimes a more simple approach will do. In a cyclic voltammetric measurement the
reaction [Fe(CN)6]3-
+ e-
⇌ [Fe(CN)6]4-
shows one distinct oxidation and one distinct reduction signal.
The presence of a coating at the electrode will have an influence on the measurement of these
signals. This effect can be used for an indirect characterization and comparison of electrodes with
different coatings.
Measuring solution
10 mL H2O
1 mL ammonium acetate buffer
0.1 mL hexacyanoferrate(III) stock solution
Voltammetric parameters
Figure 14: Parameters for testing the monolayer by
cyclic voltammetry (experiment 6.2).
Measurement
a) Prepare the measuring solution by pipetting 10 mL ultrapure water, 1 mL ammonium acetate
buffer pH 4.6 and 0.1 mL hexacyanoferrate(III) stock solution into the measuring vessel. Put a
stirrer bar into the measuring vessel and stir the solution well.
b) Use tweezers to take the electrode out of the 2-MAA coating solution.
c) Rinse the electrode thoroughly with ultrapure water and assemble it with the measuring
vessel cover. Take care not to touch the active electrode surface with bare fingers. Immerse
the electrode into the measuring solution and close the measuring vessel with the measuring
vessel cover.](https://image.slidesharecdn.com/electrochemistry-230413133540-15c18536/85/Electrochemistry-Calculation-User-Guide-Book-Metrohm-33-320.jpg)
![SAM – Self-assembled monolayers
32 Metrohm Monograph 8.108.5020EN
d) Use a soft tissue to thoroughly dry the electrical contacts of the electrode. Make sure that the
contacts are completely dry and free from contaminants before connecting the electrode
cable.
e) Record the cyclic voltammogram with the voltammetric parameters given Figure 14. Make
sure the stirrer is switched off during the measurement.
f) Repeat step b) to e) with electrodes coated with 3-MPA, 6-MHA and 11-MUA instead of 2-
MAA.
Evaluation
g) Evaluate peak height of the cathodic signal as described in 6.2.3.
h) Plot a graph of the peak height as a function of the number of C atoms in the spacer group in
the molecule. What can be observed?
6.2.3 Curve evaluation
In principle the reduction and the oxidation signal can be used for the characterization. But in the
described measuring solution the effect of the monolayer on this cathodic signal is usually more
pronounced. This signal is related to the reduction [Fe(CN)6]3-
+ e-
⟶ [Fe(CN)6]4-
. For the evaluation of
the peak height it is recommended to use the «Step measurement tool».
Figure 15: Example for the
evaluation of peak height in
experiment 6.2.](https://image.slidesharecdn.com/electrochemistry-230413133540-15c18536/85/Electrochemistry-Calculation-User-Guide-Book-Metrohm-34-320.jpg)











































![Experiment 2: Standard reduction potential
76 Metrohm Monograph 8.108.5020EN
Hg Eobs = -0.01 V E0 = +0.85 V
Hg2+
(aq) + 2 e-
⇌ Hg(l)
Au Eobs = +0.33 V E0 = +0.93 V
[AuCl4]-
(aq) + 3 e-
⇌ Au(s) + 4 Cl-
Figure 32: Linear sweep voltammograms of different metal ions (gray line – supporting electrolyte, black line –
c(metal) = 0.18 mmol/L in the supporting electrolyte). Eobs – observed reduction potential, E0 – standard
reduction potential
(20)
.
Result discussion
When the metals are sorted by their reduction potential it can be seen that precious metals like gold
have the more positive potential, means they can more easily be reduced to their metallic form. Base
metals like lead have a more negative potential and can therefore more easily be oxidized to their
ionic form.
Base metal Precious metal
Negative reduction potential Positive reduction potential
Figure 33: Lead, copper, bismuth, mercury and gold sorted by their reduction potentials.
Pb2+
-0.68 V
Cu2+
-0.41 V
Bi3+
-0.28 V
Hg2+
-0.01 V
Au3+
+0.33 V +
–](https://image.slidesharecdn.com/electrochemistry-230413133540-15c18536/85/Electrochemistry-Calculation-User-Guide-Book-Metrohm-78-320.jpg)















































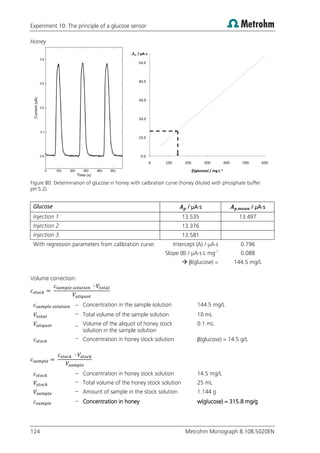




![Bibliography
Electrochemistry – A workbook for 910 PSTAT mini 129
13 Bibliography
1. Metrohm Monograph. Introduction to Polarography and Voltammetry. Herisau : s.n., 2003.
Order number 8.027.5003.
2. Monk, Paul M. S. Fundamentals of Electroynalytical Chemistry. Chichester : John Wiley & Sons,
2001. ISBN 0-471-88140-6.
3. Atkins, Peter W. Physikalische Chemie. Zweite Auflage. Weinheim : VCH Verlagsgesellschaft, 1996.
ISBN 3-527-29275-6.
4. Hamann, Carl H., Hamnett, Andrew and Vielstich, Wolf. Electrochemistry. Weinheim : Wiley-VCH,
1998. ISBN 3-527-29096-6 (brosch.).
5. Bond, Alan M. Broadening Electrochemical Horizons. New York : Oxford University Press, 2002.
ISBN 0-19-850478-0 (Hbk).
6. Bard, Allen J. and Faulkner, Larry R. Electrochemical Methods. New York : John Wiley & Sons,
1980. ISBN 0-471-05542-5.
7. Nicholson, Richard S. Theory and Application of Cyclic Voltammetry for Measurment of Electrode
Reaction Kinetics. Analytical Chemistry. October 1965, Vol. 37, 11, pp. 1351-1355.
8. Sigma-Aldrich. Molecular Self-Assembly. Material Matters. 2006, Vol. 1, 2.
9. Thomas, F.G. and Henze, G. Introduction to Voltammetric Analysis - Theory and Practice.
Collingwood VIC : CSIRO Publishing, 2001. ISBN 0-643-06593-8.
10. J. Mocak, A.M. Bond, S. Mitchell, G. Scollary. A statistical overview of standard (IUPAC and ACS)
and new procedures for determining the limits of detection and quantification: Application to
voltammetric and stripping techniques. Pure and Applied Chemistry. 69, 1997, Vol. 2, 297-328.
11. International Union of Pure and Applied Chemistry (IUPAC). Compendium of Analytical
Nomenclature. (the "Orange book") 3rd Edition. Oxford : Blackwell Scientific Publications, 1997.
12. Metrohm. Application Bulletin 96/5: Determination of mercury at the rotating gold electrode by
anodic stripping voltammetry.
http://www.metrohm.com/com/Applications/literature2/Application_Bulletins.html.
13. ISO 17733:2004. Workplace air - Determination of mercury and inorganic mercury compounds.
ISO - International Organization for Standardization. 2004.
14. Bundesanstalt für Arbeitsschutz und Arbeitsmedizin. TRGS 900 - Technische Regeln für
Gefahrstoffe: Arbeitsplatzgrenzwerte (Technical Rules for Hazardous Substances: workplace
exposure limits). 2006. http://www.baua.de.
15. United States Occupational Safty and Health Administration. Occupational Safety and Health
Guideline for Mercury Vapor.
http://www.osha.gov/SLTC/healthguidelines/mercuryvapor/recognition.html.
16. Metrohm. Application Bulletin 254/1: Determination of zinc, cadmium, lead and copper by
anodic stripping voltammetry using carbon electrodes.
http://www.metrohm.com/com/Applications/literature2/Application_Bulletins.html.
17. ISO 7086-1:2000. Glass hollowware in contact with food – Release of lead and cadmium – part
1: Test method. ISO - International Organization for Standardization. 2000.
18. ISO 7086-2:2000. Glass hollowware in contact with food – Release of lead and cadmium – part
2: Permissible limits. ISO - International Organization for Standardization. 2000.
19. Updike, S.J. and Hicks, G.P. The enzyme electrode, a miniature chemical transducer using
immobilized enzyme activity. Nature. 214, 1967, pp. 986-988.
20. Wikipedia. Standard electrode potential (data page). Wikipedia - The Free Encyclopedia. [Online]
[Cited: February 18, 2011.] http://en.wikipedia.org/wiki/Table_of_standard_electrode_potentials.
21. Berufsgenossenschaft der chemischen Industrie. Merkblatt: Quecksilber und seine Verbindungen.
Weinheim : Verlag Chemie, 1980.](https://image.slidesharecdn.com/electrochemistry-230413133540-15c18536/85/Electrochemistry-Calculation-User-Guide-Book-Metrohm-131-320.jpg)
![Bibliography
130 Metrohm Monograph 8.108.5020EN
22. European Commission. 84/500/EEC. Council Directive of 15 October 1984 on the approximation
of the laws of the Member States relating to ceramic articles intended to come into contact with
foodstuffs. 1984. http://ec.europa.eu/food/food/chemicalsafety/foodcontact/legisl_list_en.htm.
23. Bundesgesetzblatt, Germany. Bedarfsgegenständeverordnung. s.l. : Bundesanzeiger
Verlagsgesellschaft mbH, 2011.
24. Wikipedia. Honig. [Online] [Cited: March 2, 2011.] http://de.wikipedia.org/wiki/Honig.
25. Buchberger, Wolfgang. Elektrochemische Analysenverfahren. Heidelberg : Spektrum
Akademischer Verlag, 1998. ISBN 3-8274-0135-6.
26. Noel, M. and Vasu, K.I. Cyclic Voltammetry and the Frontiers of Electrochemistry. London :
Aspect Publications Ltd., 1990. ISBN 1-85529-025-1.](https://image.slidesharecdn.com/electrochemistry-230413133540-15c18536/85/Electrochemistry-Calculation-User-Guide-Book-Metrohm-132-320.jpg)