flow of fluids

FLUID FLOW
V.JAGAN MOHAN RAO M.S.Pharm., MED.CHEM
NIPER-KOLKATA
Asst.Professor, MIPER-KURNOOL
EMAIL- jaganvana6@gmail.com

FLUID FLOW
A fluid is a substance that continually deforms (flows) under an
applied shear stress. Fluids are a subset of the phases of matter and
include liquids, gases both.
Fluid flow may be defined as the flow of substances that do not
permanently resist distortion.
The subject of fluid flow can be divided into fluid statics and fluid
dynamics.
Identification of type of flow is important in
Manufacture of dosage forms
Handling of drugs for administration

FLUID STATICS
 Fluid statics deals with the fluids at rest in equilibrium,
 Behavior of liquid at rest
 Nature of pressure it exerts and the variation of pressure at
different layers
Pressure differences between layers of liquids
h1
h2
Point 1
Point 2

Consider a column of liquid with two openings Which are
provided atthe wall of the vessel at different height
The rate of flow through these opening s are different due tothe
pressure exerted at the differentheight
Consider a stationary column the pressure ps is acting on the surface of
the fluid, column is maintained at constant pressure by applyingpressure
The force acting below and above the point 1 areevaluated
Substituting the force with pressure x area of cross section in theabove
equation
Force acting on the liquid
At point 1 =
Force on the surface
+ Force excreted by theliquid
Above point 1
Pressure at point 1 x Area =
Pressure on the surface x area
+ mass x acceleration

P1S = PsS + volume x density x acceleration
= PsS + height x area x density x acceleration
P1S = PsS + h1 S ρ g
Since surface area is same
P1 = Ps + h1 ρ g
Pressure acting on point 2 may be written as
P2 = Ps + h2 ρ g
Difference in the pressure is obtained by
P2 - P1 = g (Ps + h2 ρ ) – ( Ps + h1 ρ) g
∆P = (Ps + h2 ρ– Ps - h1 ρ ) g
= ∆ h ρ g

FLUID DYNAMICS
 Fluid dynamics deals with the study of fluids in
motion
 This knowledge is important for liquids, gels,
ointments which will change their flowbehavior
when exposed to different stress conditions
MIXING
FLOW THROUGHPIPES
FILLED IN CONTAINER

 The flow of fluid through a
closed channel can be
viscous or turbulent and it can
be observed by;
 Reynolds experiment
 Consider Glass tube which is
connected to reservoir of
water, rate of flow of water is
adjusted by a valve, a
reservoir of colored solution is
connected to one end of the
glass tube with help of nozzle
colored solution is introduced
into the nozzle as fine stream.

Laminar flow is one in which the fluid particles move in
layersor laminar with one layer sliding with other.
There is no exchange of fluid particles from one layer to
other.
When velocity of the water is increased the thread of the
colored water disappears and mass of the water gets
uniformly colored, indicates complete mixing of the solution
and the flow of the fluid is called as turbulent flow.
The velocity at which the fluid changes from laminar flow
to turbulent flow that velocity is called as critical velocity.

REYNOLDS NUMBER
 Inertial forces are due to mass and the velocity of the fluidparticles
trying to diffuse the fluid particles
 viscous force if the frictional force due to the viscosity of thefluid
which make the motion of the fluid in parallel
In Reynolds experiment the flow conditions are affectedby
Diameter ofpipe
Average velocity
Density of liquid
Viscosity of the fluid
This four factors are combined in one way as Reynolds number
Reynolds number is obtained by the following equation
D u ρ
η
INERTIALFORCES
= ------------------------------ =
VISCOUS FORCES
MASS X ACCELERATION OF LIQUIDFLOWING
---------------------------------------------------------
SHEAR STRESS XAREA

 If Re < 2000 the flow is said to be laminar
 If Re > 4000 the flow is said to be turbulent
 If Re lies between 2000 to 4000 the flow change between
laminar to turbulent
 APPLICATIONS
 Reynolds number is used to predict the nature of theflow
 Stocks law equation is modified to include Reynolds number to study
the rate of sedimentation in suspension

BERNOULLI'S THEOREM
When the principals of the law of conservation energy is applied tothe
flow of the fluids the resulting equation is called Bernoulli's theorem
 Consider a pump working under isothermal conditions between pointsA
and B as shown in figure;

 At point a one kilogram of liquid is assumed to be entering atthis
point, pressure energy at joule can be writtenas
Pressure energy = Pa /g ρ A
Where Pa = Pressure at point a
g = Acceleration due togravity
ρ A = Density of theliquid
Potential energy of a body is defined as the energy possessedby
the body by the virtue of its position or configuration
Potential energy = XA
Kinetic energy of a body is defined as the energy possessed by the
body by virtue of its motion,
kinetic energy = UA / 2g2
Total energy at point A = Pressure energy + Potential energy+Kinetic
energy

Total energy at point A = Pa /g ρ A +XA + UA / 2g2
According to the Bernoulli's theorem the total energy atpoint
A is constant
Total energy at point A = Pa /g ρ A +XA + UA / 2g = Constant2
After the system reaches the steady state, whenever one kilogramof
liquid enters at point A, another one kilogram of liquid leaves at point B
Total energy at point B = PB /g ρ B +XB + UB / 2g2
INPOUT = OUT PUT
Pa /g ρ A +XA + U 2 / 2g =PB /g ρ B +XB + U 2 / 2g
A B
Theoretically all kids of the energies involved in fluid flow should be
accounted, pump has added certain amount ofenergy
Energy added by the pump = + wJ

• This equation is called as Bernoulli's
equation
• Application
 Used in the measurement of rate of fluidflow
 It applied in the working of the centrifugal pump, in this kinetic energyis
converted in to pressure
During the transport some energy is converted to heat due tofrictional Forces
Loss of energy due to friction in the line =FJ

ENERGY LOSS
 According to the law of conversation of energy ,energy balance
have to be properly calculated
 fluids experiences energy losses in several ways while
flowing through pipes, they are
 Frictional losses
 Losses in the fitting
 Enlargement losses
 Contraction losses

FRICTIONAL LOSSES
During flow of fluids frictional forces causes a loss in pressure Type of
fluid flow also influences the losses
In general pressure drop will be
PRESSURE DROP α VELOCITY (u)
α Density of fluid(ρ)
α Length of the pipe (L)
α 1 / diameter of the pipe (D)
These relationships are proposed in Fanning equation for calculating
friction losses
Fanning equation ∆p = 2fu2Lρ / D
F = frictional factor
For viscous flow pressure drop Hagen –Poiseullie equation
= 32 Luη / D2

LOSSES IN FITTING
Fanning equation is applicable for the losses in straight pipe When
fitting are introduced into a straight pipe, They cause disturbance in the
flow, Which result in the additional loss of energy
losses in fitting may be due to
Change in direction
Change in the type of fittings
Equivalent length of fitting = Equivalent length x internal diameter
For globe valve = 300 x 50
= 15 meter
That means globe valve is equal to 15 meters straight line, so this
length is substituted in fanning equation
Tee fitting
Equivalent length = 90
Globe valve equivalent length = 300

ENLARGEMENT LOSS
If the cross section of the pipe enlarges gradually, the fluid adaptsitself
to the changed section with out any disturbance So no loss of energy
If the cross section of the pipe changes suddenly then loss in energy is
observed due to eddies These are greater at this point than straight line
pipe
Than u2< u1
For sudden enlargement = ∆ H = (u1 –u2 )2 / 2g
∆ H = loss of head due to sudden enlargement
µ1 µ2
µ1
µ2

CONTRACTION LOSSES
If the cross section of the pipe is reduced suddenly the fluid flow is
disturbed, the diameter of the fluid stream is less than the initial value of
diameter this point of minimum cross section is known as vena
contracta.
the velocity of fluid at smaller cross section will be greater than at larger
cross section, u2> u1

MANOMETERS
Manometers are the devices used for measuring the pressure
difference Different type of manometers are;
1) Simple manometer
2) Differential manometer
3) Inclined manometer

SIMPLE MANOMETER
 This manometer is the most commonly used one
 It consists of a glass U shaped tube filled with a liquid A- of
density ρA kg /meter cube and above A the arms are filled with liquid B
of density ρB .
 The liquid A and B are immiscible and the interference can be seen
clearly
 If two different pressures are applied on the two arms the meniscusof
the one liquid will be higher than the other
 Let pressure at point 1 will be P1 Pascal's and point 5 will be P2
Pascal's
 The pressure at point 2 can be written as
= P1+ (m + R ) ρ B g
(m + R ) = distance from 3 to 5

P1 P2
m
R
1
2
3
4
5
LiquidA
LIQUIDB

Since the points 2 and 3 are at same height the pressure
at 3 can be written as
Pressure at 3 =P1+ (m + R ) ρ Bg
Pressure at 4 can be written as
= P2 + gm ρB
or
= P1+ ρ B ( m + R ) g- ρ a R g
Both the equations should be equal
P2 + gm ρ B = P1+ ρ B ( m + R ) g- ρ a R g
P1 – P2 = gm ρ B - ρ B ( m + R) g + ρ A R g
∆P = gm ρ B - gm ρ B - R ρ B g + R ρ A
=R (ρ A- ρ B )g

DIFFERENTIAL MANOMETERS
 These manometers are suitable for measurement of small
pressure differences
 It is also known as two – Fluid U- tube manometer
 It contains two immiscible liquids A and B having nearly same
densities
 The U tube contains of enlarged chambers on both limbs,
 Using the principle of simple manometer the pressure
differences canbe written as
∆P =P1 –P2 =R (ρc – ρA)g

INCLINED TUBE MANOMETERS
Many applications require accurate measurement of low
pressure suchas drafts and very low differentials, primarily in air
and gasinstallations
In these applications the manometer is arranged with the
indicatingtube inclined, as in Figure, therefore providing an
expanded scale
This enables the measurement of small pressure changes with
increased
accuracy
P1 –P2 = g R (ρ A - ρ B) sin α

MEASUREMENT OF RATE OF FLOW OF FLUIDS
When ever fluid are used in a process it is necessary to measurethe
rate at which the fluid is flowing through the pipe,
Methods of measurement are
Direct weighing or measuring
Hydrodynamic methods
Orifice meter
Venturi meter
Pitot meter
Rotameter
Direct displacement meter

The liquid flowing through a pipe is collected for specific period
at any point and weighed or measured, and the rate of flow canbe determined.
Gases can not be determined by thismethod.
ORIFICE METER
Principle:
Orifice meter is a thin plate containing a narrow and sharpaperture
When a fluid stream is allowed to pass through a narrow constrictionthe
velocity of the fluid increase compared to upstream
This results in decrease in pressure drop and the difference inthe
pressure may be read from amanometer
The velocity of the fluid at thin constriction may be writtenas
U0 =C 0 √ 2g∆H
DIRECT WEIGHING OR MEASURING

∆H = difference in height, can be measured by manometer C0
=constant
U0 = velocity of fluid at the point of orificemeter
CONSTRUCTION
 It is consider to be a thin plate containing a sharp aperturethrough
which fluid flows
 Normally it is placed between long straightpipes
 For present discussion plate is introduced into pipe and manometeris
connected at points A and B
WORKING
 Orifice meter is referred as the variable head meter, ie it measure the
variation in the pressure across a fixed construction placed in thepath
of flow

 When fluid is allowed to pass through the orifice the velocity of the fluid
at point B increase, as a result at point A pressure will be increased
 Difference in the pressure is measured by manometer
 Bernoulli's equation is applied to point A and point B for experimental
conditions
√µ0
2 –µ 2 =C √2g ∆H
A 0
µ0 = velocity of fluid atorifice
µA = velocity of fluid at point A
C0 = constant
 If the diameter of the orifice is 1/5 or less of the pipe diameter thenµA
µ0 = C0 √2g ∆His neglected so,
Applications
 Velocity at either of the point A and B can be measured
 Volume of liquid flowing per hour can be determined

VENTURI METER
• Principle:
 Venturi meter consist of two tapered sections in the
pipe line with a gradual constriction at its centre.
 When fluid stream is allowed to pass through the
narrow throat the velocity of the fluid increases at
the venturi compared to velocity of the upstream.
 This results in decrease in the pressure head.
 This resulting decrease in the pressure head is
measured directly from the manometer.

Disadvantages
 Expensive
 Need technical expert
 Not flexible
 Occupies more space
Advantages
 Power loss is less
 Head loss is negligible
Applications:
 It is commonly used for liquids, specially for water.
 It can also be used for the measurement of gases.

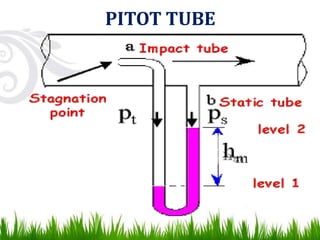
PITOT TUBE
• Principle:
 Pitot tube consists of sensing element with a small
constriction compared to the size of the flow
channel.
 When the sensing element is inserted at the center
of the stream, the velocity of flow is increased.
 This results in decrease in pressure head.
∆Hp = u2 /2g

Construction
 It is also known as insertion meter or insertion tube
 The size of the sensing element is small compared to theflow channel
 The point of measurement may be at the center of thechannel
 One tube is perpendicular to the flow direction and the otheris
parallel to the flow
 Two tubes are connected to themanometer
Working
 Tube are inserted in the flow shown is the figure.
 Pitot tube is used to measure the velocity head of the flow.
 In this tube velocity of fluid is increased at the narrow
constriction which results in decreased pressure.

 Tube at right angles to the flow measures
pressure head only while the tube that points
upstream measures pressure head and velocity
head.
µ2= Cv √2g ∆H
 Cv coefficient of Pitot tube

ROTAMETER
Principle:
 Rotameter is known as area meter as it measures area of
flow.
 It consist of a vertical, tapered and transparent tube in
which plummet is placed.
 During the fluid flow through the tube the plummet rises
and falls because of variation of flow.

Construction
 It consists of vertically tapered and transparent tube with narrow end
down, in which a plummet is placed.
 A solid plummet is placed in the tube. The diameter of the plummet is
smaller than the narrowest part of the tube.
 Floats/plummet is made up of glass, aluminium or plastic.
 The tube is usually made of glass on which linear scale is given.
 During the flow the plummet rise due to variation in flow
 The upper edge of the plummet is used as an index to note the reading

flow of fluids

More Related Content

What's hot (20)

Similar to flow of fluids (20)

More from jagan vana (20)

Recently uploaded (20)

flow of fluids