Functions & graphs

www.mathsrevision.com

Higher

Higher Unit 1
Outcome 2

What is a set
Recognising a Function in various formats
Composite Functions
Exponential and Log Graphs
Graph Transformations
Trig Graphs
Connection between Radians and degrees
Trig Exact Values
Basic Trig Identities
Exam Type Questions

Sets & Functions
Higher

Outcome 2


Notation & Terminology
SETS: A set is a collection of items which have
some common property.
These items are called the members or
elements of the set.
Sets can be described or listed using
“curly bracket” notation.

Sets & Functions
Outcome 2

Higher


eg

{colours in traffic lights}

DESCRIPTION

eg

{square nos. less than 30}

= {red, amber, green}

LIST

= { 0, 1, 4, 9, 16,
25}

NB: Each of the above sets is finite because we
can list every member

= {1, 2, 3, 4, ……….}
Sets & Functions
Outcome 2

Higher


We can describe numbers by the following sets:
N = {natural numbers}
W = {whole numbers} = {0, 1, 2, 3, ………..}
Z = {integers}
= {….-2, -1, 0, 1, 2, …..}
Q = {rational numbers}
This is the set of all numbers which can be written
as fractions or ratios.
eg

5 = 5/1

-7 =

-7

55

/1

0.6 = 6/10 = 3/5
11


Higher

Sets & Functions
Outcome 2

R = {real numbers}
This is all possible numbers. If we plotted values
on a number line then each of the previous sets
would leave gaps but the set of real numbers would
give us a solid line.
We should also note that
N

“fits inside”

W

W “fits inside”

Z

Z

Q

Q

“fits inside”
“fits inside”

R

Sets & Functions
Outcome 2

Higher


N

W

Z

Q

R

When one set can fit inside another we say
that it is a subset of the other.
The members of R which are not inside Q are called
irrational numbers. These cannot be expressed as
fractions and include π , √2, 3√5 etc

Sets & Functions
Outcome 2


Higher

To show that a particular element/number
belongs to a particular set we use the symbol ∈.
eg
3 ∈ W but
0.9 ∉ Z
Examples
{ x ∈ W: x < 5 } =
{ x ∈ Z: x ≥ -6 }
{ x ∈ R: x2 = -4 }

=

{ 0, 1, 2, 3, 4 }

{ -6, -5, -4, -3, -2,
…….. }
=
{ } or Φ

This set has no elements and is called the empty set.

Functions & Mappings

Higher

Outcome 2

Defn: A function or mapping is a relationship between
two sets in which each member of the first set
is connected to exactly one member in the second set.
If the first set is A and the second B then we often write

f: A → B
The members of set A are usually referred to as the
domain of the function (basically the starting values or
even x-values) while the corresponding values or images
come from set B and are called the range of the function
(these are like y-values).

Functions & Mapping
Outcome 2

Higher


Functions can be illustrated in three ways:
1) by a formula.
2) by arrow diagram.
3) by a graph

Example
FORMULA

(ie co-ordinate diagram).

Suppose that
f(x) = x2 + 3x

then f(-3) = 0 ,
f(1) = 4

f: A → B

is defined by

where A = { -3, -2, -1, 0, 1}.

f(-2) = -2 , f(-1) = -2 ,

f(0) = 0 ,

NB: B = {-2, 0, 4} = the range!


Higher

Functions & Mapping
Outcome 2

A

ARROW
DIAGRAM

f(x)

B

f(-3) = 0
-3
-2
f(-2) = -2
-1
f(-1) = -2
0
f(0) = 0
1
f(1) = 4

Functions & Graphs
Outcome 2

Higher


In a GRAPH we get :

NB:

This graph consists of 5 separate points.
It is not a solid curve.

Functions & Graphs
Outcome 2

Higher


A

B

a
b
c
d

Recognising Functions

e
f
g

Not a function
two arrows leaving b!

A
a
b
c
d

B
e
f
g

YES

Functions & Graphs
Outcome 2

Higher


A

B
a
b
c
d

e
f
g

Not a function - d unused!

A
a

B
e

b
c

f

d

g

YES

Higher

Functions & Graphs
Outcome 2


Recognising Functions from Graphs

If we have a function f: R → R (R - real nos.)
then every vertical line we could draw would cut
the graph exactly once!

This basically means that every x-value has one,
and only one, corresponding y-value!

Higher

Function & Graphs
Outcome 2


Y

Function !!

x

Function & Graphs
Outcome 2

Higher


Y

Not a function !!
Cuts graph
more than once !
x must map to
one value of y
x

Higher

Functions & Graphs
Outcome 2


Y

Not a function !!
Cuts graph
more than once!

X

Higher

Functions & Graphs
Outcome 2


Y

Function !!

X

Composite Functions
Outcome 1


Higher

COMPOSITION OF FUNCTIONS
( or functions of functions )

Suppose that f and g are functions where
f:A → B
with

and

f(x) = y

where

x∈ A,

g:B → C

and

y∈ B

g(y) = z

and z∈ C.

Suppose that h is a third function where
h:A → C

with

h(x) = z .

Composite Functions

Higher

Outcome 1

ie

A

x

B

f

g

y

C

z

h
We can say that

h(x) = g(f(x))
“function of a function”


Higher

g(4)=42 +
Composite Functions1
f(2)=3x2 – 2
=17
=4
g(2)=22 + 1 Outcome 1 f(5)=5x3-2
=13
Example 1 =5
f(1)=3x1 - 2 x2 +1
Suppose that f(x) = 3x - 2 and
g(x) =
f(1)=3x1 - 2
=1
=1
(a)
g( f(2) ) =
g(4)
= 17
g(26)=262 + 1
2
g(5)=5 + 1
=677
(b)
f( g =26 ) =
(2)
f(5) = 13
(c)

f( f(1) ) =

(d)

g( g(5) )

f(1) = 1
= g(26) = 677

Composite Functions
Outcome 1

Higher


Suppose that f(x) = 3x - 2
Find formulae for

and

(a) g(f(x))

g(x) = x2 +1
(b)

f(g(x)).

(a) g(f(x)) = g(3x-2) = (3x-2)2 + 1 = 9x2 - 12x + 5
(b) f(g(x)) = f(x2 + 1)
NB:

g(f(x)) ≠

= 3(x2 + 1) - 2
f(g(x))

CHECK
g(f(2)) = 9 x 22 - 12 x 2 + 5
f(g(2)) = 3 x 22 + 1

= 13

= 3x2 + 1

in general.
= 36 - 24 + 5

= 17

As in Ex1

Composite Functions
Outcome 1

Higher


Let

h(x) = x - 3 , g(x) = x2 + 4 and k(x) = g(h(x)).

If k(x) = 8 then find the value(s) of x.
k(x) = g(h(x))
= g(x - 3)
= (x - 3)2 + 4
= x2 - 6x + 13
CHECK

Put

x2 - 6x + 13 = 8

then x2 - 6x + 5 = 0
or

(x - 5)(x - 1) = 0
So

x = 1 or x = 5

g(h(5)) = g(2) = 22 + 4 = 8

Composite Functions
Outcome 1

Higher


Choosing a Suitable Domain
(i) Suppose

f(x) =

Clearly
So
So
Hence

1 .
x2 - 4
x2 - 4 ≠ 0
x2 ≠ 4
x ≠ -2 or 2

domain = {x∈R: x ≠ -2 or 2 }

Composite Functions
Outcome 1
x=0
(ii) Suppose that g(x) = √(x2 + 2x - 8)
(0 + 4)(0 - 2)
x=3
= 8) ≥ 0
We need (x2 + 2x -negative
(3 + 4)(3 - 2)
x = -5
= positive
Suppose (x2 + 2x - 8) = 0
(-5 + 4)(-5 - 2)
= positive Then (x + 4)(x - 2) = 0


Higher

So x = -4 or x = 2

-4

2

Check values below -4 , between -4 and 2, then above 2
So

domain = { x∈R: x ≤ -4 or x ≥ 2 }

Exponential (to the power of)
Graphs
Outcome 1


Higher

Exponential Functions
A function in the form

f(x) = ax

where a > 0, a ≠ 1

is called an exponential function to base a .

Consider f(x) = 2x
x
f(x)

-3

-2

-1

0

1

2

3

/8

¼

½

1

2

4

8

1

Graph

Higher

Outcome 1

The graph is like
y = 2x
(0,1)

(1,2)

Major Points
(i) y = 2x passes through the points (0,1) & (1,2)
(ii) As x ∞ y ∞ however as x ∞ y 0 .
(iii) The graph shows a GROWTH function.

Log Graphs
Outcome 1

Higher


ie

x
y

/8

¼

-3

-2

1

½
-1

1

2

4

8

0

1

2

3

To obtain y from x we must ask the question
“What power of 2 gives us…?”
This is not practical to write in a formula so we say

y = log2x

“the logarithm to base 2 of x”
or “log base 2 of x”

Graph

Higher

The graph is like

(2,1)
Outcome 1
(1,0)

y = log2x
NB: x > 0
Major Points
(i) y = log2x passes through the points (1,0) & (2,1) .
(ii) As x  y but at a very slow rate and as x  0 y 
- .

Exponential (to the power of)
Graphs
Outcome 1


Higher

The graph of y = ax always passes through (0,1) & (1,a)
It looks like ..

Y

y = ax
(1,a)

(0,1)
x

Log Graphs
Outcome 1


Higher

The graph of y = logax always passes through (1,0) & (a,1)
It looks like ..

Y

(a,1)
(1,0)

x
y = logax

Graph Transformations
Outcome 1


Higher

We will investigate f(x) graphs of the form
1.

-f(x)

2.

f(-x)

3.

f(x) ± k

4.

f(x ± k)

5.

kf(x)

6.

f(kx)

Each moves the
Graph of f(x) in
a certain way !

Graph of -f(x) Transformations
Outcome 1


Higher

y = f(x)

y = x2

y = -f(x)

y = -x2

Mathematically
y = –f(x)
reflected f(x) in the x - axis

Outcome 1


Higher

y = f(x)

y = 2x + 3

y = -f(x)

y = -(2x + 3)

Mathematically
y = –f(x)

Outcome 1


Higher

y = f(x)

y = x3

y = -f(x)

y = -x3

Mathematically
y = –f(x)

Graph of f(-x) Transformations
Outcome 1


Higher

y = f(x)
y = f(-x)

y = x + 2
y = -x + 2

Mathematically
y = f(-x)
reflected f(x) in the y - axis

Graph of f(-x) Transformations
Outcome 1


Higher

y = f(x)

y = (x+2)2

y = f(-x)

Mathematically
y = f(-x)
reflected f(x) in the y - axis

y = (-x+2)2

Graph of f(x) ± k Transformations
Outcome 1


Higher

y = f(x)
y = f(x) ± k

y = x2
y = x2-3
y = x2 + 1

Mathematically
y = f(x) ± k
moves f(x) up or down
Depending on the value of k
+ k move up
- k move down

Graph of f(x ± k) Transformations
Mathematically
y = f(x ± k)

Higher

Outcome 1


moves f(x) to the left or right
2

y = f(x)

y = x

depending on the value of k
-k move right
+ k move left

y = f(x ± k)

y = (x-1)2
y = (x+2)2

Graph of k f(x) Transformations
Outcome 1


Higher

y = f(x)
y = k f(x)

y = x2-1
y = 2(x2-1)
y = 0. 5(x2-1)

Mathematically
y = k f(x)
Multiply y coordinate by a factor of k
k > 1  (stretch in y-axis direction)
0 < k < 1  (squash in y-axis direction)

Graph of -k f(x) Transformations
Outcome 1


Higher

y = f(x)

y = x2-1

y = k f(x)

y = -2(x2-1)
y = -0. 5(x2-1)

Mathematically
y = -k f(x)
k = -1 reflect graph in x-axis

k < -1  reflect f(x) in x-axis & multiply by a
factor k (stretch in y-axis direction)

-1 < k < 0  reflect f(x) in x-axis multiply by a
factor k (squash in y-axis direction)

Graph of f(kx) Transformations
Outcome 1


Higher

y = f(x)
y = f(kx)

y = (x-2)2
y = (2x-2)2
y = (0.5x-2)2
Mathematically
y = f(kx)

Multiply x – coordinates by 1/k

k > 1  squashes by a factor of 1/k in the x-axis direction

k < 1  stretches by a factor of 1/k in the x-axis direction

Graph of f(-kx) Transformations
Outcome 1


Higher

y = f(x)

y = (x-2)2

y = f(-kx) y = (-2x-2)2
y = (-0.5x-2)2
Mathematically
y = f(-kx)
k = -1 reflect in y-axis
k < -1  reflect & squashes by factor of 1/k in x direction
-1 < k < 0  reflect & stretches factor of 1/k in x direction

Trig Graphs
Higher

Outcome 1


The same transformation rules
apply to the basic trig graphs.
NB: If f(x) =sinx°

then 3f(x) = 3sinx°
and

f(5x) = sin5x°

Think about sin replacing f !
Also if g(x) = cosx° then g(x) –4 = cosx ° –4
and g(x+90) = cos(x+90) °
Think about cos replacing g !

Trig Graphs
Outcome 1

Higher


Sketch the graph of
If

sinx° = f(x)

then

y = sinx° - 2
sinx° - 2 = f(x) - 2

So move the sinx° graph 2 units down.

y = sinx° - 2

Trig Graphs
Outcome 1

Higher


Sketch the graph of y = cos(x - 50)°
If

cosx° = f(x)

then

cos(x - 50)° = f(x- 50)

So move the cosx° graph 50 units right.

y = cos(x - 50)°

Trig Graphs
Outcome 1

Higher


Sketch the graph of y = 3sinx°
If

sinx° = f(x)

then

3sinx° = 3f(x)

So stretch the sinx° graph 3 times vertically.

y = 3sinx°

Trig Graphs
Outcome 1


Higher

Sketch the graph of y = cos4x°
If

cosx° = f(x)

then

cos4x° = f(4x)

So squash the cosx° graph to 1/4 size horizontally

y = cos4x°

Trig Graphs

Higher

Outcome 1
Sketch the graph of y = 2sin3x°
If sinx° = f(x) then 2sin3x° = 2f(3x)
So squash the sinx° graph to 1/3 size horizontally and
also double its height.

y = 2sin3x°

Radians
Outcome 1


Higher

Radian measure is an alternative to degrees
and is based upon the ratio of

al
θ

r

θ- theta

arc length
radius

θ(radians) = a
r

Radians
Outcome 1

Higher


al = r
θ

r

If the arc length = the radius

θ (radians) = r/r = 1

If we now take a semi-circle

al

Here a = ½ of
circumference
= ½ of πd

θ
r

= πr

πr

Radians
Higher

Outcome 1


Since we have a semi-circle the angle must be 180 o.
We now get a simple connection between degrees and radians.

π (radians) = 180o
This now gives us

2π = 360o
π /2 = 90o
3π /2 = 270o
π /3 = 60o

2π /3 = 120o

π /4 = 45o

3π /4 = 135o

π /6 = 30o

5π /6 = 150o

NB: Radians are usually expressed as fractional multiples of π.

Converting
Outcome 1


Higher

÷180

then

X

π

degrees

radians
then x 180 ÷ π

The fraction button on your calculator
can be very useful here

ab/c

Converting
Outcome 1


Higher

Ex1

72o =

Ex2

330o =

Ex3

2π /9 = 2π /9 ÷ π x 180o =

Ex4

72

/180

330

X

π = 2π /5

/180 X π = 11 π /6
2

/9 X 180o = 40o

23π/18 = 23π /18 ÷ π x 180o =

23

/18 X 180o = 230o

Converting
Outcome 1

Higher


Example 5

Angular Velocity

In the days before CDs the most popular format for
music was “vinyls”.
Singles played at 45rpm while albums played at 331/3 rpm.
rpm =revolutions per minute !
Going back about 70 years an earlier version of vinyls
played at 78rpm.
Convert these record speeds into “radians per second

Converting
Outcome 1


Higher

NB:
So

So

1 revolution = 360o = 2π radians 1 min = 60 secs
45rpm = 45 X 2π or 90π radians per min
90π
=
/60 or 3π/2 radians per sec
331/3rpm = 331/3 X 2π or 662/3 π radians per min
=

So

662/3 π /60

or

10 π

/9 radians per sec

78rpm = 78 X 2π or 156π radians per min
=

/60

15π

or

13 π

/5 radians per sec

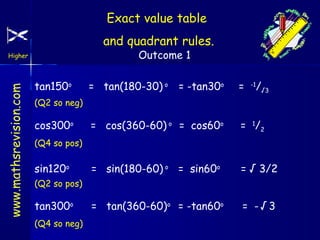
Exact value table
and quadrant rules.
Outcome 1


Higher

tan150o

= tan(180-30) o

= -tan30o

=

-1

/√3

(Q2 so neg)

cos300o

= cos(360-60) o = cos60o

= 1/2

= sin(180-60) o = sin60o

= √ 3/2

= tan(360-60)o = -tan60o

= -√3

(Q4 so pos)

sin120o
(Q2 so pos)

tan300o
(Q4 so neg)

Exact value table
and quadrant rules.
Outcome 1


Higher

Find the exact value of

cos2(5π/6) – sin2(π/6)

cos(5π/6) = cos150o = cos(180-30)o = -cos30o

= - √3 /2

(Q2 so neg)

sin(π/6)

= sin30o = 1/2

cos2(5π/6) – sin2(π/6)

= (-

√3

/2)2 – (1/2)2 = ¾ - 1/4 = 1/2

Exact value table
and quadrant rules.
Outcome 1

Higher


Prove that

sin(2 π /3) = tan (2 π /3)

cos (2 π /3)
sin(2π/3) = sin120o
= sin(180 – 60)o = sin60o =

√3

/2

cos(2 π /3) = cos120o

= cos(180 – 60)o= -cos60o= -1/2

tan(2 π /3) = tan120o

= tan(180 – 60)o= -tan60o= - √3

sin(2 π /3)
LHS =
cos (2 π /3)
= - √3

= √3/2 ÷ -1/2
= tan(2π/3) = RHS

=

√3

/2

X

-2

Trig Identities
Outcome 1


Higher

An identity is a statement which is true for all values.
eg

3x(x + 4) = 3x2 + 12x

eg

(a + b)(a – b) = a2 – b2
Trig Identities

(1)

sin2θ + cos2 θ = 1

(2)

sin θ = tan θ
cos θ

θ ≠ an odd multiple of π/2 or 90°.

Trig Identities
Outcome 1

Higher


Reason

a2 +b2 = c2

c

a

sinθo = a/c

θo

b

(1)

cosθo = b/c

sin2θo + cos2 θo =

a
b
a +b
c
+ 2 =
=
=1
2
2
2
c
c
c
c
2

2

2

2

2

Trig Identities


Higher

= tan

Outcome 1

Simply rearranging we get two other forms
sin2θ + cos2 θ = 1
sin2 θ = 1 - cos2 θ
cos2 θ = 1 - sin2 θ

Trig Identities
Outcome 1

Higher

sin θ = 5/13


Example1

where 0 < θ < π/2

Find the exact values of cos θ and tan θ .
cos2 θ = 1 - sin2 θ

Since θ is between 0 < θ < π/2

= 1 – (5/13)2

then cos θ > 0

= 1–

So

=

144

25

/169

/169

cos θ = √(144/169)
=

12

/13 or -12/13

tan θ = sinθ =
cos θ

cos θ = 12/13
5

/13 ÷ 12/13

=

5

/13

tan θ =

5

/12

X

13

/12

Trig Identities
Outcome 1


Higher

Given that cos θ = -2/ √ 5
Find sin θ and tan θ.
2

= 1 – ( /√5 )
-2

2

= 1 – 4/ 5
=

1

Hence sinθ =

=

sin θ = √( /5)
1

-1

/2

/√5

3 π

/2

sinθ < 0
tan θ = sinθ =
cos θ

/5

= 1/ √ 5 or

3 π

Since θ is between π< θ <

sin θ = 1 - cos θ
2

where π< θ <

- 1

/√5

/ √ 5 ÷ -2/ √ 5

-1

-1

/√5

X

- √5

Hence tan θ = 1/2

/2

Higher Maths

Graphs & Functions
Strategies

Click to start

Graphs & Functions

Higher

The following questions are on

Graphs & Functons
Non-calculator questions will be indicated
You will need a pencil, paper, ruler and rubber.

Click to continue

Graphs & Functions

Higher

The diagram shows the graph of a function f.
f has a minimum turning point at (0, -3) and a
point of inflexion at (-4, 2).

y = 2f(-x)

a) sketch the graph of y = f(-x).
b) On the same diagram, sketch the graph of y = 2f(-x)

a)

y
y = f(-x)

Reflect across the y axis

4
2

b)

Now scale by 2 in the y direction

-1

3

4

x

-3
-6

Previous

Quit

Quit

Hint

Next

Graphs & Functions

Higher

The diagram shows a sketch of part of
the graph of a trigonometric function
whose equation is of the form y = a sin(bx ) + c

1

2a

Determine the values of a, b and c

a is the amplitude:

a=4

b is the number of waves in 2π

1 in π
2 in 2 π

b=2

c is where the wave is centred vertically

c=1
Hint

Previous

Quit

Quit

Next

Graphs & Functions

Functions f ( x) =

Higher

1
and g ( x) = 2 x + 3 are defined on suitable domains.
x−4

a)

Find an expression for h(x) where h(x) = f(g(x)).

b)

Write down any restrictions on the domain of h.

a)

b)

2x −1 ≠ 0

1
→
2x + 3 − 4

f ( g ( x)) = f (2 x + 3)

→ x≠

1
→ h( x ) =
2x −1

1
2

Hint

Previous

Quit

Quit

Next

Graphs & Functions
a) Express

Higher

f ( x) = x 2 − 4 x + 5 in the form ( x − a ) 2 + b
(2, 1)

b) On the same diagram sketch

y=f(x)

the graph of y = f ( x)

i)
ii)

b)
5

the graph of y = 10 − f ( x )

y= 10 - f x)
(

c) Find the range of values of x for

(2, 1)

which 10 − f ( x ) is positive

a)
c)

(2, -1)

( x − 2) 2 − 4 + 5 → ( x − 2) 2 − 4 + 5
Solve:

→ ( x − 2) 2 + 1
10 − ( x − 2) 2 − 1 = 0

→ ( x − 2) 2 = 9

→ ( x − 2) = ±3

y= -f(x)

→ x = −1 or 5
Hint

10 - f(x) is positive for -1 < x < 5
Previous

Quit

Quit

Next

Graphs & Functions

Higher

The graph of a function f intersects the x-axis at (–a, 0)
and (e, 0) as shown.
There is a point of inflexion at (0, b) and a maximum turning
point at (c, d).
Sketch the graph of the derived function

f′

m is +

m is +

m is -

f′(x)
Previous

Quit

Quit

Hint

Next

Graphs & Functions

Higher

Functions f and g are defined on suitable domains by f ( x) = sin( x) and g ( x ) = 2 x
a)

Find expressions for:
i)

f ( g ( x))

ii) g ( f ( x))
b)

Solve 2 f ( g ( x)) = g ( f ( x)) for 0 ≤ x ≤ 360

a)

f ( g ( x )) = f (2 x ) = sin 2x

b)

2sin 2 x = 2sin x

→ sin 2 x − sin x = 0

→ 2sin x cos x − sin x = 0
→ sin x = 0

Previous

or

g ( f ( x)) = g (sin x) = 2sin x

cos x =

1
2

Quit

→ sin x(2 cos x − 1) = 0
x = 0°, 180°, 360°
x = 60°, 300°
Quit

Hint

Next

Graphs & Functions

Higher

The diagram shows the graphs of two quadratic
functions y = f ( x) and y = g ( x )
Both graphs have a minimum turning point at (3, 2).
Sketch the graph of

y = f ′( x)

y=f′(x)

and on the same diagram
sketch the graph of

y = g ′( x)

y=g′(x)

Hint

Previous

Quit

Quit

Next

Graphs & Functions
Functions

Higher

f ( x) = sin x, g ( x) = cos x and h( x) = x +

π
4

are defined on a suitable set of real numbers.

b) i)
ii)

g (h( x))

f (h( x ))

a) Find expressions for

f (h( x)) =

Show that

1
2

sin x +

1
2

cos x

Find a similar expression for g ( h( x))
and hence solve the equation

π
4

π
4

π
4

= sin( x + )

a)

f (h( x)) = f ( x + )

b)

sin( x + ) = sin x cos

π
4

f (h( x)) − g (h( x )) = 1 for 0 ≤ x ≤ 2π
g (h( x)) = cos( x + )

π
π
+ sin cos x
4
4

Now use exact values

Repeat for ii)
equation reduces to
Previous

2
sin x = 1
2
Quit

sin x =

Quit

2
1
=
2
2

x=

π 3π
,
4 4

Hint

Next

Graphs & Functions

Higher

A sketch of the graph of y = f(x) where ) = x 3 − 6 x 2 + 9 x
f (x

is shown.

The graph has a maximum at A and a minimum at B(3, 0)
a) Find the co-ordinates of the turning point at A.

g ( x = f ( the graph
b) Hence, )sketchx + 2) + 4 of
Indicate the co-ordinates of the turning points. There is no need to
calculate the co-ordinates of the points of intersection with the axes.
c) Write down the range of values of k for which g(x) = k has 3 real roots.

b)
c)

Differentiate

f ′( x) = 3 x 2 − 12 x + 9

when x = 1

a)

y=4

Graph is

t.p. at A is:

for SP, f′(x) = 0

x = 1 or x = 3

(1, 4)

moved 2 units to the left, and 4 units up

t.p.’s are:

(3, 0) → (1, 4)
(1, 4) → ( −1, 8)

For 3 real roots, line y = k has to cut graph at 3 points
Hint

from the graph, k ≥ 4
Previous

Quit

Quit

Next

Graphs & Functions

f ( x) = 3 − x

and

Higher
3
x

g ( x) = ,

x≠0

a) Find p( x) where p( x) = f ( g ( x ))
3
q( x) =
, x ≠ 3 find p(q ( x )) in its simplest form.
b) If
3− x

a)

p ( x) = f ( g ( x)) = f
p (q ( x)) =

b)

→

p 3  =

÷
 3− x 

3
 ÷
x

 3

3
−1÷
 3− x 
3
3− x

 9 − 3(3 − x)  3 − x

÷×
 3− x  3

Previous

→

→

Quit

3−

3
x

→

3 x −3
x

3( x −1)
x

→

 9
 3
→
− 3 ÷÷
 3− x
 3− x
3x 3 − x
×
3− x
3
Quit

→

x
Hint

Next

Graphs & Functions

Higher

Part of the graph of y = f ( x ) is shown in the diagram.
On separate diagrams sketch the graph of
y = f ( x + 1) a)

y = −2 f ( x) b)

Indicate on each graph the images of O, A, B, C, and D.

a)
b)

graph moves to the left 1 unit
graph is reflected in the x axis
graph is then scaled 2 units in the y direction

Hint

Previous

Quit

Quit

Next

Graphs & Functions

Higher

Functions f and g are defined on the set of real numbers by

f ( x) = x − 1 and g ( x) = x 2
a) Find formulae for
i)

f ( g ( x))

ii) g ( f ( x))

b) The function h is defined by h( x) = f ( g ( x)) + g ( f ( x))
2
Show that h( x) = 2 x − 2 x and sketch the graph of h.

c) Find the area enclosed between this graph and the x-axis.

a)
b)

h( x) = x − 1 + ( x − 1)

g ( f ( x)) = g ( x − 1) = ( x − 1)

f ( g ( x )) = f ( x 2 ) = x 2 − 1

c)

2

2

h( x ) = x 2 − 1 + x 2 − 2 x + 1

Graph cuts x axis at 0 and 1
Area
Previous

=

1
3

unit

Now evaluate

∫

1

0

2

→ 2x2 − 2x

2 x 2 − 2 x dx
Hint

2

Quit

Quit

Next

Graphs & Functions

Higher

The functions f and g are defined on a suitable domain by
f ( x) = x 2 − 1 and g ( x) = x 2 + 2
b) Factorise f ( g ( x ))

a) Find an expression for f ( g ( x ))

a)

f ( g ( x)) = f ( x + 2) = ( x + 2 ) − 1

b)

Difference of 2 squares

2

Simplify

2

2

→

(( x

2

)(( x

+ 2) + 1

2

)

+ 2) −1

→ ( x 2 + 3) ( x 2 + 1)

Hint

Previous

Quit

Quit

Next

Graphs & Functions

Higher

You have completed all 13 questions in this section

Previous

Quit

Quit

Back to start

Graphs & Functions

Higher

Table of exact values

30°

sin
cos
tan

Previous

45°

60°

π
6
1
2

π
4

π
3

1
2
1
2

3
2

3
2
1
3

1

1
2

3

Functions & graphs

More Related Content

What's hot (19)

Similar to Functions & graphs (20)

More from SharingIsCaring1000 (7)

Recently uploaded (20)

Functions & graphs