GeneIndex: an open source parallel program for enumerating and locating words in a genome
- 1. GeneIndex: an open source parallel program for enumerating and locating words in a genome Huian Li, David Hart, Matthias Mueller, Ulf Markward, Craig Stewart August 3, 2009 A t3
- 2. Contents • Motivation • Serial algorithm • Parallel implementation • Performance Analysis • Conclusion
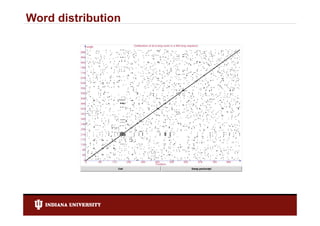
- 3. Motivation Question from a Biology professor: Given a word length, is th computational Gi dl th i the t ti l task of scanning a DNA sequence and recording th positions of all possible di the iti f ll ibl words trivial? 5 10 15 20 25 30 * * * * * * 5’ TAGCCGTGGCGGAGCCTCTTGGCTTTGTTTATTC 3’
- 4. Serial algorithm • Straightforward implementation: Binary coding for A, C, G, T. For example: A: A 00 C: 01 G: 10 T: 11 5 10 15 20 * * * * T A G C C G T G G C G G A G C C T C T T G ... 110010010110111010011010001001011101111110 ...
- 5. Serial algorithm • Given a sequence and a word length k in order to k, list all possible words, we scan the sequence once from left to right g 5 10 15 20 * * * * T A G C C G T G G C G G A G C C T C T T G ... 110010010110111010011010001001011101111110 ... T A G C 11001001 A G C C 00100101 G C C G 10010110 C T T G ... 0 011111100 ...
- 6. Serial algorithm 5 10 15 20 * * * * T A G C C G T G G C G G A G C C T C T T G ... 110010010110111010011010001001011101111110 ... T A G C 11001001 A G C C 00100101 ENCODE( AGCC ) ENCODE("AGCC") = ENCODE("TAGC") & MASK << 2 | ENCODE('C') MASK = 4k-1 – 1 = 111111 (in case of k = 4)
- 7. Serial algorithm • This essentially becomes a sorting problem since problem, each word is now converted into an integer. • Each word is associated with its position information: (Encoded Word, Position) • Sorting has to be stable so that for the same words words, their positions will be in a certain order.
- 8. Serial algorithm Implementation details: • Words & positions are stored in a long long integer (8 bytes = 64 bits) • Hash table with a linked list for each entry • S Space required f all words i given sequence i i d for ll d in i is pre-allocated, instead of malloc one by one • M tl AND OR and SHIFT LEFT operations. Mostly AND, d SHIFT-LEFT ti
- 11. Motivation for parallel implementation Another question from Biology professor: How about the human genome? Fact: Human genome includes about 3 billion DNA bases.
- 12. Parallel implementation: input Large dataset input: • Each process reads its own partition from the input file. file • Boundary area between neighboring processes has to be considered. considered agcatgcatgcatcgatcgatcgatgc atcgatgcatcgatacgatgcatgcta gacgatacgagcatgcatctagcatgc t t t t t agtagcatgcatcgatgcattagcatg ctagctagcatgctagcatgcatcgat g gcatgctagcatgctagctagcatgct g g g g g g atgcatgcatgcatcatgcatcgatcg atcgtgcaatgcatgctacgatgcatg catcagtcagcatgcatgcatcgatcg atgcatcgatcgatgcatgcatgacga t t t t t t gcaatgatgcagtcatgcatcgacgag catcgatcgatgcatgcatgcat
- 13. Parallel implementation: load balancing Computation and load balancing: 1. Each process deals with its own piece of data 2 All processes perform global sorting 2. Straightforward implementation: binary tree merge X sorting Possible solution but could be problematic Ideal solution leading to load balancing
- 14. Parallel implementation: load balancing Straightforward implementation: binary tree merge sorting AAAA: AAAC: P0 ... TTTG: TTTT: AAAA: AAAA: AAAC: AAAC: AAAC P0 ... P2 ... TTTG: TTTG: TTTT: TTTT: AAAA: 5, 9 AAAA: 19 AAAA: 4, 8 AAAA: 35 AAAC: 22 AAAC: 12 AAAC: 67 AAAC: 46 P0 ... P1 ... P2 ... P3 ... TTTG: 101 TTTG: 201 TTTG: 88 TTTG: 40 TTTT: 80 TTTT: 26 TTTT: 53 TTTT: 30
- 15. Parallel implementation: load balancing Possible solution but could be problematic: Straightforward solution: partition word range [0, 4k) equally, so each process has 4 k i 4 k i 1 , , where i = 0, 1, ..., n-1 n n AAAA: AAAA: AAAA: AAAA: AAAC: AAAC: AAAC: AAAC: CAAC: CAAC: CAAC: CAAC: CTTT: CTTT: CTTT: CTTT: ` GAAA: GAAA: GAAA: GAAA: GTTT: GTTT: GTTT: GTTT: TTTG: TTTG: TTTG: TTTG: TTTT: TTTT: TTTT: TTTT:
- 16. Parallel implementation: load balancing Implementation of the straightforward solution: • Problem is that some words occur more often than others, leading to different memory requests for different p g y q processes AAAA: 5, 9 CAAA: 19 GAAA: 4, 8 TAAA: 35, 93 AAAC: 22, 37 CAAC: 12, 47 GAAC: 67, 72 TAAC: 46 ... ... ... ... ATTG: 101 CTTG: 201 GTTG: 88 TTTG: 40, 87 ATTT: 80 CTTT: 26 GTTT: 53 TTTT: 15, 30
- 17. Parallel implementation: load balancing Ideal solution leading to load balancing: • partition the total number of words L-k+1 equally, so each p process has ( (L-k+1)/n words, where L is the length of ) , g given sequence, k is the given word length. Implementation: p 1. After each process scanned its own piece, we know that: 4 k 1 L k 1 x 0 f (Wx , Pi ) n , where i = 0 1 ..., n 1 0, 1, n-1 g [0,4k) into many small divisions 2. We divide the word range [ y with total divisions of d (where d>>n): 4k ( j 1) 1 d 1 d L k 1 j 0 f (Wx , Pi ) n , where i = 0, 1, ..., n-1 4k x j d
- 18. Parallel implementation: load balancing Implementation: 3. The number of words in each small division as below: 4k ( j 1) 1 d T (i, j ) f (W , P ) x i , where i = 0, 1, ..., n-1 4k x j d and j = 0, 1, ..., d-1 4. The total number of words in each small division across all p processes will be: 4k ( j 1) 1 n 1 d T ( j) f (W , P ) x i , where j = 0 1 ..., d-1 0, 1, d 1 i 0 4k x j d
- 19. Parallel implementation: load balancing Implementation: 5. Find an array of boundary B, such that: B ( m 1) L k 1 mT ( j ) n jB( ) where B(0)= 0, B(0<m<n) = any number in (0,d-1), and B(n)= d-1 6. Process Pi should have all words in: [B(i), [B(i) B(i+1)) , where i = 0 1 ..., n-1 0, 1, n 1.
- 20. Parallel implementation: load balancing AAAA: AAAA: AAAA: AAAA: AAAC: AAAC: AAAC: AAAC: CAAC: CAAC: CAAC: CAAC: CTTT: CTTT: CTTT: CTTT: ` GAAA: GAAA: GAAA: GAAA: GTTT: GTTT: GTTT: GTTT: TTTG: TTTG: TTTG: TTTG: TTTT: TTTT: TTTT: TTTT:
- 21. Parallel implementation: output Output: • Each process creates its own output file • If necessary, all files can concatenate into one necessary single file, while keeping the order AAAA: 5, 9, 10 AAAC: 22, 37 ... ... ... TTTG: 15, 30 TTTT: 40, 87
- 22. Testbed
- 23. Testbed specification • Consists of 768 IBM JS21 blades • On each blade: • 2 dual core PowerPC CPUs @ 2 5GHz dual-core 2.5GHz • 8 GB memory • SUSE Linux Enterprise Server 9 (ppc) • Interconnect: Myrinet • Parallel environment: MPI
- 24. Performance analysis Number of Number of D. melanogaster H. sapiens nodes processes k=6 k=25 k=6 k=25 1 1 95 23203 2 2 53 5770 4 4 29 1500 8 8 15 386 16 16 9 107 212 93672 32 32 6 32 118 24934 64 64 5 14 73 5998 128 128 9 11 59 1450 256 256 11 15 49 558 512 512 18 22 71 195 Timings of running against two datasets on BigRed using 1 PPN (SECONDS)
- 25. Performance analysis Number of Number of D. melanogaster H. sapiens nodes processes k=6 k=25 k=6 k=25 1 2 54 5958 2 4 31 1545 4 8 17 400 8 16 11 115 16 32 8 40 156 25661 32 64 6 19 101 6233 64 128 7 12 82 1506 128 256 25 16 61 576 256 512 20 27 81 198 512 1024 34 37 115 170 Timings of running against two datasets on BigRed using 2 PPN (SECONDS)
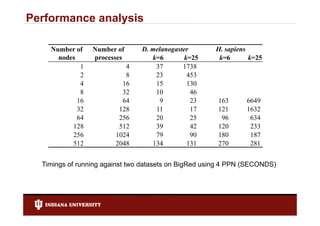
- 26. Performance analysis Number of Number of D. melanogaster H. sapiens nodes processes k=6 k=25 k=6 k=25 1 4 37 1738 2 8 23 453 4 16 15 130 8 32 10 46 16 64 9 23 163 6649 32 128 11 17 121 1632 64 256 20 25 96 634 128 512 39 42 120 233 256 1024 79 90 180 187 512 2048 134 131 270 281 Timings of running against two datasets on BigRed using 4 PPN (SECONDS)
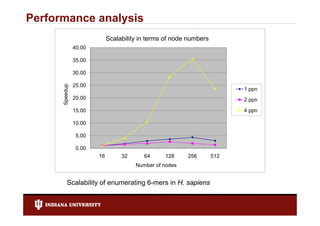
- 27. Performance analysis Scalability in terms of node numbers 40.00 35.00 30.00 25.00 up Speedu 1 ppn 20.00 2 ppn 15.00 4 ppn pp 10.00 5.00 0.00 16 32 64 128 256 512 Number of nodes Scalability of enumerating 6-mers in H. sapiens
- 28. Performance analysis Scalability in terms of node numbers 600.00 500.00 400.00 up Speedu 1 ppn 300.00 2 ppn 4 ppn pp 200.00 200 00 100.00 0.00 16 32 64 128 256 512 Number of nodes Scalability of enumerating 25-mers in H. sapiens
- 29. Conclusion • Addressed questions from the biology professor • Complicate solution aroused from memory restriction. restriction • It can handle words of length up to 30. • It can find often-repeated words, rarely-occurred , or fi d ft t d d l d even non-occurred words. • It scales relatively well on l l l ti l ll large cluster machines. l t hi • We recently developed a Java version for small DNA sequences, which was “ “our future work”. It can f ” zoom in or zoom out to view distribution and frequencies interactively. f i i t ti l
- 30. The End Thank you