General-to specific ordering of hypotheses Learning algorithms which use this ordering Version spaces and candidate elimination algorithm

MACHINE
LEARNING
17CS73
7th
Semester ISE
By: Nagesh U.B
Asst. Professor,
Dept. of ISE , AIET

Prepared by: Nagesh U.B
Chapter 1: Introduction
Wellposedlearningproblems
Designing a Learning system
Perspective and Issues in Machine Learning
Summary
Chapter 2: Concept Learning
Concept learning task
Concept learning as search
Find-S algorithm
Version space
Candidate Elimination algorithm
Inductive Bias
Summary
Module 1- Outline

Concept Learning
Inducing general functions from specific training examples is a
main issue of machine learning.
A task of acquiring a potential hypothesis (solution) that best
fits the training examples
It is the process of acquiring the definition of a general
category from given sample positive and negative training
examples of the category.
Concept Learning can seen as a problem of searching through
a predefined space of potential hypotheses for the
hypothesis that best fits the training examples.
Concept learning: Inferring a boolean-valued function from
training examples of its input and output.

Concept Learning Task
Hypothesis

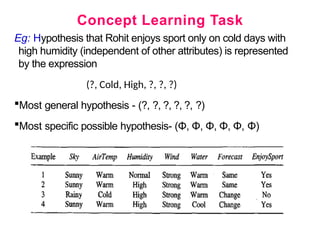
Problem is to learn the target concept.
"Days on which my friend Rohit enjoys his favorite water
sport”.
Given

Let us represent each hypothesis as a conjunction of constraints
on the instance attributes..
Each hypothesis be a vector of six constraints: Sky, AirTemp,
Humidity, Wind, Water, and Forecast.
Indicate the values for each attribute in the hypothesis as-
"?'  any value is acceptable for this attribute,
specify a single required value (e.g., Warm) for the attribute
0 by a "0" that no value is acceptable.
•If some instance x satisfies all the constraints of hypothesis h,
then h classifies x as a positive example (h(x) = 1).

Eg: Hypothesis that Rohit enjoys sport only on cold days with
high humidity (independent of other attributes) is represented
by the expression
(?, Cold, High, ?, ?, ?)
Most general hypothesis - (?, ?, ?, ?, ?, ?)
Most specific possible hypothesis- (Φ, Φ, Φ, Φ, Φ, Φ)

Notations to represent Hypothesis

Notations to represent Hypothesis
Training examples are represented as an instance x from X, along
and its target concept value c(x).
Instances for which c(x) = 1 are called positive examples.
Instances for which c(x) = 0 are called negative examples.
Therefore we write the ordered pair as: (x, c(x))
Then, each hypothesis h in H is: , h : X  {O, 1}
Now the goal of the learner is to find a hypothesis h such that
h(x) = c(x) for all x in X
where c(x) is the concept(0/1)

Inductive learning hypothesis
Our assumption is that the Fundamental assumption of
inductive learning.
• “Best hypothesis regarding unseen instances is the
hypothesis that best fits the observed training data.”
The inductive learning hypothesis.
• Any hypothesis found to approximate the target function well
over a sufficiently large set of training examples will also
approximate the target function well over other unobserved
examples.

Concept learning as search
Concept learning can be viewed as the task of searching through
a large space of hypotheses.
The goal is to find the hypothesis that best fits training
examples.
General-to-Specific Ordering of Hypotheses
h2 is more general than hl.

Find-S: Finding A Maximally Specific Hypothesis
How can we use the more-general-than partial ordering to
organize the search for a hypothesis consistent with the
observed training examples?
One way is to begin with the most specific possible hypothesis
in H, then generalize this hypothesis each time it fails to cover
an observed positive training example.
FIND-S algorithm is used for this purpose.

Find-S Algorithm
To Find Maximally Specific Hypothesis:
1. Initialize h to the most specific hypothesis in H
2. For each positive training instance x
• For each attribute constraint ai in h
•If the constraint ai is satisfied by x then do nothing
•Else replace ai in h by the next more general
constraint that is satisfied by x
3. Output Hypothesis h

Find-S Algorithm
Illustration
Consider the sequence of training examples from EnjoySport
task.
1. Initialize h to the most specific hypothesis in H, i.e
h  (Φ, Φ, Φ, Φ, Φ, Φ) ………………h1
2. Upon observing the first training example which a positive
example, it is clear that hypothesis (h1) is too specific as none of the
" Φ " constraints in h1 are satisfied by this example.
Therefore replace each constraint by the next more general
constraint that fits the example.
i.e h  (Sunny, Warm, Normal, Strong, Warm, Same) …..h2

Find-S Algorithm
3. The second training example (also positive case) forces the
algorithm to further generalize.
Therefore substitute a ‘’?’’ in place of any attribute value in h that is
not satisfied by the new example.
i.e. h  (Sunny, Warm, ?, Strong, Warm, Same) …h3
4. The third training example is a training negative example. So the
algorithm makes no change to h.
Therefore the current hypothesis h is the most specific hypothesis in
H consistent with the observed positive examples.

Find-S Algorithm
5. The fourth training example (a positive case) leads to a further
generalization of h.
Therefore substitute a ‘’?’’ in place of any attribute value in h that is
not satisfied by the new example.
i.e h  (Sunny, Warm, ?, Strong, ?, ?) …….h5

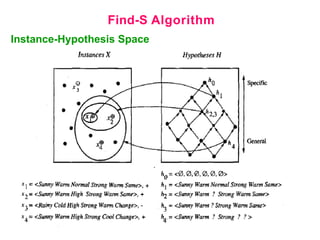
Find-S Algorithm
Instance-Hypothesis Space
FIND-S algorithm illustrates the more_general_than partial ordering to organize
the search for an acceptable hypothesis.
The search moves from most specific to progressively more general hypotheses
along one chain of the partial ordering as shown below.

Find-S Algorithm

Find-S Algorithm
At each stage the current hypothesis is the most specific hypothesis consistent
with the training examples observed up to this point (hence the name FIND-S)
The key property of the Find-S algorithm is that for hypothesis spaces
described by conjunctions of attribute constraints Find-S is guaranteed to
output the most specific hypothesis within H that is consistent with the
positive training examples

Find-S Algorithm
Find-S Drawbacks:
•Questions still left unanswered
Has the learner converged to the correct target concept?
It has no way to determine whether it has found the only hypothesis
in H consistent with the data (i.e., the correct target concept), or
whether there are many other consistent hypotheses as well.
Why prefer the most specific hypothesis?
If multiple hypotheses consistent with the training examples, FIND-
S will find the most specific. It is unclear whether we should prefer
this hypothesis over the most general.

Find-S Algorithm
Find-S Drawbacks:
•Questions still left unanswered
Are the training examples consistent?
– Training examples may contain at least some errors or noise. Such
inconsistent sets of training examples can severely mislead FIND-S,
since it ignores negative examples.
– Algorithm should detect when the training data is inconsistent and errors
What if there are several maximally specific consistent hypotheses?
– There can be several maximally specific hypotheses consistent with
the data. Find S finds only one.
– It should allow to backtrack on its choices of how to generalize the
hypothesis that the target concept lies along a different branch of the
partial ordering than the branch it has selected.

Version Spaces and Candidate Elimination
• FIND-S outputs a hypothesis from H,that is consistent with the
training examples, this is just one of many hypotheses from H
that might fit the training data equally well.
• The key idea in the CANDIDATE-ELIMINATION algorithm is to
output a description of the set of all hypotheses consistent with
the training examples.
• Applications:
– chemical mass spectroscopy
– control rules for heuristic search

• CANDIDATE-ELIMINATION algorithm finds all describable
hypotheses that are consistent with the observed training
examples.
• What is a Consistent hypotheses?
– A hypothesis is consistent with the training examples if it correctly
classifies these examples.

Notice the key difference between this definition of consistent and our
earlier definition of satisfies.
An example x is said to satisfy hypothesis h when h(x) = 1, regardless of
whether x is a positive or negative example of the target concept.
However, whether such an example is consistent with h depends on the
target concept, and in particular, whether h(x) = c(x).

CANDIDATE-ELIMINATION algorithm represents the set of all
hypotheses which are consistent with the observed training
examples.
This subset of all hypotheses is called the version space with
respect to the hypothesis space H and the training examples D,

Consistency h(x) = c(x)
x= (sunny, warm, normal, strong warm, same)
h = (sunny, warm, normal, strong warm, same)
h = (sunny, warm, ?, strong warm, same)
h = (sunny, warm, ?, strong , ?, same)

h(x) != c(x)
h = (sunny, warm, ?, strong , ?, ?)
h = (rainy, war, ?, strong , ?, same)

The List-Then-Eliminate algorithm
It is one of the way to represent the version space is simply to
list all of its members.
It first initializes the version space to contain all hypotheses in H
and then eliminates any hypothesis found inconsistent with any
training example.
The version space of candidate hypotheses thus shrinks until
ideally just one hypothesis remains which is consistent with all
the observed examples.
If insufficient data is available to narrow the version, then the
algorithm can output the entire set of hypotheses.

The List-Then-Eliminate algorithm

A More Compact Representation for Version Spaces
•The CANDIDATE-ELIMINATION algorithm works o LIST-THEN-
ELIMINATE algorithm, However the version space is represented
by most general and least general members boundary sets that
delimit the version space.
Example: consider Enjoysport concept learning problem
•FIND-S has given the hypothesis as:
h = (Sunny, Warm, ?, Strong, ?, ?)
•This is just one of six different hypotheses from H that are
consistent with these training examples.
•The other six hypotheses are-

A More Compact Representation for Version Spaces
•The CANDIDATE-ELIMINATION algorithm uses this version space
by storing its most general members (G) and its most specific
(S).
•Given only these two sets S and G, it is possible to enumerate all
members of the version space by generating the hypotheses.

Definition for G and S
•Therefore,
version space = set of hypotheses contained in G + set of
hypotheses contained in S + hypotheses that lie between G and S
in the partially ordered hypothesis space

Definition for G and S
Version space representation theorem:

Candidate Elimination Algorithm
•The CEA computes the version space containing all
hypotheses from H that are consistent with an observed
sequence of training examples.
•It begins by
 initializing the version space to the set of all hypotheses
in H; that is, G-most general hypothesis in H
 and initializing the S boundary set to contain the most
specific (least general) hypothesis

1.Initialize G to the set of maximally general hypotheses in H
2.Initialize S to the set of maximally specific hypotheses in H
3.For each training example d, do
a.If d is a positive example
Remove from G any hypothesis inconsistent with d,
For each hypothesis s in S that is not consistent with d,
• Remove s from S
• Add to S all minimal generalizations h of s such that h is consistent with
d, and some member of G is more general than h
• Remove from S, hypothesis that is more general than another hypothesis in S
b.If d is a negative example
Remove from S any hypothesis inconsistent with d
For each hypothesis g in G that is not consistent with d
• Remove g from G
• Add to G all minimal specializations h of g such that h is consistent with
d, and some member of S is more specific than h
• Remove from G any hypothesis that is less general than another in G

Illustration

Iteration-1

Iteration-2

Iteration-3

Iteration-4

Illustration
The final version space for the EnjoySport concept learning
problem

Example Final Version Space:
After processing these four examples, the boundary sets S4
and G4 delimit the version space of all hypotheses consistent
with the set of incrementally observed training examples.
The entire version space, including those hypotheses
bounded by S4 and G4.
This learned version space is independent of the sequence in
which the training examples are presented.
As further training data is encountered, the S and G
boundaries will move monotonically closer to each other.

Will Candidate-Elimination Algorithm Converge
to Correct Hypothesis?
• The version space learned by the Candidate-Elimination Algorithm
will converge toward the hypothesis that correctly describes the
target concept, provided-
– There are no errors in the training examples, and
– there is some hypothesis in H that correctly describes the target concept.
• What will happen if the training data contains errors?
– The algorithm removes the correct target concept from the version space.
– S and G boundary sets eventually converge to an empty version space if
sufficient additional training data is available.
– Such an empty version space indicates that there is no hypothesis in H consistent with
all observed training examples.
• A similar symptom will appear when the training examples are
correct, but the target concept cannot be described in the hypothesis
representation.
– e.g., if the target concept is a disjunction of feature attributes and the hypothesis
space supports only conjunctive descriptions

What Training Example Should the Learner Request Next?
• We have assumed that training examples are provided to the learner
by some external teacher.
• This is not sufficient to gather more experience.
• Solution is to do more experiments
• If the learner is allowed to conduct experiments then it can construct
new instances and then obtains the correct classification for this
instance from an external oracle (e.g., nature or a teacher).
– This process can be called as query .
• For the “EnjoySport" version space,
– What would be a good query?

What Training Example Should the Learner Request Next?
• The learner should try to discriminate among the
alternative competing hypotheses in its current version
space.
– It should choose an instance that would be classified positive by some of these
hypotheses, but negative by others.
– Example: <Sunny, Warm, Normal, Light, Warm, Same>
– This instance satisfies three of the six hypotheses in the current version space .
– If the trainer classifies this as positive example, the S boundary of the version space
can then be generalized and is a negative example, the G boundary can then be
specialized.
• In general, the optimal query strategy for a concept learner is to generate instances
that satisfy exactly half the hypotheses in the current version space.
• Then the size of the version space is reduces by half with each new example,
• Therefore the total number of experiments needed to reach correct target concept is:
log2 |VS| 

How Can Partially Learned Concepts Be Used?
• The indication of multiple hypotheses in version space is the target
concept has not yet been fully learned (partially learned).
• But it is still possible to classify certain new examples as if the
target concept had been uniquely identified. How it is possible???
• Considering the followings new instances to be classified:

 Instance A - is classified as a positive instance by every
hypothesis in the current version space.
– Since all the hypotheses in the version space classified this as a positive
instance, the learner can classify instance A as if it had already converged to
correct target concept.
• Instance B – is classified as a negative instance by every
hypothesis in the version space.
– This instance can therefore be safely classified as negative using our partially
learned concept.

• Instance C - Half of the version space hypotheses classify as
positive and half classify it as negative.
– Thus, the learner cannot classify this example with confidence until further
training examples are available.
• Instance D - is classified as positive by two of the version
space hypotheses and negative by the other four
hypotheses.
– In this case we have less confidence in the classification.
– One approach we could follow is to output the majority vote
indicating how close the vote was. Then it will be a negative
example.

Inductive Bias
• The CEA will converge to correct target concept only if it is
given with accurate training examples and its initial hypothesis
space contains the target concept.
• What if the target concept is not contained in the hypothesis
space?
• Can we avoid this difficulty by using a hypothesis space that
contains every possible hypothesis?
• How does the size of this hypothesis space influence the ability of
the algorithm to generalize to unobserved instances?
• How does the size of the hypothesis space influence the number
of training examples that must be observed?
Fundamental Questions for Inductive Inference

Inductive Bias - A Biased Hypothesis Space
• In EnjoySport example, we restricted the hypothesis space to include
only conjunctions of attribute values.
– Because of this restriction, the hypothesis space is unable to represent even
simple disjunctive target concepts such as "Sky = Sunny or Sky = Cloudy."
• From first two examples  S2 : <?, Warm, Normal, Strong, Cool, Change>
• This is inconsistent with third examples, and there are no hypotheses
consistent with these three examples
PROBLEM: We have biased the learner to consider only conjunctive hypotheses.
 We require a more expressive hypothesis space.

Inductive Bias
• The solution to this problem is to have a hypothesis space capable of
representing every teachable concept.
– So we need every possible instance.
– Every possible subset of the instances X is called as power set of X.
• What is the size of the hypothesis space H (the power set of X) ?
– In EnjoySport, the size of the instance space X is 96.
– The size of the power set of X is 2|X|  The size of H is 296
Note:- Our conjunctive hypothesis space is able to represent only 973 of
these hypotheses. Therefore it is a very biased hypothesis space
An Unbiased Learner

Inductive Bias
• Let the hypothesis space H to be the power set of X.
– A hypothesis can be represented with disjunctions, conjunctions, and
negations of our earlier hypotheses.
– The target concept "Sky = Sunny or Sky = Cloudy" could then be
described as-
<Sunny, ?, ?, ?, ?, ?>  <Cloudy, ?, ?, ?, ?, ?>
NEW PROBLEM: Our concept learning algorithm is now completely
unable to generalize beyond the observed examples.
Ex: suppose we present three positive examples (xl, x2, x3) and two negative examples
(x4, x5) to the learner. Then-
S : { x1  x2  x3 }and G : {  (x4  x5) }  NO GENERALIZATION
– Therefore, the only examples that will be unambiguously classified by S and G
are the observed training examples themselves.
An Unbiased Learner continued..

Inductive Bias
• Fundamental Property of Inductive Inference is:
“A learner that makes no a priori assumptions regarding the identity of the
target concept has no rational basis for classifying any unseen instances“
Inductive Leap:
• A learner should be able to generalize training data using prior assumptions
(B) in order to classify unseen instances.
• The generalization is known as inductive leap and our prior
assumptions are the inductive bias of the learner.
• Inductive Bias (prior assumptions) of Candidate-Elimination Algorithm is that
the target concept can be represented by a conjunction of attribute values, the
target concept is contained in the hypothesis space and training examples are
correct.
The Futility of Bias free Learning:

Inductive Bias
Consider a concept learning algorithm L for the set of instances X.
• Let c be an arbitrary concept defined over X, and
• let Dc = {<x , c(x)>} be an arbitrary set of training examples of c.
• Let L(xi, Dc) denote the classification assigned to the instance xi
by L
After training on the data Dc.
The inductive bias of L is any minimal set of assertions B such that
for any target concept c and corresponding training examples Dc the
following formula holds.
Formal Definition

Inductive Bias – Three Learning Algorithms
ROTE-LEARNER: Learning corresponds simply to storing each observed
training example in memory. Subsequent instances are classified by looking
them up in memory. If the instance is found in memory, the stored
classification is returned. Otherwise, the system refuses to classify the new
instance.
Inductive Bias: No inductive bias
CANDIDATE-ELIMINATION: New instances are classified only in the case where
all members of the current version space agree on the classification. Otherwise, the
system refuses to classify the new instance.
Inductive Bias: the target concept can be represented in its hypothesis space.
FIND-S: This algorithm, described earlier, finds the most specific hypothesis
consistent with the training examples. It then uses this hypothesis to classify all
subsequent instances.
Inductive Bias: the target concept can be represented in its hypothesis space, and all
instances are negative instances unless the opposite is entailed by its other
know1edge.

General-to specific ordering of hypotheses Learning algorithms which use this ordering Version spaces and candidate elimination algorithm

More Related Content

Similar to General-to specific ordering of hypotheses Learning algorithms which use this ordering Version spaces and candidate elimination algorithm (20)

Recently uploaded (20)

General-to specific ordering of hypotheses Learning algorithms which use this ordering Version spaces and candidate elimination algorithm