SlideShare a Scribd company logo

Geometry Section 2-7

J
Jimbo Lamb

This document defines key terms and concepts related to parallel lines and transversals, including: - A transversal is a line that intersects two other lines at two different points. - Interior angles are formed between the two lines, while exterior angles are outside the lines. - Alternate interior angles, corresponding angles, and other angle relationships are defined. - Examples demonstrate identifying angle relationships and using properties of parallel lines to calculate unknown angle measures.

Education
1 of 63
Download to read offline
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
SECTION 2-7 Parallel Lines and Transversals
ESSENTIAL QUESTIONS How do you identify the relationships between two lines or two planes? How do you name angle pairs formed by parallel lines and transversals?
VOCABULARY 1. Transversal: 2. Interior Angles: 3. Exterior Angles: 4. Consecutive Interior Angles:
VOCABULARY 1. Transversal: A line that intersects two other coplanar lines at two different points 2. Interior Angles: 3. Exterior Angles: 4. Consecutive Interior Angles:
VOCABULARY 1. Transversal: A line that intersects two other coplanar lines at two different points 2. Interior Angles: Angles that are formed in the region between two lines being intersected by a transversal 3. Exterior Angles: 4. Consecutive Interior Angles:
VOCABULARY 1. Transversal: A line that intersects two other coplanar lines at two different points 2. Interior Angles: Angles that are formed in the region between two lines being intersected by a transversal 3. Exterior Angles: Angles that are formed in the region outside of the two lines being intersected by a transversal 4. Consecutive Interior Angles:
VOCABULARY 1. Transversal: A line that intersects two other coplanar lines at two different points 2. Interior Angles: Angles that are formed in the region between two lines being intersected by a transversal 3. Exterior Angles: Angles that are formed in the region outside of the two lines being intersected by a transversal 4. Consecutive Interior Angles: Interior angles that are on the same side of the transversal, thus being “next” to each other
VOCABULARY 5. Alternate Interior Angles: 6. Alternate Exterior Angles: 7. Corresponding Angles: 8. Parallel Lines:
VOCABULARY 5. Alternate Interior Angles: Nonadjacent interior angles that are on opposite sides of the transversal 6. Alternate Exterior Angles: 7. Corresponding Angles: 8. Parallel Lines:
VOCABULARY 5. Alternate Interior Angles: Nonadjacent interior angles that are on opposite sides of the transversal 6. Alternate Exterior Angles: 7. Corresponding Angles: 8. Parallel Lines: Nonadjacent exterior angles that are on opposite sides of the transversal
VOCABULARY 5. Alternate Interior Angles: Nonadjacent interior angles that are on opposite sides of the transversal 6. Alternate Exterior Angles: 7. Corresponding Angles: 8. Parallel Lines: Nonadjacent exterior angles that are on opposite sides of the transversal Angles that are on the same side of the transversal and on the same side of the lines being intersected by the transversal; these angles have the same position
VOCABULARY 5. Alternate Interior Angles: Nonadjacent interior angles that are on opposite sides of the transversal 6. Alternate Exterior Angles: 7. Corresponding Angles: 8. Parallel Lines: Two or more lines in the same plane that do not intersect Nonadjacent exterior angles that are on opposite sides of the transversal Angles that are on the same side of the transversal and on the same side of the lines being intersected by the transversal; these angles have the same position
VOCABULARY 9. Skew Lines: 10. Parallel Planes:
VOCABULARY 9. Skew Lines: Two or more lines that are in different planes and do not intersect 10. Parallel Planes:
VOCABULARY 9. Skew Lines: Two or more lines that are in different planes and do not intersect 10. Parallel Planes: Two or more planes that do not intersect
EXAMPLE 1 Identify each of the following using the box. a. All segments parallel to BC b. A segment that is skew to EH c. A plane that is parallel to plane ABG
EXAMPLE 1 Identify each of the following using the box. a. All segments parallel to BC FG, AD, EH b. A segment that is skew to EH c. A plane that is parallel to plane ABG
EXAMPLE 1 Identify each of the following using the box. a. All segments parallel to BC FG, AD, EH b. A segment that is skew to EH DC, CF, AB, or BG c. A plane that is parallel to plane ABG
EXAMPLE 1 Identify each of the following using the box. a. All segments parallel to BC FG, AD, EH b. A segment that is skew to EH DC, CF, AB, or BG c. A plane that is parallel to plane ABG Plane DEC
EXAMPLE 2 Refer to the figure below. Classify the relationship between each pair of angles as alternate interior, alternate exterior, corresponding, or consecutive interior angles. a. ∠2 and ∠6 b. ∠1 and ∠7
EXAMPLE 2 Refer to the figure below. Classify the relationship between each pair of angles as alternate interior, alternate exterior, corresponding, or consecutive interior angles. a. ∠2 and ∠6 b. ∠1 and ∠7 Corresponding Angles
EXAMPLE 2 Refer to the figure below. Classify the relationship between each pair of angles as alternate interior, alternate exterior, corresponding, or consecutive interior angles. a. ∠2 and ∠6 b. ∠1 and ∠7 Corresponding Angles Alternate Exterior Angles
EXAMPLE 2 Refer to the figure below. Classify the relationship between each pair of angles as alternate interior, alternate exterior, corresponding, or consecutive interior angles. c. ∠3 and ∠8 d. ∠3 and ∠5
EXAMPLE 2 Refer to the figure below. Classify the relationship between each pair of angles as alternate interior, alternate exterior, corresponding, or consecutive interior angles. c. ∠3 and ∠8 d. ∠3 and ∠5 Consecutive Interior Angles
EXAMPLE 2 Refer to the figure below. Classify the relationship between each pair of angles as alternate interior, alternate exterior, corresponding, or consecutive interior angles. c. ∠3 and ∠8 d. ∠3 and ∠5 Consecutive Interior Angles Alternate Interior Angles
EXAMPLE 3 The driveways at a bus station are shown. Identify the transversal connecting each pair of angles in the figure. Then classify the relationship between each pair of angles. a. ∠1 and ∠2 b. ∠2 and ∠3
EXAMPLE 3 The driveways at a bus station are shown. Identify the transversal connecting each pair of angles in the figure. Then classify the relationship between each pair of angles. a. ∠1 and ∠2 b. ∠2 and ∠3 v; Corresponding
EXAMPLE 3 The driveways at a bus station are shown. Identify the transversal connecting each pair of angles in the figure. Then classify the relationship between each pair of angles. a. ∠1 and ∠2 b. ∠2 and ∠3 v; Corresponding v; Alternate Interior
EXAMPLE 3 The driveways at a bus station are shown. Identify the transversal connecting each pair of angles in the figure. Then classify the relationship between each pair of angles. c. ∠4 and ∠5
EXAMPLE 3 The driveways at a bus station are shown. Identify the transversal connecting each pair of angles in the figure. Then classify the relationship between each pair of angles. c. ∠4 and ∠5 y; Consecutive Interior
POSTULATES AND THEOREMS CORRESPONDING ANGLES POSTULATE
POSTULATES AND THEOREMS CORRESPONDING ANGLES POSTULATE IF TWO PARALLEL LINES ARE CUT BY A TRANSVERSAL, THEN EACH PAIR OF CORRESPONDING ANGLES IS CONGRUENT.
POSTULATES AND THEOREMS CORRESPONDING ANGLES POSTULATE IF TWO PARALLEL LINES ARE CUT BY A TRANSVERSAL, THEN EACH PAIR OF CORRESPONDING ANGLES IS CONGRUENT. ∠1 ≅ ∠5
POSTULATES AND THEOREMS ALTERNATE INTERIOR ANGLES THEOREM
POSTULATES AND THEOREMS ALTERNATE INTERIOR ANGLES THEOREM IF TWO PARALLEL LINES ARE CUT BY A TRANSVERSAL, THEN EACH PAIR OF ALTERNATE INTERIOR ANGLES IS CONGRUENT.
POSTULATES AND THEOREMS ALTERNATE INTERIOR ANGLES THEOREM IF TWO PARALLEL LINES ARE CUT BY A TRANSVERSAL, THEN EACH PAIR OF ALTERNATE INTERIOR ANGLES IS CONGRUENT. ∠4 ≅ ∠6
POSTULATES AND THEOREMS CONSECUTIVE INTERIOR ANGLES THEOREM
POSTULATES AND THEOREMS CONSECUTIVE INTERIOR ANGLES THEOREM IF TWO PARALLEL LINES ARE CUT BY A TRANSVERSAL, THEN EACH PAIR OF CONSECUTIVE INTERIOR ANGLES IS SUPPLEMENTARY.
POSTULATES AND THEOREMS CONSECUTIVE INTERIOR ANGLES THEOREM IF TWO PARALLEL LINES ARE CUT BY A TRANSVERSAL, THEN EACH PAIR OF CONSECUTIVE INTERIOR ANGLES IS SUPPLEMENTARY. ∠4 AND ∠5 ARE SUPPLEMENTARY
POSTULATES AND THEOREMS ALTERNATE EXTERIOR ANGLES THEOREM
POSTULATES AND THEOREMS ALTERNATE EXTERIOR ANGLES THEOREM IF TWO PARALLEL LINES ARE CUT BY A TRANSVERSAL, THEN EACH PAIR OF ALTERNATE EXTERIOR ANGLES IS CONGRUENT.
POSTULATES AND THEOREMS ALTERNATE EXTERIOR ANGLES THEOREM IF TWO PARALLEL LINES ARE CUT BY A TRANSVERSAL, THEN EACH PAIR OF ALTERNATE EXTERIOR ANGLES IS CONGRUENT. ∠2 ≅ ∠7
EXAMPLE 4 IN THE FIGURE, m∠4 = 51°. FIND THE MEASURE OF EACH ANGLE. GIVE A JUSTIFICATION TO YOUR ANSWER. a. m∠2 b. m∠3 c. m∠6
EXAMPLE 4 IN THE FIGURE, m∠4 = 51°. FIND THE MEASURE OF EACH ANGLE. GIVE A JUSTIFICATION TO YOUR ANSWER. a. m∠2 51°; VERTICAL ANGLES THM. WITH ∠4 b. m∠3 c. m∠6
EXAMPLE 4 IN THE FIGURE, m∠4 = 51°. FIND THE MEASURE OF EACH ANGLE. GIVE A JUSTIFICATION TO YOUR ANSWER. a. m∠2 51°; VERTICAL ANGLES THM. WITH ∠4 b. m∠3 129°; SUPPLEMENTARY THM. WITH ∠4 c. m∠6
EXAMPLE 4 IN THE FIGURE, m∠4 = 51°. FIND THE MEASURE OF EACH ANGLE. GIVE A JUSTIFICATION TO YOUR ANSWER. a. m∠2 51°; VERTICAL ANGLES THM. WITH ∠4 b. m∠3 129°; SUPPLEMENTARY THM. WITH ∠4 c. m∠6 51°; ALTERNATE INTERIOR ANGLES THM. WITH ∠4
EXAMPLE 5 USE THE FIGURE, IN WHICH a||b, m∠2 = 125°, AND c||d||e, TO FIND THE MEASURE OF EACH NUMBERED ANGLE. PROVIDE A REASON FOR THE ANSWER FOR EACH MEASURE.
EXAMPLE 5 USE THE FIGURE, IN WHICH a||b, m∠2 = 125°, AND c||d||e, TO FIND THE MEASURE OF EACH NUMBERED ANGLE. PROVIDE A REASON FOR THE ANSWER FOR EACH MEASURE. m∠1 = 125°; VERTICAL ANGLES THM. WITH ∠2
EXAMPLE 5 USE THE FIGURE, IN WHICH a||b, m∠2 = 125°, AND c||d||e, TO FIND THE MEASURE OF EACH NUMBERED ANGLE. PROVIDE A REASON FOR THE ANSWER FOR EACH MEASURE. m∠1 = 125°; VERTICAL ANGLES THM. WITH ∠2 m∠3 = 55°; CONSECUTIVE INTERIOR ANGLES THM. WITH ∠2
EXAMPLE 5 USE THE FIGURE, IN WHICH a||b, m∠2 = 125°, AND c||d||e, TO FIND THE MEASURE OF EACH NUMBERED ANGLE. PROVIDE A REASON FOR THE ANSWER FOR EACH MEASURE. m∠1 = 125°; VERTICAL ANGLES THM. WITH ∠2 m∠3 = 55°; CONSECUTIVE INTERIOR ANGLES THM. WITH ∠2 m∠4 = 125°; CONSECUTIVE INTERIOR ANGLES THM. WITH ∠3
EXAMPLE 5 USE THE FIGURE, IN WHICH a||b, m∠2 = 125°, AND c||d||e, TO FIND THE MEASURE OF EACH NUMBERED ANGLE. PROVIDE A REASON FOR THE ANSWER FOR EACH MEASURE. m∠1 = 125°; VERTICAL ANGLES THM. WITH ∠2 m∠3 = 55°; CONSECUTIVE INTERIOR ANGLES THM. WITH ∠2 m∠4 = 125°; CONSECUTIVE INTERIOR ANGLES THM. WITH ∠3 m∠5 = 55°; SUPPLEMENTARY ANGLES THM. WITH ∠4
EXAMPLE 6 USE THE FIGURE TO FIND THE INDICATED VARIABLE. EXPLAIN YOUR REASONING. a. IF m∠2 = (2x ­ 10)° AND m∠6 = (x + 15)°, FIND x.
EXAMPLE 6 USE THE FIGURE TO FIND THE INDICATED VARIABLE. EXPLAIN YOUR REASONING. a. IF m∠2 = (2x ­ 10)° AND m∠6 = (x + 15)°, FIND x. 2x ­ 10 = x + 15
EXAMPLE 6 USE THE FIGURE TO FIND THE INDICATED VARIABLE. EXPLAIN YOUR REASONING. a. IF m∠2 = (2x ­ 10)° AND m∠6 = (x + 15)°, FIND x. 2x ­ 10 = x + 15 ­x ­x
EXAMPLE 6 USE THE FIGURE TO FIND THE INDICATED VARIABLE. EXPLAIN YOUR REASONING. a. IF m∠2 = (2x ­ 10)° AND m∠6 = (x + 15)°, FIND x. 2x ­ 10 = x + 15 ­x ­x +10+10
EXAMPLE 6 USE THE FIGURE TO FIND THE INDICATED VARIABLE. EXPLAIN YOUR REASONING. a. IF m∠2 = (2x ­ 10)° AND m∠6 = (x + 15)°, FIND x. 2x ­ 10 = x + 15 ­x ­x +10+10 x = 25
EXAMPLE 6 USE THE FIGURE TO FIND THE INDICATED VARIABLE. EXPLAIN YOUR REASONING. a. IF m∠2 = (2x ­ 10)° AND m∠6 = (x + 15)°, FIND x. 2x ­ 10 = x + 15 ­x ­x +10+10 x = 25 SINCE THE ANGLES ARE CORRESPONDING, THEY ARE CONGRUENT BY THE CORRESPONDING ANGLES POSTULATE, SO THEIR MEASURES ARE EQUA BY THE DEF. OF CONGRUENT ANGLES.
EXAMPLE 6 USE THE FIGURE TO FIND THE INDICATED VARIABLE. EXPLAIN YOUR REASONING. b. IF m∠7 = [4(y ­ 25)]° AND m∠1 = (4y)°, FIND y.
EXAMPLE 6 USE THE FIGURE TO FIND THE INDICATED VARIABLE. EXPLAIN YOUR REASONING. b. IF m∠7 = [4(y ­ 25)]° AND m∠1 = (4y)°, FIND y. 4(y ­ 25) + 4y = 180
EXAMPLE 6 USE THE FIGURE TO FIND THE INDICATED VARIABLE. EXPLAIN YOUR REASONING. b. IF m∠7 = [4(y ­ 25)]° AND m∠1 = (4y)°, FIND y. 4(y ­ 25) + 4y = 180 4y ­ 100 + 4y = 180
EXAMPLE 6 USE THE FIGURE TO FIND THE INDICATED VARIABLE. EXPLAIN YOUR REASONING. b. IF m∠7 = [4(y ­ 25)]° AND m∠1 = (4y)°, FIND y. 4(y ­ 25) + 4y = 180 4y ­ 100 + 4y = 180 8y ­ 100 = 180
EXAMPLE 6 USE THE FIGURE TO FIND THE INDICATED VARIABLE. EXPLAIN YOUR REASONING. b. IF m∠7 = [4(y ­ 25)]° AND m∠1 = (4y)°, FIND y. 4(y ­ 25) + 4y = 180 4y ­ 100 + 4y = 180 8y ­ 100 = 180 8y = 280
EXAMPLE 6 USE THE FIGURE TO FIND THE INDICATED VARIABLE. EXPLAIN YOUR REASONING. b. IF m∠7 = [4(y ­ 25)]° AND m∠1 = (4y)°, FIND y. 4(y ­ 25) + 4y = 180 4y ­ 100 + 4y = 180 8y ­ 100 = 180 8y = 280 y = 35

More Related Content

PDF
Geometry Section 3-1 1112
Jimbo Lamb
 
PPT
GD_Geometry_In_My_World
MHS
 
PPT
LF_Geometry_In_My_World
MHS
 
PPT
Geometry in My World (KP)
MHS
 
PPT
Geometry in My World (MT)
MHS
 
PPT
Geometry in My World (JG)
MHS
 
PPT
Geometry in My World (BK)
MHS
 
PPT
Geometry In My World (JL)
MHS
 
Geometry Section 3-1 1112
Jimbo Lamb
 
GD_Geometry_In_My_World
MHS
 
LF_Geometry_In_My_World
MHS
 
Geometry in My World (KP)
MHS
 
Geometry in My World (MT)
MHS
 
Geometry in My World (JG)
MHS
 
Geometry in My World (BK)
MHS
 
Geometry In My World (JL)
MHS
 

Similar to Geometry Section 2-7 (20)

PPTX
Section 2 1 definitions and theorems
Janae B. Tull
 
PPTX
Parallel Lines Initial Definitions and Theorems
k3smith_ODU
 
PPTX
Section2 1definitionsandtheorems
Janae B. Tull
 
PPT
Parallel lines and transversals
Leslie Amoguis
 
PDF
2.4.1 Parallel Lines and Transversals
smiller5
 
PPTX
Parallel lines and Transversal ( Math 8 )
CristineJoyAlolor1
 
PDF
Module 3 geometric relations
dionesioable
 
PPT
Geometry unit 3.1.3.3
Mark Ryder
 
PDF
3.2 Parallel Lines and Transversals
smiller5
 
PDF
1.3.2A Parallel Lines
smiller5
 
PPTX
MWA10 5.3 NonParallel Lines
OLCTeacher
 
PPTX
Sample SIM math 7 3rd quarter
lyka may berlan
 
PDF
1.4.1 Parallel Lines and Transversals
smiller5
 
PPTX
Math 7 geometry 04 angles, parallel lines, and transversals - grade 7
Gilbert Joseph Abueg
 
PDF
transversal-180614065616.pdfrrrrrrrrrrrr
ElsieGumoc
 
PPTX
Planes, Lines and Transversals
Fidelfo Moral
 
PPT
angle facts.ppt angle facts angle facts angle facts
ambin5978
 
PPTX
Angles Formed by Parallel Lines Cut by a Transversal
Bella Jao
 
PDF
Chapter 1 lines and angles ii [compatibility mode]
Khusaini Majid
 
DOCX
Self learning material maths
komalranawat
 
Section 2 1 definitions and theorems
Janae B. Tull
 
Parallel Lines Initial Definitions and Theorems
k3smith_ODU
 
Section2 1definitionsandtheorems
Janae B. Tull
 
Parallel lines and transversals
Leslie Amoguis
 
2.4.1 Parallel Lines and Transversals
smiller5
 
Parallel lines and Transversal ( Math 8 )
CristineJoyAlolor1
 
Module 3 geometric relations
dionesioable
 
Geometry unit 3.1.3.3
Mark Ryder
 
3.2 Parallel Lines and Transversals
smiller5
 
1.3.2A Parallel Lines
smiller5
 
MWA10 5.3 NonParallel Lines
OLCTeacher
 
Sample SIM math 7 3rd quarter
lyka may berlan
 
1.4.1 Parallel Lines and Transversals
smiller5
 
Math 7 geometry 04 angles, parallel lines, and transversals - grade 7
Gilbert Joseph Abueg
 
transversal-180614065616.pdfrrrrrrrrrrrr
ElsieGumoc
 
Planes, Lines and Transversals
Fidelfo Moral
 
angle facts.ppt angle facts angle facts angle facts
ambin5978
 
Angles Formed by Parallel Lines Cut by a Transversal
Bella Jao
 
Chapter 1 lines and angles ii [compatibility mode]
Khusaini Majid
 
Self learning material maths
komalranawat
 
Ad

More from Jimbo Lamb (20)

PDF
Geometry Section 1-5
Jimbo Lamb
 
PDF
Geometry Section 1-4
Jimbo Lamb
 
PDF
Geometry Section 1-3
Jimbo Lamb
 
PDF
Geometry Section 1-2
Jimbo Lamb
 
PDF
Geometry Section 1-2
Jimbo Lamb
 
PDF
Geometry Section 1-1
Jimbo Lamb
 
PDF
Algebra 2 Section 5-3
Jimbo Lamb
 
PDF
Algebra 2 Section 5-2
Jimbo Lamb
 
PDF
Algebra 2 Section 5-1
Jimbo Lamb
 
PDF
Algebra 2 Section 4-9
Jimbo Lamb
 
PDF
Algebra 2 Section 4-8
Jimbo Lamb
 
PDF
Algebra 2 Section 4-6
Jimbo Lamb
 
PDF
Geometry Section 6-6
Jimbo Lamb
 
PDF
Geometry Section 6-5
Jimbo Lamb
 
PDF
Geometry Section 6-4
Jimbo Lamb
 
PDF
Geometry Section 6-3
Jimbo Lamb
 
PDF
Geometry Section 6-2
Jimbo Lamb
 
PDF
Geometry Section 6-1
Jimbo Lamb
 
PDF
Algebra 2 Section 4-5
Jimbo Lamb
 
PDF
Algebra 2 Section 4-4
Jimbo Lamb
 
Geometry Section 1-5
Jimbo Lamb
 
Geometry Section 1-4
Jimbo Lamb
 
Geometry Section 1-3
Jimbo Lamb
 
Geometry Section 1-2
Jimbo Lamb
 
Geometry Section 1-2
Jimbo Lamb
 
Geometry Section 1-1
Jimbo Lamb
 
Algebra 2 Section 5-3
Jimbo Lamb
 
Algebra 2 Section 5-2
Jimbo Lamb
 
Algebra 2 Section 5-1
Jimbo Lamb
 
Algebra 2 Section 4-9
Jimbo Lamb
 
Algebra 2 Section 4-8
Jimbo Lamb
 
Algebra 2 Section 4-6
Jimbo Lamb
 
Geometry Section 6-6
Jimbo Lamb
 
Geometry Section 6-5
Jimbo Lamb
 
Geometry Section 6-4
Jimbo Lamb
 
Geometry Section 6-3
Jimbo Lamb
 
Geometry Section 6-2
Jimbo Lamb
 
Geometry Section 6-1
Jimbo Lamb
 
Algebra 2 Section 4-5
Jimbo Lamb
 
Algebra 2 Section 4-4
Jimbo Lamb
 
Ad

Recently uploaded (20)

PPTX
Cell Types and Its function , kingdom of life
ClaireMangundayao1
 
PDF
Chinmaya Tiranga quiz Grand Finale.pdf
Nitin Suresh
 
PPTX
UNIT III MENTAL HEALTH NURSING ASSESSMENT
Sonali Gupta
 
PDF
Practical Manual AGRO-233 Principles and Practices of Natural Farming
MilindKhedekar2
 
PDF
RMMM.pdf make it easy to upload and study
sajedul2
 
PDF
A GUIDE TO GENETICS FOR UNDERGRADUATE MEDICAL STUDENTS
DrBincy A. S
 
PPTX
Tissue processing ( HISTOPATHOLOGICAL TECHNIQUE
mathiasmelwyn7
 
PPTX
Introduction to Building Materials
Mrunali Vasava
 
PDF
Black Hat USA 2025 - Micro ICS Summit - ICS/OT Threat Landscape
Chris Sistrunk
 
PDF
ChatGPT for Dummies - Pam Baker Ccesa007.pdf
Demetrio Ccesa Rayme
 
DOC
Soft-furnishing-By-Architect-A.F.M.Mohiuddin-Akhand.doc
ArchitectAFMMohiuddi
 
PDF
advance database management system book.pdf
hinamannan364
 
PPTX
Orientation - ARALprogram of Deped to the Parents.pptx
JeromeTamayoSantiago1
 
PDF
LDMMIA Reiki Yoga Finals Review Spring Summer
LDMMia Reiki Lectures
 
PDF
Computing-Curriculum for Schools in Ghana
abigailanane203
 
PDF
IGGE1 Understanding the Self1234567891011
rhea22labucay
 
PDF
1_English_Language_Set_2.pdf probationary
emailjagmeetsingh9
 
PPTX
Unit 4 Skeletal System.ppt.pptxopresentatiom
umair817123
 
PDF
Hazard Identification & Risk Assessment .pdf
estagiarioprotegesms
 
PDF
Weekly quiz Compilation Jan -July 25.pdf
Nitin Suresh
 
Cell Types and Its function , kingdom of life
ClaireMangundayao1
 
Chinmaya Tiranga quiz Grand Finale.pdf
Nitin Suresh
 
UNIT III MENTAL HEALTH NURSING ASSESSMENT
Sonali Gupta
 
Practical Manual AGRO-233 Principles and Practices of Natural Farming
MilindKhedekar2
 
RMMM.pdf make it easy to upload and study
sajedul2
 
A GUIDE TO GENETICS FOR UNDERGRADUATE MEDICAL STUDENTS
DrBincy A. S
 
Tissue processing ( HISTOPATHOLOGICAL TECHNIQUE
mathiasmelwyn7
 
Introduction to Building Materials
Mrunali Vasava
 
Black Hat USA 2025 - Micro ICS Summit - ICS/OT Threat Landscape
Chris Sistrunk
 
ChatGPT for Dummies - Pam Baker Ccesa007.pdf
Demetrio Ccesa Rayme
 
Soft-furnishing-By-Architect-A.F.M.Mohiuddin-Akhand.doc
ArchitectAFMMohiuddi
 
advance database management system book.pdf
hinamannan364
 
Orientation - ARALprogram of Deped to the Parents.pptx
JeromeTamayoSantiago1
 
LDMMIA Reiki Yoga Finals Review Spring Summer
LDMMia Reiki Lectures
 
Computing-Curriculum for Schools in Ghana
abigailanane203
 
IGGE1 Understanding the Self1234567891011
rhea22labucay
 
1_English_Language_Set_2.pdf probationary
emailjagmeetsingh9
 
Unit 4 Skeletal System.ppt.pptxopresentatiom
umair817123
 
Hazard Identification & Risk Assessment .pdf
estagiarioprotegesms
 
Weekly quiz Compilation Jan -July 25.pdf
Nitin Suresh
 

Geometry Section 2-7

  • 1. SECTION 2-7 Parallel Lines and Transversals
  • 2. ESSENTIAL QUESTIONS How do you identify the relationships between two lines or two planes? How do you name angle pairs formed by parallel lines and transversals?
  • 3. VOCABULARY 1. Transversal: 2. Interior Angles: 3. Exterior Angles: 4. Consecutive Interior Angles:
  • 4. VOCABULARY 1. Transversal: A line that intersects two other coplanar lines at two different points 2. Interior Angles: 3. Exterior Angles: 4. Consecutive Interior Angles:
  • 5. VOCABULARY 1. Transversal: A line that intersects two other coplanar lines at two different points 2. Interior Angles: Angles that are formed in the region between two lines being intersected by a transversal 3. Exterior Angles: 4. Consecutive Interior Angles:
  • 6. VOCABULARY 1. Transversal: A line that intersects two other coplanar lines at two different points 2. Interior Angles: Angles that are formed in the region between two lines being intersected by a transversal 3. Exterior Angles: Angles that are formed in the region outside of the two lines being intersected by a transversal 4. Consecutive Interior Angles:
  • 7. VOCABULARY 1. Transversal: A line that intersects two other coplanar lines at two different points 2. Interior Angles: Angles that are formed in the region between two lines being intersected by a transversal 3. Exterior Angles: Angles that are formed in the region outside of the two lines being intersected by a transversal 4. Consecutive Interior Angles: Interior angles that are on the same side of the transversal, thus being “next” to each other
  • 8. VOCABULARY 5. Alternate Interior Angles: 6. Alternate Exterior Angles: 7. Corresponding Angles: 8. Parallel Lines:
  • 9. VOCABULARY 5. Alternate Interior Angles: Nonadjacent interior angles that are on opposite sides of the transversal 6. Alternate Exterior Angles: 7. Corresponding Angles: 8. Parallel Lines:
  • 10. VOCABULARY 5. Alternate Interior Angles: Nonadjacent interior angles that are on opposite sides of the transversal 6. Alternate Exterior Angles: 7. Corresponding Angles: 8. Parallel Lines: Nonadjacent exterior angles that are on opposite sides of the transversal
  • 11. VOCABULARY 5. Alternate Interior Angles: Nonadjacent interior angles that are on opposite sides of the transversal 6. Alternate Exterior Angles: 7. Corresponding Angles: 8. Parallel Lines: Nonadjacent exterior angles that are on opposite sides of the transversal Angles that are on the same side of the transversal and on the same side of the lines being intersected by the transversal; these angles have the same position
  • 12. VOCABULARY 5. Alternate Interior Angles: Nonadjacent interior angles that are on opposite sides of the transversal 6. Alternate Exterior Angles: 7. Corresponding Angles: 8. Parallel Lines: Two or more lines in the same plane that do not intersect Nonadjacent exterior angles that are on opposite sides of the transversal Angles that are on the same side of the transversal and on the same side of the lines being intersected by the transversal; these angles have the same position
  • 13. VOCABULARY 9. Skew Lines: 10. Parallel Planes:
  • 14. VOCABULARY 9. Skew Lines: Two or more lines that are in different planes and do not intersect 10. Parallel Planes:
  • 15. VOCABULARY 9. Skew Lines: Two or more lines that are in different planes and do not intersect 10. Parallel Planes: Two or more planes that do not intersect
  • 16. EXAMPLE 1 Identify each of the following using the box. a. All segments parallel to BC b. A segment that is skew to EH c. A plane that is parallel to plane ABG
  • 17. EXAMPLE 1 Identify each of the following using the box. a. All segments parallel to BC FG, AD, EH b. A segment that is skew to EH c. A plane that is parallel to plane ABG
  • 18. EXAMPLE 1 Identify each of the following using the box. a. All segments parallel to BC FG, AD, EH b. A segment that is skew to EH DC, CF, AB, or BG c. A plane that is parallel to plane ABG
  • 19. EXAMPLE 1 Identify each of the following using the box. a. All segments parallel to BC FG, AD, EH b. A segment that is skew to EH DC, CF, AB, or BG c. A plane that is parallel to plane ABG Plane DEC
  • 20. EXAMPLE 2 Refer to the figure below. Classify the relationship between each pair of angles as alternate interior, alternate exterior, corresponding, or consecutive interior angles. a. ∠2 and ∠6 b. ∠1 and ∠7
  • 21. EXAMPLE 2 Refer to the figure below. Classify the relationship between each pair of angles as alternate interior, alternate exterior, corresponding, or consecutive interior angles. a. ∠2 and ∠6 b. ∠1 and ∠7 Corresponding Angles
  • 22. EXAMPLE 2 Refer to the figure below. Classify the relationship between each pair of angles as alternate interior, alternate exterior, corresponding, or consecutive interior angles. a. ∠2 and ∠6 b. ∠1 and ∠7 Corresponding Angles Alternate Exterior Angles
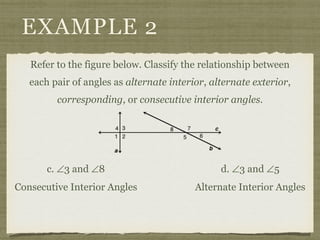
  • 23. EXAMPLE 2 Refer to the figure below. Classify the relationship between each pair of angles as alternate interior, alternate exterior, corresponding, or consecutive interior angles. c. ∠3 and ∠8 d. ∠3 and ∠5
  • 24. EXAMPLE 2 Refer to the figure below. Classify the relationship between each pair of angles as alternate interior, alternate exterior, corresponding, or consecutive interior angles. c. ∠3 and ∠8 d. ∠3 and ∠5 Consecutive Interior Angles
  • 25. EXAMPLE 2 Refer to the figure below. Classify the relationship between each pair of angles as alternate interior, alternate exterior, corresponding, or consecutive interior angles. c. ∠3 and ∠8 d. ∠3 and ∠5 Consecutive Interior Angles Alternate Interior Angles
  • 26. EXAMPLE 3 The driveways at a bus station are shown. Identify the transversal connecting each pair of angles in the figure. Then classify the relationship between each pair of angles. a. ∠1 and ∠2 b. ∠2 and ∠3
  • 27. EXAMPLE 3 The driveways at a bus station are shown. Identify the transversal connecting each pair of angles in the figure. Then classify the relationship between each pair of angles. a. ∠1 and ∠2 b. ∠2 and ∠3 v; Corresponding
  • 28. EXAMPLE 3 The driveways at a bus station are shown. Identify the transversal connecting each pair of angles in the figure. Then classify the relationship between each pair of angles. a. ∠1 and ∠2 b. ∠2 and ∠3 v; Corresponding v; Alternate Interior
  • 29. EXAMPLE 3 The driveways at a bus station are shown. Identify the transversal connecting each pair of angles in the figure. Then classify the relationship between each pair of angles. c. ∠4 and ∠5
  • 30. EXAMPLE 3 The driveways at a bus station are shown. Identify the transversal connecting each pair of angles in the figure. Then classify the relationship between each pair of angles. c. ∠4 and ∠5 y; Consecutive Interior
  • 32. POSTULATES AND THEOREMS CORRESPONDING ANGLES POSTULATE IF TWO PARALLEL LINES ARE CUT BY A TRANSVERSAL, THEN EACH PAIR OF CORRESPONDING ANGLES IS CONGRUENT.
  • 33. POSTULATES AND THEOREMS CORRESPONDING ANGLES POSTULATE IF TWO PARALLEL LINES ARE CUT BY A TRANSVERSAL, THEN EACH PAIR OF CORRESPONDING ANGLES IS CONGRUENT. ∠1 ≅ ∠5
  • 34. POSTULATES AND THEOREMS ALTERNATE INTERIOR ANGLES THEOREM
  • 35. POSTULATES AND THEOREMS ALTERNATE INTERIOR ANGLES THEOREM IF TWO PARALLEL LINES ARE CUT BY A TRANSVERSAL, THEN EACH PAIR OF ALTERNATE INTERIOR ANGLES IS CONGRUENT.
  • 36. POSTULATES AND THEOREMS ALTERNATE INTERIOR ANGLES THEOREM IF TWO PARALLEL LINES ARE CUT BY A TRANSVERSAL, THEN EACH PAIR OF ALTERNATE INTERIOR ANGLES IS CONGRUENT. ∠4 ≅ ∠6
  • 37. POSTULATES AND THEOREMS CONSECUTIVE INTERIOR ANGLES THEOREM
  • 38. POSTULATES AND THEOREMS CONSECUTIVE INTERIOR ANGLES THEOREM IF TWO PARALLEL LINES ARE CUT BY A TRANSVERSAL, THEN EACH PAIR OF CONSECUTIVE INTERIOR ANGLES IS SUPPLEMENTARY.
  • 39. POSTULATES AND THEOREMS CONSECUTIVE INTERIOR ANGLES THEOREM IF TWO PARALLEL LINES ARE CUT BY A TRANSVERSAL, THEN EACH PAIR OF CONSECUTIVE INTERIOR ANGLES IS SUPPLEMENTARY. ∠4 AND ∠5 ARE SUPPLEMENTARY
  • 40. POSTULATES AND THEOREMS ALTERNATE EXTERIOR ANGLES THEOREM
  • 41. POSTULATES AND THEOREMS ALTERNATE EXTERIOR ANGLES THEOREM IF TWO PARALLEL LINES ARE CUT BY A TRANSVERSAL, THEN EACH PAIR OF ALTERNATE EXTERIOR ANGLES IS CONGRUENT.
  • 42. POSTULATES AND THEOREMS ALTERNATE EXTERIOR ANGLES THEOREM IF TWO PARALLEL LINES ARE CUT BY A TRANSVERSAL, THEN EACH PAIR OF ALTERNATE EXTERIOR ANGLES IS CONGRUENT. ∠2 ≅ ∠7
  • 43. EXAMPLE 4 IN THE FIGURE, m∠4 = 51°. FIND THE MEASURE OF EACH ANGLE. GIVE A JUSTIFICATION TO YOUR ANSWER. a. m∠2 b. m∠3 c. m∠6
  • 44. EXAMPLE 4 IN THE FIGURE, m∠4 = 51°. FIND THE MEASURE OF EACH ANGLE. GIVE A JUSTIFICATION TO YOUR ANSWER. a. m∠2 51°; VERTICAL ANGLES THM. WITH ∠4 b. m∠3 c. m∠6
  • 45. EXAMPLE 4 IN THE FIGURE, m∠4 = 51°. FIND THE MEASURE OF EACH ANGLE. GIVE A JUSTIFICATION TO YOUR ANSWER. a. m∠2 51°; VERTICAL ANGLES THM. WITH ∠4 b. m∠3 129°; SUPPLEMENTARY THM. WITH ∠4 c. m∠6
  • 46. EXAMPLE 4 IN THE FIGURE, m∠4 = 51°. FIND THE MEASURE OF EACH ANGLE. GIVE A JUSTIFICATION TO YOUR ANSWER. a. m∠2 51°; VERTICAL ANGLES THM. WITH ∠4 b. m∠3 129°; SUPPLEMENTARY THM. WITH ∠4 c. m∠6 51°; ALTERNATE INTERIOR ANGLES THM. WITH ∠4
  • 47. EXAMPLE 5 USE THE FIGURE, IN WHICH a||b, m∠2 = 125°, AND c||d||e, TO FIND THE MEASURE OF EACH NUMBERED ANGLE. PROVIDE A REASON FOR THE ANSWER FOR EACH MEASURE.
  • 48. EXAMPLE 5 USE THE FIGURE, IN WHICH a||b, m∠2 = 125°, AND c||d||e, TO FIND THE MEASURE OF EACH NUMBERED ANGLE. PROVIDE A REASON FOR THE ANSWER FOR EACH MEASURE. m∠1 = 125°; VERTICAL ANGLES THM. WITH ∠2
  • 49. EXAMPLE 5 USE THE FIGURE, IN WHICH a||b, m∠2 = 125°, AND c||d||e, TO FIND THE MEASURE OF EACH NUMBERED ANGLE. PROVIDE A REASON FOR THE ANSWER FOR EACH MEASURE. m∠1 = 125°; VERTICAL ANGLES THM. WITH ∠2 m∠3 = 55°; CONSECUTIVE INTERIOR ANGLES THM. WITH ∠2
  • 50. EXAMPLE 5 USE THE FIGURE, IN WHICH a||b, m∠2 = 125°, AND c||d||e, TO FIND THE MEASURE OF EACH NUMBERED ANGLE. PROVIDE A REASON FOR THE ANSWER FOR EACH MEASURE. m∠1 = 125°; VERTICAL ANGLES THM. WITH ∠2 m∠3 = 55°; CONSECUTIVE INTERIOR ANGLES THM. WITH ∠2 m∠4 = 125°; CONSECUTIVE INTERIOR ANGLES THM. WITH ∠3
  • 51. EXAMPLE 5 USE THE FIGURE, IN WHICH a||b, m∠2 = 125°, AND c||d||e, TO FIND THE MEASURE OF EACH NUMBERED ANGLE. PROVIDE A REASON FOR THE ANSWER FOR EACH MEASURE. m∠1 = 125°; VERTICAL ANGLES THM. WITH ∠2 m∠3 = 55°; CONSECUTIVE INTERIOR ANGLES THM. WITH ∠2 m∠4 = 125°; CONSECUTIVE INTERIOR ANGLES THM. WITH ∠3 m∠5 = 55°; SUPPLEMENTARY ANGLES THM. WITH ∠4
  • 52. EXAMPLE 6 USE THE FIGURE TO FIND THE INDICATED VARIABLE. EXPLAIN YOUR REASONING. a. IF m∠2 = (2x ­ 10)° AND m∠6 = (x + 15)°, FIND x.
  • 53. EXAMPLE 6 USE THE FIGURE TO FIND THE INDICATED VARIABLE. EXPLAIN YOUR REASONING. a. IF m∠2 = (2x ­ 10)° AND m∠6 = (x + 15)°, FIND x. 2x ­ 10 = x + 15
  • 54. EXAMPLE 6 USE THE FIGURE TO FIND THE INDICATED VARIABLE. EXPLAIN YOUR REASONING. a. IF m∠2 = (2x ­ 10)° AND m∠6 = (x + 15)°, FIND x. 2x ­ 10 = x + 15 ­x ­x
  • 55. EXAMPLE 6 USE THE FIGURE TO FIND THE INDICATED VARIABLE. EXPLAIN YOUR REASONING. a. IF m∠2 = (2x ­ 10)° AND m∠6 = (x + 15)°, FIND x. 2x ­ 10 = x + 15 ­x ­x +10+10
  • 56. EXAMPLE 6 USE THE FIGURE TO FIND THE INDICATED VARIABLE. EXPLAIN YOUR REASONING. a. IF m∠2 = (2x ­ 10)° AND m∠6 = (x + 15)°, FIND x. 2x ­ 10 = x + 15 ­x ­x +10+10 x = 25
  • 57. EXAMPLE 6 USE THE FIGURE TO FIND THE INDICATED VARIABLE. EXPLAIN YOUR REASONING. a. IF m∠2 = (2x ­ 10)° AND m∠6 = (x + 15)°, FIND x. 2x ­ 10 = x + 15 ­x ­x +10+10 x = 25 SINCE THE ANGLES ARE CORRESPONDING, THEY ARE CONGRUENT BY THE CORRESPONDING ANGLES POSTULATE, SO THEIR MEASURES ARE EQUA BY THE DEF. OF CONGRUENT ANGLES.
  • 58. EXAMPLE 6 USE THE FIGURE TO FIND THE INDICATED VARIABLE. EXPLAIN YOUR REASONING. b. IF m∠7 = [4(y ­ 25)]° AND m∠1 = (4y)°, FIND y.
  • 59. EXAMPLE 6 USE THE FIGURE TO FIND THE INDICATED VARIABLE. EXPLAIN YOUR REASONING. b. IF m∠7 = [4(y ­ 25)]° AND m∠1 = (4y)°, FIND y. 4(y ­ 25) + 4y = 180
  • 60. EXAMPLE 6 USE THE FIGURE TO FIND THE INDICATED VARIABLE. EXPLAIN YOUR REASONING. b. IF m∠7 = [4(y ­ 25)]° AND m∠1 = (4y)°, FIND y. 4(y ­ 25) + 4y = 180 4y ­ 100 + 4y = 180
  • 61. EXAMPLE 6 USE THE FIGURE TO FIND THE INDICATED VARIABLE. EXPLAIN YOUR REASONING. b. IF m∠7 = [4(y ­ 25)]° AND m∠1 = (4y)°, FIND y. 4(y ­ 25) + 4y = 180 4y ­ 100 + 4y = 180 8y ­ 100 = 180
  • 62. EXAMPLE 6 USE THE FIGURE TO FIND THE INDICATED VARIABLE. EXPLAIN YOUR REASONING. b. IF m∠7 = [4(y ­ 25)]° AND m∠1 = (4y)°, FIND y. 4(y ­ 25) + 4y = 180 4y ­ 100 + 4y = 180 8y ­ 100 = 180 8y = 280
  • 63. EXAMPLE 6 USE THE FIGURE TO FIND THE INDICATED VARIABLE. EXPLAIN YOUR REASONING. b. IF m∠7 = [4(y ­ 25)]° AND m∠1 = (4y)°, FIND y. 4(y ­ 25) + 4y = 180 4y ­ 100 + 4y = 180 8y ­ 100 = 180 8y = 280 y = 35