Graphs > Discrete structures , Data Structures & Algorithums
- 2. Minimum Spanning Tree: Prim's Algorithm Prim's algorithm for finding an MST is a greedy algorithm. Start by selecting an arbitrary vertex, include it into the current MST. Grow the current MST by inserting into it the vertex closest to one of the vertices already in current MST.
- 3. Minimum Spanning Tree Problem: given a connected, undirected, weighted graph, find a spanning tree using edges that minimize the total weight 6 4 5 9 14 2 10 15 3 8
- 4. Prim’s Algorithm MST-Prim(G, w, r) Q = V[G]; for each u ∈ Q key[u] = ∞; key[r] = 0; p[r] = NULL; while (Q not empty) u = ExtractMin(Q); for each v ∈ Adj[u] if (v ∈ Q and w(u,v) < key[v]) p[v] = u; key[v] = w(u,v);
- 5. Prim’s Algorithm MST-Prim(G, w, r) 6 Q = V[G]; 5 for each u ∈ Q key[u] = ∞; key[r] = 0; 14 10 p[r] = NULL; while (Q not empty) u = ExtractMin(Q); for each v ∈ Adj[u] 3 if (v ∈ Q and w(u,v) < key[v]) Run p[v] = u; key[v] = w(u,v); 4 9 2 15 8 on example graph
- 6. Prim’s Algorithm MST-Prim(G, w, r) ∞ 6 Q = V[G]; 5 for each u ∈ Q ∞ key[u] = ∞; key[r] = 0; 14 10 p[r] = NULL; while (Q not empty) ∞ u = ExtractMin(Q); for each v ∈ Adj[u] 3 ∞ if (v ∈ Q and w(u,v) < key[v]) Run p[v] = u; key[v] = w(u,v); 4 ∞ 9 ∞ 2 ∞ 15 8 on example graph ∞
- 7. Prim’s Algorithm MST-Prim(G, w, r) ∞ 6 Q = V[G]; 5 for each u ∈ Q ∞ key[u] = ∞; key[r] = 0; 14 10 p[r] = NULL; while (Q not empty) 0 r u = ExtractMin(Q); for each v ∈ Adj[u] 3 ∞ if (v ∈ Q and w(u,v) < key[v]) Pick p[v] = u; key[v] = w(u,v); 4 ∞ 9 ∞ 2 ∞ 8 a start vertex r 15 ∞
- 8. Prim’s Algorithm MST-Prim(G, w, r) ∞ 6 4 Q = V[G]; 5 for each u ∈ Q ∞ ∞ key[u] = ∞; key[r] = 0; 14 2 10 p[r] = NULL; while (Q not empty) 0 ∞ u u = ExtractMin(Q); for each v ∈ Adj[u] 3 8 ∞ if (v ∈ Q and w(u,v) < key[v]) Black vertices have been p[v] = u; key[v] = w(u,v); 9 15 ∞ ∞ removed from Q
- 9. Prim’s Algorithm MST-Prim(G, w, r) ∞ 6 4 Q = V[G]; 5 for each u ∈ Q ∞ key[u] = ∞; 14 key[r] = 0; 10 p[r] = NULL; 0 u while (Q not empty) u = ExtractMin(Q); 3 8 3 for each v ∈ Adj[u] if (v ∈ Q and w(u,v) < key[v]) p[v] = u; Black arrows key[v] = w(u,v); ∞ 9 ∞ 2 ∞ 15 ∞ indicate parent pointers
- 10. Prim’s Algorithm 6 ∞ 5 MST-Prim(G, w, r) 14 Q = V[G]; for each u ∈ Q 14 10 key[u] = ∞; key[r] = 0; 0 u p[r] = NULL; 3 3 while (Q not empty) u = ExtractMin(Q); for each v ∈ Adj[u] if (v ∈ Q and w(u,v) < key[v]) p[v] = u; key[v] = w(u,v); 4 ∞ 9 ∞ 2 ∞ 8 15 ∞
- 11. Prim’s Algorithm 6 ∞ 5 MST-Prim(G, w, r) 14 Q = V[G]; for each u ∈ Q 14 10 key[u] = ∞; key[r] = 0; 0 p[r] = NULL; 3 3 while (Q not empty) u u = ExtractMin(Q); for each v ∈ Adj[u] if (v ∈ Q and w(u,v) < key[v]) p[v] = u; key[v] = w(u,v); 4 ∞ 9 ∞ 2 ∞ 8 15 ∞
- 12. Prim’s Algorithm 6 ∞ 5 MST-Prim(G, w, r) 14 Q = V[G]; for each u ∈ Q 14 10 key[u] = ∞; key[r] = 0; 0 p[r] = NULL; 3 3 while (Q not empty) u u = ExtractMin(Q); for each v ∈ Adj[u] if (v ∈ Q and w(u,v) < key[v]) p[v] = u; key[v] = w(u,v); 4 ∞ 9 ∞ 2 8 8 15 ∞
- 13. Prim’s Algorithm 6 ∞ 5 MST-Prim(G, w, r) 10 Q = V[G]; for each u ∈ Q 14 10 key[u] = ∞; key[r] = 0; 0 p[r] = NULL; 3 3 while (Q not empty) u u = ExtractMin(Q); for each v ∈ Adj[u] if (v ∈ Q and w(u,v) < key[v]) p[v] = u; key[v] = w(u,v); 4 ∞ 9 ∞ 2 8 8 15 ∞
- 14. Prim’s Algorithm 6 ∞ 5 MST-Prim(G, w, r) 10 Q = V[G]; for each u ∈ Q 14 10 key[u] = ∞; key[r] = 0; 0 p[r] = NULL; 3 3 while (Q not empty) u = ExtractMin(Q); for each v ∈ Adj[u] if (v ∈ Q and w(u,v) < key[v]) p[v] = u; key[v] = w(u,v); 4 ∞ 9 ∞ 2 8 8 u 15 ∞
- 15. Prim’s Algorithm 6 ∞ 5 MST-Prim(G, w, r) 10 Q = V[G]; for each u ∈ Q 14 10 key[u] = ∞; key[r] = 0; 0 p[r] = NULL; 3 3 while (Q not empty) u = ExtractMin(Q); for each v ∈ Adj[u] if (v ∈ Q and w(u,v) < key[v]) p[v] = u; key[v] = w(u,v); 4 9 2 ∞ 2 8 8 u 15 ∞
- 16. Prim’s Algorithm 6 ∞ 5 MST-Prim(G, w, r) 10 Q = V[G]; for each u ∈ Q 14 10 key[u] = ∞; key[r] = 0; 0 p[r] = NULL; 3 3 while (Q not empty) u = ExtractMin(Q); for each v ∈ Adj[u] if (v ∈ Q and w(u,v) < key[v]) p[v] = u; key[v] = w(u,v); 4 9 2 ∞ 2 8 8 u 15 15
- 17. Prim’s Algorithm 6 ∞ 5 MST-Prim(G, w, r) 10 Q = V[G]; for each u ∈ Q 14 10 key[u] = ∞; key[r] = 0; 0 p[r] = NULL; 3 3 while (Q not empty) u = ExtractMin(Q); for each v ∈ Adj[u] if (v ∈ Q and w(u,v) < key[v]) p[v] = u; key[v] = w(u,v); u 4 9 2 ∞ 2 8 8 15 15
- 18. Prim’s Algorithm 6 4 5 MST-Prim(G, w, r) 10 Q = V[G]; for each u ∈ Q 14 10 key[u] = ∞; key[r] = 0; 0 p[r] = NULL; 3 3 while (Q not empty) u = ExtractMin(Q); for each v ∈ Adj[u] if (v ∈ Q and w(u,v) < key[v]) p[v] = u; key[v] = w(u,v); u 4 9 2 ∞ 2 8 8 15 15
- 19. Prim’s Algorithm 6 4 5 MST-Prim(G, w, r) 5 Q = V[G]; for each u ∈ Q 14 10 key[u] = ∞; key[r] = 0; 0 p[r] = NULL; 3 3 while (Q not empty) u = ExtractMin(Q); for each v ∈ Adj[u] if (v ∈ Q and w(u,v) < key[v]) p[v] = u; key[v] = w(u,v); u 4 9 2 ∞ 2 8 8 15 15
- 20. Prim’s Algorithm 6 4 5 MST-Prim(G, w, r) 5 Q = V[G]; for each u ∈ Q 14 10 key[u] = ∞; key[r] = 0; 0 p[r] = NULL; 3 3 while (Q not empty) u = ExtractMin(Q); for each v ∈ Adj[u] if (v ∈ Q and w(u,v) < key[v]) p[v] = u; key[v] = w(u,v); u 4 9 2 9 2 8 8 15 15
- 21. Prim’s Algorithm 6 4 5 MST-Prim(G, w, r) 5 Q = V[G]; for each u ∈ Q 14 10 key[u] = ∞; key[r] = 0; 0 p[r] = NULL; 3 3 while (Q not empty) u = ExtractMin(Q); for each v ∈ Adj[u] if (v ∈ Q and w(u,v) < key[v]) p[v] = u; key[v] = w(u,v); 4 u 9 2 9 2 8 8 15 15
- 22. Prim’s Algorithm u 6 4 5 MST-Prim(G, w, r) 5 Q = V[G]; for each u ∈ Q 14 10 key[u] = ∞; key[r] = 0; 0 p[r] = NULL; 3 3 while (Q not empty) u = ExtractMin(Q); for each v ∈ Adj[u] if (v ∈ Q and w(u,v) < key[v]) p[v] = u; key[v] = w(u,v); 4 9 2 9 2 8 8 15 15
- 23. Prim’s Algorithm 6 4 5 MST-Prim(G, w, r) 5 Q = V[G]; for each u ∈ Q 14 10 key[u] = ∞; key[r] = 0; 0 p[r] = NULL; 3 3 while (Q not empty) u = ExtractMin(Q); for each v ∈ Adj[u] if (v ∈ Q and w(u,v) < key[v]) p[v] = u; key[v] = w(u,v); u 4 9 2 9 2 8 8 15 15
- 24. Prim’s Algorithm 6 4 5 MST-Prim(G, w, r) 5 Q = V[G]; for each u ∈ Q 14 10 key[u] = ∞; key[r] = 0; 0 p[r] = NULL; 3 3 while (Q not empty) u = ExtractMin(Q); for each v ∈ Adj[u] if (v ∈ Q and w(u,v) < key[v]) p[v] = u; key[v] = w(u,v); 4 9 2 u 2 8 8 9 15 15
- 25. Review: Prim’s Algorithm MST-Prim(G, w, r) Q = V[G]; for each u ∈ Q key[u] = ∞; key[r] = 0; p[r] = NULL; while (Q not empty) u = ExtractMin(Q); for each v ∈ Adj[u] if (v ∈ Q and w(u,v) < key[v]) p[v] = u; key[v] = w(u,v);
- 26. Dijkstra’s Algorithm Similar to (BFS) Breadth-First Search Grow a tree gradually, advancing from vertices taken from a queue Also similar to Prim’s algorithm for MST Use a priority queue keyed on d[v]
- 27. Shortest Path for Weighted Graphs Given a graph G = (V, E) with edge costs c(e), and a vertex s ∈ V, find the shortest (lowest cost) path from s to every vertex in V Assume: only positive edge costs
- 28. Dijkstra’s Algorithm for Single Source Shortest Path Similar to breadth-first search, but uses a heap instead of a queue: Always select (expand) the vertex that has a lowest-cost path to the start vertex Correctly handles the case where the lowest-cost (shortest) path to a vertex is not the one with fewest edges
- 29. Dijkstra, Edsger Wybe Legendary figure in computer science; was a professor at University of Texas. Supported teaching introductory computer courses without computers (pencil and paper programming) Supposedly wouldn’t (until very late in life) read his e-mail; so, his staff had to print out messages and put them in his box. E.W. Dijkstra (1930-2002) 1972 Turning Award Winner, Programming Languages, semaphores, and …
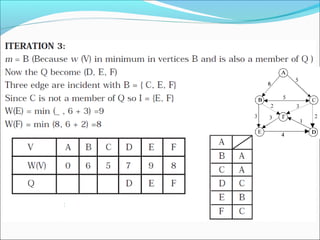
- 37. Final Table
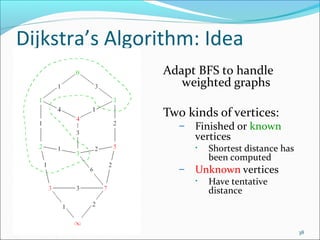
- 38. Dijkstra’s Algorithm: Idea Adapt BFS to handle weighted graphs Two kinds of vertices: – Finished or known vertices • – Shortest distance has been computed Unknown vertices • Have tentative distance 38
- 39. Dijkstra’s Algorithm: Idea At each step: Pick closest unknown vertex 2) Add it to known vertices 3) Update distances 1) 39
- 40. Dijkstra’s Algorithm: Pseudocode Initialize the cost of each node to ∞ Initialize the cost of the source to 0 While there are unknown nodes left in the graph Select an unknown node b with the lowest cost Mark b as known For each node a adjacent to b a’s cost = min(a’s old cost, b’s cost + cost of (b, a)) a’s prev path node = b 40
- 41. Important Features Once a vertex is made known, the cost of the shortest path to that node is known While a vertex is still not known, another shorter path to it might still be found 41
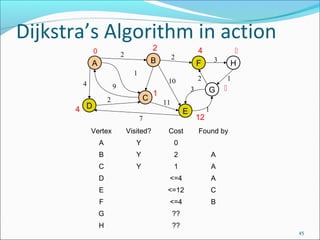
- 42. Dijkstra’s Algorithm in action 0 2 2 B A 2 D C 3 E Vertex Visited? Cost A ?? F ?? G ?? H ?? Found by ?? E ?? D 1 ?? C 0 B 1 G 11 7 H 2 10 9 3 F 1 4 42
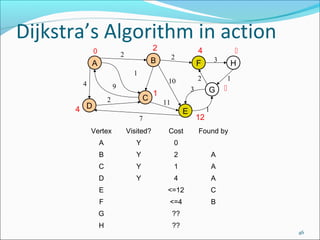
- 43. Dijkstra’s Algorithm in action 0 2 2 2 B A C 2 4 D 3 1 E Vertex Visited? Cost A Y 1 G 11 7 H 2 10 9 3 F 1 4 1 Found by 0 B <=2 A C <=1 A D <=4 A E ?? F ?? G ?? H ?? 43
- 44. Dijkstra’s Algorithm in action 0 2 2 2 B A C 2 4 D 3 1 E Vertex Visited? Cost A Y 1 G 11 7 H 2 10 9 3 F 1 4 12 1 0 B Found by <=2 A 1 A D <=4 A E <=12 C F ?? G ?? H ?? C Y 44
- 45. Dijkstra’s Algorithm in action 0 2 2 2 B A 4 C 2 4 D 3 1 E 1 G 11 7 H 2 10 9 3 F 1 4 12 1 Vertex Visited? Cost Found by A Y 0 B Y 2 A C Y 1 A D <=4 A E <=12 C F <=4 B G ?? H ?? 45
- 46. Dijkstra’s Algorithm in action 0 2 2 2 B A 4 C 2 4 D 3 1 E 1 G 11 7 H 2 10 9 3 F 1 4 12 1 Vertex Visited? Cost Found by A Y 0 B Y 2 A C Y 1 A D Y 4 A E <=12 C F <=4 B G ?? H ?? 46
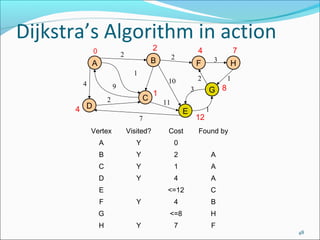
- 47. Dijkstra’s Algorithm in action 0 2 2 2 B A 4 C 2 4 D 3 1 E 1 G 11 7 H 2 10 9 3 F 1 4 7 12 1 Vertex Visited? Cost A Y 0 B Y 2 A C Y 1 A D Y 4 A <=12 C 4 B E F Y G ?? H <=7 Found by F 47
- 48. Dijkstra’s Algorithm in action 0 2 2 2 B A 4 C 2 4 D 2 10 9 11 E H 1 G 8 3 1 7 3 F 1 4 7 12 1 Vertex Visited? Cost A Y 0 B Y 2 A C Y 1 A D Y 4 A <=12 C 4 B <=8 H 7 F E F Y G H Y Found by 48
- 49. Dijkstra’s Algorithm in action 0 2 2 2 B A 4 C 2 4 D 2 10 9 11 E H 1 G 8 3 1 7 3 F 1 4 7 11 1 Vertex Visited? Cost A Y 0 B Y 2 A C Y 1 A D Y 4 A <=11 G E Found by F Y 4 B G Y 8 H H Y 7 F 49
- 50. Dijkstra’s Algorithm in action 0 2 2 2 B A 4 C 2 4 D 2 10 9 11 E H 1 G 8 3 1 7 3 F 1 4 7 11 1 Vertex Visited? Cost Found by A Y 0 B Y 2 A C Y 1 A D Y 4 A E Y 11 G F Y 4 B G Y 8 H H Y 7 F 50
- 51. Time Complexity of Dijskrs Algorithm The efficiency of the Dijskras’s algorithm is analyzed by the iteration of the loop structures. The while loop iteration n – 1 times to visit the minimum weighted edge. Potentially loop must be repeated n times to examine every vertices in the graph. So the time complexity is O(n2).
- 52. QUIZ 1. Find the BREATH-FIRST spanning tree and depth-first spanning tree of the graph GA shown above.
Editor's Notes
- #41: Here’s pseudocode for how dijkstra’s actually works. Speak the algorithm. Notice that we need to be able to find a minimum node and also update costs to nodes.




![Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u ∈ Q
key[u] = ∞;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v ∈ Adj[u]
if (v ∈ Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);](https://image.slidesharecdn.com/graphs-140215035459-phpapp02/85/Graphs-Discrete-structures-Data-Structures-Algorithums-4-320.jpg)
![Prim’s Algorithm
MST-Prim(G, w, r)
6
Q = V[G];
5
for each u ∈ Q
key[u] = ∞;
key[r] = 0;
14
10
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v ∈ Adj[u]
3
if (v ∈ Q and w(u,v) < key[v])
Run
p[v] = u;
key[v] = w(u,v);
4
9
2
15
8
on example graph](https://image.slidesharecdn.com/graphs-140215035459-phpapp02/85/Graphs-Discrete-structures-Data-Structures-Algorithums-5-320.jpg)
![Prim’s Algorithm
MST-Prim(G, w, r)
∞
6
Q = V[G];
5
for each u ∈ Q
∞
key[u] = ∞;
key[r] = 0;
14
10
p[r] = NULL;
while (Q not empty)
∞
u = ExtractMin(Q);
for each v ∈ Adj[u]
3
∞
if (v ∈ Q and w(u,v) < key[v])
Run
p[v] = u;
key[v] = w(u,v);
4
∞
9
∞
2
∞
15
8
on example graph
∞](https://image.slidesharecdn.com/graphs-140215035459-phpapp02/85/Graphs-Discrete-structures-Data-Structures-Algorithums-6-320.jpg)
![Prim’s Algorithm
MST-Prim(G, w, r)
∞
6
Q = V[G];
5
for each u ∈ Q
∞
key[u] = ∞;
key[r] = 0;
14
10
p[r] = NULL;
while (Q not empty)
0
r
u = ExtractMin(Q);
for each v ∈ Adj[u]
3
∞
if (v ∈ Q and w(u,v) < key[v])
Pick
p[v] = u;
key[v] = w(u,v);
4
∞
9
∞
2
∞
8
a start vertex r
15
∞](https://image.slidesharecdn.com/graphs-140215035459-phpapp02/85/Graphs-Discrete-structures-Data-Structures-Algorithums-7-320.jpg)
![Prim’s Algorithm
MST-Prim(G, w, r)
∞
6
4
Q = V[G];
5
for each u ∈ Q
∞
∞
key[u] = ∞;
key[r] = 0;
14
2
10
p[r] = NULL;
while (Q not empty)
0
∞
u
u = ExtractMin(Q);
for each v ∈ Adj[u]
3
8
∞
if (v ∈ Q and w(u,v) < key[v])
Black vertices have been
p[v] = u;
key[v] = w(u,v);
9
15
∞
∞
removed from Q](https://image.slidesharecdn.com/graphs-140215035459-phpapp02/85/Graphs-Discrete-structures-Data-Structures-Algorithums-8-320.jpg)
![Prim’s Algorithm
MST-Prim(G, w, r)
∞
6
4
Q = V[G];
5
for each u ∈ Q
∞
key[u] = ∞;
14
key[r] = 0;
10
p[r] = NULL;
0
u
while (Q not empty)
u = ExtractMin(Q);
3
8
3
for each v ∈ Adj[u]
if (v ∈ Q and w(u,v) < key[v])
p[v] = u;
Black arrows
key[v] = w(u,v);
∞
9
∞
2
∞
15
∞
indicate parent pointers](https://image.slidesharecdn.com/graphs-140215035459-phpapp02/85/Graphs-Discrete-structures-Data-Structures-Algorithums-9-320.jpg)
![Prim’s Algorithm
6
∞
5
MST-Prim(G, w, r)
14
Q = V[G];
for each u ∈ Q
14
10
key[u] = ∞;
key[r] = 0;
0
u
p[r] = NULL;
3
3
while (Q not empty)
u = ExtractMin(Q);
for each v ∈ Adj[u]
if (v ∈ Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
4
∞
9
∞
2
∞
8
15
∞](https://image.slidesharecdn.com/graphs-140215035459-phpapp02/85/Graphs-Discrete-structures-Data-Structures-Algorithums-10-320.jpg)
![Prim’s Algorithm
6
∞
5
MST-Prim(G, w, r)
14
Q = V[G];
for each u ∈ Q
14
10
key[u] = ∞;
key[r] = 0;
0
p[r] = NULL;
3
3
while (Q not empty)
u
u = ExtractMin(Q);
for each v ∈ Adj[u]
if (v ∈ Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
4
∞
9
∞
2
∞
8
15
∞](https://image.slidesharecdn.com/graphs-140215035459-phpapp02/85/Graphs-Discrete-structures-Data-Structures-Algorithums-11-320.jpg)
![Prim’s Algorithm
6
∞
5
MST-Prim(G, w, r)
14
Q = V[G];
for each u ∈ Q
14
10
key[u] = ∞;
key[r] = 0;
0
p[r] = NULL;
3
3
while (Q not empty)
u
u = ExtractMin(Q);
for each v ∈ Adj[u]
if (v ∈ Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
4
∞
9
∞
2
8
8
15
∞](https://image.slidesharecdn.com/graphs-140215035459-phpapp02/85/Graphs-Discrete-structures-Data-Structures-Algorithums-12-320.jpg)
![Prim’s Algorithm
6
∞
5
MST-Prim(G, w, r)
10
Q = V[G];
for each u ∈ Q
14
10
key[u] = ∞;
key[r] = 0;
0
p[r] = NULL;
3
3
while (Q not empty)
u
u = ExtractMin(Q);
for each v ∈ Adj[u]
if (v ∈ Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
4
∞
9
∞
2
8
8
15
∞](https://image.slidesharecdn.com/graphs-140215035459-phpapp02/85/Graphs-Discrete-structures-Data-Structures-Algorithums-13-320.jpg)
![Prim’s Algorithm
6
∞
5
MST-Prim(G, w, r)
10
Q = V[G];
for each u ∈ Q
14
10
key[u] = ∞;
key[r] = 0;
0
p[r] = NULL;
3
3
while (Q not empty)
u = ExtractMin(Q);
for each v ∈ Adj[u]
if (v ∈ Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
4
∞
9
∞
2
8
8
u
15
∞](https://image.slidesharecdn.com/graphs-140215035459-phpapp02/85/Graphs-Discrete-structures-Data-Structures-Algorithums-14-320.jpg)
![Prim’s Algorithm
6
∞
5
MST-Prim(G, w, r)
10
Q = V[G];
for each u ∈ Q
14
10
key[u] = ∞;
key[r] = 0;
0
p[r] = NULL;
3
3
while (Q not empty)
u = ExtractMin(Q);
for each v ∈ Adj[u]
if (v ∈ Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
4
9
2
∞
2
8
8
u
15
∞](https://image.slidesharecdn.com/graphs-140215035459-phpapp02/85/Graphs-Discrete-structures-Data-Structures-Algorithums-15-320.jpg)
![Prim’s Algorithm
6
∞
5
MST-Prim(G, w, r)
10
Q = V[G];
for each u ∈ Q
14
10
key[u] = ∞;
key[r] = 0;
0
p[r] = NULL;
3
3
while (Q not empty)
u = ExtractMin(Q);
for each v ∈ Adj[u]
if (v ∈ Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
4
9
2
∞
2
8
8
u
15
15](https://image.slidesharecdn.com/graphs-140215035459-phpapp02/85/Graphs-Discrete-structures-Data-Structures-Algorithums-16-320.jpg)
![Prim’s Algorithm
6
∞
5
MST-Prim(G, w, r)
10
Q = V[G];
for each u ∈ Q
14
10
key[u] = ∞;
key[r] = 0;
0
p[r] = NULL;
3
3
while (Q not empty)
u = ExtractMin(Q);
for each v ∈ Adj[u]
if (v ∈ Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
u
4
9
2
∞
2
8
8
15
15](https://image.slidesharecdn.com/graphs-140215035459-phpapp02/85/Graphs-Discrete-structures-Data-Structures-Algorithums-17-320.jpg)
![Prim’s Algorithm
6
4
5
MST-Prim(G, w, r)
10
Q = V[G];
for each u ∈ Q
14
10
key[u] = ∞;
key[r] = 0;
0
p[r] = NULL;
3
3
while (Q not empty)
u = ExtractMin(Q);
for each v ∈ Adj[u]
if (v ∈ Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
u
4
9
2
∞
2
8
8
15
15](https://image.slidesharecdn.com/graphs-140215035459-phpapp02/85/Graphs-Discrete-structures-Data-Structures-Algorithums-18-320.jpg)
![Prim’s Algorithm
6
4
5
MST-Prim(G, w, r)
5
Q = V[G];
for each u ∈ Q
14
10
key[u] = ∞;
key[r] = 0;
0
p[r] = NULL;
3
3
while (Q not empty)
u = ExtractMin(Q);
for each v ∈ Adj[u]
if (v ∈ Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
u
4
9
2
∞
2
8
8
15
15](https://image.slidesharecdn.com/graphs-140215035459-phpapp02/85/Graphs-Discrete-structures-Data-Structures-Algorithums-19-320.jpg)
![Prim’s Algorithm
6
4
5
MST-Prim(G, w, r)
5
Q = V[G];
for each u ∈ Q
14
10
key[u] = ∞;
key[r] = 0;
0
p[r] = NULL;
3
3
while (Q not empty)
u = ExtractMin(Q);
for each v ∈ Adj[u]
if (v ∈ Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
u
4
9
2
9
2
8
8
15
15](https://image.slidesharecdn.com/graphs-140215035459-phpapp02/85/Graphs-Discrete-structures-Data-Structures-Algorithums-20-320.jpg)
![Prim’s Algorithm
6
4
5
MST-Prim(G, w, r)
5
Q = V[G];
for each u ∈ Q
14
10
key[u] = ∞;
key[r] = 0;
0
p[r] = NULL;
3
3
while (Q not empty)
u = ExtractMin(Q);
for each v ∈ Adj[u]
if (v ∈ Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
4
u
9
2
9
2
8
8
15
15](https://image.slidesharecdn.com/graphs-140215035459-phpapp02/85/Graphs-Discrete-structures-Data-Structures-Algorithums-21-320.jpg)
![Prim’s Algorithm
u
6
4
5
MST-Prim(G, w, r)
5
Q = V[G];
for each u ∈ Q
14
10
key[u] = ∞;
key[r] = 0;
0
p[r] = NULL;
3
3
while (Q not empty)
u = ExtractMin(Q);
for each v ∈ Adj[u]
if (v ∈ Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
4
9
2
9
2
8
8
15
15](https://image.slidesharecdn.com/graphs-140215035459-phpapp02/85/Graphs-Discrete-structures-Data-Structures-Algorithums-22-320.jpg)
![Prim’s Algorithm
6
4
5
MST-Prim(G, w, r)
5
Q = V[G];
for each u ∈ Q
14
10
key[u] = ∞;
key[r] = 0;
0
p[r] = NULL;
3
3
while (Q not empty)
u = ExtractMin(Q);
for each v ∈ Adj[u]
if (v ∈ Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
u
4
9
2
9
2
8
8
15
15](https://image.slidesharecdn.com/graphs-140215035459-phpapp02/85/Graphs-Discrete-structures-Data-Structures-Algorithums-23-320.jpg)
![Prim’s Algorithm
6
4
5
MST-Prim(G, w, r)
5
Q = V[G];
for each u ∈ Q
14
10
key[u] = ∞;
key[r] = 0;
0
p[r] = NULL;
3
3
while (Q not empty)
u = ExtractMin(Q);
for each v ∈ Adj[u]
if (v ∈ Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
4
9
2
u
2
8
8
9
15
15](https://image.slidesharecdn.com/graphs-140215035459-phpapp02/85/Graphs-Discrete-structures-Data-Structures-Algorithums-24-320.jpg)
![Review: Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u ∈ Q
key[u] = ∞;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v ∈ Adj[u]
if (v ∈ Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);](https://image.slidesharecdn.com/graphs-140215035459-phpapp02/85/Graphs-Discrete-structures-Data-Structures-Algorithums-25-320.jpg)
![Dijkstra’s Algorithm
Similar to (BFS) Breadth-First Search
Grow a tree gradually, advancing from vertices taken from a
queue
Also similar to Prim’s algorithm for MST
Use a priority queue keyed on d[v]](https://image.slidesharecdn.com/graphs-140215035459-phpapp02/85/Graphs-Discrete-structures-Data-Structures-Algorithums-26-320.jpg)