Introduction to the cryptography behind blockchain (from roots to quantum crypto)
1 like359 views
The document provides an introduction to cryptography concepts behind blockchain, beginning with symmetric key cryptography like the Data Encryption Standard (DES) developed by Horst Feistel at IBM in the 1970s. It then discusses the development of public key cryptography by Whitfield Diffie, Martin Hellman, Ronald Rivest, Adi Shamir, and Leonard Adleman in the 1970s, which introduced digital signatures and solved the key distribution problem. The document continues discussing the use of hash functions, elliptic curve cryptography, and computational proof-of-work concepts that are fundamental to blockchain technology.
Introduction to the cryptography behind blockchain (from roots to quantum crypto)
- 1. Marcelo Sávio IBM Industry Solutions Architect https://www.linkedin.com/in/msavio/ Introduction to the Cryptography Behind Blockchain (from roots to Quantum)
- 2. The Problem… … inefficient, expensive, vulnerable Insurer records Auditor records Regulator records Participant A’s records Bank records Participant B’s records
- 3. … with consensus, provenance, immutability and finality Auditor records Regulator records Bank records Participant B’s records Blockchain Insurer records Participant A’s records The Solution: A shared, replicated, permissioned ledger …
- 4. 4 Blockchain is a technology platform that creates a distributed ledger between participants to allow transfer of asset ownership or transactions using “smart contracts” in a secured and permissioned environment guaranteed by cryptographic techniques and algorithms. Append-only distributed system of record shared across business network Ensuring secure, authenticated & verifiable transactions Business terms embedded in transaction database & executed with transactions Shared Ledger Smart Contract Cryptography Consistent SecureSimple Efficient Transparent Blockchain networks are . . . Consensus All parties agree to network verified transaction How does it work?
- 5. 5 All the cryptographic techniques and algorithms used in Blockchain have been around for quite a long time, being used on the Internet (e-commerce, e-banking and many other applications), cell phones etc. Ensuring secure, authenticated & verifiable transactions Cryptography Where else does Blockchain cryptography work?
- 8. 8 BITCOIN (Crypto Currency) BLOCKCHAIN (Electronic Ledger) Other Crypto Currencies
- 9. 9 BITCOIN (Crypto Currency) BLOCKCHAIN (Electronic Ledger) Other Crypto Currencies Cryptography Computational Proof of Work Peer to Peer Networks
- 10. 10 Claude Shannon Symmetric Key Cryptography BITCOIN (Crypto Currency) DES Key Exchange Problem Elliptic Curve CryptographyCryptography Hash Horst Feistel ACM article Asymmetric Key Cryptography CHQ RSA Computational Proof of Work Peer to Peer Networks BLOCKCHAIN (Electronic Ledger) Hashing Algorithms Many consensus Algorithms Trade Anything Other Crypto Currencies Enterprise Applications MIT Digital Signature
- 11. 11 Claude Shannon Symmetric Key Cryptography BITCOIN (Crypto Currency) DES Key Exchange Problem Elliptic Curve CryptographyCryptography Hash Horst Feistel ACM article Asymmetric Key Cryptography CHQ RSA Computational Proof of Work Peer to Peer Networks BLOCKCHAIN (Electronic Ledger) Hashing Algorithms Many consensus Algorithms Trade Anything Other Crypto Currencies Enterprise Applications MIT Digital Signature Quantum Computing Quantum Cryptography
- 13. 13 Ancient Egypt Ancient Mesopotamia Ancient Greece Middle Ages I am NOT going to talk about this…
- 14. Enigma Alan Turing (1912-1954) Bletchley Park, UK Nor this…
- 15. 15 But you definitely should learn about this fascinating history. And for that I recommend these two books: – The Codebreakers by David Kahn, 1996, Scribner – The Code Book: The Science of Secrecy from Ancient Egypt to Quantum Cryptography, by Simon Singh, 1999, Anchor Books (Available in Brazilian Portuguese)
- 16. 16 Claude Elwood Shannon (1916 - 2001) In Oct 1949, published another paper entitled "Communication Theory of Secrecy Systems“, which is generally credited with transforming cryptography from an art to a science. Actually this paper was a shorter and declassified version of a previous paper Shannon published in Sep 1945 in a Confidential Classified report entitled “A Mathematical Theory of Cryptography”. Shannon developed the information theory concepts in support of cryptography. Our talk today starts in the middle of the last Century… Joined AT&T Bell Telephones (New Jersey, USA) in 1941 as a research mathematician and remained there until 1972. Published "A Mathematical Theory of Communication“ in 1948 which founded the Information Theory.
- 17. Horst Feistel (1915 - 1990) Was a German-born cryptographer who immigrated to the US and in 1968 joined IBM T.J. Watson Research Center in Yorktown Heights, NY. There he led a lab which was the only significant non- governmental cryptographic research group in the US (and probably in the world) at the time. IBM filed several patents based on his cryptographic ideas built on top of Claude Shannon’s concepts (confusion, diffusion etc.) He joined IBM in a very propitious moment, just in time to solve the problem of security of electronic transactions on Automated Teller Machines for the Lloyds bank cashpoint system. Cryptography was an almost exclusively military matter, until…
- 18. Feistel developed in the APL Programming Language a block cipher cryptographic system called LUCIFER to protect the data for the remote cash-dispensing system. This not only represented a new paradigm for encryption systems but also mainly brought encryption from a little-known military science into our daily lives, and stimulated research in cryptography and competition in creating encryption algorithms. The LUCIFER algorithm was then submitted by IBM to the US National Bureau of Standards (NBS) following the agency's invitation to propose a candidate for the protection of government data. In January 1977 it was published as an official Federal Information Processing Standard (FIPS) for the United States, in which it became known as Data Encryption Standard (DES) and became widely used – and not only by the US Government - for almost 40 years. “Almost all of the encryption algorithms ... can trace their roots back to DES.” Bruce Schneier, Information Security Expert https://www.schneier.com/
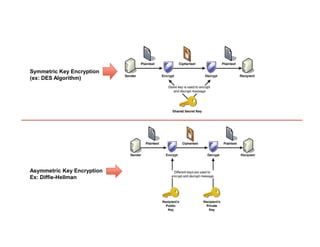
- 19. • The Data Encryption Standard (DES) uses a Symmetric Encryption technique, in which the same key is applied at both sides (sender/receiver), known as the “Secret Key” • It that takes a fixed-length string of plaintext bits and transforms it through a series of complicated operations into another ciphertext bitstring of the same length. • The secret key consists of 64 bits; however, only 56 of these are actually used by the encryption algorithm, since 8 bits are used solely for checking parity. • DES was substituted only after 2001 with the advent of the AES (Advanced Encryption Standard) algorithm, which is based on the Rijndael developed by two Belgian cryptographers (Vincent Rijmen and Joan Daemen), who submitted a proposal to the US NIST during the AES selection process. • Other famous symmetric encryption algorithms are: Triple- DES, CDMF (Commercial Data Masking Facility), IDEA (International Data Encryption Algorithm), RC2, RC4, RC5, RC6, MARS, Blowfish and Twofish. Secret Key 1 Secret Key 1 E N C R Y P T D E C R Y P T =
- 20. It was the very first general-public information about Cryptography and Privacy. Feistel also published a seminal article on Scientific American, in 1973.
- 21. After Feistel’s work on LUCIFER and his article on Scientific American, many researchers became interested in the field of Cryptography. and some of them decided to investigate on how to solve a fundamental problem: how to send the symmetric key to the other side through a non-trusted channel ?
- 22. Martin Hellman In late 1968 began work with AI at IBM’s TJ Watson Research Center where he met members of the IBM cryptographic research program, including Horst Feistel and Alan G. Konheim, another IBM cryptographer. “I remember many conversations with Feistel. That year at IBM and my interactions with Horst played a major role in my later moving into cryptography.” Once he had lunch with Feistel, who talked not only about classical cryptographic systems as well as about the “problems that sounded unsolvable but could actually be solved”, as Feistel said. So Hellman decided solve the Key Exchange Problem. He left IBM and went to the MIT and then to the Electrical Engineering Faculty at Stanford University.
- 23. Whitfield Diffie Mathematician from the Stanford University who started to study cryptography. In the summer of 1974 Whitfield Diffie went to the IBM and spoke to Alan Konheim about challenges in the Cryptography field. Konheim was a little secretive but told him one very important thing: “An old friend of mine, named Martin Hellman, worked here until some time ago, and now he's out at Stanford. And two people can work on a problem much better than one, and so when you get back to Stanford, you should look him up.” In late 1974, at the suggestion of Konheim, Diffie visited Hellman in Stanford. A planned half-hour early afternoon meeting between Diffie and Hellman evolved to an afternoon-long discussion followed by dinner and further exchange well into the evening. And it was just the beginning… In Hellman’s words, “it was a mild epiphany, finding an intellectual soul mate.” Alan Konheim, IBM
- 24. Diffie and Hellman, 1976 The first public idea of an asymmetric public-private key cryptosystem “We stand today on the brink of a revolution in cryptography.”“We stand today on the brink of a revolution in cryptography.”
- 25. Symmetric Key Encryption (ex: DES Algorithm) Asymmetric Key Encryption Ex: Diffie-Hellman
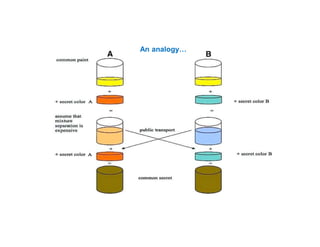
- 26. An analogy…
- 27. Public-key cryptography depends upon the existence of mathematical functions that are easy to compute whereas their inverse function is relatively difficult to do. Example: Exponentiation vs. logarithms Suppose you take the number 3 to the 6th power; again, it is relatively easy to calculate 36 = 729. But if you start with the number 729 and need to determine the two integers, x and y so that logx729 = y, it will take longer to find the two values.
- 29. Ron Rivest, Adi Shamir, and Leonard Adleman from the Massachusetts Institute of Technology (MIT) They invented (and patented) the RSA Algorithm which was the first public-key cryptosystems implemented and widely used for secure data transmission. In RSA, this asymmetry is based on the practical difficulty of the factorization of the product of two large prime numbers, the "factoring problem". The dawn of the implementable Public-Key Cryptography, 1977 • They filed the original RSA Patent with the US Patent Office on Dec 14, 1977, U.S. Patent 4,405,829 . • They founded RSA Data Security in 1982. • In 1996 Security Dynamics acquired RSA Data Security but kept the name (RSA Security). • In 1997 RSA Security proposed the first of the DES Challenges which led to the first public breaking of DES. • In 2006 EMC acquired RSA Security. • In 2016 Dell merged with EMC and RSA Security became a subsidiary of Dell Technologies • On Sept 2020 Symphony Technology Group (STG) acquired RSA Security from Dell Technologies
- 30. RSA explanation (tried to make it easy) Bob Private Key = 11,13 Bob Public Key = 143 Bob Public Key (143) Bob Private Key (11, 13) ☺ Alice Encrypts message to Bob using Bob’s Public Key (143) ☺ Bob Decrypts message from Alice using its own Private Key (11,13) ☺ H Hacker will know the message was encrypted with B’s Public Key (143) and will have to factor this number to find the two prime numbers that were multiplied to generate it Suppose you have two prime numbers, 11 and 13, and you need to calculate the product; it should take almost no time to calculate that value, which is 143. Now suppose, instead, that you have a number that is a product of two primes, 143, and you need to determine those prime factors. You will eventually come up with the solution but whereas calculating the product took milliseconds, factoring will take much longer. That’s it.
- 31. Public Key Private Key Reality is about random BIG prime numbers (example) = This RSA-768 public key above, which has 232 decimal digits (768 bits), was factored in a test in 2009 over the span of two years, by a group of 15 people using a collection of parallel computers amounted approximately to the equivalent of almost 2000 years of computing time on a single-core 2.2 GHz AMD Opteron-based computer.
- 33. The (secret) work done in the UK For some time, it was a quiet secret that a team at the UK's Government Communications Headquarters (GCHQ) had first developed Public Key Cryptography in the early 1970s. Because of the nature of the work, GCHQ kept the original memos classified. In the 90s, however, the GCHQ changed their posture when they realized that there was nothing to gain by continued silence. Documents show that a GCHQ mathematician named James Ellis started research into the key distribution problem in 1969 and that by 1975, James Ellis, Clifford Cocks, and Malcolm Williamson had worked out all of the fundamental details of PKC, yet couldn't talk about their work. By 1999, Ellis, Cocks, and Williamson began to get their due credit in a break-through article in WIRED Magazine (https://www.wired.com/1999/04/crypto/) James Ellis Clifford Cocks Malcolm Williamson
- 34. ☺ Alice ☺ Bob ☺Alice ☺Alice The other way around of using Public/Private Keys: Digital Signature
- 35. Primality test using Elliptic Curve, 1985 A primality test is an algorithm for determining whether an input number is prime, which is important to key generation, that’s why among other fields of mathematics, it is used for cryptography. Unlike integer factorization, primality tests do not generally give prime factors, only stating whether the input number is prime or not. H. W. Lenstra developed the concept of using elliptic curves in factorization in 1985, and the implications for its use in primality testing (and proving) followed quickly. Hendrik Lenstra University of Amsterdam
- 36. Inspired by the work of Lenstra, Elliptic-Curve Cryptography (ECC) was developed as an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite numeric fields. It proposed independently by Neal Koblitz (UW) and Victor Miller (IBM), in 1985. Elliptic curve cryptography algorithms entered wide use after 2005. It requires smaller keys compared to RSA to provide equivalent security. Elliptic-Curve Cryptography (ECC), 1985 Neal Koblitz Univ. Washington Victor Miller IBM
- 37. The cryptographic hash mathematical algorithm that maps data of arbitrary size to a bit string of a fixed size (a hash) and is designed to be a one-way function, that is, a function which is infeasible to invert. Cryptographic Hash 1979 Ralph Merkle Stanford University
- 38. Merkle Tree, 1979 Example of Crypto Hash Algorithms: MD5, RIPEMD-160, SHA-256, etc.
- 39. In 1992 email spam messaging was already a problem. Two researchers Cynthia Dwork (IBM) and Moni Naor (Weizmann IS), tried to solve it. The essay, “Pricing via Processing or Combatting Junk Mail,” presented a way to prevent spammers from sending out unsolicited mass messages. Computational Proof of Work (1990s) In 1997, a member of the cypherpunk movement named Adam Back founded a protocol called HashCash. Many of the ideas presented with the HashCash protocol evolved into what we understand to be a Proof of Work mechanism today, including something called “Double Spending Protection,” a foundational concept in blockchain. In 1999 Markus Jakobsson (USCD) and Ari Juels (RSA) wrote a paper called “Proof of Work and Bread Pudding Protocols,” thus coining the term , defined as a protocol in which a prover demonstrates to a verifier that has expended a certain level of computational effort in a specified interval of time. Markus Jakobsson Ari Juels Adam Back
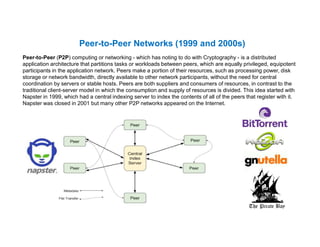
- 40. Peer-to-Peer Networks (1999 and 2000s) Peer-to-Peer (P2P) computing or networking - which has noting to do with Cryptography - is a distributed application architecture that partitions tasks or workloads between peers, which are equally privileged, equipotent participants in the application network. Peers make a portion of their resources, such as processing power, disk storage or network bandwidth, directly available to other network participants, without the need for central coordination by servers or stable hosts. Peers are both suppliers and consumers of resources, in contrast to the traditional client-server model in which the consumption and supply of resources is divided. This idea started with Napster in 1999, which had a central indexing server to index the contents of all of the peers that register with it. Napster was closed in 2001 but many other P2P networks appeared on the Internet.
- 41. The paper detailed methods of using a peer-to-peer network to generate what was described as "a system for electronic transactions without relying on trust". • The Internet domain name "bitcoin.org" was registered on 18 August 2008. • On 31 October 2008, a link to a paper authored by Satoshi Nakamoto titled Bitcoin: A Peer-to-Peer Electronic Cash System was posted to a cryptography mailing list. • Nakamoto implemented the bitcoin software as open-source code and released it in January 2009. • Nakamoto's identity remains unknown. The birth of Bitcoin, 2008 Satoshi created great innovation combining quite old things: Cryptography (Public-Private keys/Elliptic Curve Cryptography, Digital Signatures, Hash & Merkle Trees), from the 70s/80s, Proof of Work (90s) and P2P Networks from 90s and 2000s
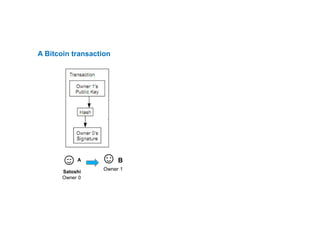
- 42. A Bitcoin transaction A Satoshi Owner 0 ☺B Owner 1
- 43. A Chain of Transactions Blocks Blockchain . . . Owner 0 ☺ Owner 1 ☺ Owner 2 ☺ Owner 3 ☺ Owner 1 ☺ Owner 2
- 45. Some examples of consensus algorithms Proof of stake Proof of Elapsed Time PBFT (Byzantine fault tolerance)based Proof of work Kafka / Zookeeper Solo / No-ops
- 46. Consensus algorithms have different strengths and weaknesses Require validators to solve difficult cryptographic puzzles PROs: Works in untrusted networks CONS: Relies on energy use; slow to confirm transactions Example usage: Bitcoin, Ethereum Require validators to hold currency in escrow PROs: Works in untrusted networks CONS: Requires intrinsic (crypto)currency, ”Nothing at stake” problem Example usage: Nxt Wait time in a trusted execution environment randomizes block generation PROs: Efficient CONS: Requires processor extensions Example usage: Hyperledger Sawtooth Proof of stake Proof of Elapsed Time Proof of work
- 47. Validators apply received transactions without consensus PROs: Very quick; suited to development CONS: No consensus; can lead to divergent chains Example usage: Hyperledger Fabric V1 Practical Byzantine Fault Tolerance implementations PROs: Reasonably efficient and tolerant against malicious peers CONS: Validators are known and totally connected Example usage: Hyperledger Fabric V0.6 Ordering service distributes blocks to peers PROs: Efficient and fault tolerant CONS: Does not guard against malicious activity Example usage: Hyperledger Fabric V1 PBFT-based Solo / No-ops Kafka / Zookeeper Consensus algorithms have different strengths and weaknesses
- 48. A Blockchain for Business Reference (Don Tapscott) http://blockchain-revolution.com/ https://www.blockchainresearchinstitute.org/
- 49. A Technical Reference for Blockchain • Links to Videos, Slides, etc. http://bit.ly/CMbcDB • Telegram, Twitter, Instagram: @seemohan • Facebook: http://www.facebook.com/cmohan • LinkedIn: http://www.linkedin.com/in/seemohan/ Distinguished Visiting Professor, Tsinghua University, Beijing Advisor, Kerala Blockchain Academy & Tamil Nadu e-Governance Agency, India Retired IBM Fellow (1997-2020), IBM Research (1981-2020), San Jose, USA.
- 50. …but what about quantum computers breaking the existing cryptographic systems?
- 52. The Shor Algorithm (1994) Created by the mathematician Peter Shor (now MIT) while he was working for AT&T Research Labs. It is an algorithm that runs on a quantum computer for solving the integer factorization problem: given an integer N, find its prime factors. Yes, RSA can be broken with Quantum Computers
- 53. The Shor Algorithm for ECC (2003) Yes, ECC can be broken with Quantum Computers
- 54. But there is also Quantum Cryptography Quantum key distribution (QKD) is a secure communication method which implements a cryptographic protocol involving components of quantum mechanics. It enables two parties to produce a shared random secret key known only to them, which can then be used to encrypt and decrypt messages. It is often called quantum cryptography. BB84 was the first QKD scheme developed by Charles Bennett (IBM) and Gilles Brassard (Université de Montréal) in 1984. There are others schemas. Charles Bennett IBM Gilles Brassard Université de Montréal
- 55. The Future? Lattice Cryptography and Fully Homomorphic Encryption (FHE). • IBM researchers are developing a new security method built on an underlying architecture known as lattice cryptography, which hides data inside complex math problems (algebraic structures) called lattices. The difficulty in solving these math problems is useful for cryptographers, because they can apply this intractability to protect information. • Unlike commonly-used cryptosystems like RSA and ECC, lattice-based cryptosystems cannot feasibly (as far as we know) be broken by quantum computers. The NSA cited this as a reason to begin transitioning to lattice-based cryptosystems, or to other "post-quantum" cryptosystems. • Lattice-based cryptography the basis of another encryption technology called Fully Homomorphic Encryption (FHE) – see next slide. https://www.research.ibm.com/5-in-5/lattice-cryptography/
- 56. The Future? Lattice Cryptography and Fully Homomorphic Encryption (FHE). • Homomorphic encryption is a form of encryption that allows computation on ciphertexts, generating an encrypted result which, when decrypted, matches the result of the operations as if they had been performed on the plaintext. Craig Gentry IBM • In 2009, Craig Gentry constructed the first Fully Homomorphic Encryption (FHE) scheme, which allows data to be processed in arbitrarily complex ways while it remains encrypted, solving a major open problem that had been unsolved for 30 years. • FHE allows data processing to be outsourced (e.g., to the cloud) without sacrificing privacy - in particular, without disclosing the decryption key.