![Example 5.6
5.1.2 Continued
Design an 8 × 8 permutation table for a straight P-box that
moves the two middle bits (bits 4 and 5) in the input word to
the two ends (bits 1 and 8) in the output words. Relative
positions of other bits should not be changed.
Solution
We need a straight P-box with the table [4 1 2 3 6 7 8 5].
The relative positions of input bits 1, 2, 3, 6, 7, and 8 have not
been changed, but the first output takes the fourth input and
the eighth output takes the fifth input.](https://image.slidesharecdn.com/introductiontomodernsymmetric-keyciphers-220321133119/85/Introduction-to-modern_symmetric-key_ciphers-10-320.jpg)
Introduction to modern_symmetric-key_ciphers
- 1. Course name :Crytography Course Code :18UCAE64 PART III :Elective Credits :04 Programme :Computer Applications Course Instructor :R.Vasuki,M.C.A.,M.Phil,NET, Assistant Professor, Dept of Computer Science 1.1
- 2. 5.2
- 3. Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Chapter 5 Introduction to Modern Symmetric-key Ciphers
- 4. 5-1 MODERN BLOCK CIPHERS A symmetric-key modern block cipher encrypts an n-bit block of plaintext or decrypts an n-bit block of ciphertext. The encryption or decryption algorithm uses a k-bit key. 5.1.1 Substitution or Transposition 5.1.2 Block Ciphers as Permutation Groups 5.1.3 Components of a Modern Block Cipher 5.1.4 Product Ciphers 5.1.5 Two Classes of Product Ciphers 5.1.6 Attacks on Block Ciphers Topics discussed in this section:
- 5. Figure 5.1 A modern block cipher 5.1 Continued
- 6. Modern block ciphers normally are keyed substitution ciphers in which the key allows only partial mappings from the possible inputs to the possible outputs. 5.1.3 Components of a Modern Block Cipher A P-box (permutation box) parallels the traditional transposition cipher for characters. It transposes bits. P-Boxes
- 7. Figure 5.4 Three types of P-boxes 5.1.3 Continued
- 8. Example 5.5 5.1.3 Continued Figure 5.5 The possible mappings of a 3 × 3 P-box Figure 5.5 shows all 6 possible mappings of a 3 × 3 P-box.
- 9. 5.1.3 Continued Table 5.1 Example of a permutation table for a straight P-box Straight P-Boxes
- 10. Example 5.6 5.1.2 Continued Design an 8 × 8 permutation table for a straight P-box that moves the two middle bits (bits 4 and 5) in the input word to the two ends (bits 1 and 8) in the output words. Relative positions of other bits should not be changed. Solution We need a straight P-box with the table [4 1 2 3 6 7 8 5]. The relative positions of input bits 1, 2, 3, 6, 7, and 8 have not been changed, but the first output takes the fourth input and the eighth output takes the fifth input.
- 11. Compression P-Boxes 5.1.3 Continued A compression P-box is a P-box with n inputs and m outputs where m < n. Table 5.2 Example of a 32 × 24 permutation table
- 12. 5.1.3 Continued Table 5.2 Example of a 32 × 24 permutation table Compression P-Box
- 13. Expansion P-Boxes 5.1.3 Continued An expansion P-box is a P-box with n inputs and m outputs where m > n. Table 5.3 Example of a 12 × 16 permutation table
- 14. 5.1.3 Continued P-Boxes: Invertibility A straight P-box is invertible, but compression and expansion P-boxes are not. Note
- 15. Example 5.7 5.1.3 Continued Figure 5.6 shows how to invert a permutation table represented as a one-dimensional table. Figure 5.6 Inverting a permutation table
- 16. Figure 5.7 Compression and expansion P-boxes are non-invertible 5.1.3 Continued
- 17. 5.1.3 Continued S-Box An S-box (substitution box) can be thought of as a miniature substitution cipher. An S-box is an m × n substitution unit, where m and n are not necessarily the same. Note
- 18. Example 5.8 5.1.3 Continued In an S-box with three inputs and two outputs, we have The S-box is linear because a1,1 = a1,2 = a1,3 = a2,1 = 1 and a2,2 = a2,3 = 0. The relationship can be represented by matrices, as shown below:
- 19. Example 5.9 5.1.3 Continued In an S-box with three inputs and two outputs, we have where multiplication and addition is in GF(2). The S-box is nonlinear because there is no linear relationship between the inputs and the outputs.
- 20. Example 5.10 5.1.3 Continued The following table defines the input/output relationship for an S-box of size 3 × 2. The leftmost bit of the input defines the row; the two rightmost bits of the input define the column. The two output bits are values on the cross section of the selected row and column. Based on the table, an input of 010 yields the output 01. An input of 101 yields the output of 00.
- 21. Example 5.11 5.1.3 Continued Figure 5.8 shows an example of an invertible S-box. For example, if the input to the left box is 001, the output is 101. The input 101 in the right table creates the output 001, which shows that the two tables are inverses of each other. Figure 5.8 S-box tables for Example 5.11
- 22. 5.1.3 Continued Exclusive-Or An important component in most block ciphers is the exclusive-or operation. Figure 5.9 Invertibility of the exclusive-or operation
- 23. 5.1.3 Continued Exclusive-Or (Continued) An important component in most block ciphers is the exclusive-or operation. As we discussed in Chapter 4, addition and subtraction operations in the GF(2n) field are performed by a single operation called the exclusive- or (XOR). The five properties of the exclusive-or operation in the GF(2n) field makes this operation a very interesting component for use in a block cipher: closure, associativity, commutativity, existence of identity, and existence of inverse.
- 24. Figure 5.9 Invertibility of the exclusive-or operation 5.1.1 Continued
- 25. 5.1.3 Continued Circular Shift Another component found in some modern block ciphers is the circular shift operation. Figure 5.10 Circular shifting an 8-bit word to the left or right
- 26. 5.1.3 Continued Swap The swap operation is a special case of the circular shift operation where k = n/2. Figure 5.11 Swap operation on an 8-bit word
- 27. 5.1.3 Continued Split and Combine Two other operations found in some block ciphers are split and combine. Figure 5.12 Split and combine operations on an 8-bit word
- 28. Figure 5.12 Split and combine operations on an 8-bit word 5.1.3 Continued
- 29. Shannon introduced the concept of a product cipher. A product cipher is a complex cipher combining substitution, permutation, and other components discussed in previous sections. 5.1.4 Product Ciphers
- 30. Diffusion The idea of diffusion is to hide the relationship between the ciphertext and the plaintext. 5.1.4 Continued Diffusion hides the relationship between the ciphertext and the plaintext. Note
- 31. Confusion The idea of confusion is to hide the relationship between the ciphertext and the key. 5.1.4 Continued Confusion hides the relationship between the ciphertext and the key. Note
- 32. Rounds Diffusion and confusion can be achieved using iterated product ciphers where each iteration is a combination of S-boxes, P-boxes, and other components. 5.1.4 Continued
- 33. Figure 5.13 A product cipher made of two rounds 5.1.4 Continued
- 34. Figure 5.14 Diffusion and confusion in a block cipher 5.1.4 Continued
- 35. Modern block ciphers are all product ciphers, but they are divided into two classes. 1. Feistel ciphers 2. Non-Feistel ciphers 5.1.5 Two Classes of Product Ciphers
- 36. Feistel Ciphers Feistel designed a very intelligent and interesting cipher that has been used for decades. A Feistel cipher can have three types of components: self-invertible, invertible, and noninvertible. 5.1.5 Continued
- 37. Figure 5.15 The first thought in Feistel cipher design 5.1.5 Continued Diffusion hides the relationship between the ciphertext and the plaintext. Note
- 38. Figure 5.16 Improvement of the previous Feistel design 5.1.5 Continued
- 39. Figure 5.17 Final design of a Feistel cipher with two rounds 5.1.5 Continued
- 40. Non-Feistel Ciphers A non-Feistel cipher uses only invertible components. A component in the encryption cipher has the corresponding component in the decryption cipher. 5.1.5 Continued
- 41. Attacks on traditional ciphers can also be used on modern block ciphers, but today’s block ciphers resist most of the attacks discussed in Chapter 3. 5.1.6 Attacks on Block Ciphers
- 42. Differential Cryptanalysis Eli Biham and Adi Shamir introduced the idea of differential cryptanalysis. This is a chosen-plaintext attack. 5.1.5 Continued
- 43. Example 5.14 5.1.6 Continued We add one S-box to Example 5.13, as shown in Figure 5.19. Figure 5.19 Diagram for Example 5.14
- 44. Example 5.14 Continued 5.1.6 Continued Eve now can create a probabilistic relationship as shone in Table 5.4. Table 5.4 Differential input/output
- 45. Example 5.15 5.1.6 Continued The heuristic result of Example 5.14 can create probabilistic information for Eve as shown in Table 5.5. Table 5.5 Differential distribution table
- 46. 5.1.6 Continued A more detailed differential cryptanalysis is given in Appendix N. Note Differential cryptanalysis is based on a nonuniform differential distribution table of the S-boxes in a block cipher. Note
- 47. Linear Cryptanalysis Linear cryptanalysis was presented by Mitsuru Matsui in 1993. The analysis uses known plaintext attacks. 5.1.6 Continued
- 48. Figure 5.20 A simple cipher with a linear S-box 5.1.6 Continued
- 49. 5.1.6 Continued Solving for three unknowns, we get. This means that three known-plaintext attacks can find the values of k0, k1, and k2 .
- 50. 5-2 MODERN STREAM CIPHERS In a modern stream cipher, encryption and decryption are done r bits at a time. We have a plaintext bit stream P = pn…p2 p1, a ciphertext bit stream C = cn…c2 c1, and a key bit stream K = kn…k2 k1, in which pi , ci , and ki are r-bit words. 5.2.1 Synchronous Stream Ciphers 5.2.2 Nonsynchronous Stream Ciphers Topics discussed in this section:
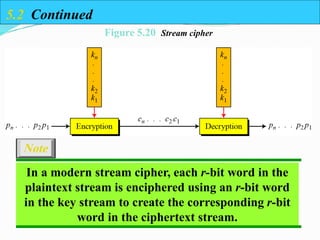
- 51. 5.2 Continued In a modern stream cipher, each r-bit word in the plaintext stream is enciphered using an r-bit word in the key stream to create the corresponding r-bit word in the ciphertext stream. Note Figure 5.20 Stream cipher
- 52. 5.2.1 Synchronous Stream Ciphers In a synchronous stream cipher the key is independent of the plaintext or ciphertext. Note Figure 5.22 One-time pad
- 53. Example 5.17 5.2.1 Continued What is the pattern in the ciphertext of a one-time pad cipher in each of the following cases? a. The plaintext is made of n 0’s. b. The plaintext is made of n 1’s. c. The plaintext is made of alternating 0’s and 1’s. d. The plaintext is a random string of bits. Solution a. Because 0 ki = ki , the ciphertext stream is the same as the key stream. If the key stream is random, the ciphertext is also random. The patterns in the plaintext are not preserved in the ciphertext.
- 54. Example 5.7 5.2.1 Continued b. Because 1 ki = ki where ki is the complement of ki , the ciphertext stream is the complement of the key stream. If the key stream is random, the ciphertext is also random. Again the patterns in the plaintext are not preserved in the ciphertext. c. In this case, each bit in the ciphertext stream is either the same as the corresponding bit in the key stream or the complement of it. Therefore, the result is also a random string if the key stream is random. d. In this case, the ciphertext is definitely random because the exclusive-or of two random bits results in a random bit. (Continued)
- 55. Figure 5.23 Feedback shift register (FSR) 5.2.1 Continued
- 56. Figure 5.24 LSFR for Example 5.18 5.2.1 Confidentiality
- 57. Example 5.19 5.2.1 Continued Create a linear feedback shift register with 4 cells in which b4 = b1 b0. Show the value of output for 20 transitions (shifts) if the seed is (0001)2. Solution Figure 5.25 LFSR for Example 5.19
- 58. Table 4.6 Cell values and key sequence for Example 5.19 5.2.1 Continued Example 5.19 (Continued)
- 59. Table 4.6 Continued 5.2.1 Continued Example 5.19 (Continued)
- 60. 5.2.1 Continued Note that the key stream is 100010011010111 10001…. This looks like a random sequence at first glance, but if we go through more transitions, we see that the sequence is periodic. It is a repetition of 15 bits as shown below: The key stream generated from a LFSR is a pseudorandom sequence in which the the sequence is repeated after N bits. The maximum period of an LFSR is to 2m − 1. Note Example 5.19 (Continued)
- 61. In a nonsynchronous stream cipher, each key in the key stream depends on previous plaintext or ciphertext. 5.2.2 Nonsynchronous Stream Ciphers In a nonsynchronous stream cipher, the key depends on either the plaintext or ciphertext. Note