Kinemetics
- 1. For more information visit http://jeemains2018.in Inertial frame of reference- Reference frame in which Newtonian mechanics holds are called inertial reference frames or inertial frames. Reference frame in which Newtonian mechanics does not hold are called non-inertial reference frames or non-inertial frames. The average speed vav and average velocity of a body during a time interval ?t is defined as, vav= average speed = ?s/?t Instantaneous speed and velocity are defined at a particular instant and are given by Note: a) A change in either speed or direction of motion results in a change in velocity (b) A particle which completes one revolution, along a circular path, with uniform speed is said to possess zero velocity and non-zero speed. (c) It is not possible for a particle to possess zero speed with a non-zero velocity. Average acceleration is defined as the change in velocity over a time interval?t. The instantaneous acceleration of a particle is the rate at which its velocity is changing at that instant.
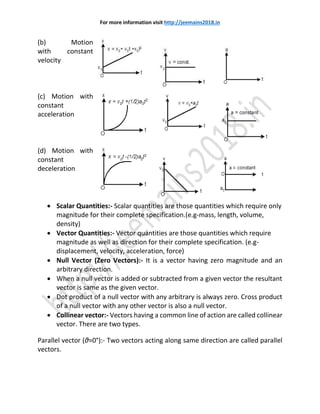
- 2. For more information visit http://jeemains2018.in The three equations of motion for an object with constant acceleration are given below. (a) v= u+at (b) s= ut+1/2 at2 (c) v2 =u2 +2as Here u is the initial velocity, v is the final velocity, a is the acceleration, s is the displacement travelled by the body and t is the time. Note: Take ‘+ve’ sign for a when the body accelerates and takes ‘–ve’ sign when the body decelerates. The displacement by the body in nth second is given by, sn= u + a/2 (2n-1) Position-time (x vs t), velocity-time (v vs t) and acceleration-time (a vs t) graph for motion in one-dimension: (i) Variation of displacement (x), velocity (v) and acceleration (a) with respect to time for different types of motion. Displacement(x) Velocity(v) Acceleration (a) (a) At rest
- 3. For more information visit http://jeemains2018.in (b) Motion with constant velocity (c) Motion with constant acceleration (d) Motion with constant deceleration Scalar Quantities:- Scalar quantities are those quantities which require only magnitude for their complete specification.(e.g-mass, length, volume, density) Vector Quantities:- Vector quantities are those quantities which require magnitude as well as direction for their complete specification. (e.g- displacement, velocity, acceleration, force) Null Vector (Zero Vectors):- It is a vector having zero magnitude and an arbitrary direction. When a null vector is added or subtracted from a given vector the resultant vector is same as the given vector. Dot product of a null vector with any arbitrary is always zero. Cross product of a null vector with any other vector is also a null vector. Collinear vector:- Vectors having a common line of action are called collinear vector. There are two types. Parallel vector (θ=0°):- Two vectors acting along same direction are called parallel vectors.
- 4. For more information visit http://jeemains2018.in Anti-parallel vector (θ=180°):-Two vectors which are directed in opposite directions are called anti-parallel vectors. Co-planar vectors- Vectors situated in one plane, irrespective of their directions, are known as co-planar vectors. Vector addition:- Vector addition is commutative- Vector addition is associative- Vector addition is distributive- Triangles Law of Vector addition:- If two vectors are represented by two sides of a triangle, taken in the same order, then their resultant in represented by the third side of the triangle taken in opposite order. Magnitude of resultant vector :- R=√(A2 +B2 +2ABcosθ) Here θ is the angle between and . If β is the angle between and , then,
- 5. For more information visit http://jeemains2018.in If three vectors acting simultaneously on a particle can be represented by the three sides of a triangle taken in the same order, then the particle will remain in equilibrium. So, Parallelogram law of vector addition:- R=√(A2 +B2 +2ABcosθ), Cases 1:- When, θ=0°, then, R= A+B (maximum), β=0° Cases 2:- When, θ=180°, then, R= A-B (minimum), β=0° Cases 3:- When, θ=90°, then, R=√(A2 +B2 ), β = tan-1 (B/A) The process of subtracting one vector from another is equivalent to adding, vector ally, the negative of the vector to be subtracted. So, Resolution of vector in a plane:-
- 6. For more information visit http://jeemains2018.in Product of two vectors:- (a) Dot product or scalar product:- , Here A is the magnitude of , B is the magnitude of and θ is the angle between and . (i) Perpendicular vector:- (ii) Collinear vector:- When, Parallel vector (θ=0°), When, Anti parallel vector (θ=180°), (b) Cross product or Vector product:- Or,
- 7. For more information visit http://jeemains2018.in Here A is the magnitude of , B is the magnitude of ,θ is the angle between and and is the unit vector in a direction perpendicular to the plane containing and . (i) Perpendicular vector (θ=90°):- (ii) Collinear vector:- When, Parallel vector (θ=0°), (null vector) When, θ=180°, (null vector) Unit Vector- Unit vector of any vector is a vector having a unit magnitude, drawn in the direction of the given vector. In three dimension, Area:- Area of triangle:- Area of parallelogram:- Volume of parallelepiped:- Equation of Motion in an Inclined Plane:
- 8. For more information visit http://jeemains2018.in (i) Perpendicular vector :- At the top of the inclined plane (t = 0, u = 0 and a = g sinq ), the equation of motion will be, (a) v= (g sinθ)t (b) s = ½ (g sinθ) t2 (c) v2 = 2(g sinθ)s (ii) If time taken by the body to reach the bottom is t, then s = ½ (g sinθ) t2 t = √(2s/g sinθ) But sinθ =h/s or s= h/sinθ So, t =(1/sinθ) √(2h/g) (iii) The velocity of the body at the bottom v=g(sinθ)t =√2gh The relative velocity of object A with respect to object B is given by VAB=VA-VB Here, VB is called reference object velocity.
- 9. For more information visit http://jeemains2018.in Variation of mass:- In accordance to Einstein’s mass-variation formula, the relativistic mass of body is defined as, m= m0/√(1-v2 /c2 ) Here, m0 is the rest mass of the body, v is the speed of the body and c is the speed of light. Projectile motion in a plane:- If a particle having initial speed u is projected at an angle θ (angle of projection) with x-axis, then, Time of Flight, T = (2u sinα)/g Horizontal Range, R = u2 sin2α/g Maximum Height, H = u2 sin2 α/2g Equation of trajectory, y = xtanα-(gx2 /2u2 cos2 α) Motion of a ball:- (a) When dropped:- Time period, t=√(2h/g) and speed, v=√(2gh (b) When thrown up:- Time period, t=u/g and height, h = u2 /2g Condition of equilibrium:- (a) (b) |F1+F2|≥|F3|≥| F1-F2|
- 10. For more information visit http://jeemains2018.in