Learning Probabilistic Relational Models using Non-Negative Matrix Factorization
- 1. Anthony Coutant, Philippe Leray, Hoel Le Capitaine DUKe (Data, User, Knowledge) Team, LINA 26th June, 2014 Learning Probabilistic Relational Models using Non-Negative Matrix Factorization 7ème Journées Francophones sur les Réseaux Bayésiens et les Modèles Graphiques Probabilistes
- 2. 22 / 24 Context • Probabilistic Relational Models (PRM) – Attributes uncertainty in Relational datasets • Relational datasets: attributes + link • PRM with Reference Uncertainty (RU) model link uncertainty • Partitioning individuals necessary in PRM-RU
- 3. 33 / 24 Problem & Proposal • PRM-RU partition individuals based on attributes only • We propose to cluster the relationship information instead • We show that : – Attributes partitioning do not explain all relationships – Relational partitioning can explain attributes oriented relationships
- 4. 44 / 24 Flat datasets – Bayesian Networks • Individuals supposed i.i.d. P(G1) A B 0,25 0,75 P(G2) A B 0,25 0,75 Dataset G1 G2 R A B 1st B A 1st B B 2nd B B 2nd G1, G2 P(R|G1,G2) A,A A,B B,A B,B 1st division 0,8 0,5 0,5 0,2 2nd division 0,2 0,5 0,5 0,8 Grade 1 Ranking Grade 2
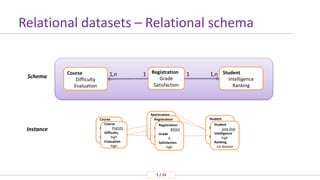
- 5. 55 / 24 Relational datasets – Relational schema Student Intelligence Ranking Registration Grade Satisfaction 1,n1 Instance Schema Course Phil101 Difficulté ??? Note ??? Registration #4563 Note ??? Satisfaction ??? Student Jane Doe Intelligence ??? Classement ??? Student Jane Doe Intelligence high Ranking 1st division Registration #4563 Note ??? Satisfaction ??? Registration #4563 Grade A Satisfaction high Course Phil101 Difficulty high Evaluation high Course Difficulty Evaluation 1,n 1
- 6. 66 / 24 Probabilistic Relational Models (PRM) . MEAN(G) P(R|MEAN(G)) A B 1st division 0,8 0,2 2nd division 0,2 0,8 PRM Schema Instance Student Intelligence Ranking Registration Grade Satisfaction 1,n1Course Difficulty Evaluation 1,n 1 Evaluation Intelligence Grade Satisfaction Difficulty Ranking Course Registration Student MEAN MEAN Course Math Difficulté ??? Note ??? Registration #6251 Note ??? Satisfaction ??? Student John Smith Intelligence ??? Classement ??? Student Jane Doe Intelligence ??? Ranking ??? Registration #5621 Note ??? Satisfaction ??? Registration #4563 Grade ??? Satisfaction ??? Course Phil Difficulty ??? Evaluation ??? Instance
- 7. 77 / 24 Probabilistic Relational Models (PRM) .. MEAN(G) P(R|MEAN(G)) A B 1st division 0,8 0,2 2nd division 0,2 0,8 PRM Schema Course Math Difficulté ??? Note ??? Registration #6251 Note ??? Satisfaction ??? Student John Smith Intelligence ??? Classement ??? Student Jane Doe Intelligence ??? Ranking ??? Registration #5621 Note ??? Satisfaction ??? Registration #4563 Grade ??? Satisfaction ??? Course Phil Difficulty ??? Evaluation ??? Instance Evaluation Intelligence Grade Satisfaction Difficulty Ranking Course Registration Student MEAN MEAN Math.Diff #4563.Grade #5621.Grade #6251.Grade MEAN GBN (Ground Bayesian Network) Math.Eval Phil.Diff Phil.Eval #4563.Satis #5621.Satis #6251.Satis MEAN JD.Int JS.Int JD.Rank JS.Rank MEAN MEAN Instance Student Intelligence Ranking Registration Grade Satisfaction 1,n1Course Difficulty Evaluation 1,n 1
- 8. 88 / 24 Uncertainty in Relational datasets Course Phil101 Difficulté ??? Note ??? Registration #4563 Note ??? Satisfaction ??? Student Jane Doe Intelligence ??? Classement ??? Student Jane Doe Intelligence ??? Ranking ??? Registration #4563 Note ??? Satisfaction ??? Registration #4563 Grade ??? Satisfaction ??? Course Phil101 Difficulty ??? Evaluation ??? Student Jane Doe Intelligence ??? Ranking ??? Student Jane Doe Intelligence ??? Ranking ??? Registration #4563 Note ??? Satisfaction ??? Registration #4563 Grade A Satisfaction ??? Course Phil101 Difficulté ??? Note ??? Course Phil101 Difficulty ??? Evaluation high Course Phil101 Difficulté ??? Note ??? Registration #4563 Note ??? Satisfaction ??? Student Jane Doe Intelligence ??? Classement ??? Student Jane Doe Intelligence ??? Ranking ??? Registration #4563 Note ??? Satisfaction ??? Registration #4563 Grade ??? Satisfaction ??? Course Phil101 Difficulty ??? Evaluation ??? Student Jane Doe Intelligence ??? Ranking ??? Student Jane Doe Intelligence ??? Ranking ??? Registration #4563 Note ??? Satisfaction ??? Registration #4563 Grade A Satisfaction ??? Course Phil101 Difficulté ??? Note ??? Course Phil101 Difficulty ??? Evaluation high ? Attributes uncertainty (PRM) Attributes and link uncertainty (PRM extensions) ?
- 9. 99 / 24 • Reference uncertainty: P(r.Course = ci, r.Student = sj | r.exists = true) • A random variable for each individual id? Not generalizable • Solution: partitioning Difficulty Intelligence Course Student Registration Student Evaluation RankingCourse P(Student | Course.Difficulty)? P(Course)? PRM with reference uncertainty .
- 10. 1010 / 24 • P(Student | ClusterStudent) follows a uniform law Difficulty Intelligence Course Student Registration ClusterCourse Course ClusterStudent Student P(CStudent | S.Intelligence) low high C1 0 1 C2 1 0 P(Student | CStudent) C1 C2 s1 0 1 s2 1 0 Evaluation Ranking PRM with reference uncertainty ..
- 11. 1111 / 24 • P(Student | ClusterStudent) follows a uniform law Difficulty Intelligence Course Student Registration ClusterCourse Course ClusterStudent Student P(CStudent | S.Intelligence) low high C1 0 1 C2 1 0 P(Student | CStudent) C1 C2 s1 0 1 s2 1 0 Evaluation Ranking PRM with reference uncertainty .. highlow Biolow high C1 C2 Students Population stats 50% 50% Partition Function
- 12. 1212 / 24 Attributes-oriented Partition Functions in PRM-RU • PRM-RU: Clustering from attributes • Assumption: attributes explain the relationship • Not generalizable, relationship information not used for partitioning Course Student P(Green | Red) = 1 P(Purple | Blue) = 1 YES
- 13. 1313 / 24 Attributes-oriented Partition Functions in PRM-RU • PRM-RU: Clustering from attributes • Assumption: attributes explain the relationship • Not generalizable, relationship information not used for partitioning Course Student P(Green | Red) = 1 P(Purple | Blue) = 1 Course Student P(Green | Red) = 1 P(Purple | Blue) = 1 YES IS THAT SO?
- 14. 1414 / 24 Attributes-oriented Partition Functions in PRM-RU • PRM-RU: Clustering from attributes • Assumption: attributes explain the relationship • Not generalizable, relationship information not used for partitioning Course Student Course Student P(Green | Red) = 1 P(Purple | Blue) = 1 P(Green | Red) = 0.5 P(Purple | Red) = 0.5 Course Student P(Green | Red) = 0.5 P(Purple | Red) = 0.5 Course Student P(Green | Red) = 1 P(Purple | Blue) = 1 YES NOIS THAT SO?
- 15. 1515 / 24 Relationship-oriented Partitioning • Objective: finding partitioning maximizing intra-partition edges Course Student P(Student.p1 | Course.p1) = 1 P(Student.p2 | Course.p2) = 1 p1 p2 Course Student P(Green | Red) = 0.5 P(Purple | Red) = 0.5
- 16. 1616 / 24 Experiments – Protocol – Dataset generation Entity 2 Att 1 … Att n R 1,n 1 Entity 1 Att 1 … Att n 1 1,n Schema Instance Entity 1 Entity 2R
- 17. 1717 / 24 Experiments – Protocol – Dataset generation Entity 2 Att 1 … Att n R 1,n 1 Entity 1 Att 1 … Att n 1 1,n Schema Instance Entity 1 Entity 2 Attributes partitioning favorable case Relationship partitioning favorable case Entity 1 Entity 2 R R
- 18. 1818 / 24 Experiments – Protocol – Learning Entity 1 Entity 2Relation Att n Att 1 Att n Att 1 CE1 CE2 E2 E1 • Parameter learning on set up structure • 2 PRM compared: – Either with attributes partitioning – Or with relational partitioning
- 19. 1919 / 24 Experiments – Protocol – Evaluation • For each generated dataset D – Split D into 10 subsets {D1, …, D10} – Perform 10 Folds CV each with one Di for test and others for training • Do it for PRM with attributes partitioning : store the results of 10 log likelihood PattsLL[i] • Do it for PRM with relationship partitioning : store the results of 10 log likelihood PrelLL[i] – Evaluate mean and sd of PattsLL[i] and PrelLL[i] – Evaluate significancy of relationship partitioning over attributes partitioning
- 20. 2020 / 24 Experiments – Results Random clusters (independent from attributes) k 2 4 16 n 25 50 100 200 Relational > Attributes partitioning Attributes > Relational partitioning Partitionings not significantly comparable k 2 4 16 n 25 50 100 200 Attributes => Cluster (fully dependent from attributes) Green: Red: Orange:
- 21. 2121 / 24 Experiments – About the NMF choice for partitioning • NMF – Find low dimension factor matrices which product approximates the original matrix – A relationship between two entities is an adjacency matrix • Motivation for NMF usage – (Restrictively) captures latent information from both rows and columns: co-clustering – Several extensions dedicated to more accurate co-clustering (NMTF) – Extensions for Laplacian regularization • Allow to capture both attributes and relationship information for clustering – Extensions for Tensor factorization • Allow to model n-ary relationships, n >= 2 – NMF = Good starting choice for the long-term needs?
- 22. 2222 / 24 Experiments – About the NMF choice for partitioning • But – Troubles with performances in experimentations – Very sensitive to initialization: crashes whenever reaching singular state – Moving toward large scale methods : graph based relational clustering?
- 23. 2323 / 24 Conclusion • PRM-RU to define probability structure in relational datasets • Need for partitioning • PRM-RU use attributes oriented partitioning • We propose to cluster the relationship information instead • Experiments show that : – Attributes partitioning do not explain all relationships – Relational partitioning can explain attributes oriented relationships
- 24. 2424 / 24 Perspectives • Experiments on real life datasets • Towards large scale partitioning methods • PRM-RU Structure Learning using clustering algorithms • What about other link uncertainty representations?
- 25. Anthony Coutant, Philippe Leray, Hoel Le Capitaine DUKe (Data, User, Knowledge) Team, LINA Questions? 7ème Journées Francophones sur les Réseaux Bayésiens et les Modèles Graphiques Probabilistes (anthony.coutant | philippe.leray | hoel.lecapitaine) @univ-nantes.fr
Editor's Notes
- #3: Beaucoup de jeux de données relationnels impliquant individus de différents types + diverses relations entre eux. Besoin d’algorithmes spécifiques pour l’apprentissage, car relaxent hypothèse i.i.d faite généralement PRM sont une extension des RB pour les données relationnelles Les PRM classiques gèrent l’incertitude au niveau des attributs de chaque individu, supposant les relations connues Hors, un jeu de données relationnel comporte à la fois une notion descriptive des entités (attributs) et une dimension topologique (la façon dont les individus sont connectés) Il est important de gérer l’incertitude topologique en plus de l’incertitude d’attributs Plusieurs extensions des PRM pour cela : PRM-RU, PRM-EU … PRM-RU est intéressante car elle expose de façon claire le besoin d’un partitionnement pour s’abstraire d’un jeu de données On s’intéresse ici à la question du choix d’un partitionnement, et de son impact sur l’apprentissage de ces PRM-RU.
- #4: La définition et l’apprentissage d’un PRM-RU nécessite de partitionner les individus impliqués dans une relation. Toutefois, la seule technique de partitionnement définie dans la littérature repose uniquement sur les attributs des individus. Conséquence : la topologie réelle de la relation n’est pas prise en compte pour modéliser l’incertitude de liens entre individus ! Nous proposons de partitionner les individus de façon topologique en lieu et place de l’approche historique. Nous montrons de façon expérimentale que : 1) un partitionnement orienté attributs n’explique pas toutes les relations; 2) un partitionnement relationnel peut expliquer à la fois des relations indépendantes des attributs, mais aussi des relations expliquées par les attributs.
- #5: Beaucoup d’algorithmes d’apprentissage automatique supposent que les données considérées sont i.i.d. (identiquement et indépendamment distribuées). De tels jeux de données peuvent être représentés par des tableaux individus x attribut. Ici, par exemple, je considère un jeu de données où chaque ligne représente les résultats scolaires d’un étudiant. Un réseau Bayésien sur ce jeu de données peut exprimer des dépendances / indépendances probabilistes entre les attributs d’un unique étudiant. Je peux par exemple exprimer le fait que le classement d’un étudiant dépende de ses notes. En revanche, je ne peux pas exprimer la dépendance entre le classement d’un étudiant, et le classement de ses pairs.
- #6: Les jeux de données relationnels sont plus complexes. Un jeu de données ne respecte plus seulement la définition d’un ensemble d’attributs de façon tabulaire, mais obéit aux lois d’un schéma relationnel. Le schéma relationnel décrit l’ensemble des types d’entités existant dans les données, les attributs décrivant ces entités, et les types de relations possibles entre eux. Si nous étendons le jeu de données précédent, nous pouvons par exemple définir une relation entre des individus étudiants et des individus cours, de type « inscription », chaque entité et relation étant décrite par divers attributs. Une instance de ce schéma est alors un jeu de données qui respecte ce schéma. Un exemple en est donné en bas.
- #7: Un PRM est un modèle graphique probabiliste dirigé défini sur un schéma relationnel. Il représente un patron de distribution de probabilités défini sur l’ensemble des instances possibles de ce schéma.
- #8: Etant donné un PRM et une instance respectant le même schéma relationnel, il est possible de créer un Réseau Bayésien déroulé, mis à plat, appelé « Ground Bayesian Network » qui permet de faire de l’inférence sur les valeurs d’attributs des différents individus du jeu de données considéré.
- #9: Les PRM ne gèrent que l’incertitude au niveau des attributs des différents individus, et supposent les relations entre ces individus connus. Notre but est par exemple, en haut, de trouver quelle est la difficulté probable d’un cours en fonction des différents étudiants qui y sont inscrits, et les notes qu’ils ont obtenus sur ce cours. Mais il peut être intéressant de gérer le cas où les relations sont également incertaines, pour faire de la détection automatique de liens. Par exemple, en bas, nous pourrions vouloir trouver l’étudiant le plus probablement attaché à un lien d’inscription concernant un cours particulier, étant donné les caractéristiques du cours, de l’inscription, et des étudiants candidats. Des extensions des PRM existent pour cela.
- #10: Parmi les extensions des PRM, les PRM avec incertitude de référence essaient de modéliser l’incertitude de liens par une distribution de probabilités de type P(endpoints | existence du lien). Cette extension ajoute pour cela des distributions sur l’ensemble des individus possibles au niveau de chaque relation. La question à laquelle il faut maintenant répondre concerne le choix de la structure probabiliste. Naïvement, on pourrait tenter d’apprendre une distribution de probabilités sur l’ensemble des clés des individus impliqués. Toutefois, cela n’est pas généralisable. Une solution proposée dans les PRM-RU pour pallier ce problème, est de partitionner les individus impliqués dans la relation.
- #11: Nous introduisons donc 2 variables aléatoires au total pour chaque point d’entrée d’une relation. L’idée est alors de choisir un individu dans un processus en 2 temps : 1) choisir un groupe d’individus selon une distribution de probabilités définie; 2) choisir aléatoirement un individu de ce groupe, selon une loi uniforme. La complexité du choix est alors réduite car les dimensions des distributions à apprendre au niveau des variables de partitionnement sont très réduites.
- #12: Il ne reste plus qu’à effectivement partitionner les individus. Pour chaque variable « cluster », il faut associer une fonction de partition permettant de regrouper les individus. La variable « cluster » est alors défini sur l’ensemble des clusters de cette fonction.
- #13: Le problème dans les PRM-RU provient de la façon dont sont définies les fonctions de partition, où les seuls attributs des individus de l’entité considérés sont utilisés. L’hypothèse faite est alors très forte : on considère que la relation est pleinement expliquée par les attributs des types d’entités liés. Paradoxalement, cela signifie que l’apprentissage des variables permettant de faire de la détection de liens n’utilisent pas directement les liens du jeu de données d’apprentissage. Cela n’est pas généralisable dans tous les cas. Prenons par exemple le graphe biparti ci-dessous, instance de la relation binaire définie précédemment entre les étudiants et les cours. Je considère ici que deux individus d’une même couleur ont la même configuration d’attributs. Ici, si je tente d’apprendre des distributions sur ma relation, les attributs seuls vont me permettre un bon apprentissage, car tous les cours rouges sont liés à tous les étudiants verts et tous les cours bleus sont liés à tous les étudiants violets. Les distributions de probabilité sont alors informatives et discriminantes.
- #14: Si je prends un second exemple, ce n’est plus si clair. Je vais ainsi toujours apprendre les mêmes distributions de probabilité que précédemment, disant que si un lien est lié à un cours rouge, alors il va nécessairement être lié à un étudiant vert. Toutefois, cela signifie qu’une fois le choix de la couleur et donc du groupe effectué, je peux prendre aléatoirement n’importe quel individu vert. Or, la topologie de la relation exhibe 4 composantes connexes différentes, séparant les deux individus rouges et verts, m’informant que chaque individu d’une paire colorée doit être traitée différemment pour cette relation.
- #15: Dans le dernier cas, la relation est encore plus mélangée et les distributions apprises ne sont plus informatives. J’ai des composantes connexes intéressantes, mais elle sont masquées par des distributions de probabilités consensuelles entre les individus colorées.
- #16: Notre but est de partitionner les individus d’une relation de telle façon que le nombre de liens à l’intérieur de chaque groupe soit maximal. À partir de ce partitionnement, notre but est d’apprendre des distributions de probabilités qui reflètent le plus fidèlement possible la topologie de la relation. Si je reprends le dernier exemple de la slide précédente, je pourrais obtenir un meilleur apprentissage de paramètres en découpant mes individus selon les composantes du graphe, et non pas selon les couleurs des individus.
- #17: Nous avons souhaité confronté les deux techniques de partitionnement et leur impact sur l’apprentissage d’un PRM-RU. Pour cela, nous avons construit deux types de jeux de données. Chacun de ces jeux de données respecte le même schéma relationnel simple, composé d’une seule relation binaire entre deux entités. Chacun de ces jeux de données exhibe différents sous-groupes, avec des préférences fortes pour d’autres sous-groupes de l’autre entité.
- #18: La différence entre les deux jeux de données provient de la répartition des individus dans ces sous-groupes. Le premier jeu de données défini une implication totale entre la valeur des attributs d’un individu et son appartenance à un groupe. Le second jeu de données défini une indépendance totale entre attributs et groupe affecté. Le premier jeu est censé favoriser l’approche de partitionnement par attributs, et l’autre est censé favoriser l’approche orientée relation.
- #19: La comparaison a été faite entre deux apprentissage de paramètres d’une structure fixée de PRM. Deux versions de PRM ont été considérées : une avec un partitionnement par attributs, l’autre avec un partitionnement relationnel.
- #20: Le protocole d’évaluation est le suivant : 1) découper un jeu de données en 10 parties. 2) Faire un apprentissage en validation croisée en 10 étapes en prenant chaque fois un jeu de données comme jeu de tests. 3) Stocker les 10 log vraisemblances calculées pour le PRM avec partitionnement attributs. Faire de même pour le PRM avec partitionnement relationnel. 4) Evaluer la significativité des résultats par un z-test.
- #21: Les résultats obtenus pour chaque jeu de données sont les suivants. Un carré vert indique que l’approche relationnelle est significativement meilleure que l’approche par attributs. Un carré rouge exprime l’idée inverse. Un carré orange montre une zone où le test statistique ne permet pas de trancher. Dans le cas d’un jeu de données avec groupes indépendants des attributs, à gauche ici, on peut voir que notre méthode est significativement meilleure sauf lorsque le ratio n / k est très faible. Des phénomènes de sur apprentissage peuvent expliquer ce comportement. De l’autre côté, lorsque les attributs expliquent une relation, nous ne pouvons pas discerner de schéma clair. Nous pouvons donc dire que notre méthode s’applique autant que la méthode historique pour ces relations. Notre approche semble donc plus généralisable.
- #22: Avant de conclure, je voulais parler de la méthode de partitionnement que nous avons choisi à l’écriture de ce papier pour l’approche relationnelle. Nous avons choisi une implémentation de NMF minimisant une KL-divergence car c’est une technique de factorisation qui a été montrée équivalente à pLSA, nous donnant une interprétation solide en terme de probabilités pour notre problème. Nous avons fait ce choix à l’origine pour diverses raisons autres que la seule interprétabilité. (cf. slide pour la suite)

















![1919 / 24
Experiments – Protocol – Evaluation
• For each generated dataset D
– Split D into 10 subsets {D1, …, D10}
– Perform 10 Folds CV each with one Di for test and others for training
• Do it for PRM with attributes partitioning : store the results of 10 log likelihood PattsLL[i]
• Do it for PRM with relationship partitioning : store the results of 10 log likelihood PrelLL[i]
– Evaluate mean and sd of PattsLL[i] and PrelLL[i]
– Evaluate significancy of relationship partitioning over attributes partitioning](https://image.slidesharecdn.com/presentationv1-140715104158-phpapp02/85/Learning-Probabilistic-Relational-Models-using-Non-Negative-Matrix-Factorization-19-320.jpg)





