Lesson 1: Functions and their representations (slides)
3 likes1,604 views
The document outlines the fundamentals of functions in calculus, including their definitions, representations, and properties. It discusses various ways to express functions, such as through formulas, numeric tables, graphs, and verbal descriptions, while also introducing the concepts of monotonicity and symmetry. The importance of functions in modeling real-world problems and their different types, such as piecewise-defined functions, is emphasized.
![Piecewise-defined functions
Example Solu on
Let The domain is [0, 2]. The graph
{ can be drawn piecewise.
x2 0 ≤ x ≤ 1;
f(x) = 2
3−x 1 < x ≤ 2.
1
Find the domain and range of f
and graph the func on. .
0 1 2](https://image.slidesharecdn.com/lesson01-functions001slides-110124144728-phpapp02/85/Lesson-1-Functions-and-their-representations-slides-23-320.jpg)
![Piecewise-defined functions
Example Solu on
Let The domain is [0, 2]. The graph
{ can be drawn piecewise.
x2 0 ≤ x ≤ 1;
f(x) = 2
3−x 1 < x ≤ 2.
1
Find the domain and range of f
and graph the func on. .
0 1 2](https://image.slidesharecdn.com/lesson01-functions001slides-110124144728-phpapp02/85/Lesson-1-Functions-and-their-representations-slides-24-320.jpg)
![Piecewise-defined functions
Example Solu on
Let The domain is [0, 2]. The graph
{ can be drawn piecewise.
x2 0 ≤ x ≤ 1;
f(x) = 2
3−x 1 < x ≤ 2.
1
Find the domain and range of f
and graph the func on. .
0 1 2](https://image.slidesharecdn.com/lesson01-functions001slides-110124144728-phpapp02/85/Lesson-1-Functions-and-their-representations-slides-25-320.jpg)
![Piecewise-defined functions
Example Solu on
Let The domain is [0, 2]. The graph
{ can be drawn piecewise.
x2 0 ≤ x ≤ 1;
f(x) = 2
3−x 1 < x ≤ 2.
1
Find the domain and range of f
and graph the func on. .
0 1 2
The range is [0, 2).](https://image.slidesharecdn.com/lesson01-functions001slides-110124144728-phpapp02/85/Lesson-1-Functions-and-their-representations-slides-26-320.jpg)
Lesson 1: Functions and their representations (slides)
- 1. . Sec on 1.1 Func ons and their Representa ons V63.0121.001, Calculus I Professor Ma hew Leingang New York University Announcements First WebAssign-ments are due January 31 Do the Get-to-Know-You survey for extra credit!
- 2. Section 1.1 Functions and their Representations V63.0121.001, Calculus I Professor Ma hew Leingang New York University
- 3. Announcements First WebAssign-ments are due January 31 Do the Get-to-Know-You survey for extra credit!
- 4. Objectives Understand the defini on of func on. Work with func ons represented in different ways Work with func ons defined piecewise over several intervals. Understand and apply the defini on of increasing and decreasing func on.
- 5. What is a function? Defini on A func on f is a rela on which assigns to to every element x in a set D a single element f(x) in a set E. The set D is called the domain of f. The set E is called the target of f. The set { y | y = f(x) for some x } is called the range of f.
- 6. Outline Modeling Examples of func ons Func ons expressed by formulas Func ons described numerically Func ons described graphically Func ons described verbally Proper es of func ons Monotonicity Symmetry
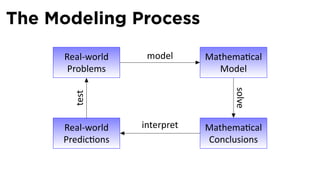
- 7. The Modeling Process Real-world . . model Mathema cal . Problems Model solve test Real-world interpret Mathema cal . . Predic ons Conclusions
- 8. Plato’s Cave .
- 9. The Modeling Process Real-world . . model Mathema cal . Problems Model Shadows Forms solve test Real-world interpret Mathema cal . . Predic ons Conclusions
- 10. Outline Modeling Examples of func ons Func ons expressed by formulas Func ons described numerically Func ons described graphically Func ons described verbally Proper es of func ons Monotonicity Symmetry
- 11. Functions expressed by formulas Any expression in a single variable x defines a func on. In this case, the domain is understood to be the largest set of x which a er subs tu on, give a real number.
- 12. Formula function example Example x+1 Let f(x) = . Find the domain and range of f. x−2
- 13. Formula function example Example x+1 Let f(x) = . Find the domain and range of f. x−2 Solu on The denominator is zero when x = 2, so the domain is all real numbers except 2. We write: domain(f) = { x | x ̸= 2 }
- 14. Formula function example Example x+1 Let f(x) = . Find the domain and range of f. x−2 Solu on x+1 2y + 1 As for the range, we can solve y = =⇒ x = . So as x−2 y−1 long as y ̸= 1, there is an x associated to y. range(f) = { y | y ̸= 1 }
- 15. How did you get that? x+1 start y= x−2
- 16. How did you get that? x+1 start y= x−2 cross-mul ply y(x − 2) = x + 1
- 17. How did you get that? x+1 start y= x−2 cross-mul ply y(x − 2) = x + 1 distribute xy − 2y = x + 1
- 18. How did you get that? x+1 start y= x−2 cross-mul ply y(x − 2) = x + 1 distribute xy − 2y = x + 1 collect x terms xy − x = 2y + 1
- 19. How did you get that? x+1 start y= x−2 cross-mul ply y(x − 2) = x + 1 distribute xy − 2y = x + 1 collect x terms xy − x = 2y + 1 factor x(y − 1) = 2y + 1
- 20. How did you get that? x+1 start y= x−2 cross-mul ply y(x − 2) = x + 1 distribute xy − 2y = x + 1 collect x terms xy − x = 2y + 1 factor x(y − 1) = 2y + 1 2y + 1 divide x= y−1
- 21. No-no’s for expressions Cannot have zero in the denominator of an expression Cannot have a nega ve number under an even root (e.g., square root) Cannot have the logarithm of a nega ve number
- 22. Piecewise-defined functions Example Let { x2 0 ≤ x ≤ 1; f(x) = 3−x 1 < x ≤ 2. Find the domain and range of f and graph the func on.
- 23. Piecewise-defined functions Example Solu on Let The domain is [0, 2]. The graph { can be drawn piecewise. x2 0 ≤ x ≤ 1; f(x) = 2 3−x 1 < x ≤ 2. 1 Find the domain and range of f and graph the func on. . 0 1 2
- 24. Piecewise-defined functions Example Solu on Let The domain is [0, 2]. The graph { can be drawn piecewise. x2 0 ≤ x ≤ 1; f(x) = 2 3−x 1 < x ≤ 2. 1 Find the domain and range of f and graph the func on. . 0 1 2
- 25. Piecewise-defined functions Example Solu on Let The domain is [0, 2]. The graph { can be drawn piecewise. x2 0 ≤ x ≤ 1; f(x) = 2 3−x 1 < x ≤ 2. 1 Find the domain and range of f and graph the func on. . 0 1 2
- 26. Piecewise-defined functions Example Solu on Let The domain is [0, 2]. The graph { can be drawn piecewise. x2 0 ≤ x ≤ 1; f(x) = 2 3−x 1 < x ≤ 2. 1 Find the domain and range of f and graph the func on. . 0 1 2 The range is [0, 2).
- 27. Functions described numerically We can just describe a func on by a table of values, or a diagram.
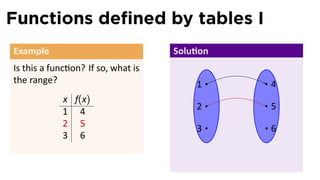
- 28. Functions defined by tables I Example Is this a func on? If so, what is the range? x f(x) 1 4 2 5 3 6
- 29. Functions defined by tables I Example Solu on Is this a func on? If so, what is the range? 1 . 4 x f(x) 2 5 1 4 2 5 3 6 3 6
- 30. Functions defined by tables I Example Solu on Is this a func on? If so, what is the range? 1 . 4 x f(x) 2 5 1 4 2 5 3 6 3 6
- 31. Functions defined by tables I Example Solu on Is this a func on? If so, what is the range? 1 . 4 x f(x) 2 5 1 4 2 5 3 6 3 6
- 32. Functions defined by tables I Example Solu on Is this a func on? If so, what is the range? 1 . 4 x f(x) 2 5 1 4 2 5 3 6 3 6
- 33. Functions defined by tables I Example Solu on Is this a func on? If so, what is the range? 1 . 4 x f(x) 2 5 1 4 2 5 3 6 3 6 Yes, the range is {4, 5, 6}.
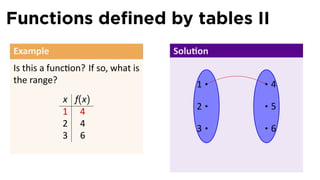
- 34. Functions defined by tables II Example Is this a func on? If so, what is the range? x f(x) 1 4 2 4 3 6
- 35. Functions defined by tables II Example Solu on Is this a func on? If so, what is the range? 1 . 4 x f(x) 2 5 1 4 2 4 3 6 3 6
- 36. Functions defined by tables II Example Solu on Is this a func on? If so, what is the range? 1 . 4 x f(x) 2 5 1 4 2 4 3 6 3 6
- 37. Functions defined by tables II Example Solu on Is this a func on? If so, what is the range? 1 . 4 x f(x) 2 5 1 4 2 4 3 6 3 6
- 38. Functions defined by tables II Example Solu on Is this a func on? If so, what is the range? 1 . 4 x f(x) 2 5 1 4 2 4 3 6 3 6
- 39. Functions defined by tables II Example Solu on Is this a func on? If so, what is the range? 1 . 4 x f(x) 2 5 1 4 2 4 3 6 3 6 Yes, the range is {4, 6}.
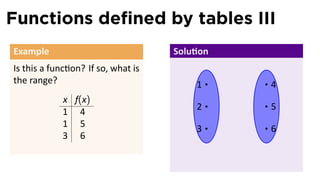
- 40. Functions defined by tables III Example Is this a func on? If so, what is the range? x f(x) 1 4 1 5 3 6
- 41. Functions defined by tables III Example Solu on Is this a func on? If so, what is the range? 1 . 4 x f(x) 2 5 1 4 1 5 3 6 3 6
- 42. Functions defined by tables III Example Solu on Is this a func on? If so, what is the range? 1 . 4 x f(x) 2 5 1 4 1 5 3 6 3 6
- 43. Functions defined by tables III Example Solu on Is this a func on? If so, what is the range? 1 . 4 x f(x) 2 5 1 4 1 5 3 6 3 6
- 44. Functions defined by tables III Example Solu on Is this a func on? If so, what is the range? 1 . 4 x f(x) 2 5 1 4 1 5 3 6 3 6
- 45. Functions defined by tables III Example Solu on Is this a func on? If so, what is the range? 1 . 4 x f(x) 2 5 1 4 1 5 3 6 3 6 This is not a func on.
- 47. An ideal function Domain is the bu ons
- 48. An ideal function Domain is the bu ons Range is the kinds of soda that come out
- 49. An ideal function Domain is the bu ons Range is the kinds of soda that come out You can press more than one bu on to get some brands
- 50. An ideal function Domain is the bu ons Range is the kinds of soda that come out You can press more than one bu on to get some brands But each bu on will only give one brand
- 51. Why numerical functions matter Ques on Why use numerical func ons at all? Formula func ons are so much easier to work with.
- 52. Why numerical functions matter Ques on Why use numerical func ons at all? Formula func ons are so much easier to work with. Answer In science, func ons are o en defined by data. Or, we observe data and assume that it’s close to some nice con nuous func on.
- 53. Numerical Function Example Example Here is the temperature in Boise, Idaho measured in 15-minute intervals over the period August 22–29, 2008. 100 90 80 70 60 50 40 30 20 10 . 8/22 8/23 8/24 8/25 8/26 8/27 8/28 8/29
- 54. Functions described graphically Some mes all we have is the “picture” of a func on, by which we mean, its graph. The graph on the right represents a rela on but not a func on.
- 55. Functions described graphically Some mes all we have is the “picture” of a func on, by which we mean, its graph. . The graph on the right represents a rela on but not a func on.
- 56. Functions described graphically Some mes all we have is the “picture” of a func on, by which we mean, its graph. . . The graph on the right represents a rela on but not a func on.
- 57. Functions described graphically Some mes all we have is the “picture” of a func on, by which we mean, its graph. . . The graph on the right represents a rela on but not a func on.
- 58. Functions described graphically Some mes all we have is the “picture” of a func on, by which we mean, its graph. . . The graph on the right represents a rela on but not a func on.
- 59. Functions described verbally O en mes our func ons come out of nature and have verbal descrip ons: The temperature T(t) in this room at me t.
- 60. Functions described verbally O en mes our func ons come out of nature and have verbal descrip ons: The temperature T(t) in this room at me t. The eleva on h(θ) of the point on the equator at longitude θ.
- 61. Functions described verbally O en mes our func ons come out of nature and have verbal descrip ons: The temperature T(t) in this room at me t. The eleva on h(θ) of the point on the equator at longitude θ. The u lity u(x) I derive by consuming x burritos.
- 62. Outline Modeling Examples of func ons Func ons expressed by formulas Func ons described numerically Func ons described graphically Func ons described verbally Proper es of func ons Monotonicity Symmetry
- 63. Monotonicity Example Let P(x) be the probability that my income was at least $x last year. What might a graph of P(x) look like?
- 64. Monotonicity Example Solu on Let P(x) be the probability that 1 my income was at least $x last year. What 0.5 might a graph of P(x) look like? . $0 $52,115 $100K
- 65. Monotonicity Defini on A func on f is decreasing if f(x1 ) > f(x2 ) whenever x1 < x2 for any two points x1 and x2 in the domain of f. A func on f is increasing if f(x1 ) < f(x2 ) whenever x1 < x2 for any two points x1 and x2 in the domain of f.
- 66. Examples Example Going back to the burrito func on, would you call it increasing?
- 67. Examples Example Going back to the burrito func on, would you call it increasing? Answer Not if they are all consumed at once! Strictly speaking, the insa ability principle in economics means that u li es are always increasing func ons.
- 68. Examples Example Going back to the burrito func on, would you call it increasing? Answer Not if they are all consumed at once! Strictly speaking, the insa ability principle in economics means that u li es are always increasing func ons. Example Obviously, the temperature in Boise is neither increasing nor decreasing.
- 69. Symmetry Consider the following func ons described as words Example Let I(x) be the intensity of light x distance from a point. Example Let F(x) be the gravita onal force at a point x distance from a black hole. What might their graphs look like?
- 70. Possible Intensity Graph Example Solu on Let I(x) be the intensity of light x distance from y = I(x) a point. Sketch a possible graph for I(x). . x
- 71. Possible Gravity Graph Example Solu on Let F(x) be the gravita onal force at a y = F(x) point x distance from a black hole. Sketch a possible graph for F(x). . x
- 72. Definitions Defini on A func on f is called even if f(−x) = f(x) for all x in the domain of f. A func on f is called odd if f(−x) = −f(x) for all x in the domain of f.
- 73. Examples Example Even: constants, even powers, cosine Odd: odd powers, sine, tangent Neither: exp, log
- 74. Summary The fundamental unit of inves ga on in calculus is the func on. Func ons can have many representa ons