Lesson 12: Linear Approximation and Differentials (Section 21 slides)
- 1. Section 2.8 Linear Approximation and Differentials V63.0121.021, Calculus I New York University October 14, 2010 Announcements Quiz 2 in recitation this week on §§1.5, 1.6, 2.1, 2.2 Midterm on §§1.1–2.5 . . . . . .
- 2. Announcements Quiz 2 in recitation this week on §§1.5, 1.6, 2.1, 2.2 Midterm on §§1.1–2.5 . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 2 / 36
- 3. Midterm FAQ Question What sections are covered on the midterm? . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 3 / 36
- 4. Midterm FAQ Question What sections are covered on the midterm? Answer The midterm will cover Sections 1.1–2.5 (The Chain Rule). . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 3 / 36
- 5. Midterm FAQ Question What sections are covered on the midterm? Answer The midterm will cover Sections 1.1–2.5 (The Chain Rule). Question Is Section 2.6 going to be on the midterm? . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 3 / 36
- 6. Midterm FAQ Question What sections are covered on the midterm? Answer The midterm will cover Sections 1.1–2.5 (The Chain Rule). Question Is Section 2.6 going to be on the midterm? Answer The midterm will cover Sections 1.1–2.5 (The Chain Rule). . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 3 / 36
- 7. Midterm FAQ Question What sections are covered on the midterm? Answer The midterm will cover Sections 1.1–2.5 (The Chain Rule). Question Is Section 2.6 going to be on the midterm? Answer The midterm will cover Sections 1.1–2.5 (The Chain Rule). Question Is Section 2.8 going to be on the midterm?... . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 3 / 36
- 8. Midterm FAQ, continued Question What format will the exam take? . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 4 / 36
- 9. Midterm FAQ, continued Question What format will the exam take? Answer There will be both fixed-response (e.g., multiple choice) and free-response questions. . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 4 / 36
- 10. Midterm FAQ, continued Question What format will the exam take? Answer There will be both fixed-response (e.g., multiple choice) and free-response questions. Question Will explanations be necessary? . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 4 / 36
- 11. Midterm FAQ, continued Question What format will the exam take? Answer There will be both fixed-response (e.g., multiple choice) and free-response questions. Question Will explanations be necessary? Answer Yes, on free-response problems we will expect you to explain yourself. This is why it was required on written homework. . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 4 / 36
- 12. Midterm FAQ, continued Question Is (topic X) going to be tested? . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 5 / 36
- 13. Midterm FAQ, continued Question Is (topic X) going to be tested? Answer Everything covered in class or on homework is fair game for the exam. No topic that was not covered in class nor on homework will be on the exam. (This is not the same as saying all exam problems are similar to class examples or homework problems.) . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 5 / 36
- 14. Midterm FAQ, continued Question Will there be a review session? . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 6 / 36
- 15. Midterm FAQ, continued Question Will there be a review session? Answer We’re working on it. . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 6 / 36
- 16. Midterm FAQ, continued Question Will calculators be allowed? . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 7 / 36
- 17. Midterm FAQ, continued Question Will calculators be allowed? Answer No. The exam is designed for pencil and brain. . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 7 / 36
- 18. Midterm FAQ, continued Question How should I study? . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 8 / 36
- 19. Midterm FAQ, continued Question How should I study? Answer The exam has problems; study by doing problems. If you get one right, think about how you got it right. If you got it wrong or didn’t get it at all, reread the textbook and do easier problems to build up your understanding. Break up the material into chunks. (related) Don’t put it all off until the night before. Ask questions. . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 8 / 36
- 20. Midterm FAQ, continued Question How many questions are there? . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 9 / 36
- 21. Midterm FAQ, continued Question How many questions are there? Answer Does this question contribute to your understanding of the material? . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 9 / 36
- 22. Midterm FAQ, continued Question Will there be a curve on the exam? . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 10 / 36
- 23. Midterm FAQ, continued Question Will there be a curve on the exam? Answer Does this question contribute to your understanding of the material? . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 10 / 36
- 24. Midterm FAQ, continued Question When will you grade my get-to-know-you and photo extra credit? . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 11 / 36
- 25. Midterm FAQ, continued Question When will you grade my get-to-know-you and photo extra credit? Answer Does this question contribute to your understanding of the material? . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 11 / 36
- 26. Objectives Use tangent lines to make linear approximations to a function. Given a function and a point in the domain, compute the linearization of the function at that point. Use linearization to approximate values of functions Given a function, compute the differential of that function Use the differential notation to estimate error in linear approximations. . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 12 / 36
- 27. Outline The linear approximation of a function near a point Examples Questions Differentials Using differentials to estimate error Advanced Examples . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 13 / 36
- 28. The Big Idea Question Let f be differentiable at a. What linear function best approximates f near a? . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 14 / 36
- 29. The Big Idea Question Let f be differentiable at a. What linear function best approximates f near a? Answer The tangent line, of course! . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 14 / 36
- 30. The Big Idea Question Let f be differentiable at a. What linear function best approximates f near a? Answer The tangent line, of course! Question What is the equation for the line tangent to y = f(x) at (a, f(a))? . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 14 / 36
- 31. The Big Idea Question Let f be differentiable at a. What linear function best approximates f near a? Answer The tangent line, of course! Question What is the equation for the line tangent to y = f(x) at (a, f(a))? Answer L(x) = f(a) + f′ (a)(x − a) . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 14 / 36
- 32. The tangent line is a linear approximation y . L(x) = f(a) + f′ (a)(x − a) is a decent approximation to f L . (x) . near a. f .(x) . f .(a) . . x−a . x . a . x . . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 15 / 36
- 33. The tangent line is a linear approximation y . L(x) = f(a) + f′ (a)(x − a) is a decent approximation to f L . (x) . near a. f .(x) . How decent? The closer x is to a, the better the approxmation f .(a) . . x−a L(x) is to f(x) . x . a . x . . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 15 / 36
- 34. Example . Example Estimate sin(61◦ ) = sin(61π/180) by using a linear approximation (i) about a = 0 (ii) about a = 60◦ = π/3. . . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 16 / 36
- 35. Example . Example Estimate sin(61◦ ) = sin(61π/180) by using a linear approximation (i) about a = 0 (ii) about a = 60◦ = π/3. Solution (i) If f(x) = sin x, then f(0) = 0 and f′ (0) = 1. So the linear approximation near 0 is L(x) = 0 + 1 · x = x. Thus ( ) 61π 61π sin ≈ ≈ 1.06465 180 180 . . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 16 / 36
- 36. Example . Example Estimate sin(61◦ ) = sin(61π/180) by using a linear approximation (i) about a = 0 (ii) about a = 60◦ = π/3. Solution (i) Solution (ii) (π) We have f = and If f(x) = sin x, then f(0) = 0 ( ) 3 and f′ (0) = 1. f′ π = . 3 So the linear approximation near 0 is L(x) = 0 + 1 · x = x. Thus ( ) 61π 61π sin ≈ ≈ 1.06465 180 180 . . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 16 / 36
- 37. Example . Example Estimate sin(61◦ ) = sin(61π/180) by using a linear approximation (i) about a = 0 (ii) about a = 60◦ = π/3. Solution (i) Solution (ii) (π) √ 3 We have f = and If f(x) = sin x, then f(0) = 0 ( ) 3 2 and f′ (0) = 1. f′ π = . 3 So the linear approximation near 0 is L(x) = 0 + 1 · x = x. Thus ( ) 61π 61π sin ≈ ≈ 1.06465 180 180 . . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 16 / 36
- 38. Example . Example Estimate sin(61◦ ) = sin(61π/180) by using a linear approximation (i) about a = 0 (ii) about a = 60◦ = π/3. Solution (i) Solution (ii) (π) √ 3 We have f = and If f(x) = sin x, then f(0) = 0 ( ) 3 2 and f′ (0) = 1. f′ π = 1 . 3 2 So the linear approximation near 0 is L(x) = 0 + 1 · x = x. Thus ( ) 61π 61π sin ≈ ≈ 1.06465 180 180 . . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 16 / 36
- 39. Example . Example Estimate sin(61◦ ) = sin(61π/180) by using a linear approximation (i) about a = 0 (ii) about a = 60◦ = π/3. Solution (i) Solution (ii) (π) √ 3 We have f = and If f(x) = sin x, then f(0) = 0 ( ) 3 2 and f′ (0) = 1. f′ π = 1 . 3 2 So the linear approximation So L(x) = near 0 is L(x) = 0 + 1 · x = x. Thus ( ) 61π 61π sin ≈ ≈ 1.06465 180 180 . . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 16 / 36
- 40. Example . Example Estimate sin(61◦ ) = sin(61π/180) by using a linear approximation (i) about a = 0 (ii) about a = 60◦ = π/3. Solution (i) Solution (ii) (π) √ 3 We have f = and If f(x) = sin x, then f(0) = 0 ( ) 3 2 and f′ (0) = 1. f′ π = 1 . 3 2 √ So the linear approximation 3 1( π) So L(x) = + x− near 0 is L(x) = 0 + 1 · x = x. 2 2 3 Thus ( ) 61π 61π sin ≈ ≈ 1.06465 180 180 . . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 16 / 36
- 41. Example . Example Estimate sin(61◦ ) = sin(61π/180) by using a linear approximation (i) about a = 0 (ii) about a = 60◦ = π/3. Solution (i) Solution (ii) (π) √ 3 We have f = and If f(x) = sin x, then f(0) = 0 ( ) 3 2 and f′ (0) = 1. f′ π = 1 . 3 2 √ So the linear approximation 3 1( π) So L(x) = + x− near 0 is L(x) = 0 + 1 · x = x. 2 2 3 Thus Thus ( ) ( ) 61π 61π 61π sin ≈ ≈ 1.06465 sin ≈ 180 180 180 . . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 16 / 36
- 42. Example . Example Estimate sin(61◦ ) = sin(61π/180) by using a linear approximation (i) about a = 0 (ii) about a = 60◦ = π/3. Solution (i) Solution (ii) (π) √ 3 We have f = and If f(x) = sin x, then f(0) = 0 ( ) 3 2 and f′ (0) = 1. f′ π = 1 . 3 2 √ So the linear approximation 3 1( π) So L(x) = + x− near 0 is L(x) = 0 + 1 · x = x. 2 2 3 Thus Thus ( ) ( ) 61π 61π 61π sin ≈ ≈ 1.06465 sin ≈ 0.87475 180 180 180 . . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 16 / 36
- 43. Example . Example Estimate sin(61◦ ) = sin(61π/180) by using a linear approximation (i) about a = 0 (ii) about a = 60◦ = π/3. Solution (i) Solution (ii) (π) √ 3 We have f = and If f(x) = sin x, then f(0) = 0 ( ) 3 2 and f′ (0) = 1. f′ π = 1 . 3 2 √ So the linear approximation 3 1( π) So L(x) = + x− near 0 is L(x) = 0 + 1 · x = x. 2 2 3 Thus Thus ( ) ( ) 61π 61π 61π sin ≈ ≈ 1.06465 sin ≈ 0.87475 180 180 180 Calculator check: sin(61◦ ) ≈ . . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 16 / 36
- 44. Example . Example Estimate sin(61◦ ) = sin(61π/180) by using a linear approximation (i) about a = 0 (ii) about a = 60◦ = π/3. Solution (i) Solution (ii) (π) √ 3 We have f = and If f(x) = sin x, then f(0) = 0 ( ) 3 2 and f′ (0) = 1. f′ π = 1 . 3 2 √ So the linear approximation 3 1( π) So L(x) = + x− near 0 is L(x) = 0 + 1 · x = x. 2 2 3 Thus Thus ( ) ( ) 61π 61π 61π sin ≈ ≈ 1.06465 sin ≈ 0.87475 180 180 180 Calculator check: sin(61◦ ) ≈ 0.87462. . . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 16 / 36
- 45. Illustration y . y . = sin x . x . . 1◦ 6 . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 17 / 36
- 46. Illustration y . y . = L1 (x) = x y . = sin x . x . 0 . . 1◦ 6 . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 17 / 36
- 47. Illustration y . y . = L1 (x) = x b . ig difference! y . = sin x . x . 0 . . 1◦ 6 . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 17 / 36
- 48. Illustration y . y . = L1 (x) = x √ ( ) y . = L2 (x) = 2 3 + 1 2 x− π 3 y . = sin x . . . x . 0 . . π/3 . 1◦ 6 . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 17 / 36
- 49. Illustration y . y . = L1 (x) = x √ ( ) y . = L2 (x) = 2 3 + 1 2 x− π 3 y . = sin x . . ery little difference! v . . x . 0 . . π/3 . 1◦ 6 . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 17 / 36
- 50. Another Example Example √ Estimate 10 using the fact that 10 = 9 + 1. . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 18 / 36
- 51. Another Example Example √ Estimate 10 using the fact that 10 = 9 + 1. Solution √ The key step is to use a linear approximation to f(x) = √ x near a = 9 to estimate f(10) = 10. . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 18 / 36
- 52. Another Example Example √ Estimate 10 using the fact that 10 = 9 + 1. Solution √ The key step is to use a linear approximation to f(x) = √ x near a = 9 to estimate f(10) = 10. f(10) ≈ L(10) = f(9) + f′ (9)(10 − 9) 1 19 =3+ (1) = ≈ 3.167 2·3 6 . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 18 / 36
- 53. Another Example Example √ Estimate 10 using the fact that 10 = 9 + 1. Solution √ The key step is to use a linear approximation to f(x) = √ x near a = 9 to estimate f(10) = 10. f(10) ≈ L(10) = f(9) + f′ (9)(10 − 9) 1 19 =3+ (1) = ≈ 3.167 2·3 6 ( )2 19 Check: = 6 . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 18 / 36
- 54. Another Example Example √ Estimate 10 using the fact that 10 = 9 + 1. Solution √ The key step is to use a linear approximation to f(x) = √ x near a = 9 to estimate f(10) = 10. f(10) ≈ L(10) = f(9) + f′ (9)(10 − 9) 1 19 =3+ (1) = ≈ 3.167 2·3 6 ( )2 19 361 Check: = . 6 36 . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 18 / 36
- 55. Dividing without dividing? Example A student has an irrational fear of long division and needs to estimate 577 ÷ 408. He writes 577 1 1 1 = 1 + 169 = 1 + 169 × × . 408 408 4 102 1 Help the student estimate . 102 . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 19 / 36
- 56. Dividing without dividing? Example A student has an irrational fear of long division and needs to estimate 577 ÷ 408. He writes 577 1 1 1 = 1 + 169 = 1 + 169 × × . 408 408 4 102 1 Help the student estimate . 102 Solution 1 Let f(x) = . We know f(100) and we want to estimate f(102). x 1 1 f(102) ≈ f(100) + f′ (100)(2) = − (2) = 0.0098 100 1002 577 =⇒ ≈ 1.41405 408 . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 19 / 36
- 57. Questions Example Suppose we are traveling in a car and at noon our speed is 50 mi/hr. How far will we have traveled by 2:00pm? by 3:00pm? By midnight? . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 20 / 36
- 58. Answers Example Suppose we are traveling in a car and at noon our speed is 50 mi/hr. How far will we have traveled by 2:00pm? by 3:00pm? By midnight? . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 21 / 36
- 59. Answers Example Suppose we are traveling in a car and at noon our speed is 50 mi/hr. How far will we have traveled by 2:00pm? by 3:00pm? By midnight? Answer 100 mi 150 mi 600 mi (?) (Is it reasonable to assume 12 hours at the same speed?) . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 21 / 36
- 60. Questions Example Suppose we are traveling in a car and at noon our speed is 50 mi/hr. How far will we have traveled by 2:00pm? by 3:00pm? By midnight? Example Suppose our factory makes MP3 players and the marginal cost is currently $50/lot. How much will it cost to make 2 more lots? 3 more lots? 12 more lots? . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 22 / 36
- 61. Answers Example Suppose our factory makes MP3 players and the marginal cost is currently $50/lot. How much will it cost to make 2 more lots? 3 more lots? 12 more lots? Answer $100 $150 $600 (?) . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 23 / 36
- 62. Questions Example Suppose we are traveling in a car and at noon our speed is 50 mi/hr. How far will we have traveled by 2:00pm? by 3:00pm? By midnight? Example Suppose our factory makes MP3 players and the marginal cost is currently $50/lot. How much will it cost to make 2 more lots? 3 more lots? 12 more lots? Example Suppose a line goes through the point (x0 , y0 ) and has slope m. If the point is moved horizontally by dx, while staying on the line, what is the corresponding vertical movement? . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 24 / 36
- 63. Answers Example Suppose a line goes through the point (x0 , y0 ) and has slope m. If the point is moved horizontally by dx, while staying on the line, what is the corresponding vertical movement? . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 25 / 36
- 64. Answers Example Suppose a line goes through the point (x0 , y0 ) and has slope m. If the point is moved horizontally by dx, while staying on the line, what is the corresponding vertical movement? Answer The slope of the line is rise m= run We are given a “run” of dx, so the corresponding “rise” is m dx. . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 25 / 36
- 65. Outline The linear approximation of a function near a point Examples Questions Differentials Using differentials to estimate error Advanced Examples . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 26 / 36
- 66. Differentials are another way to express derivatives The fact that the the tangent line is an approximation means that y . f(x + ∆x) − f(x) ≈ f′ (x) ∆x ∆y dy Rename ∆x = dx, so we can write this as . . dy . ∆y ′ ∆y ≈ dy = f (x)dx. . . dx = ∆x Note this looks a lot like the Leibniz-Newton identity . x . dy x x . . + ∆x = f′ (x) dx . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 27 / 36
- 67. Using differentials to estimate error y . Estimating error with differentials If y = f(x), x0 and ∆x is known, and an estimate of ∆y is desired: . . Approximate: ∆y ≈ dy dy . ∆y Differentiate: dy = f′ (x) dx . . dx = ∆x Evaluate at x = x0 and dx = ∆x. . x . x x . . + ∆x . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 28 / 36
- 68. Example A sheet of plywood measures 8 ft × 4 ft. Suppose our plywood-cutting machine will cut a rectangle whose width is exactly half its length, but the length is prone to errors. If the length is off by 1 in, how bad can the area of the sheet be off by? . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 29 / 36
- 69. Example A sheet of plywood measures 8 ft × 4 ft. Suppose our plywood-cutting machine will cut a rectangle whose width is exactly half its length, but the length is prone to errors. If the length is off by 1 in, how bad can the area of the sheet be off by? Solution 1 2 Write A(ℓ) = ℓ . We want to know ∆A when ℓ = 8 ft and ∆ℓ = 1 in. 2 . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 29 / 36
- 70. Example A sheet of plywood measures 8 ft × 4 ft. Suppose our plywood-cutting machine will cut a rectangle whose width is exactly half its length, but the length is prone to errors. If the length is off by 1 in, how bad can the area of the sheet be off by? Solution 1 2 Write A(ℓ) = ℓ . We want to know ∆A when ℓ = 8 ft and ∆ℓ = 1 in. 2 ( ) 97 9409 9409 (I) A(ℓ + ∆ℓ) = A = So ∆A = − 32 ≈ 0.6701. 12 288 288 . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 29 / 36
- 71. Example A sheet of plywood measures 8 ft × 4 ft. Suppose our plywood-cutting machine will cut a rectangle whose width is exactly half its length, but the length is prone to errors. If the length is off by 1 in, how bad can the area of the sheet be off by? Solution 1 2 Write A(ℓ) = ℓ . We want to know ∆A when ℓ = 8 ft and ∆ℓ = 1 in. 2 ( ) 97 9409 9409 (I) A(ℓ + ∆ℓ) = A = So ∆A = − 32 ≈ 0.6701. 12 288 288 dA (II) = ℓ, so dA = ℓ dℓ, which should be a good estimate for ∆ℓ. dℓ When ℓ = 8 and dℓ = 12 , we have dA = 12 = 2 ≈ 0.667. So we 1 8 3 get estimates close to the hundredth of a square foot. . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 29 / 36
- 72. Why? Why use linear approximations dy when the actual difference ∆y is known? Linear approximation is quick and reliable. Finding ∆y exactly depends on the function. These examples are overly simple. See the “Advanced Examples” later. In real life, sometimes only f(a) and f′ (a) are known, and not the general f(x). . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 30 / 36
- 73. Outline The linear approximation of a function near a point Examples Questions Differentials Using differentials to estimate error Advanced Examples . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 31 / 36
- 74. Gravitation Pencils down! Example Drop a 1 kg ball off the roof of the Silver Center (50m high). We usually say that a falling object feels a force F = −mg from gravity. . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 32 / 36
- 75. Gravitation Pencils down! Example Drop a 1 kg ball off the roof of the Silver Center (50m high). We usually say that a falling object feels a force F = −mg from gravity. In fact, the force felt is GMm F(r) = − , r2 where M is the mass of the earth and r is the distance from the center of the earth to the object. G is a constant. GMm At r = re the force really is F(re ) = = −mg. r2 e What is the maximum error in replacing the actual force felt at the top of the building F(re + ∆r) by the force felt at ground level F(re )? The relative error? The percentage error? . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 32 / 36
- 76. Gravitation Solution Solution We wonder if ∆F = F(re + ∆r) − F(re ) is small. Using a linear approximation, dF GMm ∆F ≈ dF = dr = 2 3 dr dr re re ( ) GMm dr ∆r = 2 = 2mg re re re ∆F ∆r The relative error is ≈ −2 F re re = 6378.1 km. If ∆r = 50 m, ∆F ∆r 50 ≈ −2 = −2 = −1.56 × 10−5 = −0.00156% F re 6378100 . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 33 / 36
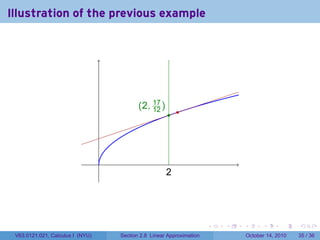
- 77. Systematic linear approximation √ √ 2 is irrational, but 9/4 is rational and 9/4 is close to 2. . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 34 / 36
- 78. Systematic linear approximation √ √ 2 is irrational, but 9/4 is rational and 9/4 is close to 2. So √ √ √ 1 17 2 = 9/4 − 1/4 ≈ 9/4 + (−1/4) = 2(3/2) 12 . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 34 / 36
- 79. Systematic linear approximation √ √ 2 is irrational, but 9/4 is rational and 9/4 is close to 2. So √ √ √ 1 17 2 = 9/4 − 1/4 ≈ 9/4 + (−1/4) = 2(3/2) 12 This is a better approximation since (17/12)2 = 289/144 . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 34 / 36
- 80. Systematic linear approximation √ √ 2 is irrational, but 9/4 is rational and 9/4 is close to 2. So √ √ √ 1 17 2 = 9/4 − 1/4 ≈ 9/4 + (−1/4) = 2(3/2) 12 This is a better approximation since (17/12)2 = 289/144 Do it again! √ √ √ 1 2 = 289/144 − 1/144 ≈ 289/144 + (−1/144) = 577/408 2(17/12) ( )2 577 332, 929 1 Now = which is away from 2. 408 166, 464 166, 464 . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 34 / 36
- 81. Illustration of the previous example . . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 35 / 36
- 82. Illustration of the previous example . . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 35 / 36
- 83. Illustration of the previous example . 2 . . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 35 / 36
- 84. Illustration of the previous example . . 2 . . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 35 / 36
- 85. Illustration of the previous example . . 2 . . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 35 / 36
- 86. Illustration of the previous example . 2, 17 ) ( 12 . . . 2 . . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 35 / 36
- 87. Illustration of the previous example . 2, 17 ) ( 12 . . . 2 . . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 35 / 36
- 88. Illustration of the previous example . . 2, 17/12) ( . . 4, 3) (9 2 . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 35 / 36
- 89. Illustration of the previous example . . 2, 17/12) ( .. ( . 9, 3) ( )4 2 289 17 . 144 , 12 . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 35 / 36
- 90. Illustration of the previous example . . 2, 17/12) ( .. ( . 9, 3) ( ( 577 ) )4 2 . 2, 408 289 17 . 144 , 12 . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 35 / 36
- 91. Summary Linear approximation: If f is differentiable at a, the best linear approximation to f near a is given by Lf,a (x) = f(a) + f′ (a)(x − a) Differentials: If f is differentiable at x, a good approximation to ∆y = f(x + ∆x) − f(x) is dy dy ∆y ≈ dy = · dx = · ∆x dx dx Don’t buy plywood from me. . . . . . . V63.0121.021, Calculus I (NYU) Section 2.8 Linear Approximation October 14, 2010 36 / 36