Module 4 exponential and logarithmic functions

Module 4
Logarithmic Functions
What this module is about
This module deals with the definition, graph, properties, laws and
application of the laws of the logarithmic function; and how to solve simple
logarithmic equation. As you go over the discussion and exercises, you will
appreciate the importance of this function. Find enjoyment in learning this module
and go over the discussion and examples if you have not yet mastered a
concept.
What you are expected to learn
This module is designed for you to:
1. define the logarithmic function f(x) = logax as the inverse of the
exponential function f(x) = ax
,
2. draw the graph of the logarithmic function f(x) = logax,
3. describe some properties of the logarithmic function from its graph;
4. apply the laws of logarithms; and
5. solve simple logarithmic equations.
How much do you know
1. What is the inverse of the exponential function?
a. Linear function
b. Quadratic function
c. Polynomial function
d. Logarithmic function
2. Which of the following is equivalent to log216 = 4?
a. 24
= 16
b. 42
= 16
c. 162
= 4
d. 164
= 2
2. Which of the following is equivalent to ( )3
1
125 = 5?
a. log1255 = 3
1
b. log5125 = 3
1
c. log 3
1 5 = 125
d. log5 3
1
= 125

4. The graph of y = log5x is asymptotic with which of the following lines?
a. y = x
b. x - axis
c. y - axis
d. y = 1
5. The graphs of y = 10x
and y = log10x are symmetric with respect to what
line?
a. y = x + 1
b. y = 2x
c. y = x
d. y = 2x
6. What is the point common to the graphs of functions in the form y = logax?
a. (0, 0)
b. (1, 1)
c. (0, 1)
d. (1, 0)
7. Write log3x2
+ log3y3
– log3z as a single logarithm.
a. log3 






 •
z
yx 32
b. log3(x2
+ y3
- z)
c. log3 






 +
z
yx 32
d. none of the above
8. Simplify log318 + log32 – log34 as a single number.
a. 16
b. 9
c. 3
d. 2
9. Given: log102 = 0.3010, log103 = 0.4771, and log105 = 0.6990, what is log10
1.2?
a. 0.2054
b. 0.0791
c. 1.1132
d. -0.5553
10. Determine the value of x if log7x = - 2.
a. 14
b.
14
1
c. 49
d.
49
1
What you will do
Lesson 1
Logarithmic Function
In the previous module, you have learned about inverse functions. Recall
that when the domain of one function is the range and the range is the domain of
the other then they are inverses. Remember also that to determine the inverse of

a function given an equation you have to interchange x and y then solve for y.
Look at the illustration below on how to find the inverse of the exponential
function, y = ax
.
Exponential Function Inverse function
y = ax
x = ay
You will notice that the inverse of the exponential function shows that “y is
the exponent to which the base a is raised in order to obtain the power x”.
The inverse of the exponential function above is called logarithmic
function. The function is defined by the equation -
x = ay
or y = logax (a>0, a ≠ 1, x > 0)
The equation of a logarithmic function is read as “y is the logarithm of x to the
base a”. Take note that in the notation, a is the base, x is the power and y is the
exponent to which a is raised in order to obtain x.
Example 1. The logarithmic equation 2 = log749 is read as “2 is the logarithm of
49 to the base 7” or “the logarithm of 49 to the base 7 is 2” which
means that the exponent of 7 in order to get 49 is 2.
Example 2. The logarithmic equation log6108 = 3 is read as “the logarithm of 108
to the base 6 is 3” or “3 is the logarithm of 108 to the to the base 6”
meaning the exponent of 6 is 3 to get 108.
Notice from the notation above that y = logax is equivalent to x = ay
. Thus,
an equation in exponential form can be expressed in logarithmic form and vice-
versa. Study the examples that follow.
Example 3. Transform the following equations in logarithmic form.
1. 26
= 64 2.
9
1
3 2-
= 3. ( ) 2128 7
1
=
Solutions:
1. In 26
= 64, the base is 2, the exponent is 6 and the power is 64.
Thus, 26
= 64 is equivalent to 6 = log264 or log264 = 6.
Exponent
Base
Power

2. In
9
1
3 2-
= , the base is 3, the exponent in -2 and the power is
9
1
.
Hence,
9
1
3 2-
= is equivalent to -2 =
9
1
log3 or
9
1
log3 = -2.
.
3. In ( ) 2128 7
1
= , the base is 128, the exponent is
7
1
and the power is 2.
Therefore,( ) 2128 7
1
= is equivalent to
7
1
= log1282 or log1282 =
7
1
.
Example 4. Transform the following logarithmic equations to exponential form.
1. log51 = 0 2. log10.0001 = -4 3. logca = -b
Solutions:
1. In log51 = 0, the base is 5, the exponent is 0, and the power is 1.
Therefore, log51 = 0 is equivalent to 50
= 1.
2. In log100.0001 = -4, the base is 10, the exponent is -4, and the power is
0.0001. Thus, log100.0001 = -4 is equivalent to 10-4
= 0.0001.
3. In logca = -b, the base is c, the exponent is -b, and the power is a. Hence,
logca = -b is equivalent to c-b
= a.
Logarithms can be obtained by considering the corresponding exponential
form of the expression.
Example 5. Evaluate the logarithms of the following:
1. log464 2. log927 3.
625
1
log5
Solutions:
1. Let log464 = x. Transform it in exponential form then solve for x.
4x
= 64
4x
= 43
x = 3
∴log464 = 3
2. Let log927 = x. Transform it in exponential form then solve for x.
log927 = x
9x
= 27
(32
)x
= 33

32x
= 33
2x = 3
2
3
x =
∴ log927 =
2
3
3. Let
625
1
log5
= x. Transform it in exponential form then solve for x.
625
1
log5
= x
5x
=
625
1
5x
= 5-4
x = -4
∴
625
1
log5
= -4
Try this out
A. Write the equivalent exponential form of the following.
1. log232 = 5
2. log381 = 4
3. log1212 = 1
4. log 10100000 = 5
5. log1/5125 = -3
6. log464 = 3
7. log2
16
1 = -4
8. logrt = p
9. logap = s
10.logqp = m
B. Write the equivalent logarithmic form.
1. 35
=243
2. 90
= 1
3. 112
= 121
4. ( ) ( )81
164
3
2
=
5. ( ) 3
4
9
16 2
1
=
6. 36
12
6 =−
7. a-5
= 5
a
1
8. 4=162
1
9. 1252/3
= 25
10.642/3
= 16
C. Evaluate the logarithm of each of the following
1. log981
2. log2128
3. log7343
4. log25625
5. log81
6. log48
7. log644
8. 216
1
6log
9. log4 256
1
10. 5
8 64log

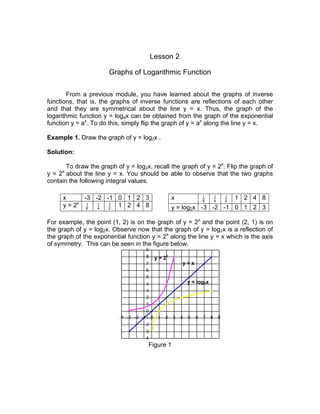
Lesson 2
Graphs of Logarithmic Function
From a previous module, you have learned about the graphs of inverse
functions, that is, the graphs of inverse functions are reflections of each other
and that they are symmetrical about the line y = x. Thus, the graph of the
logarithmic function y = logax can be obtained from the graph of the exponential
function y = ax
. To do this, simply flip the graph of y = ax
along the line y = x.
Example 1. Draw the graph of y = log2x .
Solution:
To draw the graph of y = log2x, recall the graph of y = 2x
. Flip the graph of
y = 2x
about the line y = x. You should be able to observe that the two graphs
contain the following integral values.
For example, the point (1, 2) is on the graph of y = 2x
and the point (2, 1) is on
the graph of y = log2x. Observe now that the graph of y = log2x is a reflection of
the graph of the exponential function y = 2x
along the line y = x which is the axis
of symmetry. This can be seen in the figure below.
Figure 1
x -3 -2 -1 0 1 2 3
y = 2x
8
1
4
1
2
1 1 2 4 8
x 8
1
4
1
2
1 1 2 4 8
y = log2x -3 -2 -1 0 1 2 3
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
9
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9
y = x
y = 2x
y = log2x

-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
9
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9
To draw the graph of y = ( )x
2
1
and its inverse y = log
2
1 x, follow the steps in
the previous example, that is, draw the graph of y = ( )x
2
1
then flip it along the line
y = x. Observe that the graph of y = log
2
1 x contain the following integral values
shown below.
Figure 2
Notice that just like in Figure 1, the graph of y = log
2
1 x is a reflection of the
graph of y = ( )x
2
1
. The two graphs are also symmetrical about the line y = x.
Try this out
A. Sketch the graph of each of the following logarithmic functions using the
graph of its inverse.
1. f(x) = log3x
2. f(x) = log4x
3. f(x) = log5x
4. f(x) = log1/3x
5. f(x) = log1/4x
6. f(x) = log1/5x
B. Compare and contrast the graphs of numbers 1 and 4, numbers 2 and 5,
and numbers 3 and 6.
x -3 -2 -1 0 1 2 3
y = 2x
8 4 2 1 2
1
4
1
8
1
x 8 4 2 1 2
1
4
1
8
1
y = log2x -3 -2 -1 0 1 2 3
y = x
y = ( )x
2
1
y = log
2
1 x

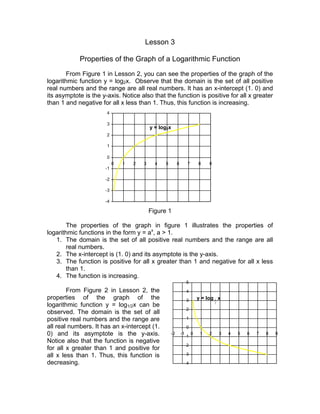
-4
-3
-2
-1
0
1
2
3
4
5
-2 -1 0 1 2 3 4 5 6 7 8 9
Lesson 3
Properties of the Graph of a Logarithmic Function
From Figure 1 in Lesson 2, you can see the properties of the graph of the
logarithmic function y = log2x. Observe that the domain is the set of all positive
real numbers and the range are all real numbers. It has an x-intercept (1. 0) and
its asymptote is the y-axis. Notice also that the function is positive for all x greater
than 1 and negative for all x less than 1. Thus, this function is increasing.
Figure 1
The properties of the graph in figure 1 illustrates the properties of
logarithmic functions in the form y = ax
, a > 1.
1. The domain is the set of all positive real numbers and the range are all
real numbers.
2. The x-intercept is (1. 0) and its asymptote is the y-axis.
3. The function is positive for all x greater than 1 and negative for all x less
than 1.
4. The function is increasing.
From Figure 2 in Lesson 2, the
properties of the graph of the
logarithmic function y = log1/2x can be
observed. The domain is the set of all
positive real numbers and the range are
all real numbers. It has an x-intercept (1.
0) and its asymptote is the y-axis.
Notice also that the function is negative
for all x greater than 1 and positive for
all x less than 1. Thus, this function is
decreasing.
-4
-3
-2
-1
0
1
2
3
4
0 1 2 3 4 5 6 7 8 9
y = log2x
y = log
2
1 x

The properties of the graph in figure 1 illustrates the following properties of
logarithmic functions in the form y = ax
, 0 < a < 1.
1. The domain is the set of all positive real numbers and the range are all
real numbers.
2. The x-intercept is (1. 0) and its asymptote is the y-axis.
3. The function is negative for all x greater than 1 and positive for all x less
than 1.
4. The function is decreasing.
Try this out
A. Enumerate the properties of the graphs of the following logarithmic functions.
Refer to the graphs drawn in Lesson 2.
1. f(x) = log3x
2. f(x) = log4x
3. f(x) = log5x
4. f(x) = log1/3x
5. f(x) = log1/4x
6. f(x) = log1/5x
B. Give the properties common to the graphs in A.
Lesson 4
Laws of Logarithms
Since logarithmic function and exponential function are inverse functions,
the laws of exponents will be used to derive the laws of logarithms. The laws of
logarithms were important tools in shortening complicated computations long
before the use of scientific calculators and computers. Nowadays, logarithms are
used for different purposes specifically in sciences.
A. The Logarithm of a Product
Let M = ax
and N = ay
.
By Law of Exponents for Products, MN = ax
•ay
= ax + y
.
By definition of logarithmic function,
M = ax
↔ logaM = x,
N = ay
↔ logaN = y, and

MN = ax + y
↔ logaMN = x + y.
By substitution, logaMN = logaM + logaN.
From the derivation, the logarithm of the product of two numbers is the
sum of the logarithms of the two factors.
B. The Logarithm of a Quotient
Use the given in A and the Law of Exponents for Quotients, y-x
y
x
a
a
a
N
M
== .
M = ax
↔ logaM = x,
N = ay
↔ logaN = y, and
y-x
a
N
M
= ↔ y-x
N
Mloga =





By substitution, NlogMlog
N
Mlog aaa -=





From the derivation, the logarithm of the quotient of two numbers is the
difference of the logarithms of the dividend and the divisor.
C. The logarithm of a Power
Let M = ax
.
By the Law of Exponents for a Power, Mk
= (ax
)k
.
M = ax
↔ logaM = x, and
Mk
= (ax
)k
↔ logaMk
= xk.
By substitution, logaMk
= klogaM
From the derivation, the logarithm of the kth
power of a number is k times
the logarithm of the number.
Below are examples of the application of the laws of logarithms.
Example 1. Simplify the following using the laws of logarithms.
1. loga5PQ
2. 





5
32loga
3. logb(24)3
4. logb 3
7
y
x

Solutions:
1. Apply the logarithm of a product.
loga5PQ = loga5 + logaP + logaQ
2. Apply the logarithm of a quotient.






5
32loga = loga32 – loga5
3. Apply the logarithm of a power.
logb(24)3
= 3logb24
4. Apply the logarithm of a power and logarithm of a quotient and
distributive property.
logb 3
7
y
x =
3
1
7
y
xlogb 







= 







y
xlog
7
b
3
1
=
3
1
( logbx7
– logby)
=
3
1
logbx7
-
3
1
logby
=
3
1
(7logbx) -
3
1
logby
=
3
7
logbx -
3
1
logby
Example 2: Write the following as a single logarithm. Simplify if possible.
1. log412p + 9log4q
2. logd(h2
– 16) – log4(h + 4)
Solution:
1. The expression is an application of the logarithm of a power and
logarithm of a product.
log412p + 9log4q = log412p + log4q9
= log4(12pq9
)
2. The expression is an application of the logarithm of a quotient.
logd(h2
– 16) – logd(h + 4) = 







+ 4h
16-hlog
2
d

=








+
+
4h
4)4)(h-h(
logd
= logd(h – 4)
Example 3: Given that log 2 = 0.3010, log 3 = 0.4771, and log 5 = 0.6990,
determine-
1. log 15
2. log 0.4
3. log 3.6
4. log 4
625
5.
2
30
log
3
Solution:
Observe that no base was indicated in example 3. When no base is
indicated, it means that the base is 10. By convention, when base 10 is used we
write log x instead of log10x. We call this common logarithm. Thus, we will use
this convention from now on.
1. log 15 = log (3•5) = log 3 + log 5 = 0.4771 + 0.6990 = 1.1761
2. log 0.6 =
5
3log = log 3 – log 5 = 0.4771 – 0.6990 = -0.2219
3. log 3.6 =
5
18
log
=
5
32
log
2
•
= log 2 + log 32
– log 5
= log 2 + 2log3 – log 5
= 0.3010 + 2(0.4771) – 0.6990
= 0.3010 + 0.9542 – 0.6990
= 0.5562
4. log 4
625 = ( )4
1
125log
= log( )4
1
3
5
= 4
3
5log
= 5log
4
3
= ( )6990.0
4
3
= 0.52425

5.
2
30
log
3
= 2log-30log3
= ( ) 2log532log -3
1
••
= 2log-)5log3log2(log
3
1
++
= 0.3010-)6990.04771.03010.0(
3
1
++
= 3010.0)4771.1(
3
1
−
= 0.4924 – 0.3010
= 0.1914
Try this out
A. Express the following as a single logarithm and simplify:
1. log2192 + log26
2. log336 + log34 – log316
3. log5
3
625
4. log798 + 2log77 – log72
5. 2log-18log27log
6
1
333 +
6. log2x + 3 log2y – log2z
7. log (3x2
+ 11x – 20) – log (3x – 4)
8. logb(2x -5) + logb(x + 1)
9. 2logax3
+ 3logay + 4logaz - 3logaw
10. )2xlog(3)4-xlog(
2
1 2
++
B. Given log 3 = 0.4771, log 5 = 0.6990, and log 7 = 0.8451, evaluate the
following applying the laws of logarithms:
1. log 21
2. log 63
3. log 4.2
4. log 492
5. 4
45log
6.
7
75
ogl
7.
9
49
log
8.
5
2175
log
4
9.
( )
27
21
log
2
10.
5
147
log

C. If z = log 5, write the following expressions in terms of z:
1. log 25
2. log56
3.
125
1
log
4. log 25
5. log 5000
Lesson 5
Logarithmic Equations
Logarithmic equations are equations involving logarithmic functions.
From previous lesson, you learned that exponential functions and
logarithmic functions are inverses. Hence, the properties of these functions can
be used to solve equations involving these two functions.
Study the following examples illustrating how logarithmic equations are
solved.
Example 1: Solve the missing terms in the following logarithmic equations.
1. log6216 = x
2. logx81 =
3
2
3. log25x =
2
3
4. log4(5x + 4) = 3
5. log (2x2
+ 4x – 3) = log (x2
+ 2x + 12)
Solutions:
1. Transform log6216 = x in exponential form, then solve for x.
6x
= 216
6x
= 63
x = 3
Check:
If x = 3, then 63
= 216.
∴log6216 = 3 and x = 3.
2. Transform logx81 =
3
2
in exponential form, then solve for x using the
properties of exponents.
81x3
2
=

4
3x3
2
=
( )2
32
3
3
2
4
3x =




 Raise both sides to the same power and
x = 36
simplify
x = 729
Check:
If x = 729, then ( ) 8133729 46 3
2
3
2
=== .
∴x = 729.
3. Transform log25x =
2
3
in exponential form, then solve for x using the
properties of exponents.
2
3
25x=
( )2
3
2
5x=
x = 53
x = 125
Check:
25 2
3
= ( ) 12555 32 2
3
==
∴ x = 125.
4. Transform log4(5x + 4) = 3 in exponential form, then solve for x.
5x + 4 = 43
5x + 4 = 64
5x = 64 – 4
5x = 60
12
60
x=
x = 5
Check:
If x = 5, then log4[5(12) + 4] = log4(60 + 4) = log464 = 3.
∴ x = 5
5. log (2x2
- 7x – 9) = log (x2
- 9x + 6)
Since both sides of the equation are in base 10, then
2x2
- 7x – 9 = x2
- 9x + 6
2x2
- 7x – 9 – (x2
- 9x + 6) = 0 Addition Property of Equality
x2
+ 2x - 15 = 0 Simplify
(x + 5)(x - 3) = 0 Factoring
x + 5 = 0 or x - 3 = 0
x = -5 or x = 3

Check:
If x = -5, then log (2x2
- 7x – 9) = log [2(-5)2
- 7(-5) – 9]
= log [2(25) + 35 – 9]
= log (50 + 35 – 9)
= log 76
and log (x2
- 9x + 6) = log [(-5)2
- 9(-5) + 6]
= log (25 + 45 + 6)
= log 76.
Hence, x = -5 is a solution
If x = 3, then log5 log (2x2
- 7x – 9) = log [2(3)2
- 7(3) – 9]
= log [2(9) – 21 – 9]
= log (18 – 21 – 9)
= log (-12)
Hence, x = 3 is not a root since logarithms is defined only for positive
number.
∴x = -5 is the only solution.
Notice that to solve problems 1 to 4 the logarithmic equations were first
transformed to exponential form.
Example 2: Solve for x in the following exponential equations:
1. 5x
= 9 2. 3x + 7
= 2x
Solutions:
Exponential equations involving different bases can be solved with the
use of logarithms and the aid of a scientific calculator or a table of
logarithms. In the case of the example 2, a scientific calculator will be used.
1. 5x
= 9
log 5x
= log 9 Get the logarithm of both sides.
xlog 5 = log 9 Logarithm of a Power
5log
9log
x= Multiplication Property of Equality
6990.0
9542.0
x = Replacement of value from the table or
calculator
x = 1.3651 Division Fact
Check:
Using a scientific calculator,
51.3651
= 9 (rounded to the nearest whole number)

2. 3x + 2
= 2x
log 3x + 2
= log 2x
Get the logarithm of both sides
(x + 2)log 3 = x log 2 Logarithm of a Power
x log 3 +log 3 = x log 2 Distributive Property
x log 3 – x log 2 = -2log 3 Addition Property of Equality
x(log 3 – log 2) = -2log 3 Factoring
2log-3log
3log2
x
−
= Multiplication Property of Equality
0.3010-0.4771
2(0.4771)-
x = Replacement of value from the table or
calculator
1761.
9542.0
x
−
= Multiplication Fact
x = -5.4185 Division Fact
Check:
Using a scientific calculator,
3-5.4185 + 2
= 2-5.4185
3-3.4185
= 2-5.4185
0.0234 = 0.0234
Try this out
A. Solve for the missing term:
1. log7n = -3
2. log4512 = x
3. logc36 = -2
4. log25r =
2
7
5. logp256 = -7
6. log8128 = y
7. log x - log 12 = 3
8. log5x5
- log5x3
= 2
9. log p – log 3 = 1
10. log2z + log22z = 3
11. log7a + log7(a - 1) = log712
12. log3y – log3(y – 2) = log32
13. log x + log (x + 1) = log 20
14. log (3x – 5) + log 2x = log 4
15. log 25x – log 5 = 2
16. log3(x2
– 16) – log3(x + 4) = 2
17. log5(m + 5) – l0g5(m + 1) = log54
18. log7(q + 4) – log73 = log7(q – 4)
19. log (14v2
+ 35v) = log 3 + log (2v + 5)

20. log (21h2
+ 50h – 14) = log(3h2
+ 25h + 14)
B. Solve the following exponential equations using logarithms:
1. 4x
= 5
2. 32x
= 18
3. 5x
+ 1 = 9
4. 5x – 2
= 4x – 1
5. 23x + 5
= 3x
Let’s Summarize
1. The inverse of the exponential function above is called logarithmic
function. The function is defined by the equation,
x = ay
or y = logax (a>0, a ≠ 1, x > 0)
read as “y is the logarithm of x to the base a” where a is the base, x is
the power and y is the exponent to which a is raised in order to obtain x.
2. The graph of the logarithmic function y = logax can be obtained from the
graph of the exponential function y = ax
. To do this, flip the graph of y = ax
along the line y = x.
3. The properties of the graph logarithmic functions in the form y = ax
, a > 1
are as follow:
a. The domain is the set of all positive real numbers and the range are all
real numbers.
b. The x-intercept is (1. 0) and its asymptote is the y-axis.
c. The function is positive for all x greater than 1 and negative for all x
less than 1.
d. The function is increasing.
4. The properties of the graph of logarithmic functions in the form y = ax
,
0 < a < 1are as follow:
a. The domain is the set of all positive real numbers and the range are all
real numbers.
b. The x-intercept is (1. 0) and its asymptote is the y-axis.
c. The function is negative for all x greater than 1 and positive for all x
less than 1.
d. The function is decreasing.

5. The Law of Logarithms are as follows:
a. Logarithm of a Product: logaMN = logaM + logaN
b. Logarithm of a Quotient: NlogMlog
N
Mlog aaa -=





c. Logarithm of a Power: logaMk
= klogaM
6. To solve simple logarithmic equations, transform the equation in
exponential form, then solve for the missing term.
7. To solve exponential equations involving different bases, find the
logarithm of both sides of the equation with the aid of a scientific calculator
or a table of logarithms then solve for the missing term applying the
properties of equality.
What have you learned
1. Which of the following is the inverse of y = ax
?
a. y = ax
b. y = xa
c. y = logax
d. a = yx
2. Which of the following is equivalent to log464 = 3?
a. 34
= 64
b. 43
= 64
c. 644
= 3
d. 163
= 4
3. Which of the following is equivalent to ( )3
1
27 = 3?
a. log273 = 3
1
b. log327 = 3
1
c. log 3
1 3 = 27
d. log3 3
1
= 27
4. At what point does the graph of y = log2x intersect the x-axis?
a. (0, 1)
b. (0, 0)
c. (-1, 0)
d. (1, 0)
5. The graphs of y = 4x
and y = log4x are symmetric with respect to what
line?
a. y = x + 1
b. y = 4x
c. y = x
d. y = 4x
6. What is the point common to the graphs of functions y = log3x and
y = log10x?
a. (0, 0)
b. (1, 1)
c. (0, 1)
d. (1, 0)

7. Write 3 log a + 5 log b – 4 log c as a single logarithm.
a. log 






 •
4
53
c
ba
b. log (a3
+ b5
– c4
)
c. log 






 +
4
53
c
ba
d. none of the above
8. Simplify log381 + log33 – log39 as a single number.
a. 27
b. 5
c. 3
d. 2
9. Given that log102 = 0.3010, log103 = 0.4771, and log105 = 0.6990, what is
log 107.5?
a. 0.5229
b. 0.0791
c. 0.8751
d. 1.4471
10. Determine the value of x if log5 (8x - 7) = 2
a. 4.875
b. 4
c. 3.125
d. 2.25

Answer Key
How much do you know
1. d
2. a
3. a
4. c
5. c
6. d
7. a
8. d
9. b
10. d
Try this out
Lesson 1
A. 1. 25
= 32
2. 34
= 81
3. 121
= 12
4. 105
= 100000
5. 125
5
1
3
=





−
6. 43
= 64
7. 2-4
=
16
1
8. rp
= t
9. as
= p
10. qm
= p
B. 1. log3243 = 5
2. log91 = 0
3. log11121 = 2
4. 4
81
16
log
3
2 =
5.
2
1
3
4
log
9
16 =
6. 2
36
1
log6 −=
7. 5
a
1
log 5a −=
8.
2
1
4log16 =

9.
3
2
25log125 =
10.
3
2
16log64 =
C. 1. 2
2. 7
3. 3
4. 2
5. 0
6.
2
3
7.
3
1
8. -3
9. -4
10.
5
2
Lesson 2
A.
-6
-4
-2
0
2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
-2 0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30
1. y = log3x
y = 3x

-4
-2
0
2
4
6
8
10
12
14
16
18
-4 -2 0 2 4 6 8 10 12 14 16 18 20
-5
0
5
10
15
20
25
30
-5 0 5 10 15 20 25 30
-6
-3
0
3
6
9
12
15
18
21
24
27
30
-6 -3 0 3 6 9 12 15 18 21 24 27 30
2. y = log4x
3. y = log5x
y = 4x
y = 5x
y =
x
3
1






4. y = xlog
3
1

-4
-2
0
2
4
6
8
10
12
14
16
18
-4 -2 0 2 4 6 8 10 12 14 16 18
-4
-2
0
2
4
6
8
10
12
14
16
18
20
22
24
26
28
-4 -2 0 2 4 6 8 10 12 14 16 18 20 22 24 26 28
B. The graph of y = log3x has the same shape and size as the graph of
xlogy
3
1= . The same is true for the graphs of y = log4x and xlogy
4
1= ,
and y = log5x and xlogy
5
1= . The graphs of y = log3x, y = log4x and
y = log5x are increasing while the graphs of xlogy
3
1= , xlogy
4
1= , and
y=
x
4
1






5. y = xlog
4
1
y =
x
5
1






6. y= xlog
5
1

xlogy
5
1= are decreasing. The six graphs have a common point (1, 0).
Lesson 3
A.
B. Common Properties: Domain, range, x-intercepts, and asymptotes.
Lesson 4
A.
1. log232 = 5
2. log39 = 2
3.
3
4
log55=
3
4
4. 4log77 = 4
5.
2
5
log33 =
2
5
6. log
z
xy3
2
7. log (x+ 5)
8. logb(2x2
– 3x – 5)
9. log 3
436
a
w
zyx
10.log 32
)2x(4x +−
B.
1. 1.3222
2. 1.7993
3. 0.6232
4. 3.3804
5. 0.4133
6. 1.03
7. -0.1091
8. 1.5066
9. 1.2131
10.1.8178
C.
1. 2z
2. 6z
3. -3z
4. z
5. z + 3
No
.
Equation Domain Range x-intercept Asymptote Trend
1 y = log3x + Real Nos. Real Nos. (1, 0) y-axis increasing
4 xlogy
3
1= + Real Nos. Real Nos. (1, 0) y-axis decreasing
5 xlogy
4
6 xlogy
5

Lesson 5
A.
1.
343
1
2.
2
9
3.
6
1
4. 78125
5.
2
1
6.
3
7
7. 12000
8. 5
9. 30
10.2
11.4
12.4
13.4
14.2
15.20
16.13
17.
3
1
18.8
19.
7
3
20.3
B.
1. 1.16
2. 1.32
3. 1.29
4. 8.21
5. -3.53
What have you learned
1. c
2. b
3. a
4. d
5. c
6. d
7. a
8. c
9. c
10. b

Module 4 exponential and logarithmic functions

More Related Content

What's hot (20)

Viewers also liked (20)

Similar to Module 4 exponential and logarithmic functions (20)

More from dionesioable (20)

Recently uploaded (20)

Module 4 exponential and logarithmic functions