Nonlinear Beam theory

1
Presentation On
STUDY OF
“HIGHER ORDER SHEAR DEFORMATION BEAM
THEORY”
STRUCTURAL ENGINEERING
DEPARTMENT OF CIVIL ENGINEERING
SUBMITTED BY
Robin Jain

• Beam theory is a simplification of the linear theory of
elasticity which provides a means of calculating the load-
carrying and deflection characteristics of beams.
• Beam is a 3D element, we need to calculate the resisting
moment capacity of the beam, for which we have to find
the stress at various points in the beam.
• Strain is the quantity which we can find and then stress can
be calculated.
BEAM THEORY

• Analyzing a 3D beam is tedious needs to be calculate in less
dimensions for simplified analysis.

BASIC ASSUMPTIONS
• Let us assume that the loading is uniform and similar
across width ( That may be practically incorrect).
As ‘x-dimension’ is so high compare to ‘y’ and ‘z’
dimensions.
• Now we have a planer beam element, and width becomes
just a multiplier ( the effect of loading, through out the
width will uniform)

• To convert the beam into single dimension, depth should
neglect. For this the strain distribution through out the
depth has to be identify and solved.
• Various theories have been given by researchers,
Above neutral axis, beam is in ‘compression’ and below
neutral axis, beam is in ‘Tension’

Single order shear deformation beam theory
• Euler–Bernoulli beam theory (1750)
• Rayleigh theory (1877)
• Timoshenko beam theory (20th century)
Classical beam theory predicts stiffer response for laminated
composite beams with moderate length to thickness ratio
because no shear deformation is allowed for in this theory..
Timoshenko First-order shear deformation beam theory
(FSDBT) is first developed to account for shear deformation
with the assumption that the displacement in the beam
thickness direction does not restrict cross section to remain
perpendicular to the deformed centroidal line.

EULER-BERNOULLI BEAM THEORY
Assumptions:
• Cross-sections which are plane & normal to the
longitudinal axis remain plane and normal to it after
deformation.
• If we take a element as shown in diagram then it will
remain square, that means no shear deformation is there
in beam.
Shear Deformations are neglected.
• Beam Deflections are small.

Displacements –
• ux(x,z) = -zw’(x) , uy= 0 , uz (x,z) = w(x)
Associated strains –
εx (x,z) = ux,x = -zw”(x), 2εxz = ux,z + uz,x = 0

Euler-Bernoulli eq. for bending of Isotropic beams of
constant cross-section:
EI
𝑑4
𝑊(𝑋)
𝑑𝑋4 =q(x)
where:
w(x): deflection of the neutral axis
q(x): the applied transverse load

TIMOSHENKO BEAM THEORY
Assumptions:
• Plane section before bending remains plane after bending.
• Cross section which are normal to longitudinal axis will not
be remain normal to it after bending.
• If we take a element as shown in diagram then it will
turned to be rhombus, that means shear deformation is
there in beam.

Displacements –
ux(x,z)=zø(x), uy=0 ,uz=w(x)
Associated strains –
εx (x,z) = zø(x),2εxz =ø(x)+w’(x)

Shear Correction Factor (K) :-
Timoshenko Defined it as:
K =
𝐴𝑣𝑒𝑟𝑎𝑔𝑒 𝑠ℎ𝑒𝑎𝑟 𝑠𝑡𝑟𝑎𝑖𝑛 𝑜𝑛 𝑎 𝑠𝑒𝑐𝑡𝑖𝑜𝑛
𝑆ℎ𝑒𝑎𝑟 𝑠𝑡𝑟𝑎𝑖𝑛 𝑎𝑡 𝑡ℎ𝑒 𝑐𝑒𝑛𝑡𝑟𝑜𝑖𝑑
Significance of Shear Correction Factor K :
Multilayered plate and Shell finite elements have a constant
shear distribution across thickness. This causes a
decrease in accuracy
especially for sandwich structures. This problem is overcome
using shear correction factors .

• Basic difference from Euler-Bernoulli beam theory is
that Timoshenko beam theory considers the effects of
Shear and also of Rotational Inertia in the Beam
Equation. So physically, Timoshenko’s theory effectively
lowers the stiffness of beam and the result is a larger
deflection.
• Timoshenko’s eq. for bending of Isotropic beams of
constant cross-section:
EI
𝑑4
𝑊(𝑋)
𝑑𝑋4 =q(x) -
𝐸𝐼
𝐾𝐴𝐺
𝑑4
𝑞
𝑑𝑥2
Where:
A:Area of cross section
G: Shear Modulus
K: Shear correction factor

NEED OF HIGHER ORDER SHEAR DEFORMATION BEAM
THEORIES
• the shear stress-free boundary conditions on the top and
bottom beam surfaces are not satisfied in the first-order shear
deformation theory so a shear correction factor is needed to
correct the Discrepancy in shear force of the first-order shear
deformation theory and the three-dimensional elasticity
theory. In order to overcome this drawback, some higher-
order shear deformation theories have been developed by a
few researchers. All these proposed theories differ mainly in
the inclusion of the shear Deformation effect in their
kinematics formulations.

• As far as these theories are single order shear deformation,
so are not accurate as strain variation across depth is not
linear and also sometimes shear deformation can not be
neglected. Hence there were requirement to develop
‘Higher order shear deformation beam theory’.
• The First order shear deformation beam theory have been
used extensively but when is applied to composite beam,
the difficulty in accurately evaluating the shear correction
factors present the shortcoming of First order shear
deformation theory, because the higher-order polynomial
in the thickness direction of beam could be able to
approximate the nonlinear distribution of transverse shear
stress and the corresponding theories avoid to use the
single deformation corrector like in first order theories.

• The shear deformation effects are more pronounced in the
thick beams than in the slender beams. These effects are
neglected in elementary theory of beam (ETB) bending. In
order to describe the correct bending behavior of thick
beams including shear deformation effects and the
associated cross sectional warping, shear deformation
theories are required. This can be accomplished by
selection of proper kinematics and constitutive models.
The functions f(z) is included in the displacement field of
higher order theories to take into account effect of
transverse shear deformation and to get the zero shear
stress conditions at top and bottom surfaces of the beam.

ASSUMPTIONS OF HIGHER ORDER BEAM THEORY
• Reﬁned higher order beam theories were introduced, in
which it is assumed that the cross sections behave each as
a lamina capable to warp according to a suitably speciﬁed
warping mode. For this purpose, the longitudinal pointe
wise displacement was enriched by one, or more, extra
terms incorporating either polynomial functions of the
transverse co-ordinate.
• Hence the planer section before bending will not remain
plane after bending and also the cross section will not
perpendicular to neutral axis ( Due to consideration of
shear deformation)

WORKS ON HOSD BEAM THEORIES
• Levinson, Bickford, Renfield and murty, Bhimaraddi
and chandrashekhra presented parabolic shear
deformation theories assuming a higher variation of axial
displacement in terms of thickness coordinate. These
theories satisfy shear stress free boundary conditions on
top and bottom surfaces of beams and thus obviate the
need of shear stress correction factor.
• Kant and Gupta, heyliger and Reddy presented finite
element models based on higher order shear
deformation uniform rectangular beams. However, these
displacement based finite element models are not free
from phenomenon of shear locking.

• Vlasao and Leont’ev, Stein developed refined shear
deformations theories for thick beams including
sinusoidal function in terms of thickness coordinate in
displacement field, However, with these theories shear
stress free boundary conditions are not satisfied at top
and bottom surfaces of beam. A study literature by ghugal
and Shimpi indicates that the research work dealing with
flexural analysis of thick beams using refined
trigonometric and hyperbolic shear deformation theories
is very scarce and still in infancy.

• Rectangular beam theory is given by LEVINSON
• Trigonometric shear deformation theories are presented
by TOURATIER, VLASOV and LEONT’ev and STEIN for
thick beams
These theories are not satisfied for shear stress at free
boundaries .
• Trigonometric shear deformation theories given by
GHUGAL and SHIPMI which satisfies the shear stress free
conditions at top and bottom surfaces of beam .
• Hyperbolic shear deformation theory is given by
SOLDATOS

Reddy advanced a refined third order beam theory
• Timoshenko beam model is modified by allowing the cross
sections to warp in a specified warping mode.
• profile of the warped cross section intersects the upper and
lower surfaces orthogonally
ux(x,z) = zϕ(x) -
4z3
3h2 [ϕ(x) + w’(x)] (1)
Leaving unchanged the other displacement components. The
concomitant strain components turn out to be
x (x,z) = zϕ’(x) -
4z3
3h2 [ϕ’(x) + w’’(x)] (2)

These relations show that
• the axial strain xhas a nonlinear (third order)
distribution within the cross section
• the shear strain xzhas there a parabolic distribution with
zero values for z =±h/2. The warping mode that
characterizes the Reddy beam theory is determined by
the third order monomial function g1 (z)=
4z3
3h2 .
Sequence of higher order beams
In this section, Reddy-type beams of (odd) order N=2n+1
are considered and then a sequence of such beams is
constructed by taking n = 0,1,2,…. The limit beams for n = 0
and n = ∞ are shown to coincide with, respectively, the
classical Eulere Bernoulli and Timoshenko beams.
xz(x,z) = 1 −
2z
h
𝟐
ϕ(x)+w’(x) (3)

Generalized higher order beam
The beam theory of Reddy is here generalized by considering a
beam model of any odd order, say N=2n+1, with the integer
n > 0 arbitrarily fixed.
Additionally, as independent kinematic variables
we take the deflection function w(x) and the shear angle
function Y(x) defined as
Y (x)=ϕ(x)+w’(x) xϵ(0,L) (4)

Fig. 1. Schematics of a beam segment in its initial configuration and of its
deformation state at the generic cross section Ω(x) with the slope -w’ of the
deflected axis, the absolute rotation ϕ of the cross section and the shear
angle Y, along with a typical configuration of the warping profile and related
displacements for a generic n.

This function Y(x)gives the sectional intrinsic rotation, that is,
the (anticlockwise) relative rotation of Ω(x) with respect to the
plane normal to the deformed axis, measured at the points of
the neutral axis (Fig. 1).
With these assumptions in mind, the displacements ux,uy,uz are
assumed as
ux(x,z) = - zw’(x)+ [z - gn(z)] Y (x) (5)
uy= 0, uz(x,z) = w(x) (6)
Where gn(z)denotes the(2n+1)thorder warping function
defined as
gn(z) =
z2n+1
(2n+1)(𝒉/𝟐) 𝟐𝒏 (7)

Having the dimension of a length. The curve gn(z) is plotted in
Fig. 2 for a few values of n. A characteristics of the function
gn(z) is that its first derivative at Z=±h/2 is equal to unity for
all n, that is,
𝒅𝐠𝐧(𝐳)
𝒅𝒛 z=±h/2 =1 n=0,1,2,…… (8)
Another characteristics of gn(z) is that its derivatives at z = 0
up to the order 2n are all vanishing, but the analogous
derivative of order 2n +1 is non-zero, namely,
𝐝 𝐤
𝐠 𝐧
(𝐳)
𝐝𝐳 𝒌 z=0= 0 (k=0,1,……2n) (9)
D2n+1gn(z)
dzk z=0 =
𝟏
(h/2)2n (𝟐𝒏)
(10)

PLOTS OF WARPING FUNCTION (DIAGRAM)

Eqs. (8) and (9) imply that the curve gn(z)remains almost flat
within a central part of the thickness, this part being the
wider, the higher is n (hence the smaller is the derivative (10),
then it goes smoothly toward the extremes z = ±h/2, with the
final slopes equal to unity. For n = ∞, the curve gn(z) remains
fully flat for the whole thickness (with zero slope), except for
the infinitesimal upper and lower segments where it exhibits a
slope discontinuity with unit slope values at the ends.
For n = 0, recalling (7) and with the additional assumption
Y(x) ≡ 0, we have
ux = -zw’(x); x= -zw”(x); xz ≡0 (15)

that is, the beam model B0 coincides with the classical
EulereBernoulli beam, see (1) and (2).
For n=1
Ux=zФ(x)-
4z3
3h2Y(x)
xz=zФ’(x ) -
4z3
3h2Y’(x)
2 xz = 𝟏 − (
𝟐𝒛
𝒉
)2 Y(x)
which, complemented by (8)2, state that the beam
modelcoincideswith the beam model advanced by Reddy
(Heyligerand Reddy, 1988; Reddy, 2007), see (5) and (6).
(15)

For n=2, we have:
ux= zФ(x) -
16z5
5h4 Y(x)
xz= zФ(x) -
16z5
5h4 Y’(x)
2 xz= 𝟏 − (
𝟐𝒛
𝒉
)4 Y(x)
(16)
which, complemented by (8)2, state that the beam model B2
is a Reddy-type beam of fifth order. Analogously, the beam
models B3, B4, etc. constitute Reddy-type beams of finite
(odd) order higher than 5.

For n ∞,
we have:
ux= zϕ(x), x = zϕ’(x)
2 xz =
Y (𝒙), 𝒇𝒐𝒓𝒛 < 𝒉/𝟐
𝟎, 𝒇𝒐𝒓 𝒛 =
Eq. (17) together with (6) state that the beam model B∞
can be identified with the classical Timoshenko beam,
(17)

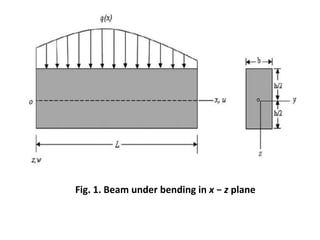
NUMERICAL RESULT
Beam under consideration
Consider a beam made up of isotropic material as shown in Fig. 1.
The beam can have any boundary and loading conditions. The
beam under consideration occupies the region given by
0 ≤ x ≤ L, −b/2 ≤ y ≤ b/2, −h/2 ≤ z ≤ h/2, (1)
where x, y, z are Cartesian co-ordinates, L is length, b is width and
h is the total depth of the beam. The beam is subjected to
transverse load of intensity q(x) per unit length of the beam.

Assumptions made in theoretical formulation
1. The in-plane displacement u in x direction consists of two
parts:
(a) A displacement component analogous to displacement in
elementary beam theory of bending;
(b) Displacement component due to shear deformation which
is assumed to be parabolic, sinusoidal, hyperbolic and
exponential in nature with respect to thickness coordinate
2. The transverse displacement w in z direction is assumed to
be a function of x coordinate.
3. One dimensional constitutive law is used.
4. The beam is subjected to lateral load only.

Fig. 1. Beam under bending in x − z plane

The displacement field
Based on the before mentioned assumptions, the displacement
field of the present unified shear deformation theory is given as
below
u(x,z,t) = -z
𝝏𝒘
𝝏𝒙
+ f(z)ϕ(x,t) (2)
w(x,z,t) = w(x,t) (3)
Here
u = axial displacements of the beam center line in x directions
w = transverse displacements of the beam center line in z
directions
t is the time.

Table 1. Functions f(z) for different shear stress distribution
Model Author Function f(z)
Model 1 (Ambartsumian [2])
f(z)=
𝑧
2
−
ℎ2
4
−
𝑧2
3
Model2 (Kruszewski[15])
f(z)=
5𝑧
4
1 −
4𝑧2
3ℎ2
Model3 (Reddy[18])
f(z)=z 1 −
4
3
𝑧
ℎ
2
Model4 (Touratier[25]) f(z)=
ℎ
𝜋
sin
𝜋𝑧
ℎ
Model5 (Soldatos[22]) f(z)= 𝑧 cosh
1
2
− ℎ sinh
𝑧
ℎ
Model6 (Karama et al.[14])
f(z)=zexp −2
𝑧
ℎ
2
Model7 (Akavci[1]) f(z)=
3𝜋
2
ℎ tanh
𝑧
ℎ
− 𝑧 sec ℎ 2 1
2

Numerical results
The results for transverse displacement (w), axial bending
stress (σx), transverse shear stress (τzx) and fundamental
frequency ωmare presented in the following non-dimensional
form
ῶ =
𝟏𝟎𝑬𝒃𝒉 𝟑 𝒘
𝒒 𝟎 𝑳 𝟒 σ’X=
𝒃𝝈 𝒙
𝒒 𝟎
τ’zx=
𝒃𝝉 𝒛𝒙
𝒒 𝟎
S=
𝑳
𝒉
(4)
where S is the aspect ratio.
Error=
𝒗𝒂𝒍𝒖𝒆 𝒃𝒚 𝒂 𝒑𝒂𝒓𝒕𝒊𝒄𝒖𝒍𝒂𝒓 𝒎𝒐𝒅𝒆𝒍−𝒗𝒂𝒍𝒖𝒆 𝒃𝒚 𝒆𝒙𝒂𝒄𝒕 𝒆𝒍𝒂𝒔𝒕𝒊𝒄𝒊𝒕𝒚 𝒔𝒐𝒍𝒖𝒕𝒊𝒐𝒏
𝒗𝒂𝒍𝒖𝒆 𝒃𝒚 𝒆𝒙𝒂𝒄𝒕𝒃𝒆𝒍𝒂𝒔𝒕𝒊𝒄𝒊𝒕𝒚 𝒔𝒐𝒍𝒖𝒕𝒊𝒐𝒏
× 𝟏𝟎𝟎%

Theory ῶ %Error σx %Error Τzx %Error
Model 1 2.357 -3.913 3.210 0.312 1.156 -22.93
Model 2 2.515 2.527 3.261 1.906 1.333 .11.13
Model 3 2.532 3.220 3.261 1.906 1.415 -5.667
Model 4 2.529 3.098 3.278 2.437 1.451 -3.267
Model 5 2.513 2.445 3.206 0.187 1.442 3.866
Model 6 2.510 2.323 3.322 3.817 1.430 -4.667
Model 7 2.523 2.853 3.253 1.656 1.397 -6.866
Timoshenko [FSDT] 2.538 3.456 3.000 -6.250 0.984 -34.40
Bernoulli-Euler [EBT] 1.563 -3.628 3.000 -6.250
Timoshenko and Goodier
[Exact]
2.453 0.000 3.200 0.000 0.000 0.00
Here, S=2

Model 1 1.762 -1.288 12.212 0.098 2.389 -20.36
Model 2 1.805 1.120 12.262 0.508 2.836 -5.466
Model 3 1.806 1.176 12.263 0.516 2.908 -3.066
Model 4 1.805 1.120 12.280 0.655 2.993 -0.233
Model 5 1.802 0.952 12.207 0.057 2.982 -0.600
Model 6 1.801 0.896 12.324 1.016 2.957 -1.433
Model 7 1.804 1.064 12.254 0.442 2.882 -3.933
Timoshenko [FSDT] 1.806 1.176 12.00 -1.639 1.969 -34.36
Timoshenko and
Goodier [Exact]
1.785 0.00 12.000 0.000 3.000 0.000
Here, S=4

Model 1 1.595 -0.187 75.216 0.021 6.066 -19.12
Model 2 1.602 0.250 75.266 0.087 7.328 -2.293
Model 3 1.602 0.250 75.268 0.090 7.361 -1.853
Model 4 1.601 0.187 75.284 0.111 7.591 1.213
Model 5 1.601 0.187 75.211 0.014 7.576 1.013
Model 6 1.601 0.187 75.330 0.172 7.513 0.173
Model 7 1.601 0.187 75.259 0.078 7.312 -2.506
Timoshenko [FSDT] 1.602 0.250 75.000 -0.265 4.922 -34.37
Timoshenko and
Goodier [Exact]
1.598 0.000 75.200 0.000 7.500 0.000
Here, S=10

REFERENCE
 Finite Element Method By J.N.Reddy
 Mechanics of laminated composites plates by J.N.Reddy
 Castrenze Polizzotto “From the EulereBernoulli beam to the Timoshenko
one through a sequence of Reddy-type shear deformable beam models of
increasing Order” European Journal of Mechanics A/Solids 53 (2015)
62e74
 A.S. Sayyad “Comparison of various refined beam theories for the bending
and free vibration analysis of thick beams” department of Civil Engineering,
SRES’s College of Engineering, Kopargaon-423601, M.S., India. Received 22
September 2011; received in revised form 19 December 2011
 Anssi T. Karttunena,, Raimo von Hertzena ”Variational formulation of the
static Levinson beam theory” Department of Applied Mechanics, Aalto
University, Finland.
 Zhendong Sun · Lianzhi Yang · Yang Gao “The displacement boundary
conditions for Reddy higher-order shear cantilever beam theory”

Nonlinear Beam theory

More Related Content

What's hot (20)

Similar to Nonlinear Beam theory (20)

Recently uploaded (20)

Nonlinear Beam theory