Particle Classroom Series I: Introduction to Particle Analysis

© 2018 HORIBA, Ltd. All rights reserved.
Introduction to Particle Size Analysis
Jeff Bodycomb, Ph.D.
jeff.bodycomb@horiba.com
www.horiba.com/us/particle

Why Particle Size?
Industry Industry
Ceramic Construction
Oil/rubber Chemical
Battery Pharmaceutical
Electricity Food/Drink
Automobile Paper/Pulp
Mining Ink/Toner
Size affects material behavior and processing across a
number of industries.

Application: Pigment Hiding Power
Operator dependent, need to
wait for drying.
Operator independent, no need
to wait for drying.

Size Terminology
The most common designation is micrometers or
microns. When very small, in colloid region,
measured in nanometers, with electron
microscopes or by dynamic light scattering.
10-10 10-810-9 10-610-7 10-410-5 10-210-3 10-1 10-0
meternanometer
Angstrom
(Å)
micrometer millimeter
micron or µm mnm mm
0.1µm 1.0µm 10µm 100µm
100 nm
Fun tip: Describing your work in terms of beard-seconds
make it much more interesting at parties.
“beard-second”
C-H bond
length

Poll!
Which size ranges do you measure?

Size: Particle Diameter (m)
0.01 0.1 1 10 100 1000
Colloidal
Suspensions and Slurries
DLS – SZ-100
Electron Microscope
Powders
Fine Coarse
Optical Microscopy PSA300, Camsizer
Laser Diffraction – LA-960
Acoustic Spectroscopy
Electrozone Sensing
Disc-Centrifuge
Light Obscuration
0.001
Macromolecules
Nano-Metric
MethodsAppsSizes
Sedimentation
Sieves

The Basics
Which is the most meaningful size?
different
size definitions
different
results

Same data, different size definitions
give different results!
different
size definitions
different
results
xcmin  xArea  xFemax
x [mm ]0 .2 0 .4 0 .6 1
0
10
20
30
40
50
60
70
80
Q3 [% ]
Samp leA_Bas ic_0 .2% _xc_m in_001 .rd f
Samp leA_Bas ic_0 .2% _x_area_001 .rd f
Samp leA_Bas ic_0 .2% _xFemax_001 .rd f
G raph o fmeasu remen t resu lts :
M :...rD is tribu toren-Mee ting CAMDAT Samp leA Samp leA_Bas ic_0 .2% _xc_m in_001 .rd f
Task file :Samp leA_Bas ic_0 .2% .a fg
x [mm ]0 .2 0 .4 0 .6 1
0
10
20
30
40
50
60
70
80
Q3 [% ]
Samp leA_Bas ic_0 .2% _xc_m in_001 .rd f
Samp leA_Bas ic_0 .2% _x_area_001 .rd f
Samp leA_Bas ic_0 .2% _xFemax_001 .rd f
G raph o fmeasu remen t resu lts :
M :...rD is tribu toren-Mee ting CAMDAT Samp leA Samp leA_Bas ic_0 .2% _xc_m in_001 .rd f
Task file :Samp leA_Bas ic_0 .2% .a fg
2 x[mm]

The Basics
What sizes can be measured?

Size Definitions
• Martins’s Diameter: The distance between opposite
sides of a particle measured on a line bisecting the
projected area. To ensure statistical significance all
measurements are made in the same direction
regardless of particle orientation.
• Feret’s Diameter: The distance between parallel
tangents on opposite sides of the particle profile.
Again to insure statistical significance, all
measurements are made in the same direction
regardless of particle orientation.
• Note: Both Martin’s and Feret’s diameters are
generally used for particle size analysis by optical and
electron microscopy.
• Equivalent Circle Diameter: The diameter of a circle
having an area equal to the projected area of the
particle in random orientation. This diameter is usually
determined subjectively and measured by oracular
micrometers called graticules.
• Equivalent Spherical Diameter: The diameter of a
sphere that has the same volume as the irregular
particle being examined.
Martin’s
Diameter
Feret’s Diameter
Equivalent Spherical
Diameter

Particle Orientation
• Martin’s and
Feret’s Diameter’s
will vary as
particles are
viewed in different
orientations. The
result will be a
DISTRIBUTION
from smallest to
largest.
Martin’s
Diameter
Feret’s Diameter
Diameter
Martin’s
Diameter
Feret’s Diameter
Diameter

The Basics
Particle Particle Distribution

The Basics
Particle Size Particle Size Distribution
4 µm

Poll!
What size(s) are reported by your PSA?

Monodisperse vs. Polydisperse
• Monodisperse Distribution:
– All particles are the same size
– Latex standards
• Wide Distribution:
– Particles of Many Sizes
– Everything else
VOLUME
VOLUME
Particle Size Particle Size
Monodisperse Polydisperse

Logarithmic vs. Linear Scale
• Logarithmic X-Axis
Distribution
• Linear X-Axis
Distribution
VOLUME
Particle Size
0 10 20 30 40 50 60 70 80 90 100
VOLUME
Particle Size
0 10 100

Distribution Display
– Represented by series of segments or channels known as
histogram.
– Number of channels based on design, practicality and
aesthetics
VOLUME
Particle Size
Cumulative Distribution
Differential
Distribution
Histogram

Frequency Frequency + cumulative (undersize)
Histogram Multiple frequency + cumulative (undersize)
Your Analyzer’s Displays

Central Values
Mean
Median
and
Mode
Size
Mean
Weighted Average
Center of Gravity
Median
50% Point
Mode
Peak of the distribution
Most common value

Three spheres of diameters 1,2,3 units
What is the average size of these spheres?
Average size = (1+2+3) ÷ 3 =2.00
This is called the D[1,0] - the number mean
1
2
3
What does “Mean” mean?

None of the answers
are wrong they have just
been calculated using
different techniques
X Dnl  
 
[ , ] .1 0
1 2 3
3
2 00
X Dns  
 
[ , ] .2 0
1 4 9
3
216
X Dnv  
 
[ , ] .3 0
1 8 27
3
2 293
X Dsv  
 
 
[ , ] .3 2
1 8 27
1 2 3
2 57
X Dvm  
 
 
[ , ] .4 3
1 16 81
1 8 27
2 72
Many possible Mean values
Number weighted mean Diameter (length)
Volume weighted mean diameter
Volume/surface mean,
Mean volume diameter
Mean surface diameter

Moment Ratios: ISO 9276-2
 qp
q
ii
p
ii
Dn
Dn
qpD












1
],[
qp 











q
ii
i
p
ii
Dn
DDn
qpD
ln
exp],[ qp 
For your reference

D[4,3] which is often referred to as the Volume Mean Diameter [ VMD ]
D [4,3] =


i i
i i
D n
D n
4
3
Monitoring the D[4,3] value in your specification
will emphasize the detection of large particles
Volume-based Mean diameter

Mode
Median
Mean
D[4,3]
Size
Remember: D[4,3] is sensitive to large particles
Central Values revisited
Mean
Weighted Average
Center of Gravity
Median
50% Point
Mode
Peak of the distribution
Most common value

D(v,0.9)D(v,0.1)
Size µm
D(4,3) sensitive to large particles
D(3,2)
D(v,0.5)
median
D(v,1.0)
Never use
the D100!
sensitive to small particles
10% of the particles lie
below this diameter
90% of the particles lie
below this diameter
half are larger than this diameterhalf are smaller than this diameter
Most Common Statistics

Standard Deviation
• Normal (Gaussian)
Distribution Curve
•  = distribution mean
•  = standard deviation
• Exp = base of natural
logarithms
Mean
+1 STD DEV-1 STD DEV
+2 STD DEV-2 STD DEV
68.27%
95.45%
 





 
 2
2
2
exp
2
1



x
Y

Distribution Width
• Polydispersity Index
(PI, PDI)
• Span
• Geometric Std. Dev.
• Variance
• Etc…

Note: Span typically = (d90 – d10)/ d50
For Your Reference

For Your Reference

Error Calculations in LA-960 only
For Your Reference

Skewness

From highest to lowest peak:
red, kurtosis 3
orange, kurtosis 2
green, kurtosis 1.2
black, kurtosis 0,
cyan, kurtosis −0.593762…
blue, kurtosis −1
magenta, kurtosis −1.2
Kurtosis (Peakedness)

r = 1 µm r =2 µm r = 3 µm
v = 4 = 32 = 108
V = 4  r3
3
V*3 = 12 96 324 Total = 12+96+324 = 432
12/432=2.8% 96/432=22.2% 324/432=75%
Number vs. Volume Distributions

Beans!

Equivalent Volume Distributions

Equivalent Number Distributions

Comparing Distribution Bases
• Same material shown as volume, number and area
distribution
Volume
Area
Number
12
4
8
10
6
2
0
PercentinChannel
0.34
4.47
8.82
34.25
0.58
1.15
2.27
17.38Particle Size
Volume Distribution
Mean = 12.65µm
Median=11.58 µm
SA=13467 cm2/cm3
Std Dev.=8.29
Number Distribution
Mean = 0.38µm
Median=0.30 µm
SA=13467 cm2/cm3
Std Dev.=0.40

Statistical Issues with Distributions
• L Neumann, E T White, T Howes (Univ.
Queensland) “What does a mean size
mean?” 2003 AIChE presentation at Session
39 Characterization of Engineered particles
November 16 - 21 San Francisco
Other references:
• L Neumann, T Howes, E T White (2003) Breakage can cause mean
size to increase Dev. Chem. Eng. Mineral Proc. J.
• White E T, Lawrence J. (1970), Variation of volume surface mean for
growing particles, Powder Technology,4, 104 - 107

Does the Mean Match the Process?
• Particle size measurements often made to
monitor a process
– Size reduction (milling)
– Size growth (agglomeration)
• Does the measured/calculated mean diameter
describe the change due to the process?
• It depends on which mean used…

10 x1 m
100 m
breaks into two smaller particles
10 x 1 m
79.4 m
79.4 m
Size Reduction Scenario

Size Reduction: Number Mean
Ten particles of size 1; one of size 100 units
Number mean = D[1, 0] = (10*1 + 1*100)/11 = 10 units
..
Mean = (10*1+2*79.37)/12 = 14.06 units
Surprise, surprise a 40.6% increase!
Largest particle (100) breaks into two of 79.37
(conserves volume/mass: 2 @ 79.373 = 1 @ 1003)
Have broken one
What happens to the number mean?

Size Reduction: Volume Mean
Ten particles of size 1; one of size 100 units
Volume Moment Mean
D[4, 3] = (10*14 + 1*1004)/(10*13 + 1*1003) ~ 100 units
..
New D[4, 3] = (10*14+2*79.374)/(10*13 +2*79.373) ~ 79.37 units
This shows the expected behavior
Largest particle (100) breaks into two of 79.37
Have broken one
What happens to the D[4, 3]?

Number mean = 10 Number mean = 14
Volume mean = 100 Volume mean = 79
Can You See the Problem?

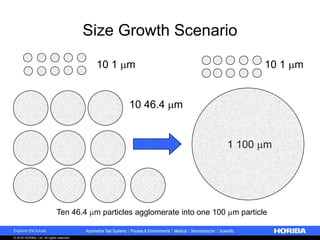
10 1 m 10 1 m
10 46.4 m
1 100 m
Ten 46.4 m particles agglomerate into one 100 m particle
Size Growth Scenario

Growth: Number Mean
Ten particles of size 1; ten of size 46.42
D[1, 0] = (10*1 + 10*46.42)/20 = 23.71 units
.
Mean = (10*1+1*100)/11 = 10 units
Over a 50% decrease!
Ten of 46.42 agglomerate into one of 100
Have agglomerated half; does mean increase?

Growth: Volume Mean
Ten particles of size 1; ten of size 46.42
D[4, 3] = (10*14 + 10*46.424)/(10*13 + 10*46.423)
~ 46.4 units
(Note again the volume moment mean is dominated by the large
particles)
.
D[4, 3] = (10*14+1*1004)/10*13 + 1*1003 ~ 100 units
This shows the expected behavior
Ten of 46.42 agglomerate into one of 100
Have agglomerated half; does mean increase?

Number mean = 24 Number mean = 10
Volume mean = 46 Volume mean = 100
Can You See the Problem?

Practical Implications
• Not just a “party trick” topic!
“Do you know you can break particles and
the mean will increase?”
 Serious. “Did an experiment. I thought I
broke particles but the mean has increased”
(REAL experience)
 Should be aware it can happen!
 Analyse whole size distribution, not mean
alone.

METHODS OF ANALYSIS
PARTICLE MEASUREMENT
METHODS

• Why should one consider various
methods of particle size analysis?
– Material suppliers and users employ many
different types of instruments
– Use a different technique = get a different
answer
– It is important to understand how analysis
methods differ in order to know how to
compare data
PSA Method is Important

Size Range by Technique (m)
0.01 0.1 1 10 100 1000
Colloidal
Suspensions and Slurries
DLS – SZ-100
Electron Microscope
Powders
Fine Coarse
Optical Microscopy PSA300, Camsizer
Laser Diffraction – LA-960
Electrozone Sensing
Disc-Centrifuge
Light Obscuration
0.001
Macromolecules
Nano-Metric
MethodsAppsSizes
Sedimentation
Sieves

Which Analyzer?
Size, desired resolution, and budget determine technology and
product. For a given problem the choice is often clear.
ViewSizer 3000
PSA-300
CAMSIZER X2
CAMSIZER
LA-350
LA-960
SZ-100
Size AND shape

What Size is Measured?
Laser Diffraction
Equivalent Spherical Diameter
Dynamic Light Scattering
Hydrodynamic Radius
Image Analysis
Lengths, Widths, Equivalent Spherical
Equivalent Spherical Diameter

Particle Shape Definitions
Acicular: Needle-shaped, rigid
Angular: Edgy, hard angles
Fibrous: Thread-like, non-rigid
Granular/Blocky: Irregular-shaped, low aspect-ratio
Spherical: Regular-shaped, unity aspect ratio
Aspect ratio: Breadth / length OR Length / breadth
Sphericity: How spherical is the particle?
Roundness: How round is the particle?

Poll!
What are the shapes of your particles?

Hegman Gauge
• Used in paint and coatings industry
– Device has tapered center
channel
– Slurry is placed in
channel, then straight
edge is drawn across it
– “Hegman Number” is
where particles disturb
smooth surface of slurry
– Information from largest
particles only – no
distribution

Sieves
• Weigh % sample caught
on known screen sizes
• Solid particles 30 m – 30
mm (and larger)
Advantages:
Low equipment
cost
Direct
measurement
method
No practical upper
limit
Disadvantages:
Limited lower
range
Time
Consuming
High Labor Cost
Need Large
Sample
Available through www.retsch.com

Electrical Sensing Zone
• Coulter Principle
– Based on change in
conductivity of aperture
as particle traverses.
– Requires conducting
liquid.
– Directly measures
particle volume and
counts.
– High resolution
– Used for blood cell
counting more than
industrial applications

Light Obscuration
• Light Obscuration:
Advantages:
• Particle count available
• USP<788> testing
• High resolution histogram
Disadvantages:
• Dilution required for
particle size analysis
• Prone to cell clogging
Light Source
Liquid Flow
Sensing Zone
DetectorLight is blocked by single particles as
they traverse the light beam

Sedimentation
• Stokes Law
Time
Sedimentation of same density
material in a viscous medium
Vp = Settling velocity of discrete particle
g = Gravity constant
ρp = Density of Particle
ρl = Density of Carrier Fluid
µ = Viscosity of Carrier Fluid
Note: assumes settling of spherical particle
Under-sizes compared to other techniques if non-spherical
 g
V
D
lp
p




18

Sedimentation Issues
• Comparison of Brownian Motion and Gravitational
Settling
• Below 1 micrometer, Brownian motion becomes an appreciable factor in
particle dynamics. Gravity sedimentation may not be an appropriate
measurement technique for very small particles.
Particle Diameter
(In micrometers)
Movement due to
Brownian Motion
Movement due to
Gravitational Settling
0.01 2.36 >> 0.005
0.25 1.49 > 0.0346
0.50 1.052 > 0.1384
1.0 0.745 ~ 0.554
2.5 0.334 < 13.84
10.0 0.236 << 55.4
(Movement in 1 second; Particle density of 2.0 grams/cc)

Particles in suspension undergo Brownian
motion due to bombardment by solvent
molecules in random thermal motion.
Most common technique for sub-micron sizing
Range: 1 nm – 1 m*
* Density dependent, when does settling become prominent motion?
D6
kT
RH


Autocorrelation
Function
Signal
Stokes-Einstein
Dynamic Light Scattering

Manual Microscopy
• Count particles in a given
field of view
• Use graticule to obtain size
• Repeat this process for a
number of fields
• At least hundreds of particles
must be sized
Advantages:
Simple
Inexpensive
Can see shape
Disadvantages:
Slow
Measures very few particles
Very tedious

Dynamic:
Particles flow past camera(s)
Static:
Particles fixed on slide,
stage moves slide
Automated Microscopy

Image Acquisition
and enhancement
Thresholding
Image Processing
Measurements
Objective &
camera
Subjective or
automatic
Decisions or
black box
Advantages:
Quick size + shape info
Statistically valid
High resolution
Particle images
Disadvantages:
Expense
Knowing which
numbers are
important
Automated Microscopy

• Acoustic signal sent into
concentrated sample
• Detector measure
attenuation f (frequency,
distance from source)
Advantages:
• Can accommodate high
sample concentrations
(no dilution)
• Rheological properties
• Also measure zeta potential
Disadvantages:
• Need at least 1 wt% particles
• Need to know wt%
• Minimum sample = 15 ml
Detector
Signal
source
Signal output

Laser Diffraction
•Converts scattered light to
particle size distribution
•Quick, repeatable
•Powders, suspensions
•Most common technique

Key Points
• Particle Analysis is about distributions
• Define terms (results) exactly
– Volume vs. Number
• Different techniques give different answers
since they measure different things
– All are correct…
• Discuss results in terms of technique.

Danke
Большое спасибо
Grazie
Σας ευχαριστούμε
감사합니다
Obrigado
谢谢
ขอบคุณครับ
ありがとうございました
धन्यवाद
நன்ற
Cảm ơn
Dziękuję
Tack ska ni ha
Thank you
Merci
Gracias

Particle Classroom Series I: Introduction to Particle Analysis

More Related Content

What's hot (7)

Similar to Particle Classroom Series I: Introduction to Particle Analysis (20)

More from HORIBA Particle (20)

Recently uploaded (20)

Particle Classroom Series I: Introduction to Particle Analysis