Probabilistic Verification in Computational Systems Design
0 likes572 views
Документ обсуждает вероятностную верификацию в проектировании вычислительных систем, акцентируя внимание на устойчивости к случайным сбоям. Рассматриваются методы защиты, такие как репликация и model checking, которые помогают верифицировать свойства fault-tolerance. Также рассматривается использование марковских цепей для оценки вероятностей и диагностики ошибок.
![Формальный метод вероятностной верификации :Probabilistic Model Checking
Язык описания свойств в Probabilistic Model Checking PC позволяет описывать системы, представленных как Марковская Цепь Дискретного Времени ( DTMC) : (S, s0,P,L), где
−S – конечное множество состояний (“state space”)
−s0 ∈ S – начальное состояние,
−P: S ×S →[0,1] матрица переходов,
Σs’∈SP(s,s’) = 1 для всехs ∈S
L : S →2AP is function labelling states with atomic propositions
AP={try,fail,succ},
L(s0)=, L(s1)={try L(s2)={fail}, L{s3}={succ}
6](https://image.slidesharecdn.com/probabilisticverificationincomputationalsystemsdesign-141124123434-conversion-gate02/85/Probabilistic-Verification-in-Computational-Systems-Design-6-320.jpg)
![Расширение формул CTL на PCTL
−reachability: вероятность достигнуть состояние, удовлетворяюще φ
P~p[ F φ]
−invariance: вероятность выполнения φ всегда истинна
P~p [ G φ]
- Вероятность истинности формулы до момента T
P~p (U≤Tφ)
7](https://image.slidesharecdn.com/probabilisticverificationincomputationalsystemsdesign-141124123434-conversion-gate02/85/Probabilistic-Verification-in-Computational-Systems-Design-7-320.jpg)
Probabilistic Verification in Computational Systems Design
- 1. Вероятностная верификация при проектировании вычислительных систем С.Л. Френкель1 , В.Н.Захаров1, В.Г. Ушаков2 1 Институт проблем информатики (fsergei@mail.ru, VZakharov@ipiran.ru) 2Московский гос. университет им. М.В. Ломоносова, Институт проблем информатики РАН ( Ushakov@akado.ru ).
- 2. Проблема обеспечение устойчивости программно-аппаратных средств к случайным кратковременным сбоям при проектировании. 1. Защита (“укрепление”, hardening) уязвимых элементов (ячеек памяти, регистров) от искажающих воздействий, как внешних (частицы, излучения), так и возможного неспецифицированного поведения. для HW и SW используется репликация: TMR (Triple Modular Redundancy) на аппаратом уровне, или N-version programming (NVP) , состоящее в выполнении N независимых функционально- эквивалентных программ, полученных из одной спецификации. 2
- 3. Model Checking для выбора защищаемых элементов/переменных Model Checking- это — проверка, удовлетворяет ли заданная модель системы формальным спецификациям, описанных средствами LTL, CTL, и.тд.. Мотивация: верификация свойств Fault-tolerance без симуляции. Условие применения- возможность построить конечно- автоматную модель системы. Тогда широкий класс ошибок в любой момент времени можно представить как изменение значения в соответствующем разряде вектора состояний автомата. Например, если в исправной системе должна выполняться формула AG , то можно также рассмотреть условия AG(¬fault ))- т.е. система будет работать правильно, пока не появилась ошибка, и условие, что введение неисправности в модель не приведет к некорректному поведению AG(¬injected ). 3
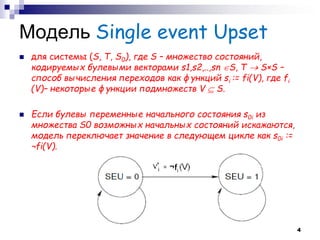
- 4. Модель Single event Upset для системы (S, T, S0), где S – множество состояний, кодируемых булевыми векторами s1,s2,..,sn S, T S×S – способ вычисления переходов как функций si := fi(V), где fi (V)– некоторые функции подмножеств V S. Если булевы переменные начального состояния s0i из множества S0 возможных начальных состояний искажаются, модель переключает значение в следующем цикле как s0i := ¬fi(V). 4
- 5. Поиск угрожаемых элементов (Например,. S. A. Seshia, W.Li, S. Mitra,“Verification-guided soft error resilience”, DATE07, 2007) (i)Каждой переменной модели соответствует множество assertions (формальных LTL/CTL утверждений ) которые задают условия корректного поведения. (ii)изменение одного бита (согласно модели SEU) ведет, к произвольному изменению состояний автомата, ведущему к невыполнению тех или иных assertions. (iii) строится n автоматов (FSM) с измененными битами соответствующего вектора состояния , n-число бит вектора состояний, n+1 раз выполняется Model Checking : один раз для свободной от SEU модели, чтобы проверить, что разработанный проект удовлетворяет требуемому свойству, и n раз для моделей с неисправностями. Элемент системы нуждается в защите, если хотя бы одна из n моделей с неисправностями не удовлетворяет требуемому свойству
- 6. Формальный метод вероятностной верификации :Probabilistic Model Checking Язык описания свойств в Probabilistic Model Checking PC позволяет описывать системы, представленных как Марковская Цепь Дискретного Времени ( DTMC) : (S, s0,P,L), где −S – конечное множество состояний (“state space”) −s0 ∈ S – начальное состояние, −P: S ×S →[0,1] матрица переходов, Σs’∈SP(s,s’) = 1 для всехs ∈S L : S →2AP is function labelling states with atomic propositions AP={try,fail,succ}, L(s0)=, L(s1)={try L(s2)={fail}, L{s3}={succ} 6
- 7. Расширение формул CTL на PCTL −reachability: вероятность достигнуть состояние, удовлетворяюще φ P~p[ F φ] −invariance: вероятность выполнения φ всегда истинна P~p [ G φ] - Вероятность истинности формулы до момента T P~p (U≤Tφ) 7
- 8. Вычислительная сложность PMC для проверки сушественности неисправности СPMC= O(poly(N))·T·|φ|, N- число состояний DTMC, |φ1| - размер формулы, специфицирующей проверяемые свойства, Как правило, poly(N) N6 !!! Полином в приведенной оценке обычно третьей степени, что соответствует сложности известных методов вычисления вероятностей для цепи Маркова. 8
- 9. Проблема нахождение контр-примеров для диагностики результатов В PMC контрпримеры формируются по множеству путей, для которых вероятности не удовлетворяют заданному порогу. Вероятность попадания в момент T в некоторое подмножество состояний S цепи Маркова, такое, что s|=ϕ с матрицей переходных вероятностей P(s, s’) вычисляется как Prob(True U≤ T ϕ) = s|=ϕ P(s,T), P(s,T) – вероятность попадания цепи в состояние s в момент времени T, которая вычисляется для данной DTMC по всем путям перехода в s за T переходов 9
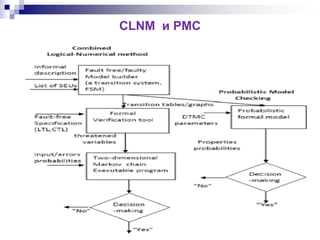
- 10. Комбинированный логико-числовой метод (CLNM) Основная идея вероятностной верификации свойств устойчивости автоматной модели к случайным сбоям состоит в том, что угрожаемые элементы проектируемой системы определяются методом Model Checking, а затем вычисляется вероятность того, что проявление ошибки (SEU) в данном элементе не приведет к проявлению ошибки в результате. 10
- 11. CLNM и PMC 11
- 12. Модель самовосстановления Fault-Free: начальное состояние s0i Faulty: начальное состояние s0j Цепь Mаркова с двумя поглощающими состояниями: A0 : Y=YF до момента перехода траектории переходов автомата в правильное состояние, A1 : Y≠YF
- 13. Модель сбоя 13 Сбой: пара (i,j) at, as- текущее и следующие состояния, X-входы, Y- выходы.
- 14. Вычисление вероятности самовосстановления 14 Вектор начального распределения определяется начальными состояниями исправного и неисправного автоматов. Если исправный автомат в начальный момент 0 находится в состоянии i0, а неисправный – в состоянии j0 ≠ i0, то p(i0,j0)(0) = 1, а остальные координаты вектора нулевые. Матрица переходных вероятностей *вычисляется по известным вероятностям входных переменных автомата. Вероятность самовосстановления за t тактов после прекращения действия помехи:
- 15. Вычислительная сложность CLMN СCLNM =O(poly(size(D))) CCLNM/CPMCT|1| 15
- 16. Задача оценки вероятностей в модели CLNM Задача: оценить вероятности P(xi =1) входных переменных автоматной модели проектирования. Средства:симуляторы и наборы бенчмарков, используемых при отработке устройств. 16
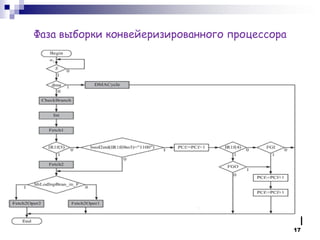
- 17. Фаза выборки конвейеризированного процессора 17
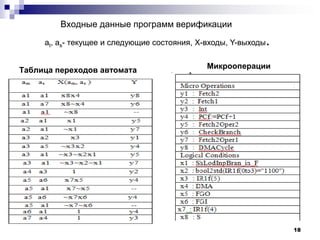
- 18. Входные данные программ верификации Таблица переходов автомата Микрооперации 18 at, as- текущее и следующие состояния, X-входы, Y-выходы.
- 19. Вероятности восстановления Вероятности восстановления через t тактов после сбоя (1,2): (DMAcycle до команды “S” (Start)) SH = (0.0, 0.034, 0.46, 0.55, 0.64, 0.68), и после сбоя (5.2)- (ошибка заполнения программного счетчика): S = (0.00, 0.79, 0.79, 0,85, 0.89, 0.92, 0.93 19
- 20. 20 Thank You!