Properties of estimators (blue)
Download as PPTX, PDF22 likes34,567 views
An estimator in statistics is a rule used to calculate an estimate of a quantity based on observed data, with point estimators providing a single value and interval estimators offering a range. For an estimator to be considered Best Linear Unbiased Estimator (BLUE), it must be linear, unbiased, and efficient with the least variance. Key properties include linearity, unbiasedness, and minimum variance, ensuring the estimator's mean aligns with the true population mean.
Properties of estimators (blue)
- 2. WHAT IS AN ESTIMATOR? • In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data • Example- i. X follows a normal distribution, but we do not know the parameters of our distribution, namely mean (μ) and variance (σ2 ) ii. To estimate the unknowns, the usual procedure is to draw a random sample of size ‘n’ and use the sample data to estimate parameters.
- 3. TWO TYPES OF ESTIMATORS • Point Estimators A point estimate of a population parameter is a single value of a statistic. For example, the sample mean x is a point estimate of the population mean μ. Similarly, the sample proportion p is a point estimate of the population proportion P. • Interval Estimators An interval estimate is defined by two numbers, between which a population parameter is said to lie. For example, a < x < b is an interval estimate of the population mean μ. It indicates that the population mean is greater than a but less than b.
- 4. PROPERTIES OF BLUE • B-BEST • L-LINEAR • U-UNBIASED • E-ESTIMATOR An estimator is BLUE if the following hold: 1. It is linear (Regression model) 2. It is unbiased 3. It is an efficient estimator(unbiased estimator with least variance)
- 5. LINEARITY • An estimator is said to be a linear estimator of (β) if it is a linear function of the sample observations • Sample mean is a linear estimator because it is a linear function of the X values.
- 6. UNBIASEDNESS • A desirable property of a distribution of estimates iS that its mean equals the true mean of the variables being estimated • Formally, an estimator is an unbiased estimator if its sampling distribution has as its expected value equal to the true value of population. • We also write this as follows: Similarly, if this is not the case, we say that the estimator is biased
- 7. • Similarly, if this is not the case, we say that the estimator is biased • Bias=E( ) - β
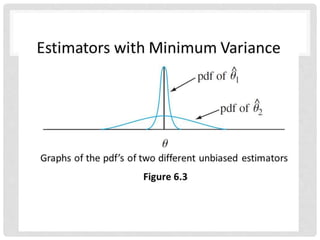
- 9. MINIMUM VARIANCE • Just as we wanted the mean of the sampling distribution to be centered around the true population , so too it is desirable for the sampling distribution to be as narrow (or precise) as possible. – Centering around “the truth” but with high variability might be of very little use • One way of narrowing the sampling distribution is to increase the sampling size
- 11. BLUE
Editor's Notes
- #3: Suppose there is a fixed parameter that needs to be estimated. Then an "estimator" is a function that maps the sample space to a set of sample estimates. An estimator of is usually denoted by the symbol .