Robust Repositioning in Large-scale Networks
0 likes539 views
This document discusses robust optimization models for empty trailer repositioning in large-scale freight consolidation networks. It presents a two-stage robust optimization model that minimizes costs of planned trailer movements while ensuring the existence of feasible recovery movements for uncertain future demand scenarios. The model considers recovery flows and bounds the vulnerability of subsets of nodes to address future feasibility. Challenges include controlling model conservatism and appropriately applying the two-stage model in large, dynamic networks with rolling horizons.
![Two-‐stage
robust
reposi.oning
Second stage uncertain demand
t=0 t=1 t=2 t=3 t=4 t=5
A
B
Intervals on future loaded moves [a , a ]
C
[0, 2]
D
E](https://image.slidesharecdn.com/odysseuserera2012-120525010737-phpapp01/85/Robust-Repositioning-in-Large-scale-Networks-11-320.jpg)
![Two-‐stage
robust
reposi.oning
• Worst-‐case
vulnerability
of
inbound-‐closed
set
xa ≥ ν(U ) ∀ U is inbound-closed
a∈δ + (U )∩I
ν(U ) = a − a + bi
a∈δ + (U ) a∈δ − (U ) i∈U
t=0 t=1 t=2 t=3 t=4 t=5
A
[0, 2]
B
[1, 5]
C](https://image.slidesharecdn.com/odysseuserera2012-120525010737-phpapp01/85/Robust-Repositioning-in-Large-scale-Networks-16-320.jpg)
![Controlling
conserva.sm
• Exclude
extreme
scenarios
– Narrow
the
width
of
intervals
[a , a ]
– Limit
to
k
the
number
of
uncertain
quan..es
that
may
simultaneously
take
on
an
extreme
quan.ty
• Challenges
for
large
.me-‐expanded
networks
– Very
large
numbers
of
inbound-‐closed
sets
and
associated
robust
constraints:
O(τ nS )
– Difficult
to
judge
in
advance
which
robust
constraints
will
be
ac.ve](https://image.slidesharecdn.com/odysseuserera2012-120525010737-phpapp01/85/Robust-Repositioning-in-Large-scale-Networks-19-320.jpg)
![Two-‐stage
robust
reposi.oning
• Bounded
vulnerability
of
inbound-‐closed
set
max (a − a )za + (a − a )za | za = k
z
a∈δ + (U ) a∈δ − (U )
t=0 t=1 t=2 t=3 t=4 t=5
A
[0, 2]
B
[1, 5]
C](https://image.slidesharecdn.com/odysseuserera2012-120525010737-phpapp01/85/Robust-Repositioning-in-Large-scale-Networks-20-320.jpg)
Robust Repositioning in Large-scale Networks
- 1. Robust Empty Reposi.oning in Large-‐Scale Freight Consolida.on Networks Alan Erera1, Antonio Carbajal1, Mar.n Savelsbergh2 1 School of Industrial and Systems Engineering, Georgia Tech 2 University of Newcastle, Australia Odysseus 2012
- 2. What to remember 1. Robust models for empty mobile resource management pragma.c and effec.ve 2. Empty resource hubs useful for very large-‐ scale reposi.oning networks 3. Rolling-‐horizon deployments of two-‐stage robust op.miza.on models should u.lize: – short robust horizons – rolling robust constraints
- 3. Consolida.on networks Customer Satellite terminal Hub terminal origin destination
- 4. Consolida.on networks Net weekly surplus -3 Satellite terminal of empty trailers Hub terminal +5 -5 -1 +2 +4 +1 +1 -1 +1 +1 +3 +4 +3 -4 -3 0 +3 +2 +1 -3 0 -6 +1 -2 -1
- 5. Dynamic trailer reposi.oning • Large-‐scale terminal network – 250+ satellites and hubs • Dynamics – Several decision epochs daily – Today’s projected demand for trailers accurate – Tomorrow’s (and beyond) significantly uncertain • Goal – Best empty reposi.oning plan each epoch
- 6. Modeling approaches • Determinis.c rolling-‐horizon network flow LP – Assume that trailer demands tomorrow (and beyond) behave as expected • Stochas.c models – Minimize expected costs given probabilis.c model of demand – Powell (87), Frantzeskakis and Powell (90), Cheung and Powell (96), Godfrey and Powell (02a, 02b) – Crainic (93), Di Francesco, et al. (09)
- 7. Modeling approaches • Robust op.miza.on models – Bertsimas and Sim (03), Atamturk and Zhang (07) – Morales (06), Erera et. al. (09) • Two-‐stage model • Explicit focus on future feasibility • Minimize cost of planned movements such that a feasible set of recovery movements exists for each non-‐ extreme scenario
- 8. Two-‐stage robust reposi.oning First stage decisions t=0 t=1 t=2 t=3 t=4 t=5 A B C D E
- 9. Two-‐stage robust reposi.oning First stage net supply bi t=0 t=1 t=2 t=3 t=4 t=5 A Initial trailers B +2 Known and expected future loaded moves C +6 -2 -1 D E +2 +1
- 10. Two-‐stage robust reposi.oning Second stage “recovery” decisions t=0 t=1 t=2 t=3 t=4 t=5 A B C D E
- 11. Two-‐stage robust reposi.oning Second stage uncertain demand t=0 t=1 t=2 t=3 t=4 t=5 A B Intervals on future loaded moves [a , a ] C [0, 2] D E
- 12. Two-‐stage robust reposi.oning • First stage network flow min c a xa a xa − x a = bi ∀i∈N a∈δ + (i) a∈δ − (i) xa ≥ 0 and integer ∀ a ∈ A • Second stage “recovery flow” for each scenario wa (ω) − wa (ω) = bi (ω) − bi ∀i∈N a∈δ + (i) a∈δ − (i) xa + wa (ω) ≥ 0 ∀a∈A
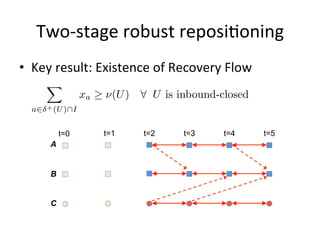
- 13. Two-‐stage robust reposi.oning • Key result: Existence of Recovery Flow xa ≥ ν(U ) ∀ U is inbound-closed a∈δ + (U )∩I t=0 t=1 t=2 t=3 t=4 t=5 A B C
- 14. Two-‐stage robust reposi.oning • Inbound closed set – node set with no incoming recovery transporta.on arcs t=0 t=1 t=2 t=3 t=4 t=5 A B C
- 15. Two-‐stage robust reposi.oning • Inbound closed set – this example not inbound-‐closed t=0 t=1 t=2 t=3 t=4 t=5 A B C
- 16. Two-‐stage robust reposi.oning • Worst-‐case vulnerability of inbound-‐closed set xa ≥ ν(U ) ∀ U is inbound-closed a∈δ + (U )∩I ν(U ) = a − a + bi a∈δ + (U ) a∈δ − (U ) i∈U t=0 t=1 t=2 t=3 t=4 t=5 A [0, 2] B [1, 5] C
- 17. Challenges (1) Smart recovery network – Low-‐cost moves (since costs not modeled) – Opera.onally simple (2) Appropriate use of two-‐stage model – Controlling conserva.sm pragma.cally – Special considera.ons for rolling horizon implementa.on – Solvable (but very large scale) MIPs
- 18. Smart recovery network Empty hubs Region 1 Region 2 Region 3
- 19. Controlling conserva.sm • Exclude extreme scenarios – Narrow the width of intervals [a , a ] – Limit to k the number of uncertain quan..es that may simultaneously take on an extreme quan.ty • Challenges for large .me-‐expanded networks – Very large numbers of inbound-‐closed sets and associated robust constraints: O(τ nS ) – Difficult to judge in advance which robust constraints will be ac.ve
- 20. Two-‐stage robust reposi.oning • Bounded vulnerability of inbound-‐closed set max (a − a )za + (a − a )za | za = k z a∈δ + (U ) a∈δ − (U ) t=0 t=1 t=2 t=3 t=4 t=5 A [0, 2] B [1, 5] C
- 21. Appropriate use of two-‐stage model Terminal limit known future A B C D – inbound-‐closed sets with L+1 terminals or fewer
- 22. Appropriate use of two-‐stage model Robust horizon known future A B C D robust horizon – inbound-‐closed sets include no nodes aher RH
- 23. Appropriate use of two-‐stage model Rolling-horizon robust constraints known future A B C D robust horizon – add constraints now for future horizon rolls • assume that demand intervals do not change
- 24. Appropriate use of two-‐stage model Rolling-horizon robust constraints known future A B C D robust horizon – add constraints now for future horizon rolls • assume that demand intervals do not change
- 25. Tes.ng the ideas • Givens – Historical data from a na.onal consolida.on trucking carrier – Loaded moves involve 264 terminals – Reposi.oning moves (truck and rail) – 10 empty hubs – At most 4 daily dispatch .mes per terminal – Wide forecast intervals on loaded demands (+/-‐ 50% of actual)
- 26. Tes.ng the ideas • Horizons – 14 weeks of data – Planning horizon of 7 days for each model • Network size for 7-‐day planning horizon – 5,000 .me-‐space nodes – 300,000 arcs • Primarily reposi.oning arcs • Limited connec.ons
- 27. Tes.ng the ideas • Simulate – Assume today’s loaded demands known – Solve model, implement today’s decisions • Assume trailer deficits covered by an outsourced trailer – Draw realiza.on of tomorrow’s demands – Repeat
- 28. Figure 18: Unmet demands on a given day - Scenario 2 Results Figure 19: Cumulative unmet demands - Scenario 2
- 29. Figure 20: Execution costs on a given day - Scenario 2 Results Figure 21: Cumulative execution costs - Scenario 2
- 30. Short planning horizons Figure 22: Cumulative unmet demands with different planning horizons - Scenario 1
- 31. Next steps • Refinements – More reasonable model of true uncertainty in demand – Understand sources of cost escala.on, including if and where excessive conserva.sm introduced • Empty hub selec.on • Fleet size versus reposi.oning cost for robust plans
- 32. What to remember 1. Robust models for empty mobile resource management pragma.c and effec.ve 2. Empty resource hubs useful for very large-‐ scale reposi.oning networks 3. Rolling-‐horizon deployments of two-‐stage robust op.miza.on models should u.lize: – short robust horizons – rolling robust constraints