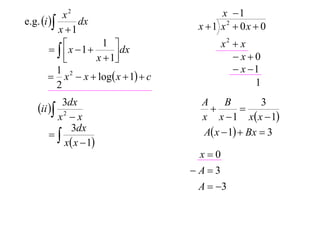SlideShare a Scribd company logo

X2 T05 06 partial fractions (2010)

N
Nigel Simmons

文档讨论了通过部分分式分解进行积分的方法，具体包括当分母的次数大于或等于分子时的除法技巧，以及如何处理线性和多项式因子。它提供了对部分函数的分解示例和相应的积分计算。文档还涉及了特定例子的逐步解决方案。

Education
1 of 48
Downloaded 18 times
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
Integration By Partial Fractions  Ax To find;  dx P x 
Integration By Partial Fractions  Ax To find;  dx P x  1 If degA x   degP x , perform a division
Integration By Partial Fractions  Ax To find;  dx P x  1 If degA x   degP x , perform a division 2 If degA x   degP x , factorise P x 
Integration By Partial Fractions  Ax To find;  dx P x  1 If degA x   degP x , perform a division 2 If degA x   degP x , factorise P x  A a) for linear factor  x  a , write xa
Integration By Partial Fractions  Ax To find;  dx P x  1 If degA x   degP x , perform a division 2 If degA x   degP x , factorise P x  A a) for linear factor  x  a , write xa b) for multiple linear factors  x  a  , write n A B C   x  a x  a 2  x  a n
Integration By Partial Fractions  Ax To find;  dx P x  1 If degA x   degP x , perform a division 2 If degA x   degP x , factorise P x  A a) for linear factor  x  a , write xa b) for multiple linear factors  x  a  , write n A B C   x  a x  a 2  x  a n Ax  B c) for polynomial factors e.g. ax  bx  c, write 2 2 ax  bx  c
x2 e.g. i  dx x 1
x2 x e.g. i  dx x 1 x2  0x  0 x 1 x2  x
x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x x0
x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x x0  x 1
x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x x0  x 1 1
x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x   x 1 1     dx x  1 x0  x 1 1
x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x   x 1 1     dx x  1 x0 1  x 1  x 2  x  log x  1  c 2 1
x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x   x 1 1     dx x  1 x0 1  x 1  x 2  x  log x  1  c 2 1 3dx ii  x2  x
x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x   x 1 1     dx x  1 x0 1  x 1  x 2  x  log x  1  c 2 1 3dx ii  x2  x 3dx  x x  1
x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x   x 1 1     dx x  1 x0 1  x 1  x 2  x  log x  1  c 2 1 3dx A B 3 ii  2   x x x x  1 x x  1 3dx  x x  1
x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x   x 1 1     dx x  1 x0 1  x 1  x 2  x  log x  1  c 2 1 3dx A B 3 ii    x2  x x x  1 x x  1  3dx A x  1  Bx  3 x x  1
x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x   x 1 1     dx x  1 x0 1  x 1  x 2  x  log x  1  c 2 1 3dx A B 3 ii    x2  x x x  1 x x  1  3dx A x  1  Bx  3 x x  1 x0 A3 A  3
x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x   x 1 1     dx x  1 x0 1  x 1  x 2  x  log x  1  c 2 1 3dx A B 3 ii    x2  x x x  1 x x  1  3dx A x  1  Bx  3 x x  1 x0 x 1 A3 B3 A  3
x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x   x 1 1     dx x  1 x0 1  x 1  x 2  x  log x  1  c 2 1 3dx A B 3 ii    x2  x x x  1 x x  1  3dx A x  1  Bx  3 x x  1  3 3  x0 x 1     dx A3 B3  x  x  1 A  3
x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x   x 1 1     dx x  1 x0 1  x 1  x 2  x  log x  1  c 2 1 3dx A B 3 ii    x2  x x x  1 x x  1  3dx A x  1  Bx  3 x x  1  3 3  x0 x 1     dx A3 B3  x  x  1  3 log x  3 log x  1  c A  3
x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x   x 1 1     dx x  1 x0 1  x 1  x 2  x  log x  1  c 2 1 3dx A B 3 ii    x2  x x x  1 x x  1  3dx A x  1  Bx  3 x x  1  3 3  x0 x 1     dx A3 B3  x  x  1  3 log x  3 log x  1  c A  3 x  1  3 log  c  x 
x5 iii  2 dx x  3 x  10
x5 iii  2 dx x  3 x  10 x5  dx  x  5 x  2
x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2
x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2 x  2  7B  3 3 B 7
x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2 x  2 x5  7B  3 7 A  10 3 10 B A 7 7
x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2 x  2 x5  10 3   7B  3 7 A  10     dx  7  x  5  7  x  2  3 10 B A 7 7
x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2 x  2 x5  10 3   7B  3 7 A  10     dx  7  x  5  7  x  2  3 10 10 3 B A  log x  5  log x  2   c 7 7 7 7
x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2 x  2 x5  10 3   7B  3 7 A  10     dx  7  x  5  7  x  2  3 10 10 3 B A  log x  5  log x  2   c 7 7 7 7 dx iv  3 x x
x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2 x  2 x5  10 3   7B  3 7 A  10     dx  7  x  5  7  x  2  3 10 10 3 B A  log x  5  log x  2   c 7 7 7 7 dx iv  3 x x dx  xx 2  1
x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2 x  2 x5  10 3   7B  3 7 A  10     dx  7  x  5  7  x  2  3 10 10 3 B A  log x  5  log x  2   c 7 7 7 7 A Bx  C 1 iv  3 dx  2  x x x x  1 xx 2  1  dx Ax 2  1   Bx  C x  1 xx 2  1
x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2 x  2 x5  10 3   7B  3 7 A  10     dx  7  x  5  7  x  2  3 10 10 3 B A  log x  5  log x  2   c 7 7 7 7 A Bx  C 1 iv  3 dx  2  x x x x  1 xx 2  1  dx Ax 2  1   Bx  C x  1 xx 2  1 x0 A 1
x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2 x  2 x5  10 3   7B  3 7 A  10     dx  7  x  5  7  x  2  3 10 10 3 B A  log x  5  log x  2   c 7 7 7 7 A Bx  C 1 iv  3 dx  2  x x x x  1 xx 2  1  dx Ax 2  1   Bx  C x  1 xx 2  1 xi x0 A 1  B  Ci  1
x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2 x  2 x5  10 3   7B  3 7 A  10     dx  7  x  5  7  x  2  3 10 10 3 B A  log x  5  log x  2   c 7 7 7 7 A Bx  C 1 iv  3 dx  2  x x x x  1 xx 2  1  dx Ax 2  1   Bx  C x  1 xx 2  1 xi x0 A 1  B  Ci  1 B  1 C  0
x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2 x  2 x5  10 3   7B  3 7 A  10     dx  7  x  5  7  x  2  3 10 10 3 B A  log x  5  log x  2   c 7 7 7 7 A Bx  C 1 iv  3 dx  2  x x x x  1 xx 2  1  dx Ax 2  1   Bx  C x  1 xx 2  1 xi x0    1  x  dx  A 1  B  Ci  1  x x  1 2 B  1 C  0
x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2 x  2 x5  10 3   7B  3 7 A  10     dx  7  x  5  7  x  2  3 10 10 3 B A  log x  5  log x  2   c 7 7 7 7 A Bx  C 1 iv  3 dx  2  x x x x  1 xx 2  1  dx Ax 2  1   Bx  C x  1 xx 2  1 xi x0    1  x  dx  A 1  B  Ci  1  x x  1 2 B  1 C  0  log x  logx 2  1  c 1 2
xdx v   x  12 x 2  1
v  xdx A B Cx  D x   2   x  12 x 2  1  x  1  x  12 x  1  x  12 x 2  1 A x  1x 2  1  B x 2  1  Cx  D  x  1  x 2
v  xdx A B Cx  D x   2   x  12 x 2  1  x  1  x  12 x  1  x  12 x 2  1 A x  1x 2  1  B x 2  1  Cx  D  x  1  x 2 x  1 2 B  1 1 B 2
v  xdx A B Cx  D x   2   x  12 x 2  1  x  1  x  12 x  1  x  12 x 2  1 A x  1x 2  1  B x 2  1  Cx  D  x  1  x 2 x  1 xi 2 B  1  2C  2 Di  i 1 B 2
v  xdx A B Cx  D x   2   x  12 x 2  1  x  1  x  12 x  1  x  12 x 2  1 A x  1x 2  1  B x 2  1  Cx  D  x  1  x 2 x  1 xi 2 B  1  2C  2 Di  i 1 1 C 0 D B 2 2
v  xdx A B Cx  D x   2   x  12 x 2  1  x  1  x  12 x  1  x  12 x 2  1 A x  1x 2  1  B x 2  1  Cx  D  x  1  x 2 x  1 xi 2 B  1  2C  2 Di  i 1 1 C 0 D B 2 2 x0 2A  B  D  0 1 1 2A    0 2 2 A0
v  xdx A B Cx  D x   2   x  12 x 2  1  x  1  x  12 x  1  x  12 x 2  1 A x  1x 2  1  B x 2  1  Cx  D  x  1  x 2  1 x  1 xi 1      2 x  1 2x  1 2 2  dx 2 B  1  2C  2 Di  i 1 1 C 0 D B 2 2 x0 2A  B  D  0 1 1 2A    0 2 2 A0
v  xdx A B Cx  D x   2   x  12 x 2  1  x  1  x  12 x  1  x  12 x 2  1 A x  1x 2  1  B x 2  1  Cx  D  x  1  x 2  1 x  1 xi 1      2 x  1 2x  1 2 2  dx 2 B  1  2C  2 Di  i 1 1 C 0 D 1  1  B 2     x  1  2 2 2  x  1 dx 2 x0 2A  B  D  0 1 1 2A    0 2 2 A0
v  xdx A B Cx  D x   2   x  12 x 2  1  x  1  x  12 x  1  x  12 x 2  1 A x  1x 2  1  B x 2  1  Cx  D  x  1  x 2  1 x  1 xi 1      2 x  1 2x  1 2 2  dx 2 B  1  2C  2 Di  i 1 1 C 0 D 1  1  B 2     x  1  2 2 2  x  1 dx 2 x0 1    x  11 1  2A  B  D  0    tan x   c 2  1  1 1 2A    0 2 2 A0
v  xdx A B Cx  D x   2   x  12 x 2  1  x  1  x  12 x  1  x  12 x 2  1 A x  1x 2  1  B x 2  1  Cx  D  x  1  x 2  1 x  1 xi 1      2 x  1 2x  1 2 2  dx 2 B  1  2C  2 Di  i 1 1 C 0 D 1  1  B 2     x  1  2 2 2  x  1 dx 2 x0 1    x  11 1  2A  B  D  0    tan x   c 2  1  1 1 2A    0 1 1  2 2    tan 1 x   c A0 2  x 1 
v  xdx A B Cx  D x   2   x  12 x 2  1  x  1  x  12 x  1  x  12 x 2  1 A x  1x 2  1  B x 2  1  Cx  D  x  1  x 2  1 x  1 xi 1      2 x  1 2x  1 2 2  dx 2 B  1  2C  2 Di  i 1 1 C 0 D 1  1  B 2     x  1  2 2 2  x  1 dx 2 x0 1    x  11 1  2A  B  D  0    tan x   c 2  1  1 1 2A    0 1 1  Exercise 2G; 2 2    tan 1 x   c 1, 3, 5, 7 to 21 A0 2  x 1 

More Related Content

PDF
Tabla 1 derivadas
Rosa Cristina De Pena Olivares
 
PDF
11X1 T14 06 derivative times function
Nigel Simmons
 
PDF
12X1 T06 01 integration using substitution (2010)
Nigel Simmons
 
PDF
中山女高99下高3第1次段考數學科 自然組
lyt199529
 
PDF
X2 T05 07 quadratic denominators (2010)
Nigel Simmons
 
DOC
1 4對數函數
leohonesty0814
 
PPT
2牛顿运动定律
vincent930218
 
ZIP
1 4對數函數
leohonesty0814
 
Tabla 1 derivadas
Rosa Cristina De Pena Olivares
 
11X1 T14 06 derivative times function
Nigel Simmons
 
12X1 T06 01 integration using substitution (2010)
Nigel Simmons
 
中山女高99下高3第1次段考數學科 自然組
lyt199529
 
X2 T05 07 quadratic denominators (2010)
Nigel Simmons
 
1 4對數函數
leohonesty0814
 
2牛顿运动定律
vincent930218
 
1 4對數函數
leohonesty0814
 

Similar to X2 T05 06 partial fractions (2010) (20)

PDF
X2 t04 06 partial fractions (2013)
Nigel Simmons
 
PDF
X2 t04 06 partial fractions (2012)
Nigel Simmons
 
PDF
12X1 T06 01 integration using substitution (2011)
Nigel Simmons
 
PDF
X2 t04 07 quadratic denominators (2013)
Nigel Simmons
 
PDF
X2 t04 07 quadratic denominators (2012)
Nigel Simmons
 
PDF
X2 T04 07 quadratic denominators (2011)
Nigel Simmons
 
PDF
11X1 T17 03 indefinite integral
Nigel Simmons
 
PDF
11X1 T14 03 indefinite integral
Nigel Simmons
 
PDF
11 x1 t16 03 indefinite integral (2012)
Nigel Simmons
 
PDF
11X1 T16 03 indefinite integral (2011)
Nigel Simmons
 
PDF
11X1 T17 06 derivative times function (2010)
Nigel Simmons
 
PDF
11X1 T16 06 derivative times function (2011)
Nigel Simmons
 
PDF
11 x1 t16 06 derivative times function
Nigel Simmons
 
PDF
11. límite de funciones
Lourdes Moreno Márquez
 
PDF
11X1 T09 04 chain rule (2010)
Nigel Simmons
 
PDF
11X1 T09 04 chain rule (2011)
Nigel Simmons
 
PDF
曲線弧長
永鴻 卓
 
PDF
11 x1 t09 04 chain rule (2012)
Nigel Simmons
 
PDF
12X1 T01 02 differentiating logs (2010)
Nigel Simmons
 
PDF
12 x1 t01 02 differentiating logs (2013)
Nigel Simmons
 
X2 t04 06 partial fractions (2013)
Nigel Simmons
 
X2 t04 06 partial fractions (2012)
Nigel Simmons
 
12X1 T06 01 integration using substitution (2011)
Nigel Simmons
 
X2 t04 07 quadratic denominators (2013)
Nigel Simmons
 
X2 t04 07 quadratic denominators (2012)
Nigel Simmons
 
X2 T04 07 quadratic denominators (2011)
Nigel Simmons
 
11X1 T17 03 indefinite integral
Nigel Simmons
 
11X1 T14 03 indefinite integral
Nigel Simmons
 
11 x1 t16 03 indefinite integral (2012)
Nigel Simmons
 
11X1 T16 03 indefinite integral (2011)
Nigel Simmons
 
11X1 T17 06 derivative times function (2010)
Nigel Simmons
 
11X1 T16 06 derivative times function (2011)
Nigel Simmons
 
11 x1 t16 06 derivative times function
Nigel Simmons
 
11. límite de funciones
Lourdes Moreno Márquez
 
11X1 T09 04 chain rule (2010)
Nigel Simmons
 
11X1 T09 04 chain rule (2011)
Nigel Simmons
 
曲線弧長
永鴻 卓
 
11 x1 t09 04 chain rule (2012)
Nigel Simmons
 
12X1 T01 02 differentiating logs (2010)
Nigel Simmons
 
12 x1 t01 02 differentiating logs (2013)
Nigel Simmons
 
Ad

More from Nigel Simmons (20)

PPT
Goodbye slideshare UPDATE
Nigel Simmons
 
PPT
Goodbye slideshare
Nigel Simmons
 
PDF
12 x1 t02 02 integrating exponentials (2014)
Nigel Simmons
 
PDF
11 x1 t01 03 factorising (2014)
Nigel Simmons
 
PDF
11 x1 t01 02 binomial products (2014)
Nigel Simmons
 
PDF
12 x1 t02 01 differentiating exponentials (2014)
Nigel Simmons
 
PDF
11 x1 t01 01 algebra & indices (2014)
Nigel Simmons
 
PDF
12 x1 t01 03 integrating derivative on function (2013)
Nigel Simmons
 
PDF
12 x1 t01 02 differentiating logs (2013)
Nigel Simmons
 
PDF
12 x1 t01 01 log laws (2013)
Nigel Simmons
 
PDF
X2 t02 04 forming polynomials (2013)
Nigel Simmons
 
PDF
X2 t02 03 roots & coefficients (2013)
Nigel Simmons
 
PDF
X2 t02 02 multiple roots (2013)
Nigel Simmons
 
PDF
X2 t02 01 factorising complex expressions (2013)
Nigel Simmons
 
PDF
11 x1 t16 07 approximations (2013)
Nigel Simmons
 
PDF
11 x1 t16 06 derivative times function (2013)
Nigel Simmons
 
PDF
11 x1 t16 05 volumes (2013)
Nigel Simmons
 
PDF
11 x1 t16 04 areas (2013)
Nigel Simmons
 
PDF
11 x1 t16 03 indefinite integral (2013)
Nigel Simmons
 
PDF
11 x1 t16 02 definite integral (2013)
Nigel Simmons
 
Goodbye slideshare UPDATE
Nigel Simmons
 
Goodbye slideshare
Nigel Simmons
 
12 x1 t02 02 integrating exponentials (2014)
Nigel Simmons
 
11 x1 t01 03 factorising (2014)
Nigel Simmons
 
11 x1 t01 02 binomial products (2014)
Nigel Simmons
 
12 x1 t02 01 differentiating exponentials (2014)
Nigel Simmons
 
11 x1 t01 01 algebra & indices (2014)
Nigel Simmons
 
12 x1 t01 03 integrating derivative on function (2013)
Nigel Simmons
 
12 x1 t01 02 differentiating logs (2013)
Nigel Simmons
 
12 x1 t01 01 log laws (2013)
Nigel Simmons
 
X2 t02 04 forming polynomials (2013)
Nigel Simmons
 
X2 t02 03 roots & coefficients (2013)
Nigel Simmons
 
X2 t02 02 multiple roots (2013)
Nigel Simmons
 
X2 t02 01 factorising complex expressions (2013)
Nigel Simmons
 
11 x1 t16 07 approximations (2013)
Nigel Simmons
 
11 x1 t16 06 derivative times function (2013)
Nigel Simmons
 
11 x1 t16 05 volumes (2013)
Nigel Simmons
 
11 x1 t16 04 areas (2013)
Nigel Simmons
 
11 x1 t16 03 indefinite integral (2013)
Nigel Simmons
 
11 x1 t16 02 definite integral (2013)
Nigel Simmons
 
Ad

Recently uploaded (20)

PPTX
3分钟读懂福特汉姆大学毕业证Fordham毕业证学历认证
hebjad
 
PPTX
3分钟读懂贝尔法斯特女王大学毕业证QUB毕业证学历认证
fomlev
 
PPTX
3分钟读懂肯塔基大学毕业证UK毕业证学历认证
kamlaf
 
PPTX
3分钟读懂加州大学欧文分校毕业证UCI毕业证学历认证
tozfoh
 
PPTX
3分钟读懂伦敦南岸大学毕业证LSBU毕业证学历认证
sofwah2
 
PPTX
3分钟读懂利物浦约翰摩尔大学毕业证LJMU毕业证学历认证
sofwah2
 
PPTX
《HSK标准教程4下》第15课课件new.pptx HSK chapter 15 pptx
MujaddidRabbani
 
PPTX
3分钟读懂拉夫堡大学毕业证LU毕业证学历认证
seoruc
 
PPTX
3分钟读懂伦敦商学院毕业证LBS毕业证学历认证
sofwah2
 
PDF
黑客出手，分数我有！安全可靠的技术支持，让你的GPA瞬间提升，留学之路更加顺畅！【微信：viphuzhao】
→viphuzhao 微信
 
PPTX
3分钟读懂圣安德鲁斯大学毕业证StAnd毕业证学历认证
mifnee
 
PPTX
模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板
idiot040713
 
PPTX
3分钟读懂诺里奇艺术大学毕业证NUA毕业证学历认证
seoruc
 
PPTX
3分钟读懂渥太华大学毕业证UO毕业证学历认证
keefel1
 
PPTX
3分钟读懂滑铁卢大学毕业证Waterloo毕业证学历认证
keefel1
 
PPTX
3分钟读懂索尔福德大学毕业证Salford毕业证学历认证
fomlev
 
PPTX
3分钟读懂伦敦大学学院毕业证UCL毕业证学历认证
sofwah2
 
PPTX
3分钟读懂曼彻斯特大学毕业证UoM毕业证学历认证
seoruc
 
PPTX
3分钟读懂皇家艺术学院毕业证RCA毕业证学历认证
fomlev
 
PDF
想要安全提高成绩？我们的黑客技术采用深度伪装和多层加密手段，确保你的信息安全无忧。价格公道，流程简单，同时提供全面的信息保护和事后痕迹清理，让你轻松提升G...
→viphuzhao 微信
 
3分钟读懂福特汉姆大学毕业证Fordham毕业证学历认证
hebjad
 
3分钟读懂贝尔法斯特女王大学毕业证QUB毕业证学历认证
fomlev
 
3分钟读懂肯塔基大学毕业证UK毕业证学历认证
kamlaf
 
3分钟读懂加州大学欧文分校毕业证UCI毕业证学历认证
tozfoh
 
3分钟读懂伦敦南岸大学毕业证LSBU毕业证学历认证
sofwah2
 
3分钟读懂利物浦约翰摩尔大学毕业证LJMU毕业证学历认证
sofwah2
 
《HSK标准教程4下》第15课课件new.pptx HSK chapter 15 pptx
MujaddidRabbani
 
3分钟读懂拉夫堡大学毕业证LU毕业证学历认证
seoruc
 
3分钟读懂伦敦商学院毕业证LBS毕业证学历认证
sofwah2
 
黑客出手，分数我有！安全可靠的技术支持，让你的GPA瞬间提升，留学之路更加顺畅！【微信：viphuzhao】
→viphuzhao 微信
 
3分钟读懂圣安德鲁斯大学毕业证StAnd毕业证学历认证
mifnee
 
模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板模板
idiot040713
 
3分钟读懂诺里奇艺术大学毕业证NUA毕业证学历认证
seoruc
 
3分钟读懂渥太华大学毕业证UO毕业证学历认证
keefel1
 
3分钟读懂滑铁卢大学毕业证Waterloo毕业证学历认证
keefel1
 
3分钟读懂索尔福德大学毕业证Salford毕业证学历认证
fomlev
 
3分钟读懂伦敦大学学院毕业证UCL毕业证学历认证
sofwah2
 
3分钟读懂曼彻斯特大学毕业证UoM毕业证学历认证
seoruc
 
3分钟读懂皇家艺术学院毕业证RCA毕业证学历认证
fomlev
 
想要安全提高成绩？我们的黑客技术采用深度伪装和多层加密手段，确保你的信息安全无忧。价格公道，流程简单，同时提供全面的信息保护和事后痕迹清理，让你轻松提升G...
→viphuzhao 微信
 

X2 T05 06 partial fractions (2010)

  • 1. Integration By Partial Fractions  Ax To find;  dx P x 
  • 2. Integration By Partial Fractions  Ax To find;  dx P x  1 If degA x   degP x , perform a division
  • 3. Integration By Partial Fractions  Ax To find;  dx P x  1 If degA x   degP x , perform a division 2 If degA x   degP x , factorise P x 
  • 4. Integration By Partial Fractions  Ax To find;  dx P x  1 If degA x   degP x , perform a division 2 If degA x   degP x , factorise P x  A a) for linear factor  x  a , write xa
  • 5. Integration By Partial Fractions  Ax To find;  dx P x  1 If degA x   degP x , perform a division 2 If degA x   degP x , factorise P x  A a) for linear factor  x  a , write xa b) for multiple linear factors  x  a  , write n A B C   x  a x  a 2  x  a n
  • 6. Integration By Partial Fractions  Ax To find;  dx P x  1 If degA x   degP x , perform a division 2 If degA x   degP x , factorise P x  A a) for linear factor  x  a , write xa b) for multiple linear factors  x  a  , write n A B C   x  a x  a 2  x  a n Ax  B c) for polynomial factors e.g. ax  bx  c, write 2 2 ax  bx  c
  • 8. x2 x e.g. i  dx x 1 x2  0x  0 x 1 x2  x
  • 9. x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x x0
  • 10. x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x x0  x 1
  • 11. x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x x0  x 1 1
  • 12. x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x   x 1 1     dx x  1 x0  x 1 1
  • 13. x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x   x 1 1     dx x  1 x0 1  x 1  x 2  x  log x  1  c 2 1
  • 14. x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x   x 1 1     dx x  1 x0 1  x 1  x 2  x  log x  1  c 2 1 3dx ii  x2  x
  • 15. x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x   x 1 1     dx x  1 x0 1  x 1  x 2  x  log x  1  c 2 1 3dx ii  x2  x 3dx  x x  1
  • 16. x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x   x 1 1     dx x  1 x0 1  x 1  x 2  x  log x  1  c 2 1 3dx A B 3 ii  2   x x x x  1 x x  1 3dx  x x  1
  • 17. x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x   x 1 1     dx x  1 x0 1  x 1  x 2  x  log x  1  c 2 1 3dx A B 3 ii    x2  x x x  1 x x  1  3dx A x  1  Bx  3 x x  1
  • 18. x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x   x 1 1     dx x  1 x0 1  x 1  x 2  x  log x  1  c 2 1 3dx A B 3 ii    x2  x x x  1 x x  1  3dx A x  1  Bx  3 x x  1 x0 A3 A  3
  • 19. x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x   x 1 1     dx x  1 x0 1  x 1  x 2  x  log x  1  c 2 1 3dx A B 3 ii    x2  x x x  1 x x  1  3dx A x  1  Bx  3 x x  1 x0 x 1 A3 B3 A  3
  • 20. x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x   x 1 1     dx x  1 x0 1  x 1  x 2  x  log x  1  c 2 1 3dx A B 3 ii    x2  x x x  1 x x  1  3dx A x  1  Bx  3 x x  1  3 3  x0 x 1     dx A3 B3  x  x  1 A  3
  • 21. x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x   x 1 1     dx x  1 x0 1  x 1  x 2  x  log x  1  c 2 1 3dx A B 3 ii    x2  x x x  1 x x  1  3dx A x  1  Bx  3 x x  1  3 3  x0 x 1     dx A3 B3  x  x  1  3 log x  3 log x  1  c A  3
  • 22. x2 x 1 e.g. i  dx x 1 x2  0x  0 x 1 x2  x   x 1 1     dx x  1 x0 1  x 1  x 2  x  log x  1  c 2 1 3dx A B 3 ii    x2  x x x  1 x x  1  3dx A x  1  Bx  3 x x  1  3 3  x0 x 1     dx A3 B3  x  x  1  3 log x  3 log x  1  c A  3 x  1  3 log  c  x 
  • 23. x5 iii  2 dx x  3 x  10
  • 24. x5 iii  2 dx x  3 x  10 x5  dx  x  5 x  2
  • 25. x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2
  • 26. x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2 x  2  7B  3 3 B 7
  • 27. x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2 x  2 x5  7B  3 7 A  10 3 10 B A 7 7
  • 28. x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2 x  2 x5  10 3   7B  3 7 A  10     dx  7  x  5  7  x  2  3 10 B A 7 7
  • 29. x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2 x  2 x5  10 3   7B  3 7 A  10     dx  7  x  5  7  x  2  3 10 10 3 B A  log x  5  log x  2   c 7 7 7 7
  • 30. x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2 x  2 x5  10 3   7B  3 7 A  10     dx  7  x  5  7  x  2  3 10 10 3 B A  log x  5  log x  2   c 7 7 7 7 dx iv  3 x x
  • 31. x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2 x  2 x5  10 3   7B  3 7 A  10     dx  7  x  5  7  x  2  3 10 10 3 B A  log x  5  log x  2   c 7 7 7 7 dx iv  3 x x dx  xx 2  1
  • 32. x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2 x  2 x5  10 3   7B  3 7 A  10     dx  7  x  5  7  x  2  3 10 10 3 B A  log x  5  log x  2   c 7 7 7 7 A Bx  C 1 iv  3 dx  2  x x x x  1 xx 2  1  dx Ax 2  1   Bx  C x  1 xx 2  1
  • 33. x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2 x  2 x5  10 3   7B  3 7 A  10     dx  7  x  5  7  x  2  3 10 10 3 B A  log x  5  log x  2   c 7 7 7 7 A Bx  C 1 iv  3 dx  2  x x x x  1 xx 2  1  dx Ax 2  1   Bx  C x  1 xx 2  1 x0 A 1
  • 34. x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2 x  2 x5  10 3   7B  3 7 A  10     dx  7  x  5  7  x  2  3 10 10 3 B A  log x  5  log x  2   c 7 7 7 7 A Bx  C 1 iv  3 dx  2  x x x x  1 xx 2  1  dx Ax 2  1   Bx  C x  1 xx 2  1 xi x0 A 1  B  Ci  1
  • 35. x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2 x  2 x5  10 3   7B  3 7 A  10     dx  7  x  5  7  x  2  3 10 10 3 B A  log x  5  log x  2   c 7 7 7 7 A Bx  C 1 iv  3 dx  2  x x x x  1 xx 2  1  dx Ax 2  1   Bx  C x  1 xx 2  1 xi x0 A 1  B  Ci  1 B  1 C  0
  • 36. x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2 x  2 x5  10 3   7B  3 7 A  10     dx  7  x  5  7  x  2  3 10 10 3 B A  log x  5  log x  2   c 7 7 7 7 A Bx  C 1 iv  3 dx  2  x x x x  1 xx 2  1  dx Ax 2  1   Bx  C x  1 xx 2  1 xi x0    1  x  dx  A 1  B  Ci  1  x x  1 2 B  1 C  0
  • 37. x5 x5 iii  2 dx A  B  x  3 x  10  x  5  x  2  x  5 x  2 x5  dx A x  2   B x  5  x  5  x  5 x  2 x  2 x5  10 3   7B  3 7 A  10     dx  7  x  5  7  x  2  3 10 10 3 B A  log x  5  log x  2   c 7 7 7 7 A Bx  C 1 iv  3 dx  2  x x x x  1 xx 2  1  dx Ax 2  1   Bx  C x  1 xx 2  1 xi x0    1  x  dx  A 1  B  Ci  1  x x  1 2 B  1 C  0  log x  logx 2  1  c 1 2
  • 38. xdx v   x  12 x 2  1
  • 39. v  xdx A B Cx  D x   2   x  12 x 2  1  x  1  x  12 x  1  x  12 x 2  1 A x  1x 2  1  B x 2  1  Cx  D  x  1  x 2
  • 40. v  xdx A B Cx  D x   2   x  12 x 2  1  x  1  x  12 x  1  x  12 x 2  1 A x  1x 2  1  B x 2  1  Cx  D  x  1  x 2 x  1 2 B  1 1 B 2
  • 41. v  xdx A B Cx  D x   2   x  12 x 2  1  x  1  x  12 x  1  x  12 x 2  1 A x  1x 2  1  B x 2  1  Cx  D  x  1  x 2 x  1 xi 2 B  1  2C  2 Di  i 1 B 2
  • 42. v  xdx A B Cx  D x   2   x  12 x 2  1  x  1  x  12 x  1  x  12 x 2  1 A x  1x 2  1  B x 2  1  Cx  D  x  1  x 2 x  1 xi 2 B  1  2C  2 Di  i 1 1 C 0 D B 2 2
  • 43. v  xdx A B Cx  D x   2   x  12 x 2  1  x  1  x  12 x  1  x  12 x 2  1 A x  1x 2  1  B x 2  1  Cx  D  x  1  x 2 x  1 xi 2 B  1  2C  2 Di  i 1 1 C 0 D B 2 2 x0 2A  B  D  0 1 1 2A    0 2 2 A0
  • 44. v  xdx A B Cx  D x   2   x  12 x 2  1  x  1  x  12 x  1  x  12 x 2  1 A x  1x 2  1  B x 2  1  Cx  D  x  1  x 2  1 x  1 xi 1      2 x  1 2x  1 2 2  dx 2 B  1  2C  2 Di  i 1 1 C 0 D B 2 2 x0 2A  B  D  0 1 1 2A    0 2 2 A0
  • 45. v  xdx A B Cx  D x   2   x  12 x 2  1  x  1  x  12 x  1  x  12 x 2  1 A x  1x 2  1  B x 2  1  Cx  D  x  1  x 2  1 x  1 xi 1      2 x  1 2x  1 2 2  dx 2 B  1  2C  2 Di  i 1 1 C 0 D 1  1  B 2     x  1  2 2 2  x  1 dx 2 x0 2A  B  D  0 1 1 2A    0 2 2 A0
  • 46. v  xdx A B Cx  D x   2   x  12 x 2  1  x  1  x  12 x  1  x  12 x 2  1 A x  1x 2  1  B x 2  1  Cx  D  x  1  x 2  1 x  1 xi 1      2 x  1 2x  1 2 2  dx 2 B  1  2C  2 Di  i 1 1 C 0 D 1  1  B 2     x  1  2 2 2  x  1 dx 2 x0 1    x  11 1  2A  B  D  0    tan x   c 2  1  1 1 2A    0 2 2 A0
  • 47. v  xdx A B Cx  D x   2   x  12 x 2  1  x  1  x  12 x  1  x  12 x 2  1 A x  1x 2  1  B x 2  1  Cx  D  x  1  x 2  1 x  1 xi 1      2 x  1 2x  1 2 2  dx 2 B  1  2C  2 Di  i 1 1 C 0 D 1  1  B 2     x  1  2 2 2  x  1 dx 2 x0 1    x  11 1  2A  B  D  0    tan x   c 2  1  1 1 2A    0 1 1  2 2    tan 1 x   c A0 2  x 1 
  • 48. v  xdx A B Cx  D x   2   x  12 x 2  1  x  1  x  12 x  1  x  12 x 2  1 A x  1x 2  1  B x 2  1  Cx  D  x  1  x 2  1 x  1 xi 1      2 x  1 2x  1 2 2  dx 2 B  1  2C  2 Di  i 1 1 C 0 D 1  1  B 2     x  1  2 2 2  x  1 dx 2 x0 1    x  11 1  2A  B  D  0    tan x   c 2  1  1 1 2A    0 1 1  Exercise 2G; 2 2    tan 1 x   c 1, 3, 5, 7 to 21 A0 2  x 1 