9n0

BLOQUE ALGEBRA Y FUNCIONES
Objetivos de la unidad
Establecer relaciones de orden en un conjunto de números racionales e irracionales , con el
empleo de la recta numérica (representación geométrica)
Aplicar propiedades algebraicas.
Expresar raíces como potencias con exponentes racionales.
Metodologia:
Aplique sus conocimiento a través de las situaciones cotidianas para resolver problemas de
su entornos aplicando leyes y reglas que faciliten su resolución.
Indicadores de logro.
Reconoce situaciones reales e las que se utilizan números racionales e reales.
Valor a practicar
La Honestidad.
UNIDAD UNO
TEMAS
 NUMEROS RACIONALES E IRRACIONALES
 NUMEROS REALES OPERACIONES
 NOTACION CIENTIFICA
 POTENCIAS, RAICES Y LOGARITMOS DE NUMEROS REALES .
 RESOLUCIÓN DE PROBLEMAS.

Definición de los números racionales
Los números se clasifican en cinco tipos principales: números naturales «N», números
enteros «Z», números racionales «Q», números reales «R» (incluyen a los irracionales) y
números complejos «C».
Los Números Racionales «Q» son aquellos que pueden expresarse como una fracción de
dos números enteros. Por ejemplo: Q = [¼, ¾, etc.]
Clasificación de números decimales
Decimales
finitos
Decimales infinitos
periódicos
Decimales infinitos
semiperiódicos
Decimales infinitos no
periódicos
Tienen una
cantidad
finita de
cifras
decimales.
Por ejemplo:
Inmediatamente
después de la coma
decimal hay una o más
cifras que se repiten
infinitamente
(período). Por ejemplo:
(período: 4).
Después de la coma
decimal hay una o
más cifras que se
repiten una cantidad
finita de veces
(anteperíodo) y
luego una o más
cifras que se repiten
infinitamente
(período). Por
ejemplo:
(anteperíodo: 14,
período: 25).
Después de la coma decimal
no presenta período ni
anteperíodo, es decir, las cifras
decimales no tienen un patrón
de repetición. Por ejemplo:
Notación. Por convención, las cifras que constituyen el período se simbolizan con una
«barra» sobre ellas. Por ejemplo:
Expresiónes fraccionarias de números decimales
Se deben considerar tres casos:
 Número decimal finito.
 Número decimal infinito periódico.
 Número decimal infinito semiperiódico.

Los números decimales infinitos no periódicos no pueden expresarse de la forma , por lo
tanto, no son números racionales.
Expresión fraccionaria de un número decimal finito
Se debe amplificar el número decimal por una potencia de 10 que tenga tantos ceros como
cifras tenga la parte decimal del número.
Ejemplos:
Expresión fraccionaria de un número decimal infinito periódico
En el numerador se escribe la diferencia entre el número decimal, sin la coma, y el número
que aparece en la parte entera; y en el denominador, se escriben tantos 9 como cifras tenga
el período.
Ejemplos:
Si un decimal infinito periódico o semiperiódico tiene el período formado exclusivamente
por nueves, entonces este decimal es igual a un número entero o a un número decimal
finito.
Ejemplo:

Expresiones irreductibles
La expresión es irreductible si y solo si a y b tienen como único divisor común al 1. Para
obtener una expresión irreductible, se debe simplificar por el m.c.d. de a y b.

Representación de números racionales en la recta numérica.
Recordemos que el conjunto de los números enteros se denota por y se define de
la manera siguiente:
Podemos representar los números enteros como puntos de una recta de la manera
siguiente:
El segmento de recta comprendido entre dos números enteros consecutivos se llama
"segmento unidad".
De manera similar, recordemos que el conjunto de los números racionales se denota
por y se define de la manera siguiente:
Debido a que si , , entonces se cumple que ; se
conviene en representar los números racionales preferentemente por medio de
fracciones en las cuales el denominador es un número entero positivo.
Recordemos además que si , , , el número racional se puede
considerar como el cociente que se obtiene al dividir por ; en donde indica el
número de partes en que se divide la unidad y el número de partes que se toman.
De esta manera, si se divide en dos partes iguales cada segmento unidad en la recta
numérica, podemos representar los números racionales cuya representación
fraccionaria tiene como denominador 2, como se muestra en el ejemplo siguiente.

Ejemplo
Represente en la recta numérica los siguientes números racionales:
a. b. c. d.
Solución:
De igual manera, si se dividen en tres partes iguales cada segmento unidad en la
recta, podemos representar los números racionales cuya representación fraccionaria
tiene como denominador 3, como se muestra en el ejemplo siguiente.
Ejemplo
Represente en la recta numérica los siguientes números racionales:
a. b. c. d.
Solución:
Generalizando el procedimiento descrito anteriormente se puede representar
cualquier número racional en la recta numérica.

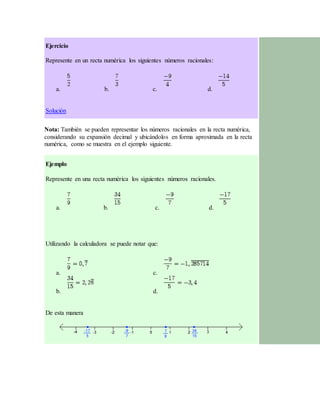
Ejercicio
Represente en un recta numérica los siguientes números racionales:
a. b. c. d.
Solución
Nota: También se pueden representar los números racionales en la recta numérica,
considerando su expansión decimal y ubicándolos en forma aproximada en la recta
numérica, como se muestra en el ejemplo siguiente.
Ejemplo
Represente en una recta numérica los siguientes números racionales.
a. b. c. d.
Utilizando la calculadora se puede notar que:
a.
b.
c.
d.
De esta manera

Ejercicios
1. Represente en una recta numérica los siguientes números racionales.
a.
a. b. c. d.
b.
d. b. c. d.
2. Utilice la calculadora para encontrar la expansión decimal de los siguientes
números racionales y represéntelos en una recta numérica.
a.
d. b. c. d.
b.
d. b. c. d.
Solución
RUBRICA DE EVALUACIÓN
1.- Luegode la Caratula trascribael objetivode launidad,lostemasadesarrollarque
se exponenenlaparte de arriba.

2.- Elabore unmapa conceptual conla informacióndetalladaanteriormente sobre el tema
númerosracionales yexpresionesdecimales (6puntos)
3.- Resuelvalosejerciciospropuestosacontinuación (4puntos)
Todas estas actividadesdetallasanteriormentedebe realizarlasenparte de materia

9n0

Más contenido relacionado

La actualidad más candente (19)

Similar a 9n0 (20)

Último (20)

9n0