Grafos

Universidad Fermín Toro
Vicerrectorado Académico
Facultad de Ingeniería
Escuela de Computación
GRAFOS
Luis Ovalle
C.I 27.937.532

Dado el siguiente grafo, encontrar:
a) Matriz de adyacencia
b) Matriz de incidencia
c) Es conexo? Justifique su respuesta
d) Es simple? Justifique su respuesta
e) Es regular justifique su respuesta
f) Es completo? Justifique su
respuesta
g) Una cadena simple no elemental
de grado 6
h) Un ciclo no simple de grado 5
i) Árbol generador aplicando el
algoritmo constructor
j) Subgrafo parcial
k) Demostrar si es euleriano
aplicando el algoritmo de Fleury
l) Demostrar si es Hamiltoniano

V1 V2 V3 V4 V5 V6 V7 V8
V1 0 1 1 1 0 0 1 1
V2 1 0 1 0 1 1 0 1
V3 1 1 0 1 1 1 1 0
V4 1 0 0 0 0 1 1 1
V5 0 1 1 1 0 1 1 1
V6 0 1 1 0 1 0 0 1
V7 1 0 1 1 1 0 0 1
V8 1 1 0 0 1 1 1 0
A) Matriz de Adyacencia

a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 a14 a15 a16 a17 a18 a19 a20
V1 1 1 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
V2 1 0 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0
V3 0 1 1 0 0 0 0 1 0 0 1 1 1 0 0 0 0 0 0 0
V4 0 0 0 1 0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0
V5 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 1 1 0 1 0
V6 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 0 1
V7 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 0 1 1 0 0
V8 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 1 1
B) Matriz de incidencia

C) Es conexo? Justifique su respuesta
R: Si, es conexo, ya que todos sus vértices están
conectados entre si.
D) Es simple? Justifique su respuesta
R: No, en el grafo dado hay hasta 4 aristas, unen a un
vértices y para que fuera arista solo una de las aristas
esta uniendo a 2 vértices cualquieras.
E) Es regular? Justifique su respuesta
R: No, para que sea regular cada vértice tiene que
tener el mismo grado o valencia, en el grafo del
ejercicio dado se puede ver que los vértices no
comparten esa similitud.

F) Es completo? Justifique su respuesta
R: No, para que un grafo sea completo todas las aristas
tienen que estar conectadas a cada vértice.
G) Una cadena simple no elemental de grado 6
R: C=(V1,a4,V4,a11,V3,A3,V2,a8,V5,a13,V3,a18).
H) Un ciclo no simple de grado 5
R: C=(V1,a1,V2,a10,V6,a7,V3,a3,V2,a1,V1)

I)Árbol generador aplicando el algoritmo
constructor

H1= {1} se escoge a5.
H2= {V1, V7} se escoge a12.
H3= {V1, V7, V3} se escoge a3.
H4= {V1, V7, V3, V2} se escoge a10.
H5= {V1, V7, V3, V2, V4} se escoge a20.
H6= {V1, V7, V3, V2, V4, V8} se escoge a19.
H7= {V1, V7, V3, V2, V4, V8, V5} se escoge a12.
H8= {V1, V7, V3, V2, V4, V8, V5, V6} se escoge a14

K) Demostrar si es eureliano aplicando el
algoritmo de Fleury
Se concluyo que el grafo no es eureliano, ya que al
aplicarse el algoritmo de Fleury y partiendo desde
cualquier vértice no es posible obtener un ciclo
eureliano

L) Demostrar si es hamiltoniano
Se demostró que si es hamiltoniano, ya que se obtuvo
una cadena con un ciclo hamiltoniano:
C=[V1, a1, V2, a3, V3, a11, V6, a14, V5, a16, V4, a20,
V8, a18, V7, a5, V1].

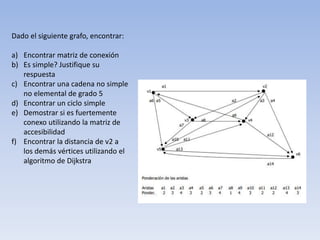
Dado el siguiente grafo, encontrar:
a) Encontrar matriz de conexión
b) Es simple? Justifique su
respuesta
c) Encontrar una cadena no simple
no elemental de grado 5
d) Encontrar un ciclo simple
e) Demostrar si es fuertemente
conexo utilizando la matriz de
accesibilidad
f) Encontrar la distancia de v2 a
los demás vértices utilizando el
algoritmo de Dijkstra

V1 V2 V3 V4 V5 V6
V1 0 1 1 0 1 0
V2 0 0 1 1 0 1
V3 0 0 0 1 1 0
V4 1 0 0 0 0 1
V5 0 1 0 1 0 1
V6 0 0 0 0 1 0
A) Encontrar matriz de conexión

B) Es simple? Justifique su respuesta
El dígrafo es simple ya que no tiene ningún lazo
y tampoco existen arcos paralelos que partan de
un mismo vértice a otro.

C) Encontrar una cadena simple.
T=[V1, a1, V2, a2, V3, a8, V4, a9, V1, a1, V2]
D) Encontrar un ciclo simple.
C=[V6, a14, V5, a11, V4, a12, V6]

0 1 1 0 1 0
0 0 1 1 1 0
MC 0 0 0 1 1 0
1 0 0 0 0 1
0 1 0 1 0 1
0 0 0 0 1 0
0 1 1 1 1 1 1 1 1 1 1 1
1 1 0 1 1 1 1 1 1 1 1 1
M2 1 1 0 1 0 1 M3 1 1 1 1 1 1
0 1 1 0 1 0 0 1 1 1 1 1
1 0 1 1 1 1 1 1 1 1 1 1
0 1 0 1 0 1 1 0 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1
M4 1 1 1 1 1 1 M5 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1
1 0 0 0 0 0
0 1 0 0 0 0
M1 0 0 1 0 0 0
0 0 0 1 0 0
0 0 0 0 1 0
0 0 0 0 0 1
4 5 5 4 5 4 1 1 1 1 1 1
4 5 4 5 5 4 1 1 1 1 1 1
ACC(D)=bin 4 4 4 5 4 4 ACC(D)= 1 1 1 1 1 1
3 4 4 4 4 4 1 1 1 1 1 1
4 4 4 5 5 5 1 1 1 1 1 1
3 3 3 4 4 5 1 1 1 1 1 1
E) Demostrar si es fuertemente
conexo utilizando la matriz de
accesibilidad

F) Encontrar la distancia de V2 a los demás
vértices utilizando el algoritmo de dijkstra

• F) Encontrar la distancia de V2 a los demás

F) Encontrar la distancia de V2 a los demás
De V2 a V1=8
De V2 a V3=3
De V2 a V4=4
De V2 a V5=6
De V2 a V6=3

Grafos

Más contenido relacionado

La actualidad más candente (20)

Similar a Grafos (20)

Último (20)

Grafos