Tarea 7 mate

FACULTAD
CIENCIAS HUMANAS, DE LA EDUCACIÓN Y DESARROLLO SOCIAL CARRERA
EDUCACIÓN BÁSICA
MODULO
VII
DOMINIO DEL CONOCIMIENTO MATEMATICO
TEMA:
EXPLICA LOS ELEMENTOS DE PRUEBAS DE HIPOTESIS UNILATERALES.
PARALELO 03
ESTUDIANTE:
RAUL PAREDES

• Al realizar pruebas de hipótesis, se parte de un valor supuesto
(hipotético) en parámetro poblacional. Después de recolectar una
muestra aleatoria, se compara la estadística muestral, así como la
media (x), con el parámetro hipotético, se compara con una supuesta
media poblacional (). Después se acepta o se rechaza el valor
hipotético, según proceda. Se rechaza el valor hipotético sólo si el
resultado muestral resulta muy poco probable cuando la hipótesis es
cierta.

Etapa 1.- Planear la hipótesis nula y
la hipótesis alternativa. La hipótesis
nula (H0) es el valor hipotético del
parámetro que se compra con el
resultado muestral resulta muy poco
probable cuando la hipótesis es
cierta.
Etapa 2.- Especificar el nivel de
significancia que se va a utilizar. El
nivel de significancia del 5%,
entonces se rechaza la hipótesis nula
solamente si el resultado muestral es
tan diferente del valor hipotético que
una diferencia de esa magnitud o
mayor, pudiera ocurrir aleatoria
mente con una probabilidad de 1.05
o menos.
Etapa 3.- Elegir la estadística de prueba. La estadística
de prueba puede ser la estadística muestral (el
estimador no segado del parámetro que se prueba) o
una versión transformada de esa estadística muestral.
Por ejemplo, para probar el valor hipotético de una
media poblacional, se toma la media de una muestra
aleatoria de esa distribución normal, entonces es
común que se transforme la media en un valor z el
cual, a su vez, sirve como estadística de prueba.
Etapa 4.- Establecer el valor o valores críticos de la
estadística de prueba. Habiendo especificado la
hipótesis nula, el nivel de significancia y la
estadística de prueba que se van a utilizar, se
produce a establecer el o los valores críticos de
estadística de prueba. Puede haber uno o más de
esos valores, dependiendo de si se va a realizar
una prueba de uno o dos extremos.
Etapa 5.- Determinar el valor real de la estadística de
prueba. Por ejemplo, al probar un valor hipotético de
la media poblacional, se toma una muestra aleatoria y
se determina el valor de la media muestral. Si el valor
crítico que se establece es un valor de z, entonces se
transforma la media muestral en un valor de z.
Etapa 6.- Tomar la decisión. Se compara el valor
observado de la estadística muestral con el valor
(o valores) críticos de la estadística de prueba.
Después se acepta o se rechaza la hipótesis nula.
Si se rechaza ésta, se acepta la alternativa; a su
vez, esta decisión tendrá efecto sobre otras
decisiones de los administradores operativos,
como por ejemplo, mantener o no un estándar de
desempeño o cuál de dos estrategias de
mercadotecnia utilizar.

PASOS DE LA PRUEBA DE HIPÓTESIS
1. Expresar la hipótesis nula
2. Expresar la hipótesis alternativa
3. Especificar el nivel de significancía
4. Determinar el tamaño de la muestra
5. Establecer los valores críticos que establecen las regiones de rechazo de las de no rechazo.
6. Determinar la prueba estadística.
7. Coleccionar los datos y calcular el valor de la muestra de la prueba estadística apropiada.
8. Determinar si la prueba estadística ha sido en la zona de rechazo a una de no rechazo.
9. Determinar la decisión estadística.
10. Expresar la decisión estadística en términos del problema.

Prueba de hipótesis direccionada, de una cola o
unilateral
En este caso, a diferencia del anterior, sí estamos interesados en determinar si el valor del estimador (muestra) es
mayor o menor que el valor del parámetro (e.g. μ). Por esta razón este tipo de prueba se denomina también de una
cola o unilateral; ya que Ho se rechazará si el valor del estadístico de prueba se ubica en la cola inferior o superior de
la distribución muestral como se ilustra a continuación:

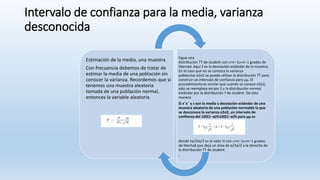
Intervalo de confianza para la media, varianza
desconocida
Estimación de la media, una muestra
Con frecuencia debemos de tratar de
estimar la media de una población sin
conocer la varianza. Recordemos que si
tenemos una muestra aleatoria
tomada de una población normal,
entonces la variable aleatoria.
Sigue una
distribución TT de student con υ=n−1υ=n−1 grados de
libertad. Aquí S es la desviación estándar de la muestra.
En el caso que no se conozca la varianza
poblacinal σ2σ2 se puede utilizar la distribución TT para
construir un intervalo de confianza para μμ. El
procedimiento es similar que cuando se conoce σ2σ2,
sólo se reemplaza σσ por S y la distribución normal
estándar por la distribución T de student. De esta
manera
Si x¯x¯ y s son la media y desviación estándar de una
muestra aleatoria de una población normalde la que
se desconoce la varianza σ2σ2, un intervalo de
confianza del 100(1−α)%100(1−α)% para μμ es
donde tα/2tα/2 es el valor tt con υ=n−1υ=n−1 grados
de libertad que deja un área de α/2α/2 a la derecha de
la distribución TT de student.
:

• Ejemplo de Varianza
• Para calcular la varianza, primero se debe calcular la media o el promedio de los datos usados. Por
otro lado, si se tiene la desviación estándar, simplemente se eleva al cuadrado ese resultado y así
se obtiene la varianza.
• A continuación, se muestra un ejemplo para entender cómo se calcula la varianza y cuál podría ser
su interpretación.
• Supongamos que se tienen los ingresos anuales de cinco empresas distintas, pertenecientes a un
mismo empresario, los cuales son:
• • Empresa A: 2.500 $
• • Empresa B: 1.800 $
• • Empresa C: 2.300 $
• • Empresa D: 3.000 $
• • Empresa E: 2.700 $
• Entonces calculamos la media de los ingresos, simplemente sumando cada cifra y dividiéndolo
entre el número total de empresas, lo cual da como resultado: 2.460$.
• Ahora simplemente terminamos de calcular la varianza con la formula ya expuesta, lo cual da
como resultado una varianza de 162.400 $2.
• Al sacar la raíz cuadrada a este resultado obtenemos la desviación estándar, siendo ésta 403 $ de
diferencia entre los ingresos de las cinco empresas.

• Pruebas bilaterales y pruebas unilaterales
• Un contraste bilateral adopta en general la forma:
• H0: θ = θ0 contra H1: θ ≠ θ0
• En determinadas ocasiones el experimentador prefiere plantear directamente un contraste de la forma:
• H0: θ = θ0 contra H1: θ > θ0
• conocido como contraste unilateral derecho. Obviamente, otra posibilidad es el unilateral izquierdo:
• H0: θ = θ0 contra H1: θ < θ0
• En estos tres casos, el contraste de hipótesis es simple contra compuesta.
• En la mayoría de situaciones aplicadas, se desean realmente resolver contrastes unilaterales que comportan hipótesis
compuestas. El unilateral derecho es entonces:
• H0: θ ≤ θ0 contra H1: θ > θ0
• y el izquierdo es:
• H0: θ ≥ θ0 contra H1: θ < θ0
• Aunque esta última formulación está relacionada con los contrastes unilaterales simple contra compuesta anteriores, las
dos hipótesis no son técnicamente equivalentes Para simplificar la interpretación de los contrastes unilaterales,
atendiendo a los casos de los que se ocupa Statmedia, se formulan los contrastes de esta última manera (compuesta
contra compuesta) y se toma el nivel de significación como si fuera el del contraste simple contra compuesta.
• En cualquier caso, es importante entender que sólo debe resolverse uno de los tres contrastes (bilateral o unilateral) con
un conjunto de datos concreto.
• Por ejemplo, es incorrecto desde el punto de vista metodológico empezar contrastando bilateralmente, y hacer luego un
test unilateral. El contraste que se ha de emplear debe decidirse basándose en conocimientos previos del problema, o
bien guiándose por la cuestión de interés aplicado a responder.

Tarea 7 mate

Más contenido relacionado

La actualidad más candente (20)

Similar a Tarea 7 mate (20)

Último (20)

Tarea 7 mate