Introduction to Matrix Factorization Methods Collaborative Filtering
52 likes19,419 views
The document outlines the process of matrix factorization for predicting user ratings using collaborative filtering methods, with a focus on minimizing cost functions and learning preference factor vectors. It discusses the importance of handling missing data effectively, the advantages of using matrix factorization over standard singular value decomposition (SVD), and provides implementation steps for developing the model. Additionally, it emphasizes the significance of regularization to prevent model overfitting and offers insights into tuning model parameters.
Introduction to Matrix Factorization Methods Collaborative Filtering
- 1. INTRODUCTION TO MATRIX FACTORIZATION proprietary material METHODS COLLABORATIVE FILTERING USER RATINGS PREDICTION 1 Alex Lin Senior Architect Intelligent Mining
- 2. Outline Factoranalysis Matrix decomposition proprietary material Matrix Factorization Model Minimizing Cost Function Common Implementation 2
- 3. Factor Analysis Aprocedure can help identify the factors that might be used to explain the interrelationships among the variables proprietary material Model based approach 3
- 4. Refresher: Matrix Decomposition r q p 5 x 6 matrix 5 x 3 matrix 3 x 6 matrix X11 X12 X13 X14 X15 X16 x proprietary material X21 X22 X12 X24 X25 X26 y X31 X32 X33 X34 X35 X36 a b c z X41 X42 X43 X44 X45 X46 X51 X52 X53 X54 X55 X56 X32 = (a, b, c) . (x, y, z) = a * x + b * y + c * z Rating Prediction rui = qT pu ˆ i User Preference Factor Vector 4 Movie Preference Factor Vector
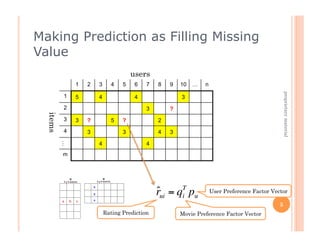
- 5. Making Prediction as Filling Missing Value users 1 2 3 4 5 6 7 8 9 10 … n proprietary material 1 5 4 4 3 2 3 ? items 3 3 ? 5 ? 2 4 3 3 4 3 4 4 … m rui = qT pu ˆ i User Preference Factor Vector 5 Rating Prediction Movie Preference Factor Vector €
- 6. Learn Factor Vectors users 1 2 3 4 5 6 7 8 9 10 … n 1 5 4 4 3 proprietary material 2 3 ? items 3 3 ? 5 ? 2 4 3 3 4 3 4 4 … 4 = U3-1 * I1-1 + U3-2 * I1-2 + U3-3 * I1-3 + U3-4 * I1-4 m 3 = U7-1 * I2-1 + U7-2 * I2-2 + U7-3 * I2-3 + U7-4 * I2-4 ….. 3 = U86-1 * I12-1 + U86-2 * I12-2 + U86-3 * I12-3 + U86-4 * I12-4 Note: only train on known entries 2X + 3Y = 5 2X + 3Y = 5 6 4X - 2Y = 2 4X - 2Y = 2 3X - 2Y = 2
- 7. Why not use standard SVD? Standard SVD assumes all missing entries are zero. This leads to bad prediction accuracy, especially when dataset is extremely sparse. (98% proprietary material - 99.9%) See Appendix for SVD In some published literatures, they call Matrix Factorization as SVD, but note it’s NOT the same kind of classical low-rank SVD produced by svdlibc. 7
- 8. How to Learn Factor Vectors How do we learn preference factor vectors (a, b, c) and (x, y, z)? proprietary material Minimize errors on the known ratings To learn the factor min q*. p* ∑ (rui − x ui ) 2 vectors (pu and qi) (u,i)∈k Minimizing Cost Function (Least Squares Problem) rui : actual rating for user u on item I € xui : predicted rating for user u on item I 8
- 9. Data Normalization Remove Global mean users proprietary material 1 2 3 4 5 6 7 8 9 10 … n 1 1.5 -.9 -.2 .49 2 .79 ? items 3 0.6 ? .46 ? -.4 4 .39 .82 .76 .69 … .52 .8 m 9
- 10. Factorization Model Only Preference factors min ∑ (rui − µ − qT pu ) 2 proprietary material i q*. p* (u,i)∈k To learn the factor vectors (pu and qi) Rating = 4 € Global Preference Mean Factor rui : actual rating of user u on item I u : training rating average bu : user u user bias 10 bi : item i item bias qi : latent factor array of item i pu : later factor array of user u
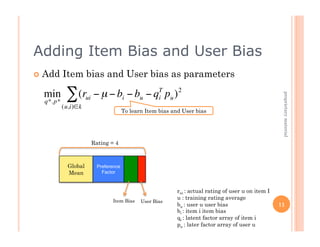
- 11. Adding Item Bias and User Bias Add Item bias and User bias as parameters min ∑ (rui − µ − bi − bu − qT pu ) 2 proprietary material i q*. p* (u,i)∈k To learn Item bias and User bias Rating = 4 € Global Preference Mean Factor rui : actual rating of user u on item I u : training rating average Item Bias User Bias bu : user u user bias 11 bi : item i item bias qi : latent factor array of item i pu : later factor array of user u
- 12. Regularization To prevent model overfitting 2 2 ∑ proprietary material min (rui − µ − bi − bu − q pu ) + λ ( qi + pu + bi2 + bu ) T i 2 2 q*. p* (u,i)∈k Regularization to prevent overfitting Rating = 4 Global Preference Mean Factor rui : actual rating of user u on item I u : training rating average bu : user u user bias Item Bias User Bias bi : item i item bias 12 qi : latent factor array of item i pu : later factor array of user u λ : regularization Parameters €
- 13. Optimize Factor Vectors Find optimal factor vectors - minimizing cost function proprietary material Algorithms: Stochastic gradient descent Others: Alternating least squares etc.. Most frequently use: Stochastic gradient descent 13
- 14. Matrix Factorization Tuning Number of Factors in the Preference vectors Learning Rate of Gradient Descent proprietary material Best result usually coming from different learning rate for different parameter. Especially user/item bias terms. Parameters in Factorization Model Time dependent parameters Seasonality dependent parameters Many other considerations ! 14
- 15. High-Level Implementation Steps Construct User-Item Matrix (sparse data structure!) Define factorization model - Cost function proprietary material Take out global mean Decide what parameters in the model. (bias, preference factor, anything else? SVD++) Minimizing cost function - model fitting Stochastic gradient descent Alternating least squares Assemble the predictions Evaluate predictions (RMSE, MAE etc..) Continue to tune the model 15
- 16. Thank you Any question or comment? proprietary material 16
- 17. Appendix Stochastic Gradient Descent Batch Gradient Descent proprietary material Singular Value Decomposition (SVD) 17
- 18. Stochastic Gradient Descent Repeat Until Convergence { for i=1 to m in random order { proprietary material θ j := θ j + α (y (i) − hθ (x ( i) ))x (ji) (for every j) } partial derivative term } € Your code Here: 18
- 19. Batch Gradient Descent Repeat Until Convergence { m θ j := θ j + α ∑ (y (i) − hθ (x ( i) ))x (ji) (for every j) proprietary material i=1 partial derivative term } € Your code Here: 19
- 20. Singular Value Decomposition (SVD) A = U × S ×VT A U S VT m x r matrix r x r matrix r x n matrix proprietary material m x n matrix € items items rank = k k<r users users Ak = U k × Sk × VkT 20 €