The dynamic interaction of passed and failed requirements during software testing
0 likes479 views
The document explores a model for understanding the dynamic interaction of passed (ISR) and failed (FSR) requirements during software testing, highlighting the probabilities of failure and fixing. It introduces a transition probability matrix to predict changes in requirement states over time and analyzes steady state probabilities through Markov chains. The findings suggest constraints and upper limits on the probability of maintaining non-failed requirements, emphasizing the impact of initial failure rates and fixing rates on long-term outcomes.
![Steady State Analysis
• We are interested in knowing in the long run,
the probability P1 that any given requirement
will be in the ISR set. The probability that such
requirement will be in the FSR set is P2=1-P1.
• Markov chains can help us solve this problem
by calculating the Steady State probabilities of
Matrix M:
P1 = SFXR/(SFR+SFXR) [e1]
P2 =1- SFXR/(SFR+SFXR) [e2]
Copyrights (c) 2011-2013 Pragmatic
12
Cohesion Consulting](https://image.slidesharecdn.com/thedynamicinteractionofpassedandfailedrequirementsduringsoftwaretesting-130212153643-phpapp02/85/The-dynamic-interaction-of-passed-and-failed-requirements-during-software-testing-12-320.jpg)
![Steady State Analysis- Example 1
• if:
P1 = SFXR/(SFR+SFXR) [e1]
• Then P1 = 0.5 = 50% when SFR = SFXR.
• This implies that even if there is a low
probability that a requirement that has been
implemented fails testing (SFR); if an equally
low fixing rate takes place, given sufficient
time, a requirement gets closer and closer to
having a 50% chance of being in the set that
failed testing!
Copyrights (c) 2011-2013 Pragmatic
13
Cohesion Consulting](https://image.slidesharecdn.com/thedynamicinteractionofpassedandfailedrequirementsduringsoftwaretesting-130212153643-phpapp02/85/The-dynamic-interaction-of-passed-and-failed-requirements-during-software-testing-13-320.jpg)
![Steady State Analysis – Example 2
• From [e1] we can say that:
[e1] -> 0.9 = SFXR/(0.2+SFXR)
[e1] -> 0.9.(0.2+SFXR) = SFXR
[e1] -> 0.18 + 0.9.SFXR = SFXR
[e1] -> 0.18/(1-0.9) = SFXR
[e1] -> SFXR = 1.8 > 1 which is impossible!
Copyrights (c) 2011-2013 Pragmatic
15
Cohesion Consulting](https://image.slidesharecdn.com/thedynamicinteractionofpassedandfailedrequirementsduringsoftwaretesting-130212153643-phpapp02/85/The-dynamic-interaction-of-passed-and-failed-requirements-during-software-testing-15-320.jpg)
The dynamic interaction of passed and failed requirements during software testing
- 1. The dynamic interaction of passed and failed requirements during software testing Copyrights (c) 2011-2013 Pragmatic 1 Cohesion Consulting
- 2. Motivation • In my professional experience, I have repeatedly witnessed systemic issues during Software Verification that prompted me to develop the model presented in this paper. • It is my hope that the non-intuitive results that the model yields help software development team better understand certain dynamic behavior embedded in the software development process. Copyrights (c) 2011-2013 Pragmatic 2 Cohesion Consulting
- 3. Requirements Statuses • We are interested in 2 simple sets of requirements. All requirements within each set share one of the following statuses: – The first one represents requirements that have been implemented i.e. requirements for which the development team has created actual software code. Let’s call this set of requirements ISR. – The second one represents requirements that have failed testing after they were implemented by the development team. Let’s call this second set of requirements FSR. Copyrights (c) 2011-2013 Pragmatic 3 Cohesion Consulting
- 4. Requirement States Probabilities • Let’s call SFR the probability that a requirement that has been implemented fails testing. When this failure happens the requirement becomes part of the FSR set otherwise it remains in the ISR set. • Let’s call SFXR the probability that a failed requirement gets fixed. When the fix takes place, the requirement is no longer part of the FSR set but it moves into the ISR set. Copyrights (c) 2011-2013 Pragmatic 4 Cohesion Consulting
- 5. Requirement States Probabilities • The following probability constraints exist: 0 <= SFR <= 1 0 <= SFXR <=1 • We can derive a probability transition matrix that captures the possible transitions of a requirement from one set to the other: From ISR to ISR, probability = 1-SFR From ISR to FSR, probability = SFR From FSR to ISR, probability = SFXR From FSR to FSR, probability = 1-SFXR Copyrights (c) 2011-2013 Pragmatic 5 Cohesion Consulting
- 6. Transition probability matrix Let M be the transition probability matrix, M= To ISR To FSR From ISR 1-SFR SFR From FSR SFXR 1-SFXR Copyrights (c) 2011-2013 Pragmatic 6 Cohesion Consulting
- 7. Two-Step Transition probabilities • The following question is particularly interesting: – given the transition probability matrix M and the fact that a requirement has been added to the ISR set, what is the probability that this same requirement will be in the ISR set two transitions in the future? Copyrights (c) 2011-2013 Pragmatic 7 Cohesion Consulting
- 8. Two-Step Transition probabilities • The problem is not as obvious as it seems; here is is why: – When a Requirement enters set ISR it has a SFR probability of being moved to set FSR and a 1-SFR probability of staying in ISR. Once in FSR, it has a SFXR probability of moving into ISR and a 1-SFXR probability of staying in FSR. – We can represent the possible paths with the following tree Copyrights (c) 2011-2013 Pragmatic 8 Cohesion Consulting
- 9. Two-Step Transition probabilities ISR P(ISR,ISR,ISR) = (1-SFR).(1-SFR) 1-SFR ISR SFR 1-SFR FSR P(ISR,ISR,FSR) = (1-SFR).SFR ISR ISR P(ISR,FSR,ISR) = SFR.SFXR SFR SFXR FSR 1-SFXR FSR P(ISR,FSR,FSR) = SFR.(1-SFXR) Copyrights (c) 2011-2013 Pragmatic 9 Cohesion Consulting
- 10. Two-Step Transition probabilities • So the probability that a Requirement that started in ISR is in ISR after two transitions is: P(ISR,ISR,ISR) + P(ISR,FSR,ISR) = (1-SFR).(1-SFR) + SFR.SFRX • All other similar two-step transition probabilities can be calculated by M2 Copyrights (c) 2011-2013 Pragmatic 10 Cohesion Consulting
- 11. Two-Step Transition probabilities M2 = To ISR To FSR From ISR (1-SFR).(1-SRF)+SFR.SFXR (1-SFR).SFR+SRF.(1-SFXR) From FSR SFXR.(1-SFR)+(1-SFXR).SFXR SFXR.SFR+(1-SFXR).(1-SFXR) Copyrights (c) 2011-2013 Pragmatic 11 Cohesion Consulting
- 12. Steady State Analysis • We are interested in knowing in the long run, the probability P1 that any given requirement will be in the ISR set. The probability that such requirement will be in the FSR set is P2=1-P1. • Markov chains can help us solve this problem by calculating the Steady State probabilities of Matrix M: P1 = SFXR/(SFR+SFXR) [e1] P2 =1- SFXR/(SFR+SFXR) [e2] Copyrights (c) 2011-2013 Pragmatic 12 Cohesion Consulting
- 13. Steady State Analysis- Example 1 • if: P1 = SFXR/(SFR+SFXR) [e1] • Then P1 = 0.5 = 50% when SFR = SFXR. • This implies that even if there is a low probability that a requirement that has been implemented fails testing (SFR); if an equally low fixing rate takes place, given sufficient time, a requirement gets closer and closer to having a 50% chance of being in the set that failed testing! Copyrights (c) 2011-2013 Pragmatic 13 Cohesion Consulting
- 14. Steady State Analysis – Example 2 • Let’s look at another illustration: – P1 is the probability of having in the long run, a non-failed requirement. Let’s say that we want P1 to be 90%. If we know that an implemented requirement has an SFR=20% probability of failing testing then what should SFXR (the rate at which failed requirements are fixed) be to assure P1=90%? Copyrights (c) 2011-2013 Pragmatic 14 Cohesion Consulting
- 15. Steady State Analysis – Example 2 • From [e1] we can say that: [e1] -> 0.9 = SFXR/(0.2+SFXR) [e1] -> 0.9.(0.2+SFXR) = SFXR [e1] -> 0.18 + 0.9.SFXR = SFXR [e1] -> 0.18/(1-0.9) = SFXR [e1] -> SFXR = 1.8 > 1 which is impossible! Copyrights (c) 2011-2013 Pragmatic 15 Cohesion Consulting
- 16. Steady State Analysis – Example 2 • If SFXR was equal to its maximum value of 100% then the maximum value of P1 can only be 1/(1+0.2) = 83.3%=P1 • This result shows that there is a clear upper bound to the probability that in the long run a requirement will not fail testing given the value of SFR. SFR is the probability that a given requirement that has just been implemented fails testing. Copyrights (c) 2011-2013 Pragmatic 16 Cohesion Consulting
- 17. Steady State Analysis – Example 2 • The only way to achieve P1 = 90% when SFXR = 100% is to decrease SFR from 20% so that: 0.9 = 1/(SFR+1) SFR + 1 = 1/0.9 SFR = 1/0.9 – 1 SFR = 11.11% • This lower value of SFR implies a better quality of software code that properly implements more requirements. Copyrights (c) 2011-2013 Pragmatic 17 Cohesion Consulting
- 18. Transient Analysis • It is possible to graph the values of P1 and P2 over several transitions, this is called transient analysis. • Transient analysis can show how fast the steady states values for P1 and P2 are reached. • Transient analysis can also show instability in P1 and P2 values over several transitions due to higher values of SFR and SFRX (see examples 4 and 5 in subsequent slides). Copyrights (c) 2011-2013 Pragmatic 18 Cohesion Consulting
- 19. Transient Analysis – Example 1 • SFR = 10% and SFXR = 50% Copyrights (c) 2011-2013 Pragmatic 19 Cohesion Consulting
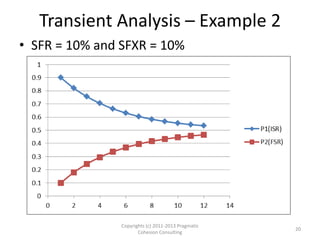
- 20. Transient Analysis – Example 2 • SFR = 10% and SFXR = 10% Copyrights (c) 2011-2013 Pragmatic 20 Cohesion Consulting
- 21. Transient Analysis – Example 3 • SFR = 10% and SFXR = 1% Copyrights (c) 2011-2013 Pragmatic 21 Cohesion Consulting
- 22. Transient Analysis – Example 4 • SFR = 90% and SFXR = 90% Copyrights (c) 2011-2013 Pragmatic 22 Cohesion Consulting
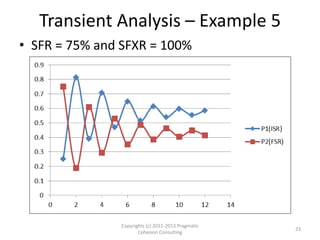
- 23. Transient Analysis – Example 5 • SFR = 75% and SFXR = 100% Copyrights (c) 2011-2013 Pragmatic 23 Cohesion Consulting
- 24. For Comments and Questions contact didier@pragmaticohesion.com Copyrights (c) 2011-2013 Pragmatic 24 Cohesion Consulting