Should a football team go for a one or two point conversion? A dynamic programming approach
- 1. Should a football team go for a one or two point conversion? A dynamic programming approach Dr. Laura Albert University of Wisconsin-Madison laura@engr.wisc.edu @lauraalbertphd (c) 2019
- 2. The problem • When an NFL team scores a touchdown, they score six points • They have two choices: – kick a point after to score 1 extra point – try for a 2 point conversion • When should they try a 2 point conversion? When should they kick an extra point? – Solution approach: dynamic programming – Model output: a series of decisions based on the score differential and the remaining time/remaining possessions (c) Laura Albert 2019 2Two point conversion DP
- 3. We make several assumptions 1. There are three possible outcomes for each team’s possession: 1. touchdown (19% of the time), 2. field goal (13% of the time), 3. no score (68% of the time). 2. The probability of success of each outcome does not depend on the score or the time left. 3. If the game ends in a tie, each team’s probability of winning is 0.5. 4. We know the number of remaining possessions. 5. The teams are equally matched Note: we can easily lift this assumption (c) Laura Albert 2019 3Two point conversion DP
- 4. Our approach • This decision depends on two factors: – The point differential – The remaining number of possessions (assumed to be known) • The state of the system depends on these two factors – The minimal amount of information needed to make our decision • The success rate for two point conversions is 48% and the success rate for extra points is 96%. (c) Laura Albert 2019 4Two point conversion DP
- 5. 5 Let’s solve this with dynamic programming (DP) • We model a sequence of interrelated decisions for two teams. • Each team seeks to maximize the probability they win the game. • DP is a general approach to problem solving, not a particular model or algorithm. • DP is smart enumeration. All possible outcomes are not enumerated, but DP guarantees the optimal solution. (c) Laura Albert 2019Two point conversion DP
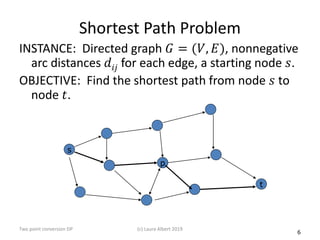
- 6. 6 Shortest Path Problem INSTANCE: Directed graph 𝐺𝐺 = (𝑉𝑉, 𝐸𝐸), nonnegative arc distances 𝑑𝑑𝑖𝑖𝑖𝑖 for each edge, a starting node 𝑠𝑠. OBJECTIVE: Find the shortest path from node 𝑠𝑠 to node 𝑡𝑡. s p t (c) Laura Albert 2019Two point conversion DP
- 7. 7 Shortest Path Problem, cont’d. • Observation 1: If the shortest path from s to r passes through node p, the subpaths (𝑠𝑠, 𝑝𝑝) and (𝑝𝑝. 𝑡𝑡) are shortest paths from 𝑠𝑠 to 𝑝𝑝 and 𝑝𝑝 to 𝑡𝑡, respectively. – If not, the shorter subpath would allow us to construct a shorter path from 𝑠𝑠 to 𝑡𝑡, leading to a contradiction. • Observation 2: Let 𝑉𝑉𝑗𝑗 denote the length of a shortest path from 𝑗𝑗 to 𝑡𝑡, then 𝑉𝑉𝑗𝑗 = min 𝑖𝑖∈𝑉𝑉𝑖𝑖{𝑗𝑗} {𝑉𝑉𝑖𝑖 + 𝑑𝑑𝑑𝑑𝑑𝑑} In other words, the lengths of the shortest paths from every neighbor of 𝑗𝑗 to 𝑡𝑡, then we can find the length of the shortest part from 𝑗𝑗 to 𝑟𝑟. Note that this is not necessarily an algorithm for finding the shortest path. (c) Laura Albert 2019Two point conversion DP
- 8. 8 Principle of Optimality • Principle of Optimality: Observations 1 and 2 define the optimal substructure of all DP models and algorithms. Each solution is characterized by – A sequence of decisions (more on this later), – The optimal solution is composed of optimal solutions to subproblems. • In the Shortest Path problem, the DP gives the shortest paths from all nodes to node 𝑡𝑡 – 𝑉𝑉𝑡𝑡 = 0. (c) Laura Albert 2019Two point conversion DP
- 9. 9 Shortest Path DP algorithms • Since DP algorithms are smart enumerations, good DP algorithms are important to find. • Let Vj n = the shortest path from j to r at iteration n. • We want to find the optimal distances Vj by initially setting Vj 0 = large number (j ≠ r) • The idea: iteratively loop over all nodes to find the best edge to traverse – Because of the principle of optimality, we only improve (lower) Vj n. (c) Laura Albert 2019Two point conversion DP
- 10. 10 Shortest Path DP algorithm 1 Bellman’s Algorithm 1. Let Vr 0=0 and Vj 0 = M, j ≠ r (M is a large number) and let n=1. 2. For all j ∈ V{r} Vj n=mini{dji+Vi n-1} 3. If Vj n < Vj n-1 for any i, let n=n+1 and return to step 2. Else stop. Note: only consider nodes where an edge from i to j exists. Problems: In step 2, most of the time we have to consider edges with distance M. A better algorithm only considers nodes with paths less than M (c) Laura Albert 2019Two point conversion DP
- 11. 11 Characteristics of DP Problems 1. Problem divided into stages with a policy decision required at each stage. Shortest path = which node to visit next 2. Each stage has a number of states associated with it. 3. The effect of each policy decision in each state (at each stage) transforms the current state into a state in the next stage (deterministic or stochastic). 4. The solution procedure is designed to find the optimal policy. Prescription for finding the best decision at each stage for each state (state-action pairs) (c) Laura Albert 2019Two point conversion DP
- 12. 12 Characteristics of DP Problems 5. Given current state, an optimal policy for the remaining stages is independent of the policy in the previous stages. This is the principle of optimality for dynamic programming 6. The solution procedure begins by finding the optimal policy for the last stage. This is usually trivial, such as 𝑉𝑉𝑡𝑡 = 0 7. A recursive relationship identifies the optimal policy for stage 𝑛𝑛, given an optimal policy for stage 𝑛𝑛 + 1 Called the value functions or optimality equations or Bellman equations or Hamilton-Jacobi-Bellman equations (c) Laura Albert 2019Two point conversion DP
- 13. Dynamic Programs as shortest or longest paths • Almost any DP problem can be formulated as a shortest or longest path (by maximizing) in a graph with directed arcs (digraph) • Nodes of the digraph correspond to states in an incomplete solution • Arcs of the digraph correspond to decisions. They link each state to a subsequent state to which the decision leads. Implication for our football problem: • The nodes represent the triplet: (1) who has the possession, (2) the current score differential, (3) how many possessions are left. • We solve a longest path problem to maximize win probability (not distance) 13 (c) Laura Albert 2019Two point conversion DP
- 14. Dynamic programming Let • 𝑉𝑉𝑛𝑛 𝐴𝐴 (𝑝𝑝) = the probability that team A wins the game if they are 𝑝𝑝 points ahead, they have just gotten the ball, and there are 𝑛𝑛 remaining possessions. • 𝑉𝑉𝑛𝑛 𝐵𝐵 (𝑝𝑝) = the probability that team A wins the game if they are 𝑝𝑝 points ahead, their opponent team B has just gotten the ball, and there are 𝑛𝑛 remaining possessions. • 𝑛𝑛 = 0 means the game is over. (c) Laura Albert 2019 14Two point conversion DP
- 15. Boundary conditions • 𝑉𝑉0 𝐴𝐴 𝑝𝑝 = 𝑉𝑉0 𝐴𝐴 𝑝𝑝 = 1 for 𝑝𝑝 > 0 • 𝑉𝑉0 𝐴𝐴 𝑝𝑝 = 𝑉𝑉0 𝐴𝐴 𝑝𝑝 = 0 for 𝑝𝑝 < 0 • 𝑉𝑉0 𝐴𝐴 𝑝𝑝 = 𝑉𝑉0 𝐴𝐴 𝑝𝑝 = 0.5 for 𝑝𝑝 = 0 [a tie] • Goal: maximizing 𝑉𝑉𝑛𝑛 𝐴𝐴(𝑝𝑝) for some 𝑛𝑛 and 𝑝𝑝 – Find by conditioning on the possession outcome and applying the law of probability (c) Laura Albert 2019 15Two point conversion DP
- 16. Law of total probability • Let 𝑋𝑋 denote a random variable. – 𝑋𝑋 is a binary variable denoting the outcome of the game (win/loss) • We can find the probability of 𝑋𝑋 given some additional information 𝑌𝑌 – 𝑌𝑌 is a random variable denoting the outcome of the current possession (touchdown, field goal, or no score). [ ] ( | ) ( ) y Y P X P X y P y ∈ = ∑ (c) Laura Albert 2019 16Two point conversion DP
- 17. Finding an expected value • Let 𝐼𝐼 be an indicator variable if the team wins: – 𝐼𝐼 = 1 if they win and 𝐼𝐼 = 0 if they lose. • The expected value of 𝐼𝐼 is the probability that the team wins 𝐸𝐸[𝐼𝐼] = 𝑃𝑃(𝐼𝐼 > 0) • 𝑃𝑃(𝐼𝐼 > 0) = 𝑉𝑉𝑛𝑛 𝐴𝐴 (𝑝𝑝) – This can be found by computing the expected value of an indicator variable 𝐸𝐸[𝐼𝐼] – This is the solution to a longest path problem! (c) Laura Albert 2019 17Two point conversion DP
- 18. Law of total probability • 𝑃𝑃𝑇𝑇𝑇𝑇 = probability of a touchdown • 𝑃𝑃𝐹𝐹𝐹𝐹 = probability of a field goal • 𝑃𝑃𝑁𝑁𝑁𝑁 = probability of no score • 𝑃𝑃𝐴𝐴𝐴𝐴 = probability of scoring a point after a touchdown • 𝑃𝑃2𝑃𝑃𝑃𝑃 = probability of a two point conversion after a touchdown Three outcomes of the current drive: TD, FG, or NS ( 𝑃𝑃𝑇𝑇𝑇𝑇 + 𝑃𝑃𝑃𝑃𝑃𝑃 + 𝑃𝑃𝑃𝑃𝑃𝑃 = 1) 𝑉𝑉𝑛𝑛+1 𝐴𝐴 𝑝𝑝 = 𝑃𝑃𝑁𝑁𝑁𝑁 𝑉𝑉𝑛𝑛 𝐵𝐵 (𝑝𝑝) No score + 𝑃𝑃𝑃𝑃𝑃𝑃 𝑉𝑉𝑛𝑛 𝐵𝐵 (𝑝𝑝 + 3) Field Goal + 𝑃𝑃𝑃𝑃𝑃𝑃 max{𝑃𝑃𝐴𝐴𝐴𝐴 𝑉𝑉𝑛𝑛 𝐵𝐵 (𝑝𝑝 + 7) + (1 − 𝑃𝑃𝐴𝐴𝐴𝐴) 𝑉𝑉𝑛𝑛 𝐵𝐵 (𝑝𝑝 + 6) , TD with AT 𝑃𝑃2𝑃𝑃𝑃𝑃 𝑉𝑉𝑛𝑛 𝐵𝐵 (𝑝𝑝 + 8) + (1 − 𝑃𝑃2𝑃𝑃𝑃𝑃) 𝑉𝑉𝑛𝑛 𝐵𝐵 (𝑝𝑝 + 6) } TD with 2PT Note: define 𝑉𝑉𝑛𝑛+1 𝐵𝐵 𝑝𝑝 in an analogous way (c) Laura Albert 2019 18Two point conversion DP
- 19. Series of equations Team A: 𝑉𝑉𝑛𝑛+1 𝐴𝐴 𝑝𝑝 = 𝑃𝑃𝑇𝑇𝑇𝑇 max{ 𝑃𝑃𝐴𝐴𝐴𝐴 𝑉𝑉𝑛𝑛 𝐵𝐵 𝑝𝑝 + 7 + 1 − 𝑃𝑃𝑃𝑃𝑃𝑃 𝑉𝑉𝑛𝑛 𝐵𝐵 𝑝𝑝 + 6 , 𝑃𝑃2𝑃𝑃𝑃𝑃 𝑉𝑉𝑛𝑛 𝐵𝐵(𝑝𝑝 + (c) Laura Albert 2019 19Two point conversion DP
- 20. Team A’s win probability Note: the points P are before the touchdown is scored V^A_n(p) Possessions remaining n P 0 1 2 3 4 5 6 7 8 9 10 -16 0 0.000 0.000 0.003 0.002 0.014 0.010 0.030 0.022 0.047 0.036 -15 0 0.000 0.000 0.006 0.004 0.020 0.014 0.038 0.029 0.058 0.044 -14 0 0.000 0.000 0.015 0.010 0.035 0.025 0.056 0.042 0.077 0.059 -13 0 0.000 0.000 0.024 0.016 0.050 0.036 0.075 0.056 0.097 0.075 -12 0 0.000 0.000 0.026 0.018 0.057 0.042 0.086 0.066 0.112 0.088 -11 0 0.000 0.000 0.035 0.026 0.074 0.056 0.108 0.084 0.136 0.108 -10 0 0.000 0.000 0.045 0.034 0.092 0.070 0.131 0.102 0.161 0.129 -9 0 0.000 0.000 0.062 0.046 0.119 0.090 0.162 0.126 0.193 0.154 -8 0 0.046 0.031 0.108 0.079 0.159 0.122 0.198 0.155 0.226 0.182 -7 0 0.091 0.062 0.154 0.113 0.199 0.153 0.234 0.186 0.260 0.212 -6 0 0.186 0.127 0.252 0.183 0.283 0.216 0.303 0.240 0.318 0.258 -5 0 0.190 0.135 0.271 0.202 0.311 0.242 0.334 0.268 0.350 0.288 -4 0 0.190 0.141 0.282 0.218 0.332 0.265 0.362 0.296 0.382 0.319 -3 0 0.255 0.198 0.362 0.288 0.409 0.332 0.430 0.356 0.441 0.371 -2 0 0.320 0.243 0.427 0.336 0.465 0.378 0.480 0.398 0.485 0.410 -1 0 0.320 0.251 0.440 0.357 0.489 0.405 0.509 0.430 0.518 0.444 0 0.5 0.660 0.500 0.622 0.500 0.601 0.500 0.588 0.500 0.579 0.500 1 1 1.000 0.749 0.805 0.643 0.714 0.594 0.667 0.569 0.639 0.555 2 1 1.000 0.757 0.817 0.662 0.736 0.621 0.695 0.600 0.670 0.588 3 1 1.000 0.803 0.849 0.713 0.774 0.668 0.733 0.644 0.708 0.628 4 1 1.000 0.859 0.896 0.782 0.832 0.734 0.789 0.703 0.758 0.681 Team A’s last possession Team A’s second to last possession(c) Laura Albert 2019 20Two point conversion DP Boundary conditions
- 21. How do we determine whether to go for two points? Test the condition in the max statement to see what was selected: For Team A who gets the ball with 𝑛𝑛 + 1 possessions to go and is up by 𝑝𝑝 points 𝑉𝑉𝑛𝑛+1 𝐴𝐴 𝑝𝑝 𝑃𝑃𝐴𝐴𝐴𝐴 𝑉𝑉𝑛𝑛 𝐵𝐵 𝑝𝑝 + 7 + 1 − 𝑃𝑃𝑃𝑃𝑃𝑃 𝑉𝑉𝑛𝑛 𝐵𝐵 𝑝𝑝 + 6 < 𝑃𝑃2𝑃𝑃𝑃𝑃 𝑉𝑉𝑛𝑛 𝐵𝐵 𝑝𝑝 + 8 + 1 − 𝑃𝑃2𝑃𝑃𝑃𝑃 𝑉𝑉𝑛𝑛 𝐵𝐵 𝑝𝑝 + 6 Then go for two points is better than going for one point. A similar approach works for Team B by solving 𝑉𝑉𝑛𝑛+1 𝐵𝐵 𝑝𝑝 (c) Laura Albert 2019 21Two point conversion DP
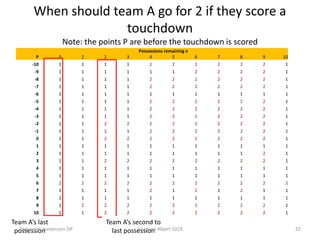
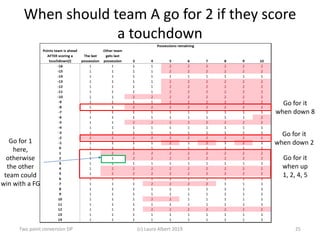
- 22. When should team A go for 2 if they score a touchdown Note: the points P are before the touchdown is scored Possessions remaining n P 0 2 2 3 4 5 6 7 8 9 10 -10 1 1 1 1 2 2 2 2 2 2 1 -9 1 1 1 1 1 1 2 2 2 2 1 -8 1 1 1 1 2 2 2 2 2 2 1 -7 1 1 1 1 2 2 2 2 2 2 1 -6 1 1 1 1 1 1 1 1 1 1 1 -5 1 1 1 1 2 2 2 2 2 2 1 -4 1 1 1 1 2 2 2 2 2 2 1 -3 1 1 1 1 2 2 2 2 2 2 1 -2 1 1 2 2 2 2 2 2 2 2 1 -1 1 1 1 1 2 2 2 2 2 2 1 0 1 1 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 2 1 3 1 1 2 2 2 2 2 2 2 2 1 4 1 1 1 1 1 1 1 1 1 1 1 5 1 1 1 1 1 1 1 1 1 1 1 6 2 2 2 2 2 2 2 2 2 2 2 7 1 1 1 1 2 1 2 1 2 1 1 8 1 1 1 1 1 1 1 1 1 1 1 9 1 2 2 2 2 2 2 2 2 2 1 10 1 1 2 2 2 2 2 2 2 2 1 Team A’s last possession Team A’s second to last possession(c) Laura Albert 2019 22Two point conversion DP
- 23. When should team A go for 2 if they score a touchdown Two point conversion DP (c) Laura Albert 2019 23 Team A’s last possession Team A’s second to last possession
- 24. When should Team A go for 2? On their last possession (from 𝑉𝑉1 𝐴𝐴 𝑝𝑝 ): When 𝑝𝑝 = −8 i.e., when Team A is down 8 and then scores a touchdown Team A would be tied or down 2 after this possession. On their second to last possession (from 𝑉𝑉3 𝐴𝐴 𝑝𝑝 ): When 𝑝𝑝 = −16, −14, −11, −8, −5, −4, −2, −1 (Or 𝑝𝑝 = −10, −8, −3, −2, 1, 2, 4, 5 including the 6 points from the touchdown) Note: the points 𝑝𝑝 are before the touchdown is scored (c) Laura Albert 2019 24Two point conversion DP
- 25. When should team A go for 2 if they score a touchdown Two point conversion DP (c) Laura Albert 2019 25 Go for it when down 2 Go for it when down 8 Go for it when up 1, 2, 4, 5 Go for 1 here, otherwise the other team could win with a FG
- 26. When should Team A go for 2? When we set 𝑃𝑃𝐴𝐴𝐴𝐴 = 0.95 (from 0.96) the results change slightly: • Team A should go for 2 if they score a touchdown when down 15 before the touchdown • Note: the win probability does not change very much On their second to last possession (from 𝑉𝑉3 𝐴𝐴 𝑝𝑝 ): When 𝑝𝑝 = −16, −𝟏𝟏𝟏𝟏, −14, −11, −8, −5, −4, −2, −1 Note: the points 𝑝𝑝 are before the touchdown is scored How much does going for 2 improve the win probability? (c) Laura Albert 2019 26Two point conversion DP
- 27. How much does going for 2 improve the win probability? Answer: not by much. Rationale: if you are down by 15, you have to score two touchdowns while keeping your opponent from scoring. • If down by 8 (before the 6 TD points) with 1 or 3 possessions to go, the strategy improves the win probability by 4.6% or 4.5%. • If down by 1, 5, or 11 (before the 6 TD points), the strategy improves the win probability by 0.6 – 1.8% depending on the remaining number of possessions • If down by 14, 15, or 16 (before the 6 TD points), the strategy improves the win probability by <1% In some scenarios, the win probability gets worse (!) • Your opponent is also finding the best strategy The win probability can be further improved by improving other decisions • E.g., Going for it on fourth down, better play calling Two point conversion DP (c) Laura Albert 2019 27
- 28. Why would a team go for 2 when they are down by 8? Let’s say a team is down by 14 and scores a touchdown, putting them down by 8. Let’s say there will be 4 possessions left after this possession. • Traditional decision: go for 1 point. If they succeed (with probability 0.96), they will have a 11.3% probability of winning. If they do not succeed, they will have a 7.9% probability of winning Overall: 11.2% win probability • Going for a two point conversion If they succeed (with probability 0.48), they will have a 18.3% probability of winning. If they do not succeed, they will have a 7.9% probability of winning Overall: 12.9% win probability Two point conversion DP (c) Laura Albert 2019 28














![Boundary conditions
• 𝑉𝑉0
𝐴𝐴
𝑝𝑝 = 𝑉𝑉0
𝐴𝐴
𝑝𝑝 = 1 for 𝑝𝑝 > 0
• 𝑉𝑉0
𝐴𝐴
𝑝𝑝 = 𝑉𝑉0
𝐴𝐴
𝑝𝑝 = 0 for 𝑝𝑝 < 0
• 𝑉𝑉0
𝐴𝐴
𝑝𝑝 = 𝑉𝑉0
𝐴𝐴
𝑝𝑝 = 0.5 for 𝑝𝑝 = 0 [a tie]
• Goal: maximizing 𝑉𝑉𝑛𝑛
𝐴𝐴(𝑝𝑝) for some 𝑛𝑛 and 𝑝𝑝
– Find by conditioning on the possession outcome and
applying the law of probability
(c) Laura Albert 2019 15Two point conversion DP](https://image.slidesharecdn.com/dynamicprogrammingtwopointconversiondynamicprogramming2019-191118191310/85/Should-a-football-team-go-for-a-one-or-two-point-conversion-A-dynamic-programming-approach-15-320.jpg)
![Law of total probability
• Let 𝑋𝑋 denote a random variable.
– 𝑋𝑋 is a binary variable denoting the outcome of the game
(win/loss)
• We can find the probability of 𝑋𝑋 given some
additional information 𝑌𝑌
– 𝑌𝑌 is a random variable denoting the outcome of the
current possession (touchdown, field goal, or no score).
[ ] ( | ) ( )
y Y
P X P X y P y
∈
= ∑
(c) Laura Albert 2019 16Two point conversion DP](https://image.slidesharecdn.com/dynamicprogrammingtwopointconversiondynamicprogramming2019-191118191310/85/Should-a-football-team-go-for-a-one-or-two-point-conversion-A-dynamic-programming-approach-16-320.jpg)
![Finding an expected value
• Let 𝐼𝐼 be an indicator variable if the team wins:
– 𝐼𝐼 = 1 if they win and 𝐼𝐼 = 0 if they lose.
• The expected value of 𝐼𝐼 is the probability that the team wins
𝐸𝐸[𝐼𝐼] = 𝑃𝑃(𝐼𝐼 > 0)
• 𝑃𝑃(𝐼𝐼 > 0) = 𝑉𝑉𝑛𝑛
𝐴𝐴
(𝑝𝑝)
– This can be found by computing the expected value of an
indicator variable 𝐸𝐸[𝐼𝐼]
– This is the solution to a longest path problem!
(c) Laura Albert 2019 17Two point conversion DP](https://image.slidesharecdn.com/dynamicprogrammingtwopointconversiondynamicprogramming2019-191118191310/85/Should-a-football-team-go-for-a-one-or-two-point-conversion-A-dynamic-programming-approach-17-320.jpg)