20110409 quantum algorithms_vyali_lecture06
- 1. Квантовые алгоритмы: возможности и ограничения. Лекция 6: Квантовые схемы М. Вялый Вычислительный центр им. А.А.Дородницына Российской Академии наук Санкт-Петербург, 2011 М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 1 / 36
- 2. План 1 Трудоемкость квантового вычисления 2 Точная реализация унитарных операторов квантовыми схемами Обратимые вычисления: мостик между классическими и квантовыми Базис из операторов, действующих на одном кубите Базис из операторов, действующих на двух кубитах 3 Об унитарных преобразованиях одного кубита М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 2 / 36
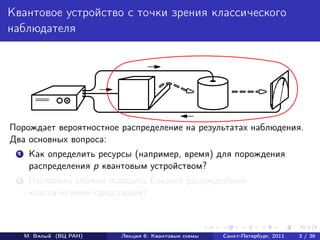
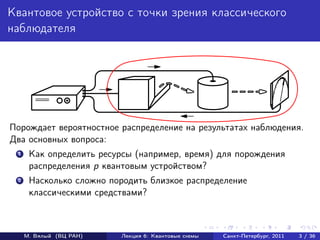
- 3. Квантовое устройство с точки зрения классического наблюдателя Порождает вероятностное распределение на результатах наблюдения. Два основных вопроса: 1 Как определить ресурсы (например, время) для порождения распределения p квантовым устройством? 2 Насколько сложно породить близкое распределение классическими средствами? М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 3 / 36
- 4. Квантовое устройство с точки зрения классического наблюдателя Порождает вероятностное распределение на результатах наблюдения. Два основных вопроса: 1 Как определить ресурсы (например, время) для порождения распределения p квантовым устройством? 2 Насколько сложно породить близкое распределение классическими средствами? М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 3 / 36
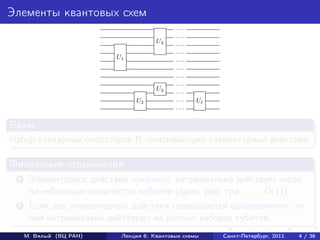
- 5. Элементы квантовых схем ... ... U4 ... ... U1 ... ... ... ... U3 ... U2 ... U ... Базис Набор унитарных операторов B, описывающих элементарные действия. Физические ограничения 1 Элементарное действие локально: нетривиально действует лишь на небольшое количество кубитов (один, два, три, . . . , O(1)). 2 Если два элементарных действия совершаются одновременно, то они нетривиально действуют на разных наборах кубитов. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 4 / 36
- 6. Элементы квантовых схем ... ... U4 ... ... U1 ... ... ... ... U3 ... U2 ... U ... Базис Набор унитарных операторов B, описывающих элементарные действия. Физические ограничения 1 Элементарное действие локально: нетривиально действует лишь на небольшое количество кубитов (один, два, три, . . . , O(1)). 2 Если два элементарных действия совершаются одновременно, то они нетривиально действуют на разных наборах кубитов. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 4 / 36
- 7. Элементы квантовых схем ... ... U4 ... ... U1 ... ... ... ... U3 ... U2 ... U ... Базис Набор унитарных операторов B, описывающих элементарные действия. Физические ограничения 1 Элементарное действие локально: нетривиально действует лишь на небольшое количество кубитов (один, два, три, . . . , O(1)). 2 Если два элементарных действия совершаются одновременно, то они нетривиально действуют на разных наборах кубитов. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 4 / 36
- 8. Квантовая схема над базисом B: определение ... ... U4 ... ... U1 ... ... ... ... U3 ... U2 ... U ... Квантовая схема Последовательность операторов U1 [S1 ], U2 [S2 ], . . . , U [S ], где Uk ∈ B, Sk ⊆ {1, . . . , n}, n количество используемых кубитов. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 5 / 36
- 9. Матричные элементы U[S] Пусть U= ux,y |x y |, x,y ∈{0,1}d S = {j1 , . . . , jd }. Обозначим x[S] подпоследовательность битов, стоящих на местах из множества S. Тогда U[S] = ux[S],y [S] |x y |. ¯ ¯ x,y ∈{0,1}n :x[S]=y [S] М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 6 / 36
- 10. Матричные элементы U[S] Пусть U= ux,y |x y |, x,y ∈{0,1}d S = {j1 , . . . , jd }. Обозначим x[S] подпоследовательность битов, стоящих на местах из множества S. Тогда U[S] = ux[S],y [S] |x y |. ¯ ¯ x,y ∈{0,1}n :x[S]=y [S] М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 6 / 36
- 11. Матричные элементы U[S] Пусть U= ux,y |x y |, x,y ∈{0,1}d S = {j1 , . . . , jd }. Обозначим x[S] подпоследовательность битов, стоящих на местах из множества S. Тогда U[S] = ux[S],y [S] |x y |. ¯ ¯ x,y ∈{0,1}n :x[S]=y [S] М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 6 / 36
- 12. Меры сложности схемы Размер схемы Количество элементов в схеме. Отвечает за время вычисления на последовательном устройстве. Глубина схемы Наименьшее количество слоев, в которые можно расположить элементы схемы при соблюдении условий: 1 элементы, которые стоят в схеме после j-го, не попадают в слои, предшествующие слою, в котором находится j-й элемент; 2 элементы из одного слоя действуют на непересекающиеся множества кубитов. Глубина отвечает за время вычисления на параллельном устройстве. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 7 / 36
- 13. Меры сложности схемы Размер схемы Количество элементов в схеме. Отвечает за время вычисления на последовательном устройстве. Глубина схемы Наименьшее количество слоев, в которые можно расположить элементы схемы при соблюдении условий: 1 элементы, которые стоят в схеме после j-го, не попадают в слои, предшествующие слою, в котором находится j-й элемент; 2 элементы из одного слоя действуют на непересекающиеся множества кубитов. Глубина отвечает за время вычисления на параллельном устройстве. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 7 / 36
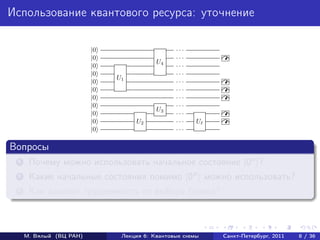
- 14. Использование квантового ресурса: уточнение |0 ... |0 ... U4 ... |0 |0 ... U1 ... |0 |0 ... |0 ... |0 ... U3 ... |0 |0 U2 ... U |0 ... Вопросы 1 Почему можно использовать начальное состояние |0n ? 2 Какие начальные состояния помимо |0n можно использовать? 3 Как зависит трудоемкость от выбора базиса? М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 8 / 36
- 15. Использование квантового ресурса: уточнение |0 ... |0 ... U4 ... |0 |0 ... U1 ... |0 |0 ... |0 ... |0 ... U3 ... |0 |0 U2 ... U |0 ... Вопросы 1 Почему можно использовать начальное состояние |0n ? 2 Какие начальные состояния помимо |0n можно использовать? 3 Как зависит трудоемкость от выбора базиса? М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 8 / 36
- 16. Использование квантового ресурса: уточнение |0 ... |0 ... U4 ... |0 |0 ... U1 ... |0 |0 ... |0 ... |0 ... U3 ... |0 |0 U2 ... U |0 ... Вопросы 1 Почему можно использовать начальное состояние |0n ? 2 Какие начальные состояния помимо |0n можно использовать? 3 Как зависит трудоемкость от выбора базиса? М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 8 / 36
- 17. Использование квантового ресурса: уточнение |0 ... |0 ... U4 ... |0 |0 ... U1 ... |0 |0 ... |0 ... |0 ... U3 ... |0 |0 U2 ... U |0 ... Вопросы 1 Почему можно использовать начальное состояние |0n ? 2 Какие начальные состояния помимо |0n можно использовать? 3 Как зависит трудоемкость от выбора базиса? М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 8 / 36
- 18. Использование квантового ресурса: уточнение |0 ... |0 ... U4 ... |0 |0 ... U1 ... |0 |0 ... |0 ... |0 ... U3 ... |0 |0 U2 ... U |0 ... Вопросы 1 Почему можно использовать начальное состояние |0n ? 2 Какие начальные состояния помимо |0n можно использовать? 3 Как зависит трудоемкость от выбора базиса? М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 8 / 36
- 19. Ответ на первый вопрос Утверждение Если есть прибор, измеряющий в вычислительном базисе, то можно приготавливать состояния из вычислительного базиса. Порядок действий при изготовлении состояния |0 : 1 Берем случайное состояние. 2 Измеряем его в вычислительном базисе. 3 Если наблюдаем исход 0, то кубит находится в состоянии |0 : готово. 4 В противном случае повторяем процедуру. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 9 / 36
- 20. Ответ на первый вопрос Утверждение Если есть прибор, измеряющий в вычислительном базисе, то можно приготавливать состояния из вычислительного базиса. Порядок действий при изготовлении состояния |0 : 1 Берем случайное состояние. 2 Измеряем его в вычислительном базисе. 3 Если наблюдаем исход 0, то кубит находится в состоянии |0 : готово. 4 В противном случае повторяем процедуру. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 9 / 36
- 21. Ответ на первый вопрос Утверждение Если есть прибор, измеряющий в вычислительном базисе, то можно приготавливать состояния из вычислительного базиса. Порядок действий при изготовлении состояния |0 : 1 Берем случайное состояние. 2 Измеряем его в вычислительном базисе. 3 Если наблюдаем исход 0, то кубит находится в состоянии |0 : готово. 4 В противном случае повторяем процедуру. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 9 / 36
- 22. Ответ на первый вопрос Утверждение Если есть прибор, измеряющий в вычислительном базисе, то можно приготавливать состояния из вычислительного базиса. Порядок действий при изготовлении состояния |0 : 1 Берем случайное состояние. 2 Измеряем его в вычислительном базисе. 3 Если наблюдаем исход 0, то кубит находится в состоянии |0 : готово. 4 В противном случае повторяем процедуру. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 9 / 36
- 23. Ответ на первый вопрос Утверждение Если есть прибор, измеряющий в вычислительном базисе, то можно приготавливать состояния из вычислительного базиса. Порядок действий при изготовлении состояния |0 : 1 Берем случайное состояние. 2 Измеряем его в вычислительном базисе. 3 Если наблюдаем исход 0, то кубит находится в состоянии |0 : готово. 4 В противном случае повторяем процедуру. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 9 / 36
- 24. Ответ на первый вопрос Утверждение Если есть прибор, измеряющий в вычислительном базисе, то можно приготавливать состояния из вычислительного базиса. Порядок действий при изготовлении состояния |0 : 1 Берем случайное состояние. 2 Измеряем его в вычислительном базисе. 3 Если наблюдаем исход 0, то кубит находится в состоянии |0 : готово. 4 В противном случае повторяем процедуру. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 9 / 36
- 25. Ответ на второй вопрос Зависит от законов физики. Но вряд ли есть еще какие-нибудь интересные варианты. Ясно, что начальное состояние нужно уметь приготавливать достаточно быстро. Годятся любые состояния из вычислительного базиса А также те, которые получаются из них действием достаточно коротких схем. Но это неинтересно, поскольку схему приготовления состояния можно включить в основную схему. Есть ли в природе другие возможности? М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 10 / 36
- 26. Ответ на второй вопрос Зависит от законов физики. Но вряд ли есть еще какие-нибудь интересные варианты. Ясно, что начальное состояние нужно уметь приготавливать достаточно быстро. Годятся любые состояния из вычислительного базиса А также те, которые получаются из них действием достаточно коротких схем. Но это неинтересно, поскольку схему приготовления состояния можно включить в основную схему. Есть ли в природе другие возможности? М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 10 / 36
- 27. Ответ на второй вопрос Зависит от законов физики. Но вряд ли есть еще какие-нибудь интересные варианты. Ясно, что начальное состояние нужно уметь приготавливать достаточно быстро. Годятся любые состояния из вычислительного базиса А также те, которые получаются из них действием достаточно коротких схем. Но это неинтересно, поскольку схему приготовления состояния можно включить в основную схему. Есть ли в природе другие возможности? М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 10 / 36
- 28. Ответ на второй вопрос Зависит от законов физики. Но вряд ли есть еще какие-нибудь интересные варианты. Ясно, что начальное состояние нужно уметь приготавливать достаточно быстро. Годятся любые состояния из вычислительного базиса А также те, которые получаются из них действием достаточно коротких схем. Но это неинтересно, поскольку схему приготовления состояния можно включить в основную схему. Есть ли в природе другие возможности? М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 10 / 36
- 29. Ответ на второй вопрос Зависит от законов физики. Но вряд ли есть еще какие-нибудь интересные варианты. Ясно, что начальное состояние нужно уметь приготавливать достаточно быстро. Годятся любые состояния из вычислительного базиса А также те, которые получаются из них действием достаточно коротких схем. Но это неинтересно, поскольку схему приготовления состояния можно включить в основную схему. Есть ли в природе другие возможности? М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 10 / 36
- 30. Ответ на второй вопрос Зависит от законов физики. Но вряд ли есть еще какие-нибудь интересные варианты. Ясно, что начальное состояние нужно уметь приготавливать достаточно быстро. Годятся любые состояния из вычислительного базиса А также те, которые получаются из них действием достаточно коротких схем. Но это неинтересно, поскольку схему приготовления состояния можно включить в основную схему. Есть ли в природе другие возможности? М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 10 / 36
- 31. Ответы на третий вопрос Базис из операторов, действующих на одном кубите, неинтересен (моделируется классически). Базисы из операторов, действующих на k кубитах, эффективно эквивалентны для всех k. Более того, существует конечный базис из операторов, действующих не более чем на двух кубитах, который им всем эффективно эквивалентен (при разумных предположениях). М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 11 / 36
- 32. Ответы на третий вопрос Базис из операторов, действующих на одном кубите, неинтересен (моделируется классически). Базисы из операторов, действующих на k кубитах, эффективно эквивалентны для всех k. Более того, существует конечный базис из операторов, действующих не более чем на двух кубитах, который им всем эффективно эквивалентен (при разумных предположениях). М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 11 / 36
- 33. Ответы на третий вопрос Базис из операторов, действующих на одном кубите, неинтересен (моделируется классически). Базисы из операторов, действующих на k кубитах, эффективно эквивалентны для всех k. Более того, существует конечный базис из операторов, действующих не более чем на двух кубитах, который им всем эффективно эквивалентен (при разумных предположениях). М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 11 / 36
- 34. План 1 Трудоемкость квантового вычисления 2 Точная реализация унитарных операторов квантовыми схемами Обратимые вычисления: мостик между классическими и квантовыми Базис из операторов, действующих на одном кубите Базис из операторов, действующих на двух кубитах 3 Об унитарных преобразованиях одного кубита М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 12 / 36
- 35. Определения Схема U1 [S1 ], U2 [S2 ], . . . , U [S ] реализует оператор U = U [S ] . . . U2 [S2 ]U1 [S1 ] (обратите внимание на порядок). Схема U1 [S1 ], U2 [S2 ], . . . , U [S ] реализует оператор U в расширенном смысле, если U [S ] . . . U2 [S2 ]U1 [S1 ] : |ψ ⊗ |0N → U|ψ ⊗ |0N для всех |ψ ∈ (C2 )⊗n . Сложностью реализации оператора U (в расширенном смысле) в базисе B называется наименьший размер схемы в базисе B, реализующей U (в расширенном смысле). Сложность бесконечна, если реализации не существует. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 13 / 36
- 36. Определения Схема U1 [S1 ], U2 [S2 ], . . . , U [S ] реализует оператор U = U [S ] . . . U2 [S2 ]U1 [S1 ] (обратите внимание на порядок). Схема U1 [S1 ], U2 [S2 ], . . . , U [S ] реализует оператор U в расширенном смысле, если U [S ] . . . U2 [S2 ]U1 [S1 ] : |ψ ⊗ |0N → U|ψ ⊗ |0N для всех |ψ ∈ (C2 )⊗n . Сложностью реализации оператора U (в расширенном смысле) в базисе B называется наименьший размер схемы в базисе B, реализующей U (в расширенном смысле). Сложность бесконечна, если реализации не существует. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 13 / 36
- 37. Определения Схема U1 [S1 ], U2 [S2 ], . . . , U [S ] реализует оператор U = U [S ] . . . U2 [S2 ]U1 [S1 ] (обратите внимание на порядок). Схема U1 [S1 ], U2 [S2 ], . . . , U [S ] реализует оператор U в расширенном смысле, если U [S ] . . . U2 [S2 ]U1 [S1 ] : |ψ ⊗ |0N → U|ψ ⊗ |0N для всех |ψ ∈ (C2 )⊗n . Сложностью реализации оператора U (в расширенном смысле) в базисе B называется наименьший размер схемы в базисе B, реализующей U (в расширенном смысле). Сложность бесконечна, если реализации не существует. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 13 / 36
- 38. О реализации в расширенном смысле Основная цель моделировать вероятностные распределения, порождаемые унитарными операторами. Условие реализации в расширенном смысле гарантирует, что при измерении состояния U [S ] . . . U2 [S2 ]U1 [S1 ](|ψ ⊗ |0N ) значения кубитов первого регистра распределены также, как при измерении состояния U|ψ . Достаточны и более слабые условия, например, U [S ] . . . U2 [S2 ]U1 [S1 ] : |ψ ⊗ |0N → U|ψ ⊗ V |ψ . (∗) Однако, это условие не слишком добавляет общности. Задача Докажите, что из выполнения (∗) следует V |ψ = |ξ для любого ψ. Дополнительным преимуществом условия реализации в расширенном смысле является сохранение этого свойства при композициях. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 14 / 36
- 39. Перестановочные операторы Определение Унитарный оператор назовем перестановочным, если он сохраняет множество базисных векторов. Перестановочный оператор действует классически. Если ограничить базис только перестановочными операторами, то предыдущие определения дают понятие обратимого вычисления. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 15 / 36
- 40. Перестановочные операторы Определение Унитарный оператор назовем перестановочным, если он сохраняет множество базисных векторов. Перестановочный оператор действует классически. Если ограничить базис только перестановочными операторами, то предыдущие определения дают понятие обратимого вычисления. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 15 / 36
- 41. Необратимое вычисление: моделирование обратимым Если разрешить вместо перестановок базисных векторов любые отображения, получим обычные классические схемы. Базис из отображений на двух битах полный (проверьте, что достаточно использовать в базисе булевы функции от двух переменных). По классическому базису B = {f1 , . . . , fm } из функций fk : {0, 1}dk → {0, 1} построим обратимый базис B⊕ = {fk⊕ , c-NOT}, где fk⊕ : (x, y ) → (x, y ⊕ fk (x)), c-NOT : (x, y ) → (x, x ⊕ y ). Теорема (реализация в расширенном смысле) Если отображение F : {0, 1}n → {0, 1}m реализуется булевой схемой размера L в базисе B, то существует схема размера O(L + m) в базисе B⊕ , которая реализует отображение F ⊕ : (x, y , 0L ) → (x, y ⊕ F (x), 0L ). М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 16 / 36
- 42. Необратимое вычисление: моделирование обратимым Если разрешить вместо перестановок базисных векторов любые отображения, получим обычные классические схемы. Базис из отображений на двух битах полный (проверьте, что достаточно использовать в базисе булевы функции от двух переменных). По классическому базису B = {f1 , . . . , fm } из функций fk : {0, 1}dk → {0, 1} построим обратимый базис B⊕ = {fk⊕ , c-NOT}, где fk⊕ : (x, y ) → (x, y ⊕ fk (x)), c-NOT : (x, y ) → (x, x ⊕ y ). Теорема (реализация в расширенном смысле) Если отображение F : {0, 1}n → {0, 1}m реализуется булевой схемой размера L в базисе B, то существует схема размера O(L + m) в базисе B⊕ , которая реализует отображение F ⊕ : (x, y , 0L ) → (x, y ⊕ F (x), 0L ). М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 16 / 36
- 43. Необратимое вычисление: моделирование обратимым Если разрешить вместо перестановок базисных векторов любые отображения, получим обычные классические схемы. Базис из отображений на двух битах полный (проверьте, что достаточно использовать в базисе булевы функции от двух переменных). По классическому базису B = {f1 , . . . , fm } из функций fk : {0, 1}dk → {0, 1} построим обратимый базис B⊕ = {fk⊕ , c-NOT}, где fk⊕ : (x, y ) → (x, y ⊕ fk (x)), c-NOT : (x, y ) → (x, x ⊕ y ). Теорема (реализация в расширенном смысле) Если отображение F : {0, 1}n → {0, 1}m реализуется булевой схемой размера L в базисе B, то существует схема размера O(L + m) в базисе B⊕ , которая реализует отображение F ⊕ : (x, y , 0L ) → (x, y ⊕ F (x), 0L ). М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 16 / 36
- 44. Необратимое вычисление: моделирование обратимым Если разрешить вместо перестановок базисных векторов любые отображения, получим обычные классические схемы. Базис из отображений на двух битах полный (проверьте, что достаточно использовать в базисе булевы функции от двух переменных). По классическому базису B = {f1 , . . . , fm } из функций fk : {0, 1}dk → {0, 1} построим обратимый базис B⊕ = {fk⊕ , c-NOT}, где fk⊕ : (x, y ) → (x, y ⊕ fk (x)), c-NOT : (x, y ) → (x, x ⊕ y ). Теорема (реализация в расширенном смысле) Если отображение F : {0, 1}n → {0, 1}m реализуется булевой схемой размера L в базисе B, то существует схема размера O(L + m) в базисе B⊕ , которая реализует отображение F ⊕ : (x, y , 0L ) → (x, y ⊕ F (x), 0L ). М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 16 / 36
- 45. Набросок доказательства Представим схему как последовательность присваиваний zj := fkj (предыдущие значения и входные переменные). Сопоставим битам из третьего регистра вспомогательные переменные схемы zj (результаты присваиваний). Заменим каждое присваивание на применение соответствующего fk⊕ к соответствующим битам. Получим состояние j x y z1 z2 . . . zL Скопируем, используя c-NOT, биты ответа во второй регистр. Откатим все шаги, кроме последнего (в порядке, обратном первоначальному). М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 17 / 36
- 46. Набросок доказательства Представим схему как последовательность присваиваний zj := fkj (предыдущие значения и входные переменные). Сопоставим битам из третьего регистра вспомогательные переменные схемы zj (результаты присваиваний). Заменим каждое присваивание на применение соответствующего fk⊕ к соответствующим битам. Получим состояние j x y z1 z2 . . . zL Скопируем, используя c-NOT, биты ответа во второй регистр. Откатим все шаги, кроме последнего (в порядке, обратном первоначальному). М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 17 / 36
- 47. Набросок доказательства Представим схему как последовательность присваиваний zj := fkj (предыдущие значения и входные переменные). Сопоставим битам из третьего регистра вспомогательные переменные схемы zj (результаты присваиваний). Заменим каждое присваивание на применение соответствующего fk⊕ к соответствующим битам. Получим состояние j x y z1 z2 . . . zL Скопируем, используя c-NOT, биты ответа во второй регистр. Откатим все шаги, кроме последнего (в порядке, обратном первоначальному). М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 17 / 36
- 48. Набросок доказательства Представим схему как последовательность присваиваний zj := fkj (предыдущие значения и входные переменные). Сопоставим битам из третьего регистра вспомогательные переменные схемы zj (результаты присваиваний). Заменим каждое присваивание на применение соответствующего fk⊕ к соответствующим битам. Получим состояние j x y z1 z2 . . . zL Скопируем, используя c-NOT, биты ответа во второй регистр. Откатим все шаги, кроме последнего (в порядке, обратном первоначальному). М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 17 / 36
- 49. Набросок доказательства Представим схему как последовательность присваиваний zj := fkj (предыдущие значения и входные переменные). Сопоставим битам из третьего регистра вспомогательные переменные схемы zj (результаты присваиваний). Заменим каждое присваивание на применение соответствующего fk⊕ к соответствующим битам. Получим состояние j x y z1 z2 . . . zL Скопируем, используя c-NOT, биты ответа во второй регистр. Откатим все шаги, кроме последнего (в порядке, обратном первоначальному). М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 17 / 36
- 50. Откатка (uncompute) В общем случае для откатки нужно применять обратные операторы. Но f ⊕ инволютивна: f⊕ f⊕ (x, y ) −→ (x, y ⊕ f (x)) −→ (x, y ⊕ f (x) ⊕ f (x)) = (x, y ) − − М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 18 / 36
- 51. Комментарии Теорема Любая булева функция реализуется схемами в базисе (конъюнкция, отрицание). Следствие (NOT-базис) Любое отображение F : {0, 1}n → {0, 1}m реализуется в расширенном смысле (с использованием вспомогательных битов, не меняющих своего значения после вычисления) в базисе σx = NOT : x → 1 ⊕ x; c-NOT : (x, y ) → (x, x ⊕ y ); cc-NOT : (x, y , z) → (x, y , z ⊕ xy ) (элемент Тоффоли). Задача Докажите, что в базисе из перестановок двух битов не все отображения реализуемы в расширенном смысле. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 19 / 36
- 52. Комментарии Теорема Любая булева функция реализуется схемами в базисе (конъюнкция, отрицание). Следствие (NOT-базис) Любое отображение F : {0, 1}n → {0, 1}m реализуется в расширенном смысле (с использованием вспомогательных битов, не меняющих своего значения после вычисления) в базисе σx = NOT : x → 1 ⊕ x; c-NOT : (x, y ) → (x, x ⊕ y ); cc-NOT : (x, y , z) → (x, y , z ⊕ xy ) (элемент Тоффоли). Задача Докажите, что в базисе из перестановок двух битов не все отображения реализуемы в расширенном смысле. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 19 / 36
- 53. Комментарии Теорема Любая булева функция реализуется схемами в базисе (конъюнкция, отрицание). Следствие (NOT-базис) Любое отображение F : {0, 1}n → {0, 1}m реализуется в расширенном смысле (с использованием вспомогательных битов, не меняющих своего значения после вычисления) в базисе σx = NOT : x → 1 ⊕ x; c-NOT : (x, y ) → (x, x ⊕ y ); cc-NOT : (x, y , z) → (x, y , z ⊕ xy ) (элемент Тоффоли). Задача Докажите, что в базисе из перестановок двух битов не все отображения реализуемы в расширенном смысле. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 19 / 36
- 54. Комментарии (продолжение) Задача Докажите, что без использования вспомогательных битов невозможно реализовать отображение c(n) -NOT : (x1 , . . . , xn , y ) → (x1 , . . . , xn , y ⊕ x1 x2 . . . xn ) в базисе из перестановок n битов. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 20 / 36
- 55. Базис из операторов, действующих на одном кубите (U1 ⊗ I )(I ⊗ U2 ) = U1 ⊗ U2 = (I ⊗ U2 )(U1 ⊗ I ) Поэтому в таком базисе реализуются лишь операторы вида U1 ⊗ U2 ⊗ · · · ⊗ Un , а исходы при наблюдении распределены независимо для каждого кубита. Такое распределение моделируется классически. Но! М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 21 / 36
- 56. Базис из операторов, действующих на одном кубите (U1 ⊗ I )(I ⊗ U2 ) = U1 ⊗ U2 = (I ⊗ U2 )(U1 ⊗ I ) Поэтому в таком базисе реализуются лишь операторы вида U1 ⊗ U2 ⊗ · · · ⊗ Un , а исходы при наблюдении распределены независимо для каждого кубита. Такое распределение моделируется классически. Но! М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 21 / 36
- 57. Базис из операторов, действующих на одном кубите (U1 ⊗ I )(I ⊗ U2 ) = U1 ⊗ U2 = (I ⊗ U2 )(U1 ⊗ I ) Поэтому в таком базисе реализуются лишь операторы вида U1 ⊗ U2 ⊗ · · · ⊗ Un , а исходы при наблюдении распределены независимо для каждого кубита. Такое распределение моделируется классически. Но! Использование произвольных распределений на {0, 1} делает некоторые невычислимые функции вычислимыми (пусть биты p(1) вероятности 1 образуют невычислимую последователь- ность). Трудность общая для вероятностных и квантовых вычислений. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 21 / 36
- 58. Базис из операторов, действующих на одном кубите (U1 ⊗ I )(I ⊗ U2 ) = U1 ⊗ U2 = (I ⊗ U2 )(U1 ⊗ I ) Поэтому в таком базисе реализуются лишь операторы вида U1 ⊗ U2 ⊗ · · · ⊗ Un , а исходы при наблюдении распределены независимо для каждого кубита. Такое распределение моделируется классически. Но! В случае вероятностных вычислений стандартный выход состо- ит в использовании равномерного распределения на некотором числе кубитов. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 21 / 36
- 59. Базис из операторов, действующих на одном кубите (U1 ⊗ I )(I ⊗ U2 ) = U1 ⊗ U2 = (I ⊗ U2 )(U1 ⊗ I ) Поэтому в таком базисе реализуются лишь операторы вида U1 ⊗ U2 ⊗ · · · ⊗ Un , а исходы при наблюдении распределены независимо для каждого кубита. Такое распределение моделируется классически. Но! В квантовом случае трудность преодолевается, если перейти к конечным базисам и приближенной реализации унитарных опе- раторов. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 21 / 36
- 60. Операторы, действующие на двух кубитах Теорема об универсальности двухкубитовых операторов Любой унитарный оператор точно реализуется в расширенном смысле в базисе B2 , состоящем из всех операторов, действующих на двух кубитах. План доказательства 1 Любой унитарный оператор композиция подкрученных транспозиций. 2 Любая подкрученная транспозиция реализуется в базисе, который содержит все операторы, действующие на одном кубите, и NOT-базис (NOT, c-NOT, cc-NOT). 3 Элемент Тоффоли cc-NOT реализуется в базисе B2 . М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 22 / 36
- 61. Операторы, действующие на двух кубитах Теорема об универсальности двухкубитовых операторов Любой унитарный оператор точно реализуется в расширенном смысле в базисе B2 , состоящем из всех операторов, действующих на двух кубитах. План доказательства 1 Любой унитарный оператор композиция подкрученных транспозиций. 2 Любая подкрученная транспозиция реализуется в базисе, который содержит все операторы, действующие на одном кубите, и NOT-базис (NOT, c-NOT, cc-NOT). 3 Элемент Тоффоли cc-NOT реализуется в базисе B2 . М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 22 / 36
- 62. Операторы, действующие на двух кубитах Теорема об универсальности двухкубитовых операторов Любой унитарный оператор точно реализуется в расширенном смысле в базисе B2 , состоящем из всех операторов, действующих на двух кубитах. План доказательства 1 Любой унитарный оператор композиция подкрученных транспозиций. 2 Любая подкрученная транспозиция реализуется в базисе, который содержит все операторы, действующие на одном кубите, и NOT-базис (NOT, c-NOT, cc-NOT). 3 Элемент Тоффоли cc-NOT реализуется в базисе B2 . М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 22 / 36
- 63. Операторы, действующие на двух кубитах Теорема об универсальности двухкубитовых операторов Любой унитарный оператор точно реализуется в расширенном смысле в базисе B2 , состоящем из всех операторов, действующих на двух кубитах. План доказательства 1 Любой унитарный оператор композиция подкрученных транспозиций. 2 Любая подкрученная транспозиция реализуется в базисе, который содержит все операторы, действующие на одном кубите, и NOT-базис (NOT, c-NOT, cc-NOT). 3 Элемент Тоффоли cc-NOT реализуется в базисе B2 . М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 22 / 36
- 64. Подкрученные транспозиции Определение Назовем подкрученной транспозицией унитарный оператор U : CM → CM , матрица которого имеет вид: 1 0 .................... 0 . . . . . 0 . . . . . . . . . . . . . . . . . 0 . 0 . . a 0 . . 0 b . . 0 0 . . 0 1 . . 0 . . . . . . 0 . . . . . . . . . . . . . . . . . . . . . . . . . . .. 0 . . 0 0 . . 1 . . . . . . 0 0 . . c 0 . . . . . . d . . 0 .. . . . . . . . . . . . . . . . . . . . . . . . . 0 0 ......................... 1 М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 23 / 36
- 65. Доказательство теоремы об универсальности: шаг 1 Лемма 1 Любой унитарный оператор U : CM → CM , где M 2, является композицией подкрученных транспозиций. Доказываем индукцией по порядку матрицы аналогично тому, как доказывается, что транспозиции порождают все перестановки. Наблюдение Для любых c1 , c2 существует такая унитарная матрица V размера 2 × 2, что c1 |c1 |2 + |c2 |2 V = . c2 0 Упражнение Докажите справедливость этого наблюдения. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 24 / 36
- 66. Доказательство теоремы об универсальности: шаг 1 Лемма 1 Любой унитарный оператор U : CM → CM , где M 2, является композицией подкрученных транспозиций. Доказываем индукцией по порядку матрицы аналогично тому, как доказывается, что транспозиции порождают все перестановки. Наблюдение Для любых c1 , c2 существует такая унитарная матрица V размера 2 × 2, что c1 |c1 |2 + |c2 |2 V = . c2 0 Упражнение Докажите справедливость этого наблюдения. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 24 / 36
- 67. Доказательство теоремы об универсальности: шаг 1 Лемма 1 Любой унитарный оператор U : CM → CM , где M 2, является композицией подкрученных транспозиций. Доказываем индукцией по порядку матрицы аналогично тому, как доказывается, что транспозиции порождают все перестановки. Наблюдение Для любых c1 , c2 существует такая унитарная матрица V размера 2 × 2, что c1 |c1 |2 + |c2 |2 V = . c2 0 Упражнение Докажите справедливость этого наблюдения. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 24 / 36
- 68. Доказательство теоремы об универсальности: шаг 1 Лемма 1 Любой унитарный оператор U : CM → CM , где M 2, является композицией подкрученных транспозиций. Доказываем индукцией по порядку матрицы аналогично тому, как доказывается, что транспозиции порождают все перестановки. Наблюдение Для любых c1 , c2 существует такая унитарная матрица V размера 2 × 2, что c1 |c1 |2 + |c2 |2 V = . c2 0 Упражнение Докажите справедливость этого наблюдения. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 24 / 36
- 69. Доказательство теоремы об универсальности: шаг 1 Для любого |ξ ∈ CM существует последовательность V (1) , . . . , V (M−1) такая, что V (1) · . . . · V (M−1) |ξ = |1 , где V (s) подкрученная транспозиция, действующая на C(|s , |s + 1 ). Поэтому умножениями на подкрученные транспозиции можно перевести первый столбец любой унитарной матрицы в единичный. Из условия унитарности следует, что и первая строка станет единичной: 1 0M−1 V (1) · . . . · V (M−1) U = 0M−1 U1 Теперь применим индуктивное предположение к U1 . М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 25 / 36
- 70. Доказательство теоремы об универсальности: шаг 1 Для любого |ξ ∈ CM существует последовательность V (1) , . . . , V (M−1) такая, что V (1) · . . . · V (M−1) |ξ = |1 , где V (s) подкрученная транспозиция, действующая на C(|s , |s + 1 ). Поэтому умножениями на подкрученные транспозиции можно перевести первый столбец любой унитарной матрицы в единичный. Из условия унитарности следует, что и первая строка станет единичной: 1 0M−1 V (1) · . . . · V (M−1) U = 0M−1 U1 Теперь применим индуктивное предположение к U1 . М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 25 / 36
- 71. Доказательство теоремы об универсальности: шаг 1 Для любого |ξ ∈ CM существует последовательность V (1) , . . . , V (M−1) такая, что V (1) · . . . · V (M−1) |ξ = |1 , где V (s) подкрученная транспозиция, действующая на C(|s , |s + 1 ). Поэтому умножениями на подкрученные транспозиции можно перевести первый столбец любой унитарной матрицы в единичный. Из условия унитарности следует, что и первая строка станет единичной: 1 0M−1 V (1) · . . . · V (M−1) U = 0M−1 U1 Теперь применим индуктивное предположение к U1 . М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 25 / 36
- 72. Доказательство теоремы об универсальности: шаг 1 Для любого |ξ ∈ CM существует последовательность V (1) , . . . , V (M−1) такая, что V (1) · . . . · V (M−1) |ξ = |1 , где V (s) подкрученная транспозиция, действующая на C(|s , |s + 1 ). Поэтому умножениями на подкрученные транспозиции можно перевести первый столбец любой унитарной матрицы в единичный. Из условия унитарности следует, что и первая строка станет единичной: 1 0M−1 V (1) · . . . · V (M−1) U = 0M−1 U1 Теперь применим индуктивное предположение к U1 . М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 25 / 36
- 73. Несколько управляющих кубитов Определение |x1 , . . . , xn ⊗ U|ψ , если x1 x2 . . . xn = 1; c(n) -U : |x1 , . . . , xn ⊗ |ψ = |x1 , . . . , xn ⊗ |ψ , иначе. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 26 / 36
- 74. Несколько управляющих кубитов Определение |x1 , . . . , xn ⊗ U|ψ , если x1 x2 . . . xn = 1; c(n) -U : |x1 , . . . , xn ⊗ |ψ = |x1 , . . . , xn ⊗ |ψ , иначе. Реализация c(n) -U в базисе B2 ∪ {NOT, c-NOT, cc-NOT} |x1 |x1 |x2 |x2 ... ... |xn |xn x1 x2 . . . xn |0 P P −1 |0 |0 |0 |0 |0 |0 |0 |0 |0 |ψ U U |ψ М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 26 / 36
- 75. Доказательство теоремы об универсальности: шаг 2 Операторы c(n) -U являются подкрученными транспозициями, действующими на пространстве C(|1 . . . 10 , |1 . . . 11 ). Любая другая подкрученная транспозиция T получается из c(n) -U сопряжением перестановочным оператором: T = Pc(n) -UP −1 , P : |1 . . . 10 → |x , P : |1 . . . 11 → |y . Оператор P реализуется в NOT-базисе в расширенном смысле. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 27 / 36
- 76. Доказательство теоремы об универсальности: шаг 2 Операторы c(n) -U являются подкрученными транспозициями, действующими на пространстве C(|1 . . . 10 , |1 . . . 11 ). Любая другая подкрученная транспозиция T получается из c(n) -U сопряжением перестановочным оператором: T = Pc(n) -UP −1 , P : |1 . . . 10 → |x , P : |1 . . . 11 → |y . Оператор P реализуется в NOT-базисе в расширенном смысле. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 27 / 36
- 77. Доказательство теоремы об универсальности: шаг 2 Операторы c(n) -U являются подкрученными транспозициями, действующими на пространстве C(|1 . . . 10 , |1 . . . 11 ). Любая другая подкрученная транспозиция T получается из c(n) -U сопряжением перестановочным оператором: T = Pc(n) -UP −1 , P : |1 . . . 10 → |x , P : |1 . . . 11 → |y . Оператор P реализуется в NOT-базисе в расширенном смысле. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 27 / 36
- 78. Доказательство теоремы об универсальности: шаг 3 Элемент Тоффоли c(2) -σx в базисе B2 i −1 −1 B A B A 1 −i −1 0 1 где A = √ ; B= 2 1 i −1 0 Упражнение Проверьте, что A2 = −I , B 2 = −I , ABA−1 B −1 = −iσx . М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 28 / 36
- 79. Доказательство теоремы об универсальности: шаг 3 Элемент Тоффоли c(2) -σx в базисе B2 i −1 −1 B A B A 1 −i −1 0 1 где A = √ ; B= 2 1 i −1 0 Упражнение Проверьте, что A2 = −I , B 2 = −I , ABA−1 B −1 = −iσx . М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 28 / 36
- 80. Об избыточности базиса B2 Из доказательства теоремы видно, что любой унитарный оператор выражается в базисе, который содержит все однокубитовые операторы и все операторы вида c-U, где U однокубитовый. Оказывается, из второй группы операторов достаточно оставить только c-NOT = c-σx . М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 29 / 36
- 81. Об избыточности базиса B2 Из доказательства теоремы видно, что любой унитарный оператор выражается в базисе, который содержит все однокубитовые операторы и все операторы вида c-U, где U однокубитовый. Оказывается, из второй группы операторов достаточно оставить только c-NOT = c-σx . М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 29 / 36
- 82. Об избыточности базиса B2 Из доказательства теоремы видно, что любой унитарный оператор выражается в базисе, который содержит все однокубитовые операторы и все операторы вида c-U, где U однокубитовый. Оказывается, из второй группы операторов достаточно оставить только c-NOT = c-σx . Теорема 2 Любой оператор вида c-U представляется в виде K(ϑ) B −1 σx B A−1 σx A 1 0 где K (ϑ) = 0 e iϑ М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 29 / 36
- 83. План 1 Трудоемкость квантового вычисления 2 Точная реализация унитарных операторов квантовыми схемами Обратимые вычисления: мостик между классическими и квантовыми Базис из операторов, действующих на одном кубите Базис из операторов, действующих на двух кубитах 3 Об унитарных преобразованиях одного кубита М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 30 / 36
- 84. Еще раз о сфере Блоха Матрицы Паули: 0 1 0 −i 1 0 σx = , σy = , σz = . 1 0 i 0 0 −1 Утверждение Если |ψ = a|0 + b|1 состояние кубита, то 1 |ψ ψ| = (I + xσx + y σy + zσz ), x 2 + y 2 + z 2 = 1, x, y , z ∈ R. 2 Без ограничения общности a ∈ [0; 1] (общий фазовый множитель ненаблюдаем). Тогда a = cos(θ/2), b = e iϕ sin(θ/2), θ ∈ [0; π]; ϕ ∈ [0; 2π); x = cos ϕ sin θ; y = sin ϕ sin θ; z = cos θ (сферические координаты). М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 31 / 36
- 85. Еще раз о сфере Блоха Матрицы Паули: 0 1 0 −i 1 0 σx = , σy = , σz = . 1 0 i 0 0 −1 Утверждение Если |ψ = a|0 + b|1 состояние кубита, то 1 |ψ ψ| = (I + xσx + y σy + zσz ), x 2 + y 2 + z 2 = 1, x, y , z ∈ R. 2 Без ограничения общности a ∈ [0; 1] (общий фазовый множитель ненаблюдаем). Тогда a = cos(θ/2), b = e iϕ sin(θ/2), θ ∈ [0; π]; ϕ ∈ [0; 2π); x = cos ϕ sin θ; y = sin ϕ sin θ; z = cos θ (сферические координаты). М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 31 / 36
- 86. Еще раз о сфере Блоха Матрицы Паули: 0 1 0 −i 1 0 σx = , σy = , σz = . 1 0 i 0 0 −1 Утверждение Если |ψ = a|0 + b|1 состояние кубита, то 1 |ψ ψ| = (I + xσx + y σy + zσz ), x 2 + y 2 + z 2 = 1, x, y , z ∈ R. 2 Без ограничения общности a ∈ [0; 1] (общий фазовый множитель ненаблюдаем). Тогда a = cos(θ/2), b = e iϕ sin(θ/2), θ ∈ [0; π]; ϕ ∈ [0; 2π); x = cos ϕ sin θ; y = sin ϕ sin θ; z = cos θ (сферические координаты). М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 31 / 36
- 87. Проверка утверждения cos(θ/2) |ψ ψ| = cos(θ/2) e −iϕ sin(θ/2) = e iϕ sin(θ/2) cos2 (θ/2) e −iϕ cos(θ/2) sin(θ/2) = = e iϕ cos(θ/2) sin(θ/2) sin2 (θ/2) 11 0 1 1 0 = + cos θ + 20 1 2 0 −1 1 0 1 1 0 −i + cos ϕ sin θ + sin ϕ sin θ = 2 1 0 2 i 0 1 = (I + xσx + y σy + zσz ) 2 М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 32 / 36
- 88. Проверка утверждения cos(θ/2) |ψ ψ| = cos(θ/2) e −iϕ sin(θ/2) = e iϕ sin(θ/2) cos2 (θ/2) e −iϕ cos(θ/2) sin(θ/2) = = e iϕ cos(θ/2) sin(θ/2) sin2 (θ/2) 11 0 1 1 0 = + cos θ + 20 1 2 0 −1 1 0 1 1 0 −i + cos ϕ sin θ + sin ϕ sin θ = 2 1 0 2 i 0 1 = (I + xσx + y σy + zσz ) 2 М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 32 / 36
- 89. Проверка утверждения cos(θ/2) |ψ ψ| = cos(θ/2) e −iϕ sin(θ/2) = e iϕ sin(θ/2) cos2 (θ/2) e −iϕ cos(θ/2) sin(θ/2) = = e iϕ cos(θ/2) sin(θ/2) sin2 (θ/2) 1 1 0 1 1 0 = + cos θ + 0 1 2 2 0 −1 1 0 1 1 0 −i + cos ϕ sin θ + sin ϕ sin θ = 2 1 0 2 i 0 1 = (I + xσx + y σy + zσz ) 2 М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 32 / 36
- 90. Проверка утверждения cos(θ/2) |ψ ψ| = cos(θ/2) e −iϕ sin(θ/2) = e iϕ sin(θ/2) cos2 (θ/2) e −iϕ cos(θ/2) sin(θ/2) = = e iϕ cos(θ/2) sin(θ/2) sin2 (θ/2) 11 0 1 1 0 = + cos θ + 20 1 2 0 −1 1 0 1 1 0 −i + cos ϕ sin θ + sin ϕ sin θ = 2 1 0 2 i 0 1 = (I + xσx + y σy + zσz ) 2 М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 32 / 36
- 91. Проверка утверждения cos(θ/2) |ψ ψ| = cos(θ/2) e −iϕ sin(θ/2) = e iϕ sin(θ/2) cos2 (θ/2) e −iϕ cos(θ/2) sin(θ/2) = = e iϕ cos(θ/2) sin(θ/2) sin2 (θ/2) 11 0 1 1 0 = + cos θ + 20 1 2 0 −1 1 0 1 1 0 −i + cos ϕ sin θ + sin ϕ sin θ = 2 1 0 2 i 0 1 = (I + xσx + y σy + zσz ) 2 М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 32 / 36
- 92. Скалярное произведение и эрмитово произведение Пусть |ψ на сфере Блоха попадает в (x , y , z ), |ξ в (x , y , z ). Матрицы Паули (включая единичную) ортогональны относительно произведения Фробениуса: 1 Tr(σα σβ ) = δαβ (упражнение). 2 Поэтому 1 | ψ|ξ |2 = Tr(|ψ ψ| |ξ ξ|) = (1 + x x + y y + z z ). 2 Следствие 1: пара ортогональных состояний попадает на сфере Блоха в диаметрально противоположные точки. Следствие 2: унитарное преобразование действует на сфере Блоха по правилу U : |ψ ψ| → U|ψ ψ|U † и это действие движение трехмерного пространства, сохраняющее центр сферы. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 33 / 36
- 93. Скалярное произведение и эрмитово произведение Пусть |ψ на сфере Блоха попадает в (x , y , z ), |ξ в (x , y , z ). Матрицы Паули (включая единичную) ортогональны относительно произведения Фробениуса: 1 Tr(σα σβ ) = δαβ (упражнение). 2 Поэтому 1 | ψ|ξ |2 = Tr(|ψ ψ| |ξ ξ|) = (1 + x x + y y + z z ). 2 Следствие 1: пара ортогональных состояний попадает на сфере Блоха в диаметрально противоположные точки. Следствие 2: унитарное преобразование действует на сфере Блоха по правилу U : |ψ ψ| → U|ψ ψ|U † и это действие движение трехмерного пространства, сохраняющее центр сферы. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 33 / 36
- 94. Скалярное произведение и эрмитово произведение Пусть |ψ на сфере Блоха попадает в (x , y , z ), |ξ в (x , y , z ). Матрицы Паули (включая единичную) ортогональны относительно произведения Фробениуса: 1 Tr(σα σβ ) = δαβ (упражнение). 2 Поэтому 1 | ψ|ξ |2 = Tr(|ψ ψ| |ξ ξ|) = (1 + x x + y y + z z ). 2 Следствие 1: пара ортогональных состояний попадает на сфере Блоха в диаметрально противоположные точки. Следствие 2: унитарное преобразование действует на сфере Блоха по правилу U : |ψ ψ| → U|ψ ψ|U † и это действие движение трехмерного пространства, сохраняющее центр сферы. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 33 / 36
- 95. Скалярное произведение и эрмитово произведение Пусть |ψ на сфере Блоха попадает в (x , y , z ), |ξ в (x , y , z ). Матрицы Паули (включая единичную) ортогональны относительно произведения Фробениуса: 1 Tr(σα σβ ) = δαβ (упражнение). 2 Поэтому 1 | ψ|ξ |2 = Tr(|ψ ψ| |ξ ξ|) = (1 + x x + y y + z z ). 2 Следствие 1: пара ортогональных состояний попадает на сфере Блоха в диаметрально противоположные точки. Следствие 2: унитарное преобразование действует на сфере Блоха по правилу U : |ψ ψ| → U|ψ ψ|U † и это действие движение трехмерного пространства, сохраняющее центр сферы. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 33 / 36
- 96. Скалярное произведение и эрмитово произведение Пусть |ψ на сфере Блоха попадает в (x , y , z ), |ξ в (x , y , z ). Матрицы Паули (включая единичную) ортогональны относительно произведения Фробениуса: 1 Tr(σα σβ ) = δαβ (упражнение). 2 Поэтому 1 | ψ|ξ |2 = Tr(|ψ ψ| |ξ ξ|) = (1 + x x + y y + z z ). 2 Следствие 1: пара ортогональных состояний попадает на сфере Блоха в диаметрально противоположные точки. Следствие 2: унитарное преобразование действует на сфере Блоха по правилу U : |ψ ψ| → U|ψ ψ|U † и это действие движение трехмерного пространства, сохраняющее центр сферы. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 33 / 36
- 97. Действие унитарного оператора на сфере Блоха: поворот Скалярные операторы |ψ → e iα |ψ действуют на сфере Блоха тождественно. Верно и обратное: если унитарный оператор U действует на сфере Блоха тождественно, то каждый вектор собственный, а оператор скалярный. Любой унитарный оператор имеет ортонормированный базис из собственных векторов. Соответствующая пара точек на сфере Блоха не меняется при действии оператора. Нетривиальное действие унитарного оператора на сфере Блоха движение, у которого есть ровно одна пара неподвижных точек на сфере Блоха. Это поворот. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 34 / 36
- 98. Действие унитарного оператора на сфере Блоха: поворот Скалярные операторы |ψ → e iα |ψ действуют на сфере Блоха тождественно. Верно и обратное: если унитарный оператор U действует на сфере Блоха тождественно, то каждый вектор собственный, а оператор скалярный. Любой унитарный оператор имеет ортонормированный базис из собственных векторов. Соответствующая пара точек на сфере Блоха не меняется при действии оператора. Нетривиальное действие унитарного оператора на сфере Блоха движение, у которого есть ровно одна пара неподвижных точек на сфере Блоха. Это поворот. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 34 / 36
- 99. Действие унитарного оператора на сфере Блоха: поворот Скалярные операторы |ψ → e iα |ψ действуют на сфере Блоха тождественно. Верно и обратное: если унитарный оператор U действует на сфере Блоха тождественно, то каждый вектор собственный, а оператор скалярный. Любой унитарный оператор имеет ортонормированный базис из собственных векторов. Соответствующая пара точек на сфере Блоха не меняется при действии оператора. Нетривиальное действие унитарного оператора на сфере Блоха движение, у которого есть ровно одна пара неподвижных точек на сфере Блоха. Это поворот. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 34 / 36
- 100. Действие унитарного оператора на сфере Блоха: поворот Скалярные операторы |ψ → e iα |ψ действуют на сфере Блоха тождественно. Верно и обратное: если унитарный оператор U действует на сфере Блоха тождественно, то каждый вектор собственный, а оператор скалярный. Любой унитарный оператор имеет ортонормированный базис из собственных векторов. Соответствующая пара точек на сфере Блоха не меняется при действии оператора. Нетривиальное действие унитарного оператора на сфере Блоха движение, у которого есть ровно одна пара неподвижных точек на сфере Блоха. Это поворот. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 34 / 36
- 101. Действие унитарного оператора на сфере Блоха: поворот Скалярные операторы |ψ → e iα |ψ действуют на сфере Блоха тождественно. Верно и обратное: если унитарный оператор U действует на сфере Блоха тождественно, то каждый вектор собственный, а оператор скалярный. Любой унитарный оператор имеет ортонормированный базис из собственных векторов. Соответствующая пара точек на сфере Блоха не меняется при действии оператора. Нетривиальное действие унитарного оператора на сфере Блоха движение, у которого есть ровно одна пара неподвижных точек на сфере Блоха. Это поворот. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 34 / 36
- 102. О матрицах Паули 2 2 2 Поскольку σx = σy = σz = I , матрицы Паули повороты на π. Так как 1 † 1 σx (I + σx )σx = (I + σx ), 2 2 1 † 1 σy (I + σy )σy = (I + σy ), 2 2 1 † 1 σz (I + σz )σz = (I + σz ), 2 2 σx , σy , σz повороты вокруг осей Ox, Oy , Oz соответственно. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 35 / 36
- 103. О матрицах Паули 2 2 2 Поскольку σx = σy = σz = I , матрицы Паули повороты на π. Так как 1 † 1 σx (I + σx )σx = (I + σx ), 2 2 1 † 1 σy (I + σy )σy = (I + σy ), 2 2 1 † 1 σz (I + σz )σz = (I + σz ), 2 2 σx , σy , σz повороты вокруг осей Ox, Oy , Oz соответственно. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 35 / 36
- 104. Доказательство теоремы 2 Теорема 2 Любой оператор вида c-U представляется в виде K(ϑ) B −1 σx B A−1 σx A 1 0 где K (ϑ) = 0 e iϑ Достаточно доказать, что для любого U есть представление вида U = e iϑ Aσx A−1 Bσx B −1 . Задача Докажите, что любой поворот трехмерного пространства является композицией двух поворотов на угол π. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 36 / 36
- 105. Доказательство теоремы 2 Теорема 2 Любой оператор вида c-U представляется в виде K(ϑ) B −1 σx B A−1 σx A 1 0 где K (ϑ) = 0 e iϑ Достаточно доказать, что для любого U есть представление вида U = e iϑ Aσx A−1 Bσx B −1 . Задача Докажите, что любой поворот трехмерного пространства является композицией двух поворотов на угол π. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 36 / 36
- 106. Доказательство теоремы 2 Теорема 2 Любой оператор вида c-U представляется в виде K(ϑ) B −1 σx B A−1 σx A 1 0 где K (ϑ) = 0 e iϑ Достаточно доказать, что для любого U есть представление вида U = e iϑ Aσx A−1 Bσx B −1 . Задача Докажите, что любой поворот трехмерного пространства является композицией двух поворотов на угол π. М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 36 / 36





![Квантовая схема над базисом B: определение
...
...
U4 ...
...
U1 ...
...
...
...
U3 ...
U2 ... U
...
Квантовая схема
Последовательность операторов
U1 [S1 ], U2 [S2 ], . . . , U [S ],
где Uk ∈ B, Sk ⊆ {1, . . . , n}, n количество используемых кубитов.
М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 5 / 36](https://image.slidesharecdn.com/20110409quantumalgorithmsvyalilecture06-110409120456-phpapp02/85/20110409-quantum-algorithms_vyali_lecture06-8-320.jpg)
![Матричные элементы U[S]
Пусть
U= ux,y |x y |,
x,y ∈{0,1}d
S = {j1 , . . . , jd }.
Обозначим x[S] подпоследовательность битов, стоящих на местах из
множества S.
Тогда
U[S] = ux[S],y [S] |x y |.
¯ ¯
x,y ∈{0,1}n :x[S]=y [S]
М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 6 / 36](https://image.slidesharecdn.com/20110409quantumalgorithmsvyalilecture06-110409120456-phpapp02/85/20110409-quantum-algorithms_vyali_lecture06-9-320.jpg)
![Матричные элементы U[S]
Пусть
U= ux,y |x y |,
x,y ∈{0,1}d
S = {j1 , . . . , jd }.
Обозначим x[S] подпоследовательность битов, стоящих на местах из
множества S.
Тогда
U[S] = ux[S],y [S] |x y |.
¯ ¯
x,y ∈{0,1}n :x[S]=y [S]
М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 6 / 36](https://image.slidesharecdn.com/20110409quantumalgorithmsvyalilecture06-110409120456-phpapp02/85/20110409-quantum-algorithms_vyali_lecture06-10-320.jpg)
![Матричные элементы U[S]
Пусть
U= ux,y |x y |,
x,y ∈{0,1}d
S = {j1 , . . . , jd }.
Обозначим x[S] подпоследовательность битов, стоящих на местах из
множества S.
Тогда
U[S] = ux[S],y [S] |x y |.
¯ ¯
x,y ∈{0,1}n :x[S]=y [S]
М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 6 / 36](https://image.slidesharecdn.com/20110409quantumalgorithmsvyalilecture06-110409120456-phpapp02/85/20110409-quantum-algorithms_vyali_lecture06-11-320.jpg)



















![Определения
Схема U1 [S1 ], U2 [S2 ], . . . , U [S ] реализует оператор
U = U [S ] . . . U2 [S2 ]U1 [S1 ]
(обратите внимание на порядок).
Схема U1 [S1 ], U2 [S2 ], . . . , U [S ] реализует оператор U в расширенном
смысле, если
U [S ] . . . U2 [S2 ]U1 [S1 ] : |ψ ⊗ |0N → U|ψ ⊗ |0N
для всех |ψ ∈ (C2 )⊗n .
Сложностью реализации оператора U (в расширенном смысле) в
базисе B называется наименьший размер схемы в базисе B,
реализующей U (в расширенном смысле).
Сложность бесконечна, если реализации не существует.
М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 13 / 36](https://image.slidesharecdn.com/20110409quantumalgorithmsvyalilecture06-110409120456-phpapp02/85/20110409-quantum-algorithms_vyali_lecture06-35-320.jpg)
![Определения
Схема U1 [S1 ], U2 [S2 ], . . . , U [S ] реализует оператор
U = U [S ] . . . U2 [S2 ]U1 [S1 ]
(обратите внимание на порядок).
Схема U1 [S1 ], U2 [S2 ], . . . , U [S ] реализует оператор U в расширенном
смысле, если
U [S ] . . . U2 [S2 ]U1 [S1 ] : |ψ ⊗ |0N → U|ψ ⊗ |0N
для всех |ψ ∈ (C2 )⊗n .
Сложностью реализации оператора U (в расширенном смысле) в
базисе B называется наименьший размер схемы в базисе B,
реализующей U (в расширенном смысле).
Сложность бесконечна, если реализации не существует.
М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 13 / 36](https://image.slidesharecdn.com/20110409quantumalgorithmsvyalilecture06-110409120456-phpapp02/85/20110409-quantum-algorithms_vyali_lecture06-36-320.jpg)
![Определения
Схема U1 [S1 ], U2 [S2 ], . . . , U [S ] реализует оператор
U = U [S ] . . . U2 [S2 ]U1 [S1 ]
(обратите внимание на порядок).
Схема U1 [S1 ], U2 [S2 ], . . . , U [S ] реализует оператор U в расширенном
смысле, если
U [S ] . . . U2 [S2 ]U1 [S1 ] : |ψ ⊗ |0N → U|ψ ⊗ |0N
для всех |ψ ∈ (C2 )⊗n .
Сложностью реализации оператора U (в расширенном смысле) в
базисе B называется наименьший размер схемы в базисе B,
реализующей U (в расширенном смысле).
Сложность бесконечна, если реализации не существует.
М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 13 / 36](https://image.slidesharecdn.com/20110409quantumalgorithmsvyalilecture06-110409120456-phpapp02/85/20110409-quantum-algorithms_vyali_lecture06-37-320.jpg)
![О реализации в расширенном смысле
Основная цель моделировать вероятностные распределения,
порождаемые унитарными операторами.
Условие реализации в расширенном смысле гарантирует, что при
измерении состояния U [S ] . . . U2 [S2 ]U1 [S1 ](|ψ ⊗ |0N ) значения
кубитов первого регистра распределены также, как при измерении
состояния U|ψ .
Достаточны и более слабые условия, например,
U [S ] . . . U2 [S2 ]U1 [S1 ] : |ψ ⊗ |0N → U|ψ ⊗ V |ψ . (∗)
Однако, это условие не слишком добавляет общности.
Задача
Докажите, что из выполнения (∗) следует V |ψ = |ξ для любого ψ.
Дополнительным преимуществом условия реализации в расширенном
смысле является сохранение этого свойства при композициях.
М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 14 / 36](https://image.slidesharecdn.com/20110409quantumalgorithmsvyalilecture06-110409120456-phpapp02/85/20110409-quantum-algorithms_vyali_lecture06-38-320.jpg)












































![Еще раз о сфере Блоха
Матрицы Паули:
0 1 0 −i 1 0
σx = , σy = , σz = .
1 0 i 0 0 −1
Утверждение
Если |ψ = a|0 + b|1 состояние кубита, то
1
|ψ ψ| = (I + xσx + y σy + zσz ), x 2 + y 2 + z 2 = 1, x, y , z ∈ R.
2
Без ограничения общности a ∈ [0; 1] (общий фазовый множитель
ненаблюдаем).
Тогда a = cos(θ/2), b = e iϕ sin(θ/2), θ ∈ [0; π]; ϕ ∈ [0; 2π);
x = cos ϕ sin θ; y = sin ϕ sin θ; z = cos θ
(сферические координаты).
М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 31 / 36](https://image.slidesharecdn.com/20110409quantumalgorithmsvyalilecture06-110409120456-phpapp02/85/20110409-quantum-algorithms_vyali_lecture06-84-320.jpg)
![Еще раз о сфере Блоха
Матрицы Паули:
0 1 0 −i 1 0
σx = , σy = , σz = .
1 0 i 0 0 −1
Утверждение
Если |ψ = a|0 + b|1 состояние кубита, то
1
|ψ ψ| = (I + xσx + y σy + zσz ), x 2 + y 2 + z 2 = 1, x, y , z ∈ R.
2
Без ограничения общности a ∈ [0; 1] (общий фазовый множитель
ненаблюдаем).
Тогда a = cos(θ/2), b = e iϕ sin(θ/2), θ ∈ [0; π]; ϕ ∈ [0; 2π);
x = cos ϕ sin θ; y = sin ϕ sin θ; z = cos θ
(сферические координаты).
М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 31 / 36](https://image.slidesharecdn.com/20110409quantumalgorithmsvyalilecture06-110409120456-phpapp02/85/20110409-quantum-algorithms_vyali_lecture06-85-320.jpg)
![Еще раз о сфере Блоха
Матрицы Паули:
0 1 0 −i 1 0
σx = , σy = , σz = .
1 0 i 0 0 −1
Утверждение
Если |ψ = a|0 + b|1 состояние кубита, то
1
|ψ ψ| = (I + xσx + y σy + zσz ), x 2 + y 2 + z 2 = 1, x, y , z ∈ R.
2
Без ограничения общности a ∈ [0; 1] (общий фазовый множитель
ненаблюдаем).
Тогда a = cos(θ/2), b = e iϕ sin(θ/2), θ ∈ [0; π]; ϕ ∈ [0; 2π);
x = cos ϕ sin θ; y = sin ϕ sin θ; z = cos θ
(сферические координаты).
М. Вялый (ВЦ РАН) Лекция 6: Квантовые схемы Санкт-Петербург, 2011 31 / 36](https://image.slidesharecdn.com/20110409quantumalgorithmsvyalilecture06-110409120456-phpapp02/85/20110409-quantum-algorithms_vyali_lecture06-86-320.jpg)



















