2.ppt

Chapter 2 AC to DC Converters
Outline
2.1 Single-phase controlled rectifier
2.2 Three-phase controlled rectifier
2.3 Effect of transformer leakage inductance on rectifier circuits
2.4 Capacitor-filtered uncontrolled rectifier
2.5 Harmonics and power factor of rectifier circuits
2.6 High power controlled rectifier
2.7 Inverter mode operation of rectifier circuit
2.8 Thyristor-DC motor system
2.9 Realization of phase-control in rectifier

2.1 Single- phase controlled (controllable) rectifier
2.1.1 Single-phase half-wave controlled rectifier
Resistive load
T
VT
R
a)
u1
u2
uVT
ud
id
0 t1  2
 t
u2
ug
ud
uVT
 
0
b)
c)
d)
e)
0
0
 t
 t
 t













 2
cos
1
45
.
0
)
cos
1
(
2
2
)
(
sin
2
2
1
2
2
2
d U
U
t
td
U
U
（2-1）

Inductive (resistor-inductor) load
a)
u1
T
VT
R
L
u2
uVT
ud
id
u2
0 t1
 2
 t
ug
0
ud
0
id
0
uVT
0


b)
c)
d)
e)
f)
+ +
 t
 t
 t
 t

Basic thought process of time-domain analysis for power electronic
circuits
The time- domain behavior of a power electronic circuit is actually the
combination of consecutive transients of the different linear circuits
when the power semiconductor devices are in different states.
a) b)
VT
R
L
VT
R
L
u2 u2
t
U
Ri
t
i
L 
sin
2
d
d
2
d
d


ωt= a ，id=0
)
sin(
2
)
sin(
2 2
)
(
2
d 













t
Z
U
e
Z
U
i
t
L
R
（2-2）
（2-3）

Single- phase half- wave controlled rectifier with freewheeling diode
load (L is large enough) Inductive
a)
L
T VT
R
u1
u2
uVT
ud
VDR
id
iVD
u2
ud
id
uVT
iVT
Id
Id
t
O
O
O
O
O
O
- +
b)
iVDR
t
t
t
t
t
g)
c)
e)
f)
d)
T1

Maximum forward voltage, maximum reverse voltage
Disadvantages:
–Only single pulse in one line cycle
–DC component in the transformer current
d
dVT
2
I
I


 

d
2
d
VT
2
)
(
2
1
I
t
d
I
I









 
d
2
2
d
VD
2
)
(
2
1
R
I
t
d
I
I










 

d
dVD
2
R
I
I


 

（2-5）
（2-6）
（2-7）
（2-8）

2.1.2 Single- phase bridge fully-controlled rectifier
 Resistive load
  t
0
0
0
i2
ud
id
b)
c)
d)
ud
(id
)
 
R
T
u1 u2
a)
i2
a
b
VT3
ud
i
d
uVT
1,4
 t
 t
VT4
VT1
VT2

Average output (rectified) voltage:
Average output current:
For thyristor:
For transformer:













 2
cos
1
9
.
0
2
cos
1
2
2
)
(
d
sin
2
1
2
2
2
d U
U
t
t
U
U （2-9）
（2-10）
2
cos
1
9
.
0
2
cos
1
2
2 2
2
d
d








R
U
R
U
R
U
I
（2-11）
2
cos
1
45
.
0
2
1 2
d
dVT




R
U
I
I













  2
sin
2
1
2
)
(
d
)
sin
2
(
2
1 2
2
2
VT
R
U
t
t
R
U
I （2-12）














  2
sin
2
1
)
(
)
sin
2
(
1 2
2
2
2
R
U
t
d
t
R
U
I
I (2-13)

 Inductive load (L is large enough)
 t
 t
 t
 t
 t
 t
 t







u2
ud
id
Id
Id
Id
Id
Id
iVT1,4
iVT2,3
uVT1,4
i2
,
b)
R
T
u1 u2
a)
i2
a
b
VT3
ud
i
d
VT4
VT1
VT2

 Electro- motive-force (EMF) load With resistor














cos
9
.
0
cos
2
2
)
(
d
sin
2
1
2
2
2
d U
U
t
t
U
U （2-15）
a) b)
R
E
id
ud id
O
E
ud
t
Id
O t
  

 With resistor and inductor
When L is large enough, the output voltage and current waveforms are the
same as ordinary inductive load.
When L is at a critical value
O
ud
0
E
id
 t
 t


 =
dmin
2
3
dmin
2
10
87
.
2
2
2
I
U
I
U
L 



 （2-17）

2.1.3 Single- phase full- wave controlled rectifier
a) b)
u1
T
R
u2
u2
i1 VT1
VT2 ud
ud
i1
O
O
  t
t

2.1.4 Single- phase bridge half-controlled rectifier
a)
T a
b R
L
O
b)
u2
i2
ud
id
VT
1
VT
2
VD
3
VD
4
VD
R
u2
O
ud
id Id
O
O
O
O
O
i2
Id
Id
Id
Id
Id

t
t
t
t
t
t
t



iVT
1
iVD
4
iVT
2
iVD
3
iVD
R

 Another single- phase bridge half-controlled rectifier
Comparison with previous circuit:
–No need for additional freewheeling diode
–Isolation is necessary between the drive circuits of the two thyristors
load
T
u2
VT2 VT4
VT1 VT3

Summary of some important points in analysis
When analyzing a thyristor circuit, start from a diode circuit with the same
topology. The behavior of the diode circuit is exactly the same as the
thyristor circuit when firing angle is 0.
A power electronic circuit can be considered as different linear circuits
when the power semiconductor devices are in different states. The
time- domain behavior of the power electronic circuit is actually the
combination of consecutive transients of the different linear circuits.
Take different principle when dealing with different load
– For resistive load: current waveform of a resistor is the same as the
voltage waveform
–For inductive load with a large inductor: the inductor current can
be considered constant

2.2 Three- phase controlled (controllable) rectifier
2.2.1 Three- phase half- wave controlled rectifier
Resistive load, α= 0º
a
b
c
T
R
ud
id
VT2
VT1
VT3
u2
O
O
O
uab uac
O
iVT1
uVT
1
 t
 t
 t
 t
 t
u a u b u c
u G
u d
 t1  t2  t3
Common-cathode connection
Natural commutation point

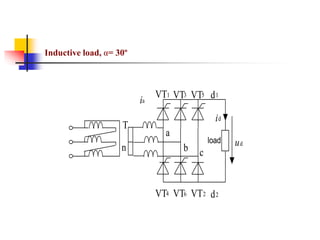
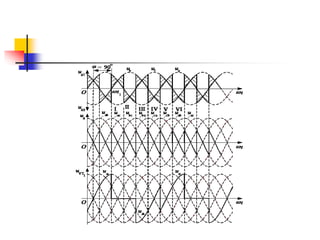
u2
ua ub uc
O
O
O t
O
t
O
t
uG
ud
uab uac
t1
iVT
1
uVT1 uac
t
t
a
b
c
T
R
ud
id
VT2
VT1
VT3

t
u2 ua ub uc
O
O
O
O
uG
ud
iVT
1
t
t
t
a
b
c
T
R
ud
id
VT2
VT1
VT3

Resistive load, quantitative analysis
When α≤ 30º , load current id is continuous.
When α > 30º , load current id is discontinuous.
Average load current
Thyristor voltages









 cos
17
.
1
cos
2
6
3
)
(
sin
2
3
2
1
2
2
6
5
6
2
d U
U
t
td
U
U 

 


（2-18）


















  
)
6
cos(
1
675
.
0
)
6
cos(
1
2
2
3
)
(
sin
2
3
2
1
2
6
2
d 









 U
t
td
U
U (2-19)
R
U
I d
d  （2-20）
0 30 60 90 120 150
0.4
0.8
1.2
1.17
3
2
1
/(°)
Ud/U2

 Inductive load, L is large enough

Thyristor voltage and currents, transformer current :









 cos
17
.
1
cos
2
6
3
)
(
sin
2
3
2
1
2
2
6
5
6
2
d U
U
t
td
U
U 

 


（2-18）
d
d
VT
2 577
.
0
3
1
I
I
I
I 

 d
VT
VT(AV) 368
.
0
57
.
1
I
I
I 

2
RM
FM 45
.
2 U
U
U 

（2-23）
（2-25）
（2-24）

2.2.2 Three- phase bridge fully-controlled rectifier
Circuit diagram
Common- cathode group and common- anode group of thyristors
Numbering of the 6 thyristors indicates the trigger sequence.
b
a
c
T
n
load
ia
id
ud
VT1 VT3 VT5
VT4 VT6 VT2 d2
d1