3.2

Thermal Physics
Topic 3.2 Thermal Properties of
Matter

Specific Heat Capacity
The amount of thermal energy needed to
raise the temperature of a mass of one
kilogram of a substance by one kelvin is
called the specific heat capacity, c.
The thermal energy required to raise mass
m with specific heat capacity c by a
temperature ∆T is
∆Q =mc∆T

Heat Capacity/Thermal Capacity
When substances undergo the same
temperature change they can store or release
different amounts of energy
They have different Heat Capacities
Heat capacity = ∆Q / ∆T in JK-1
∀ ∆Q = the change in thermal energy in joules
∀ ∆T = the change in temperature in Kelvin
Defined as the amount of energy to change
the temperature of a body by unit
temperature
Applies to a specific BODY

Heat Capacity - 2
A body with a high heat capacity will take in
thermal energy at a slower rate than a
substance with a low heat capacity because it
needs more time to absorb a greater quantity
of thermal energy
They also cool more slowly because they give
out thermal energy at a slower rate

Specific Heat Capacity
Defined as the amount of thermal energy
required to produce unit temperature rise in
unit mass of the MATERIAL
Unit mass is normally 1kg, and unit
temperature rise is normally 1K
Specific Heat Capacity = ∆Q / (m∆T)
in J kg -1
K-1
• where m is the mass of the material

For an object made of 1specific material
then with specific heat capacity=c
Heat Capacity = m x Specific Heat
Capacity
C=mc
Q=C∆T

Example 1
When a car brakes, an amount of thermal
energy equal to 112 500J is generated in the
brake drums. IF the mass of the brake
drums is 28 kg and their specific heat
capacity is 460.5 J/kg*k, what is the change
of temperature.
∆Q =mc∆T
∆T=∆Q /mc=112500/(28*460.5)
=8.70

Specific Heat Capacity - 2
Unit masses of different substances contain
• different numbers of molecules
• of different types
• of different masses
If the same amount of internal energy is
added to each unit mass
• it is distributed amongst the molecules

Specific Heat capacity - 3
The average energy change of each
molecule will be different for each
substance
Therefore the temperature changes will
be different
So the specific heat capacities will be
different

Thermal Equilibrium
When a cold body and a hot body are
placed in contact, thermal energy flows
from the hot body to the cold body until the
two temperatures are the same.
This is called thermal equilibrium.
The energy lost by the hot object is equal to
the energy gained by the cold object

Example 2
A piece of iron of mass 200g and temp. 3000
C is dropped into 1kg of water of temp. 200
C. What will be the temperature of the
water become? ciron= 470J/kg*K,
cwater=4200J/kg*k
mici(300-t)=mwcw(t-20)
T=260
C

Phases (States) of Matter
Matter is defined as anything that has
mass and occupies space
There are 4 states of matter
Solids, Liquids, Gases and Plasmas
Most of the matter on the Earth in the
form of the first 3
Most of the matter in the Universe is in
the plasma state

Change of State
Ordinary matter can exist as a solid, a
liquid, or a gas
Heating ice will turn it into water and
heating water will turn it into steam
In order for a piece of ice to melt it must be
0o
C and in order to turn water into steam it
must be 100o
C

Change of State
Once at the melting point, any additional
thermal energy supplied does not increase
the temperature.
The thermal energy is used rather to
overcome the forces between the water
molecules in the ice
The temperature of a substance will not
change until it completely changes its state

Latent Heat
The thermal energy which a particle
absorbs in melting, vaporising or
sublimation or gives out in freezing,
condensing or sublimating is called
Latent Heat because it does not
produce a change in temperature

Specific Latent Heat
Specific latent heat of fusion- Lf – is the
thermal energy required to melt a unit of
mass of material
Specific latent heat of vaporization- Lv – the
thermal energy required to vaporize a unit
mass at its boiling point

Specific Latent Heat
The term specific specifies that the thermal
energy necessary to change the phase of a
substance irrespective of mass

Specific Heat
The energy required to produce a phase
change is equal to the mass of the substance
as well as the latent heat of
fusion/vaporization.
Q = mLf
Q = mLv

Example 1
An ice cub of mas 25.0 g and temperature
-10 C is dropped into a glass of water of
mass 300.0 g and temperature 20 C. What is
the temperature eventually? (Specific heat
capacity of ice = 2200J/kg*k; Latent heat of
fusion of ice = 334 kj/kg)
11.9 C

Example 2
Thermal energy is provided at a constant
rate of 833J/s to 1kg of copper at the
melting temperature. If it takes 4 minutes to
completely melt the copper, find the latent
heat of fusion of copper.
Lf= 200 kJ/kg

Measuring Specific Heats
The specific heat capacity of a solid or
liquid can be measured by using an
electrical method that directly measures
energy flow into the body
Using a calorimeter and a heating element
you can connect the heating element to a
potential difference with a recorded voltage

Electrical Current
Current switched on at time t=0.
Q=V*I*t
I is current, V is voltage and t is time.
The energy absorbed by the substance and
the calorimeter is
Q= mc(Tmax-T)+C(Tmax-T)

Method of Mixtures
Have a substance of known mass, ms,
temperature, tsiand specific heat cs in a
calorimeter of temperature, tciand specific
heat Cc. To find the specific heat of an
unknown substance with known
temperature tiand mass m.
m*c*(ti-tf)=mscs(tf-tsi)+Cc(tf-ti)

Measuring specific latent heats
To measure specific latent heat such as ice
• Measure the mass of a quantity of ice
• Put the ice in water that is a few degrees above
room temperature
• Put the ice into the water and wait until it
reaches equilibrium
• The energy lost by the water and calorimeter is
the energy used to melt the ice and heat it up

Example
Suppose 25g of ice at 0 C is placed in an
aluminum calorimeter of mas 250 g (c=910)
containing 300g (c=4198) of water at 24 C.
The temperature of the water equilibrates at
17 C. Find the latent heat of fusion.
L=340kJ/kg

Evaporation
Molecules in a gas and liquid move about
with a distribution of speeds
If the most energetic particles are at the top
of the liquid they may escape the liquid
• This is known as evaporation
• Different from boiling
Since molecules are escaping the overall
kinetic energy of the liquid is decreased
• A reduced temperature of the liquid

Vapor Pressure
If the liquid is in an enclosed space, the
particles that evaporate collect above the
liquid in what is called vapor
As the liquid evaporates, the vapor pressure
increases
When the number of particles escaping the
liquid equals the number of particles falling
back into the liquid, the system has reached
equilibrium.

Kinetic Theory of Gases
1. A gas consists of a large number of molecules
2. Molecules move with a range of speeds
3. The volume of the molecules is negligible compared
with the volume of the gas itself
4. The collisions of the molecules with each other and the
container walls are elastic
5. Molecules exert no forces on each other or the container
except when in contact
6. The duration of the collisions is very small compared
with the time between collisions
7. The molecules obey Newton’s laws of mechanics.

Boltzmann Equation
Boltzmann Equation
• The average kinetic energy of the particles is
proportional to the absolute temperature of a
gas.
• v is the square root of the average of the squares of
the speed of the molecules of the gas
• If v we found the average of the speeds, it would equal 0.
• v is called the root mean square speed (rms speed)
• kB-Boltzmann Constant
• k=1.38x10-23
J/K

Example 6
Four molecules have speed 300m/s, 350m/s,
380m/s and 500m/s. Find the average speed
and the root mean square.
average= 382.5m/s
Rms speed= 389.5m/s
It is important to note the rms speed is not
exactly the average speed but a close/usable
approximation

Example 7
If the root mean square molecular speed is
doubled, what is the new temperature?
4x as large

Molecular explanation of
Pressure
Pressure is the normal force per unit area.
The pressure in a gas results from the
collisions of the gas molecules with the
walls of its container (and not from the
collisions between the molecules)

Molecular explanation of
Pressure
What two factors would affect the pressure
of a gas?
• The speed of the particles
• High kinetic energy means a greater force is applied
to the walls when the come in contact with the
molecules (temperature)
• The frequency of collisions
• More collisions means more chances that the wall
will get hit with a particle

Example 8
A gas is compressed slowly by a piston.
Explain why the temperature of the gas will
stay the same?
If gas is compressed slowly by a piston then
the speeds of the particles before and after
the collision of the piston’s wall will be
roughly equal. Since the average kinetic
energy of the particles would remain
roughly equal so would temperature.

Example 9
A gas is compressed rapidly by a piston.
Explain why the temperature of the gas will
increase.
The molecules rebounding off the rapidly
moving piston wall will be rebounded with
greater speed. The greater speed of the
molecules creates a larger kinetic energy
and thus a larger temperature.

Example 10
A gas expands isothermally (temp. is
constant). Explain why the pressure
decreases.
The volume of the gas expands, which
means that, on average, molecules have a
larger distance to travel between successive
collisions with the walls. Thus, the
collisions are less frequent than before and
so the pressure decreases.

Example 11
A gas is heated at a constant pressure.
Explain why the volume must increase as
well.
The temperature increases and so the molecules
move faster, on average. An increase in
temperature means the frequency of collisions
must drop in order to keep pressure constant. In
order for this to happen, the volume must expand
to increase distance between collisions.

Pressure
Pressure is defined as the normal force to an
area per unit area.
P=F/A
SI unit
• N/m2
-Pa pascal
Atmospheric Pressure
• 1atm=1.013x105
Pa

Example 1
Two hollow cubes of side 0.25cm with one
face missing are placed together at the
missing face. The air inside the solid
formed is pumped out. What force is
necessary to separate the cubes?
6.33x103
N

Gases
It is more useful to talk about the number of
moles of gas rather than the mass of the gas
itself.
NA= 6.02x1023
molecules/mole
n=N/NA
• n is the number of moles
• N is the number of molecules in a gas
From this we can related P, V, n, and T.

Example 2
How many molecules are there in 6 g of
hydrogen gas?
1.81x1024

Example 3
Make a rough estimate of the number of
water molecules in an ordinary glass of
water. (.3L)
1025
molecules

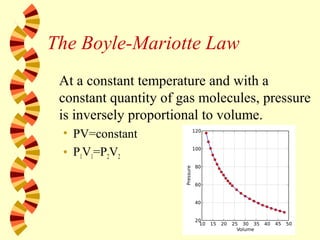
The Boyle-Mariotte Law
At a constant temperature and with a
constant quantity of gas molecules, pressure
is inversely proportional to volume.
• PV=constant
• P1V1=P2V2

Example 4
The pressure of a gas is 2 atm and its
volume 0.9L. If the pressure is increased to
6 atm at constant temperature, what is the
new volume?
0.3L

The volume Temperature Law
When the temperature is expressed in
kelvin, and pressure is held constant
• V/T=Constant
• V1/T1=V2/T2

Example 5
A gas expands at constant pressure from an
original volume of 2L at 22o
C to a volume
of 4L. What is the new temperature?
590K or 317o
C

Pressure Temperature Law
At a constant volume, pressure and
temperature are proportional.
• P/T= Constant
P1/T1=P2/T2

Example 6
A gas in a container of fixed volume is
heated from a temperature of 20o
C and
pressure 3 atm to a temperature of 85o
C.
What is the new pressure?
3.67atm

The Equation of State
If we recombine the results of the previous
law’s we find that
• PV/T=constant
Microscopically we found
• PV/T=n*Constant
• We found that all gases follow these rules so
• PV/nT=Constant
• Constant is R=8.31 J/K*mole
• PV=nRT

Example 7
How many moles of gas are there in a gas
of temperature 300K, volume 0.02m3
and
pressure 2x105
Pa?
1.60moles

Example 8
A container of hydrogen of volume 0.1m3
and temperature of 25o
C contains 3.20x1023
molecules. What is the pressure in the
container?
1.3x104
Pa

Example 9
A gas of volume 2L, pressure 3 atm and
temperature 300k expands to a volume of
3L and a pressure of 4 atm. What is the new
temperature of the gas?
600k

Example 10
The graph below shows three isothermal
curves for the same quantity of gas. Which
is a the highest temperature.
T1

Internal Energy
Chapter 3.1 defined the internal energy of a
gas as the total kinetic energy of the
molecules of the gas plus the potential
energy associated with intermolecular
forces
Ideal gas the intermolecular forces are 0

Internal Energy
Ek=
kB=R/NA=1.38x10-23
J/K Boltzmann
Constant
The Boltzmann constant is the value of the
gas constant of an idea gas per molecule.
The internal energy of a system can then be
given by
U=3/2NkT

Systems
Systems are the complete set of objects that
we are taking into consideration
• Systems can be as large such as planet earth of
the universe or small such as a cell or an atom.
An closed system does not allow mass to
enter or leave
An isolated system does not allow energy to
leave the system

Work done on or by a gas
If a gas is exerting a certain pressure on an
area of a piston and the piston moves
distance x the work done is equal to
• W=PAx
• Where A*x represents a
change in volume
• W=PdV

Note that as the volume changes the
pressure will also change.
Thus calculus would be needed and an
integral would be needed

The total work done when the gas expands
by an arbitrary amount is the area under the
graph in the pressure-volume diagram

Figure 4.4 shows an arbitrary series of
changes on an idea gas that begin and end
in state A.
The net work done is the
work done by the gas
minus the work done on
the gas (Figure 4.4c)

Many processes can be identified on a
pressure-volume diagram
Isobaric- Pressure
Isochoric-Volume
Isothermal-Temp
Adiabatic-Energy

Example 1
A gas is compressed at constant pressure
2.00x105
Pa from a volume of 2.00m3
to a
volume of 0.500m3
. What is the work done?
If the temperature initially was 40o
C what is
the final temperature of the gas?
3.00x105
J
-195O
C

Adiabatic vs Isothermal process
Isothermal process means that the
temperature of the gas is held constant
• Changing the volume can change pressure and
temperature
• Isothermal keeps a constant temperature
therefore constant internal energy ΔU=0
• Typically slow volume change or object is in
equilibrium with its environment
• Heat/cool reservoir

Adiabatic vs Isothermal process
Adiabatic means that there is no thermal
energy given off or absorbed by the system.
• Q=0
• Typically well insulated
• Fast reactions
• Temperature of gas is able to change but no
thermal energy can be added or subtracted
ΔQ=0

The first law of Thermodynamics
The change of internal energy of a system is
equal to the heat supplied to the system
minus the work done by the system on it’s
surroundings.
ΔU=Q-W
U=Internal energy
Q=Exchange of Heat
W=Work

Example 2
A gas in a container with a piston expands
isothermally (ie: the temperature stays
constant). If thermal energy Q=105
J is given
to the gas, what is the work done by the
gas?
105
J

Example 3
A gas expands adiabatically (ie. It does not
receive or lose thermal energy). Will it’s
temperature increase or decrease.
Decrease

Question 4
An ideal gas, kept at constant pressure
3.00x106
Pa, has initial volume 0.100m3
and
temperature 300k. If the gas is compressed
at constant pressure done to a volume of
0.080m3
, find:
• A) the work done on the gas;
• B) the thermal energy taken out of the gas
• A)6.00x104
J
• B) -1.5x105
J

Question 5
Figure 4.8 is a pressure-volume diagram
showing two adiabatic, an isochoric and an
isobaric process making up a loop ABCD
for an idea gas.
A)Along which legs is thermal energy
supplied or removed from the gas.
B) What is the relation between Qin, Qout
and the work done?
A) AB, CD B)W=Qin-Qout

The Second Law of
Thermodynamics
There are a many processes in
thermodynamics that are consistent with the
first law but are virtually impossible
• The spontaneous flow of thermal energy from a cold
body to a hotter body
• The air in a room suddenly occupying just one half of
the room and leaving the other half empty
• A glass of water at room temperature suddenly
freezing, causing the temperature of the room to rise.

The Second Law of
Thermodynamics
These processes do not happen because
they are forbidden by a very special law of
physics- The second law of
thermodynamics
The second law of thermodynamics deals
with the limitations imposed on heat
engines, devices whose aim is to convert
thermal energy (disordered energy) into
mechanical energy (ordered energy)

Entropy
Entropy, S, is a measure of “disorder”
• A measure of the number of ways a system can be
rearranged
The entropy of a system is not important but
rather the change of entropy is
important/calculable
ΔS=ΔQ/T
• S=entropy
• Q=thermal energy supplied
• T= temperature of system

The second law of
Thermodynamics
During a thermodynamic process the sum of
the entropies of the participating systems
must increase
The entropy of an isolated system never
decreases
It is impossible for thermal energy to
spontaneously flow from a cold to a hot
object

Degradation of Energy
It is a consequence of the second law that
energy, while always being conserved,
becomes less useful
• It goes from ordered energy to disordered
This is called energy degradation

3.2

More Related Content

What's hot (20)

Viewers also liked (16)

Similar to 3.2 (20)

Recently uploaded (20)

3.2