![Example
1. Expression y =
√
1 − x2 does not define a function on R,
but it defines a function on [−1, 1].
2. Expression y = ±
√
1 − x2 specifies coordinates of points of a unit circle,
however it does not define a function on [−1, 1].](https://image.slidesharecdn.com/5-171106232056/85/5-1-Defining-and-visualizing-functions-A-handout-16-320.jpg)
5.1 Defining and visualizing functions. A handout.
- 1. Introduction to set theory and to methodology and philosophy of mathematics and computer programming Defining and visualizing functions An overview by Jan Plaza c 2017 Jan Plaza Use under the Creative Commons Attribution 4.0 International License Version of November 4, 2017
- 2. Existence and uniqueness; Functions How to express in first-order logic “there exists unique y s.t. A(y)” without using the abbreviation ∃!y A(y) ? Existence: ∃y A(y). Uniqueness: ∀y1,y2 (A(y1) ∧ A(y2) → y1 =y2). Definition A function is any binary relation f such that ∀x ∀y1,y2 (xfy1 ∧ xfy2 → y1 =y2), or equivalently, ∀x (∃y xfy → ∀y1,y2 (xfy1 ∧ xfy2 → y1 =y2)). This means: if there is y s.t. xfy then such a y is unique. Definition. Let f be a function. 1. Let x ∈ domain(f). The value of f at x , f(x) , is the unique y such that xfy. 2. f maps x to y , denoted f : x → y or x f → y , if xfy.
- 3. x Is this a function? Yes.
- 4. x Is this a function? Yes.
- 5. x Is this a function? No. More than one value of y is paired with the same value of x.
- 7. Are these functions? { −1, 1 , 0, 0 , 1, 1 }, i.e. x y −1 1 0 0 1 1 Yes. { 1, 0 , 0, 1 , 1, 2 }, i.e. x y 1 0 0 1 1 2 No.
- 8. Are these functions? -1 0 1 -1 0 1 x Yes. 0 1 2 0 1 x No.
- 10. Are these functions? 0 -1 1 Yes. 0 1 2 No.
- 11. Terminology: total/partial, on Definition. Let f be a function. f is on X or f is a (total) function on X if domain(f) = X. Definition. f is a partial function on X if there is X ⊆X s.t. f is a function onX . Fact. If f is a partial function on X, then f is a total function on domain(f). If f is a function and X ⊇ domain(f), then f is a partial function on X. Fact. Consider these conditions: 1. f is a binary relation, 2. domain(f) ⊆ X, 3. for every x ∈ X, f maps x to at most one value, 4. for every x ∈ X, f maps x to least one value. Then: f is a function on X iff f satisfies conditions 1-4; f is a partial function on X iff f satisfies conditions 1-3.
- 12. Vertical line tests on the Cartesian plane are the following. Let G be a subset of the Cartesian plane. G is the graph of a function from R to R iff every straight line parallel to the y axis intersects G in exactly one point. G is the graph of a partial function from R to R iff every straight line parallel to the y axis intersects G in at most one point. Vertical line tests in discrete Cartesian diagrams are the following. Let G be a subset of X × Y in a discrete Cartesian diagram. G is the graph of a function from X to Y iff every column in the diagram contains exactly one point of G. G is the graph of a partial function from X to Y iff every column in the diagram contains at most one point of G.
- 13. Terminology: from, to Definition. Let f be a function. 1. f is to/into Y if range(f) ⊆ Y . 2. f is (a total function) from X to Y , denoted f : X −→ Y or X f −→ Y , if domain(f)=X and range(f) ⊆ Y . Definition f is a partial function from X to Y , denoted f : X −→ Y or X f −→ Y , if there exists X ⊆ X such that f : X −→ Y . f : X −→ Y f : X −→ Y domain(f) ⊆ X domain(f) = X range(f) ⊆ Y range(f) ⊆ Y Our definitions imply that the term “to/into Y ” applies to partial functions as well: for any partial function f, f is to/into Y iff range(f) ⊆ Y .
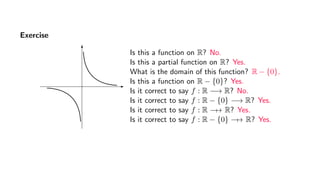
- 14. Exercise Is this a function on R? No. Is this a partial function on R? Yes. What is the domain of this function? R − {0}. Is this a function on R − {0}? Yes. Is it correct to say f : R −→ R? No. Is it correct to say f : R − {0} −→ R? Yes. Is it correct to say f : R −→ R? Yes. Is it correct to say f : R − {0} −→ R? Yes.
- 15. Example 1. Let f ={ 0, −1 , 1, 0 , 2, 3 }. f is a function from {0, 1, 2} to Z. f is also a function from {0, 1, 2} to {−1, 0, 3}. 2. Alternatively we could specify it as: a function f on {0, 1, 2} s.t. f(0)=−1, f(1)=0, f(2)=3. 3. Alternatively we could specify it as: a function f on {0, 1, 2} s.t. f : 0 → −1, f : 1 → 0, f : 2 → 3. 4. Alternatively we could specify it as: a function f on {0, 1, 2} s.t. f(x)=x2 − 1. 5. Let g be a function on {0, 1, 2, 3} s.t. g(x)=x2 − 1. Although g and f are defined by the same formula, they are different functions because they have different domains.
- 16. Example 1. Expression y = √ 1 − x2 does not define a function on R, but it defines a function on [−1, 1]. 2. Expression y = ± √ 1 − x2 specifies coordinates of points of a unit circle, however it does not define a function on [−1, 1].
- 17. Exercise Consider the formula y = √ x. (Recall that for x = 9 we have just y = 3, because the definition of square root requires it to be non-negative.) 1. Does this formula define a function from R to R? No. 2. Does this formula define a function from {u ∈ R : u 0} to R? Yes. 3. Does this formula define a partial function from R to R? Yes. 4. Does this formula define a function from {u ∈ R : u 0} to Q? No. 5. Does this formula define a function from {u ∈ R : u 0} to {u ∈ R : u 0}? Yes.
- 18. Exercise Are the following statements correct? 1. Let f1, f2 be functions. If domain(f1) = domain(f2) and f1 ⊆ f2, then f1 = f2. Yes. 2. Let R1, R2 be binary relations. If domain(R1) = domain(R2) and R1 ⊆ R2, then R1 = R2. No. 3. Let f1, f2 be partial functions on the same set X. If f1 ⊆ f2, then f1 = f2. No. Whenever the answer is negative, provide a counter-example.
- 19. Note 1. An attempt to define f : Q −→ Z: f(m n ) = m + n, where m, n ∈ Z. This is not correct, because 1 2 = 2 4 but f(1 2) = 1 + 2 = 3=6 = 2 + 4 = f(2 4) violating ∀x,y1,y2 (xfy1 ∧ xfy2 → y1 =y2). 2. An attempt to define g : Q −→ Z: let g(0)=1 and let g(m n ) = m + n where m, n ∈ Z, m=0, n > 0, and m and n do not have a common divisor greater than 1. This is correct. (We have used a canonical form of rational numbers.) 3. Every rational number has many representations (1 2 = 2 4 = ...). To be correct, the definition must be independent of the representation .
- 20. Exercise Let Q+ be the set of all positive rational numbers. Are these attempts to define a function correct? 1. f : Q −→ Q s.t. f(m n ) = n m where m, n ∈ Z. No. 2. f : Q+ −→ Q+ s.t. f(m n ) = n m where m, n ∈ Z. Yes. Show this by proving: if m1, n1, m2, n2 ∈ Z and m1 n1 , m2 n2 ∈ Q+ and m1 n1 = m2 n2 then n1 m1 = n2 m2 .
- 21. Note. An attempt to to model the concept “mother of”: 1. Persons is a non-empty set, 2. Persons is a finite set, 3. motherOf : Persons −→ Persons (i.e. every person has a unique mother, who is a person), 4. motherOf is a function such that for every p in its domain: p=motherOf(p), p=motherOf(motherOf(p)), p=motherOf(motherOf(motherOf(p))), etc. (i.e. there are no cycles). These conditions are contradictory. (The same problem occurs with theSupervisorOf in employee databases.) To see why, try drawing directed graphs showing a function motherOf on a three-element set Persons.