7 logaritmos

LOGARITMOS TRABAJO #7
1. Si log 𝑘 = 𝑥, entonces
log 100𝑘 =
A. 100+K B.100+x C. 2+K D. 2+X E. 2X
2. Si 𝑙𝑜𝑔√ 𝑥 = 0,3495, entonces log 𝑥2
=
A. 0,3495 B. (0,3495)2
C. 2 ∙ 0,3495 D. 4∙ 0,3495 E.4,3495
3. Si 𝑙𝑜𝑔𝑥 = 𝑎 𝑦
log 𝑦 = 𝑏, entonces log √ 𝑥𝑦 =3
A. 3𝑎 + 3𝑏 B. 3𝑎𝑏 C.
1
3
𝑎 +
1
3
𝑏 D.
1
3
𝑎 ∙ 𝑏 E. √ 𝑎 + b
3
4. Si log 𝑥 = 𝑎, 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠 𝑙𝑜𝑔 √ 𝑥 =
𝑨. 𝑎 𝑩. 2𝑎 𝑪.
1
2
𝑎 𝑫.√ 𝑎 𝑬. 𝑎
−
1
2
5. Si 𝑙𝑜𝑔𝑥 = 𝑦, 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠
𝑙𝑜𝑔10𝑥3
=
𝑨. 1 + 3𝑋 𝑩 .1 + 3y 𝐂. 10+ 3x 𝐃. 10 + 3Y 𝐄. 30Y
𝟔. Si 𝑒 𝑦
= 3,entonces y =
𝑨. log3 𝑩. 𝑙𝑛 3 𝑪. 𝑙𝑜𝑔3 − 𝑙𝑜𝑔 𝑒 𝑫. 𝑙𝑛3 − ln 𝑒 𝑬.
𝑙𝑛3
𝑒

𝟕. log√3 27 =
𝑨 .1 𝑩. 3 𝑪. 6 𝑫. 9 𝑬. 12
8. log81 9 =
𝑨. 2 𝑩. 1 𝑪 .
1
2
𝑫. −
1
2
𝑬.−1
9. log27
1
3
=
𝑨. 3 𝑩.1 𝑪.
1
3
𝑫.−
1
3
𝑬.−1
10. 𝑙𝑜𝑔
1
𝑥
+ 𝑙𝑜𝑔 𝑥 =
𝑨.
1
𝑋
log 𝑋 𝑩.log 𝑋 𝑪.−1 𝑫.0 𝑬.1
11. El valor de
log 𝑞 𝑝 ∙ log 𝑃 𝑟 ∙ log 𝑟 𝑞 𝑒𝑠 ∶

𝑨. 𝑝𝑞𝑟 𝑩.
1
𝑝𝑞𝑟
𝑪. 𝑝 + q + r 𝐃. 1 𝐄. 0
12. 𝐿𝑎 𝑒𝑥𝑝𝑟𝑒𝑠𝑖𝑜𝑛 𝑑𝑒 log 𝑎 𝑏 ∙ log 𝑏 𝑐 es equivalente a:
𝑨. log 𝑏 𝐶 𝑩.log 𝑐 𝑏 𝑪. log 𝑎 𝐶 𝑫.log 𝑎 𝑏𝑐 𝑬.log 𝑏 𝑎𝑐
13. La expresión log
𝑎
𝑏2 𝑐
es equivalente a:
𝑨. log 𝑎 − 2log 𝑏 + log 𝑐 𝑩.log 𝑎 − 2log 𝑏 + 2log 𝑐 𝑪. log 𝑎 − 2 log 𝑏 − log 𝑐
𝑫. log 𝑎 − 2 log 𝑏 − 2log 𝑐 𝑬.log 𝑎 + 2 log 𝑏 + log 𝑐
14. Si log 𝑥2
𝑦 = 𝑎
Y log
𝑥
𝑦2 = 𝑏, entonces log 𝑦 =
𝑨.
1
3
( 𝑎 − 2𝑏) 𝑩.
1
5
(2𝑎 + b) 𝑪.
1
3
( 𝑎 + 2b) 𝑫.
1
5
(2𝑎 − 𝑏) 𝑬.
1
5
(𝒂 − 𝟐𝒃)
15. Si log 𝑥 + log3 =
log60 − log20, 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠 𝑥 =
𝑨. 0 𝑩. 1 𝑪. 3 𝑫. 10 𝑬. 33

16. Si log 𝑛 − log 𝑥 =
2log 𝑦 − 1, 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠 𝑛 =
𝑨.
𝑥2 𝑦
10
B.
𝑥𝑦2
10
𝑪. 10𝑥2
𝑦 𝑫. 10𝑥𝑦2
𝑬. 𝑥(𝑦 − 1)2
17. Si 𝑝 𝑥−2
= 𝑞 𝑥+1
, entonces x =
𝑨. 2log 𝑝 𝑩. 2log 𝑝 + log 𝑞 𝑪.2log 𝑝 − log 𝑞 𝑫.
2 log 𝑝 + log 𝑞
log 𝑝 − log 𝑞
𝑩.
2 log𝑝 + log 𝑞
log 𝑞 − log 𝑝
18. 𝑆𝑖 𝑦 = 𝑎log 𝑎 𝑥
, 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠 𝑥 𝑣𝑎𝑙𝑒:
𝑨. log 𝑎 𝑦 𝑩. log 𝑦 𝑎 𝑪. 𝑦 𝑫. 0 𝑬. 1
19. La expresión
𝑎2log 𝑎 𝑥
∙ 𝑎log 𝑎 𝑦
= 1 𝑒𝑠 𝑒𝑞𝑢𝑖𝑣𝑎𝑙𝑒𝑛𝑡𝑒 𝑎:
𝑨. 2log 𝑎 𝑥 + log 𝑎
𝑦 = 0 𝑩. 2log 𝑎
𝑥 ∙ log 𝑎
𝑦 = 0 𝑪. 2 log 𝑎 𝑥 ∙ log 𝑎 𝑦 = 1
𝑫. 2 log 𝑎 𝑥 + log 𝑎
𝑦 = 1 𝑬. 𝑦 = 𝑥2
20. De las siguientes expresiones; son equivalentes:

I. 𝑏log 𝑏 𝑥
∙ 𝑏2 log 𝑏 𝑦= 𝑏log 𝑏1
II. log 𝑏 𝑥 + log 𝑏 𝑦2
= 0
III. 𝑥𝑦2
= 1
𝑨. 𝑠𝑜𝑙𝑜 𝐼 𝑦 𝐼𝐼 𝑩. 𝑠𝑜𝑙𝑜 𝐼𝐼 𝑦 𝐼𝐼𝐼 𝑪. 𝑠𝑜𝑙𝑜 𝐼 𝑦 𝐼𝐼𝐼 𝑫. 𝑇𝑜𝑑𝑎𝑠 𝑬. 𝑁𝑖𝑛𝑔𝑢𝑛𝑎
21. La expresión
5 log 𝑎 𝑎 − log 𝑎 𝑎4
+ log 𝑎 𝑎−2
vale:
𝑨. −2 𝑩.−1 𝑪. 0 𝑫.1 𝑬. 2
22. La expresión: log 𝑎 5 + log
1
𝑎
5 𝑣𝑎𝑙𝑒
𝑨. −2 𝑩.−1 𝑪. 0 𝑫. 1 𝑬. 1
23. El valor de log3 8 + log3
1
8
es igual a:
A. -2 B. -1 C. 0 D.1 E. 2
24. La expresión log2
1
3
+ log3
1
2
𝑒𝑠:
𝑨. log2 3 − log3 2 𝑩.−log2 3 − log3 2 𝑪.−log2 3 + log3 2
D. log2 3 + log3 2 E. −log2 5

25. Si 2x−2
+ 2x+2
= 17, entonces x vale:
𝑨. 2 𝑩. 1 𝑪. 0 𝑫.−1 𝑬.−2
26. Si 31−𝑥
− 3 𝑥−1
= 8 ∙ 3−1
, entonces x vale:
𝑨. 2 𝑩. 1 𝑪. 0 𝑫.−1 𝑬.−2
27. Si log( 𝑥 + 3) − log( 𝑥 + 2) = log 2, 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠 𝑥 𝑣𝑎𝑙𝑒
𝑨. 2 𝑩.1 𝑪. 0 𝑫.−1 𝑬.−2
28. En la expresión log3 𝑥 = 𝑝 + q, x vale:
𝑨. 3 𝑝
+ q 𝑩.3 𝑞
+ 𝑝 𝑪.3 𝑝+q
𝑫. 3 𝑝−𝑞
𝑬.3 𝑝
+ 3 𝑞
29. Si ln 𝑦 = ln 𝑦𝑜 − 𝑡, 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠 𝑦 𝑣𝑎𝑙𝑒:
𝑨. 𝑒−𝑡
∙ 𝑦0 𝑩. 𝑒−𝑡
− 𝑦0 𝑪. 𝑒−𝑡+𝑦0 𝑫. 𝑒−𝑡−𝑦0 𝑬. 𝒆 𝒕+𝑦0
30. Si
log 𝑥
2
=
2𝑙𝑜𝑔𝑦
3
, entonces:
𝑨. 𝑥3
− 𝑦4
= 0 𝑩. 𝑥3
+ 𝑦4
= 0 𝑪. 3𝑥 − 4𝑦 = 0 𝑫.3𝑥 + 4𝑦 = 0 𝑬. 𝑥 = √ 𝒚𝟑

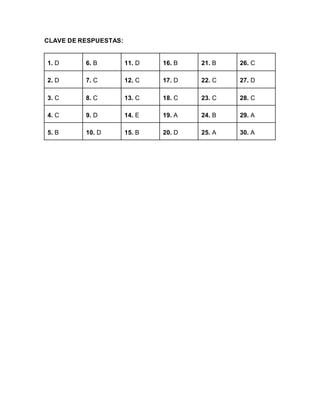
CLAVE DE RESPUESTAS:
1. D 6. B 11. D 16. B 21. B 26. C
2. D 7. C 12. C 17. D 22. C 27. D
3. C 8. C 13. C 18. C 23. C 28. C
4. C 9. D 14. E 19. A 24. B 29. A
5. B 10. D 15. B 20. D 25. A 30. A

7 logaritmos

More Related Content

What's hot (20)

More from Cris Panchi (20)

Recently uploaded (9)

7 logaritmos