第8回スキル養成講座講義資料.pdf
- 2. 前回のアンケート結果について • 高校生の方が圧倒的多数. 大学生の方ももちろんいますし, 対象です. • 興味は持っていただけたけれど, 内容を難しく感じた方が多かった. • 質問は, どの程度答えられるかは別として, してはいけないということはあ りませんので, 遠慮なくどうぞ. • 質問: 高校の内容の復習におすすめの教材は? →高校の教科書. 高校数学の 教材は充実しているので, 書店や図書館で相性の良いものを選べばOK. 2
- 3. 3回のプランの変更 1. イントロと準備 2. 主成分分析の考え方と線形代数. 3. 主成分分析の方法. 1. イントロと準備 2. 復習と3回への導入. 3. 主成分分析の考え方と線形代数. 変 更 アンケート結果に鑑みて, 講義の内容を以下のように変更します. 3
- 4. 参考書籍 • 応用がみえる線形代数 高松 瑞代 著 (岩波) • 線形代数の入門から応用までをわかりやすく 扱っている教科書. • 本講座では「テキスト」といったらこの本. • この講座では, 6の解説を目標とする. 4
- 5. 目標と内容の整理 • 都市の比較分析という課題に, 主成分分析を用いる. • 線形代数の入門として, 行列やベクトル, その演算について学ぶ. • 計算と具体的な課題への応用を通じて, 線形代数とその応用へ入門する. 5
- 6. 今日の目標と進め方 • 基本的には, 前回の復習. 少しだけ, 次回への接続. • 前半: 行列とベクトル, その計算について. 分散と共分散について. • 後半: 主成分分析に用いる, 標本分散共分散行列について. 6
- 8. 行列とベクトル 線形代数の登場人物 A x ベクトル 行列 縦横に並んだ数の組. 一列に並んだ数の組. 0 @ 1 2 0 1 0 0 4 2 0 0 1 0 0 1 2 1 A 例: 1行 2行 3行 1 列 2 列 3 列 4 列 5 列 例: 列ベクトル 行ベクトル 1 2 0 1 3 5行列と呼ぶ 4次元 0 @ 1 2 3 1 A 3次元 特 別 な 場 合 8
- 9. 行列の積 2つの行列に対して, その「積」が定義できる場合があります. (l m行列) (m n行列)=(l n行列) 0 B @ a11 · · · a1m . . . ... . . . a`1 · · · a`m 1 C A 0 B @ b11 · · · b1n . . . ... . . . bm1 · · · bmn 1 C A = 0 B @ c11 · · · c1n . . . ... . . . c`1 · · · c`n 1 C A cij = m X k=1 aikbkj = ai1b1j + ai2b2j + · · · + aimbmj 9 よこ たて
- 10. 行列の積 日常的な行列の積の具体例 飲料 おにぎり お菓子 新聞 雑誌 1人目の客 1 2 0 1 0 2人目の客 0 4 2 0 0 3人目の客 1 0 0 1 2 出典: 応用が見える線形代数(p.1) 金額ベクトル 0 @ 1 2 0 1 0 0 4 2 0 0 1 0 0 1 2 1 A 0 B B B B @ 100 120 90 110 350 1 C C C C A 飲料 おにぎり お菓子 新聞 雑誌 0 @ 1 2 0 1 0 0 4 2 0 0 1 0 0 1 2 1 A 0 B B B B @ 100 120 90 110 350 1 C C C C A = 0 @ 450 660 910 1 A 支払額ベクトル 1人目の客の支払額 2人目の客の支払額 3人目の客の支払額 購買情報行列 10
- 11. 前回の復習: 行列と変換 f : X ! Y ✓ a b c d ◆ ✓ a b c d ◆ ✓ x y ◆ = ✓ ax + by cx + dy ◆ 2 2行列の行列のベクトルへの積 0 0 は, 平面から平面への変換と見做せる(右図). 例. 回転 拡大/縮小 θ 0 0 0 ✓ cos ✓ sin ✓ sin ✓ cos ✓ ◆ ✓ 3 0 0 2 ◆ 対角行列 回転行列 11
- 12. 内積とノルム (行ベクトル) (列ベクトル)=(内積) y1 y2 · · · yn 0 B B B @ x1 x2 . . . xn 1 C C C A = n X k=1 xkyk = x1y1 + x2y2 + · · · + xnyn y = 0 B B B @ y1 y2 . . . yn 1 C C C A x = 0 B B B @ x1 x2 . . . xn 1 C C C A , y · x = t yx と表す. ノルム 0 n=2のとき, 高校で習うベクトルの内積と一致(右図). θ 2つのベクトル kxk = p x · x x, y に対して, y · x = kxkkyk cos ✓ が成り立つ. 12
- 13. 分散 nこのデータ(実数) に対して, その分散が, で定まる. 分散 平均 1 n n X i=1 (yi y)2 , y = 1 n n X i=1 yi 13 y1, y2, . . . , yn つまり…データの平均からのずれの度合いが分散 分散大 分散小
- 14. 共分散 2種類のnこのデータ(実数) と について, その共分散が y = 1 n n X j=1 yj z = 1 n n X k=1 zk , , で定義される. 平均 平均 共分散 つまり…二つのデータの「関係」を記述している (相関係数を定義するためにも用いられる). 14 y : y1, y2, . . . , yn z : z1, z2, . . . , zn 1 n n ∑ j=1 (yj − y)(zj − z)
- 15. 分散, 共分散と内積 分散は, ノルム を割ったもの 2 共分散は, 内積を割ったもの e y = 0 B B B @ y1 y y2 y . . . yn y 1 C C C A とすると, yの分散 2 (y) = 1 n ke yk2 e y = 0 B B B @ y1 y y2 y . . . yn y 1 C C C A e z = 0 B B B @ z1 z z2 z . . . zn z 1 C C C A , cov(y, z) = 1 n e y · e z とすると yとzの共分散 15
- 16. 標本分散共分散行列 で定義される行列. n個のm次元ベクトル に対して, その標本分散共分散行列とは, x1 = 0 B @ x11 . . . x1m 1 C A , · · · , xn = 0 B @ xn1 . . . xnm 1 C A S = 0 B @ s11 · · · s1m . . . ... . . . sm1 · · · smm 1 C A , skj = 1 n n X i=1 (xij xj)(xik xk), xj = 1 n n X i=1 xij S = 0 B @ s11 · · · s1m . . . ... . . . sm1 · · · smm 1 C A , skj = 1 n n X i=1 (xij xj)(xik xk), xj = 1 n n X i=1 xij 16 k=jのとき, 分散 k jのとき, 共分散 つまり… 分散と共分散を綺麗に並べた行列.
- 18. 前回の復習: 講座を通して考える問題 都市の比較分析 都市項目 生活の利便性 安心・安全 医療・介護 教育 都市1 6.0 2.7 2.1 6.5 都市2 6.7 2.2 2.5 6.4 都市3 5.9 3.0 1.9 6.5 都市4 6.6 5.0 2.4 6.8 都市5 7.0 2.6 2.5 6.0 都市6 8.1 4.2 4.5 6.3 都市7 7.2 2.8 2.5 6.2 都市8 7.0 3.1 2.5 5.9 都市9 7.2 2.5 2.1 5.4 都市10 5.6 2.2 1.8 4.5 都市1〜10に対して, 以下の4項目を10点満点で評価した結果, 以下の表のようになった. このデータから, 何を読み取れるか? 18
- 19. 考え方: このデータの「特徴」をよく表した新しい評価値を与える. : 都市 i の生活の利便性の評価値 evw(xi) = w1xi1 + w2xi2 + w3xi3 + w4xi4 evw(xi) = w1xi1 + w2xi2 + w3xi3 + w4xi4 vw(xi) = w1xi1 + w2xi2 + w3xi3 + w4xi4 w1xi1 + w2xi2 + w3xi3 + w4xi4 : 都市 i の 安心・安全 の評価値 : 都市 i の 医療・介護 の評価値 : 都市 i の 教育 の評価値 新しい評価値 各評価値に与える 重み(weight). evw(xi) = w1xi1 + w2xi2 + w3xi3 + w4xi4 前回の復習: 講座を通して考える問題 都市の比較分析 19
- 20. Q. どんな重みをつけた新しい評価値が, 「良い評価値」なのか? 主成分分析の考え方: 「結果に差が出る評価値」が良い評価値. 今回の評価は, 4項目もあるので, 比較が大変. → より結果の特徴を捉えた, 2つの評価値を選んで, 分析. 「分散」が大きい. 講座を通して考える問題 都市の比較分析 20
- 22. 問. 評価値の分散をどうすれば最大化できるか? 重さを与えたときに, その重さを使ってできた評価値の分散を返す関数 の最大値を求めよ. 重み 評価値 評価値の分散 ただし, この問題は, 重みの「総量」に制限をしないと意味をなさない. (この点については, 後でもう一度説明します) evw(xi) = w1xi1 + w2xi2 + w3xi3 + w4x w 2 (evw(x)) 22
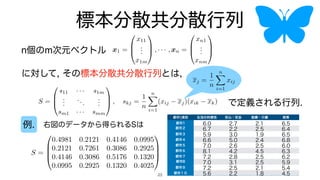
- 23. 標本分散共分散行列 で定義される行列. n個のm次元ベクトル に対して, その標本分散共分散行列とは, 例. x1 = 0 B @ x11 . . . x1m 1 C A , · · · , xn = 0 B @ xn1 . . . xnm 1 C A S = 0 B @ s11 · · · s1m . . . ... . . . sm1 · · · smm 1 C A , skj = 1 n n X i=1 (xij xj)(xik xk), xj = 1 n n X i=1 xij S = 0 B @ s11 · · · s1m . . . ... . . . sm1 · · · smm 1 C A , skj = 1 n n X i=1 (xij xj)(xik xk), xj = 1 n n X i=1 xij 都市項目 生活の利便性 安心・安全 医療・介護 教育 都市1 6.0 2.7 2.1 6.5 都市2 6.7 2.2 2.5 6.4 都市3 5.9 3.0 1.9 6.5 都市4 6.6 5.0 2.4 6.8 都市5 7.0 2.6 2.5 6.0 都市6 8.1 4.2 4.5 6.3 都市7 7.2 2.8 2.5 6.2 都市8 7.0 3.1 2.5 5.9 都市9 7.2 2.5 2.1 5.4 都市10 5.6 2.2 1.8 4.5 右図のデータから得られるSは S = 0 B B @ 0.4981 0.2121 0.4146 0.0995 0.2121 0.7261 0.3086 0.2925 0.4146 0.3086 0.5176 0.1320 0.0995 0.2925 0.1320 0.4025 1 C C A 23
- 24. 分散と標本分散共分散行列との関係 重みベクトル n個のm次元ベクトル x1 = 0 B @ x11 . . . x1m 1 C A , · · · , xn = 0 B @ xn1 . . . xnm 1 C A と w = 0 B @ w1 . . . wm 1 C A に対して, 評価値 の分散は, evw(xi) = t wxi = w1xi1 + · · · + wmxim S = 0 B @ s11 · · · s1m . . . ... . . . sm1 · · · smm 1 C A , skj = 1 n n X i=1 (xij xj)(xik xk), xj = 1 n n X i=1 標本分散共分散行列 を用いて, で与えられる. t wSw = m X j=1 m X k=1 wjwksjk 証明は, テキストの 6.3 24
- 25. 問. 評価値の分散をどうすれば最大化できるか? 重さを与えたときに, その重さを使ってできた評価値の分散を返す関数 の最大値を求めよ. 重み 評価値 評価値の分散 t wSw = m X j=1 X k evw(xi) = w1xi1 + w2xi2 + w3xi3 + w4x w 直接的な表示 2 (evw(x)) = ただし, この問題は, 重みの「総量」に制限をしないと意味をなさない. (この点について, 次のスライドで説明します) 25
- 26. 分散と重みベクトルについての観察. w0 = kw のとき, t w0 Sw0 = k2 (t wSw) 定数倍すれば, いくらでも分散を大きくできる. あくまで, 「ウェイト」をどう配分するかなので, その長さを固定する: kwk = 1. 問. という条件の下で, 分散 を最大にする ベクトル を求めよ. この を第一主成分と呼ぶ. kwk = 1. t w0 Sw0 = k2 (t wSw) kwk = 1. kwk = 1. 26
- 28. まとめと次回予告 • 分散・共分散は, データの特徴を表す量. • 分散・共分散を線形代数で見ると, ノルムや内積と思える. • 標本分散共分散行列は, データの分散と共分散を並べた行列. • 標本分散共分散行列を変換と思うと, 重みから定まる評価値の分散は, 重 みのベクトルとそれを変換したものの内積と思うことができる. • 次回は, この視点が実際に最大値を求める時にどう役立つかを学びます. 28