Advanced Computer Architecture
- 2. Subject: ADVANCED COMPUTER ARCHITECTURE Credits: 4 SYLLABUS Computer System Generation of computers, Classification of computers, Organization, Structure and function, Von Neumann architecture. System bus, Bus Structure, Elements of Bus design (Type, Arbitration, Timing, Width, Data transfer Type), Interrupts, Instruction Cycle state Diagram with interrupts/Without interrupts, Characteristic of Internal memory (ROM, PROM, EPROM, Flash memory), Input / Output: (External / Peripheral Device, Function of I/O module, Programmer I/O, Interrupt Driver I/O DMA) The Central Processing Unit ALU, Binary Arithmetic, Floating point Arithmetic, Basic combinational and sequential Circuit Design, RTL representation, Suggested Reading: John L. Hennessy and David A. Patterson. Computer Architecture: A Quantitative Approach (Third Edition ed.). Morgan Kaufmann Publishers. Laplante, Phillip A. (2001). Dictionary of Computer Science, Engineering, and Technology.
- 3. 2 Lecture 1 INTRODUCTION TO COMPUTERS Objectives of the lecture: 1. To understand the basics of the computer. Hello! Students, In today’s information age, computers are being used in every occupation. They are used by people of all age and profession, in their work as well as their leisure. This new social age have changed the basic concept of ‘Computing’. Computing, in today’s information age, is no more limited to computer programmers and computer engineers. Rather than knowing how to program a computer, most computer users simply need to understand how a computer functions so in this lecture I will be discussing with you about this versatile tool, why is it so powerful and useful, its history and you will also be briefed about the classification of computers its devices in my today’s lecture. What is A Computer? A computer is an electronic machine that accepts information, stores it until the information is needed, processes the information according to the instructions provided by the user, and finally returns the results to the user. The computer can store and manipulate large quantities of data at very high speed, but a computer cannot think. A computer makes decisions based on simple comparisons such as one number being larger than another. Although the computer can help solve a tremendous variety of problems, it is simply a machine. It cannot solve problems on its own. History of Computers Since civilizations began, many of the advances made by science and technology have depended upon the ability to process large amounts of data and perform complex mathematical calculations. For thousands of years, mathematicians, scientists and businessmen have searched for computing machines that could perform calculations and analyze data quickly and efficiently. One such device was the abacus. The abacus was an important counting machine in ancient Babylon, China, and throughout Europe where it was used until the late middle ages. It was followed by a series of improvements in mechanical counting machines that led up to the development of accurate mechanical adding machines in the 1930’s. These machines used a complicated assortment of gears and levers to perform the calculations but they were far to slow to be of much use to scientists. Also, a machine capable of making simple decisions such as which number is larger was needed. A machine capable of making decisions is called a computer.
- 4. 3 The first computer like machine was the Mark I developed by a team from IBM and Harvard University. It used mechanical telephone relays to store information and it processed data entered on punch cards. This machine was not a true computer since it could not make decisions. In June 1943, work began on the world's first electronic computer. It was built at the University of Pennsylvania as a secret military project during World War II and was to be used to calculate the trajectory of artillery shells. It covered 1500 square feet and weighed 30 tons. The project was not completed until 1946 but the effort was not wasted. In one of its first demonstrations, the computer solved a problem in 20 seconds that took a team of mathematicians three days. This machine was a vast improvement over the mechanical calculating machines of the past because it used vacuum tubes instead of relay switches. It contained over 17,000 of these tubes, which were the same type tubes used in radios at that time. The invention of the transistor made smaller and less expensive computers possible. Although computers shrank in size, they were still huge by today’s standards. Another innovation to computers in the 60’s was storing data on tape instead of punched cards. This gave computers the ability to store and retrieve data quickly and reliably. Classification of Computers ƒ Mainframe Computers ƒ Minicomputers ƒ Microcomputers ƒ Supercomputers Mainframe computers are very large, often filling an entire room. They can store enormous of information, can perform many tasks at the same time, can communicate with many users at the same time, and are very expensive. . The price of a mainframe computer frequently runs into the millions of dollars. Mainframe computers usually have many terminals connected to them. These terminals look like small computers but they are only devices used to send and receive information from the actual computer using wires. Terminals can be located in the same room with the mainframe computer, but they can also be in different rooms, buildings, or cities. Large businesses, government agencies, and universities usually use this type of computer. Minicomputers : are much smaller than mainframe computers and they are also much less expensive. The cost of these computers can vary from a few thousand dollars to several hundred thousand dollars. They possess most of the features found on mainframe computers, but on a more limited scale. They can still have many terminals, but not as many as the mainframes. They can store a tremendous amount of information, but again usually not as much as the mainframe. Medium and small businesses typically use these computers. Microcomputers : These computers are usually divided into desktop models and laptop models. They are terribly limited in what they can do when compared to the larger models discussed
- 5. 4 above because they can only be used by one person at a time, they are much slower than the larger computers, and they cannot store nearly as much information, but they are excellent when used in small businesses, homes, and school classrooms. These computers are inexpensive and easy to use. They have become an indispensable part of modern life. Computer Tasks ƒ Input ƒ Storage ƒ Processing ƒ Output When a computer is asked to do a job, it handles the task in a very special way. 1. It accepts the information from the user. This is called input. 2. It stored the information until it is ready for use. The computer has memory chips, which are designed to hold information until it is needed. 3. It processes the information. The computer has an electronic brain called the Central Processing Unit, which is responsible for processing all data and instructions given to the computer. 4. It then returns the processed information to the user. This is called output. Every computer has special parts to do each of the jobs listed above. Whether it is a multi- million dollar mainframe or a thousand dollar personal computer, it has the following four components, Input, Memory, Central Processing, and Output. The central processing unit is made up of many components, but two of them are worth mentioning at this point. These are the arithmetic and logic unit and the control unit. The control unit controls the electronic flow of information around the computer. The arithmetic and logic unit, ALU, is responsible for mathematical calculations and logical comparisons. Input Devices ƒ Keyboard ƒ Mouse ƒ Scanner ƒ Microphone ƒ CD-ROM ƒ Joystick
- 6. 5 Memory Read Only Memory (ROM) ROM is a small area of permanent memory that provides startup instructions when the computer is turned on. You can not store any data in ROM. The instructions in ROM are set by the manufacturer and cannot be changed by the user. The last instruction in ROM directs the computer to load the operating system. Every computer needs an operating system. This is a special computer program that must be loaded into memory as soon as the computer is turned on. Its purpose is to translate your instructions in English into Binary so that the computer can understand your instructions. The operating system also translates the results generated by your computer into English when it is finished so that we can understand and use the results. The operating system comes with a computer. Random Access Memory (RAM) This is the area of memory where data and program instructions are stored while the computer is in operation. This is temporary memory. NOTE: The data stored in RAM is lost forever when the power is turned off. For this reason it is very important that you save your work before turning off your computer. This is why we have peripheral storage devices like your computer’s hard disk and floppy diskettes. Permanent Memory (Auxiliary Storage) Your files are stored in permanent memory only when saved to your disk in a: drive or saved to your computer's hard disk, Drive c: To better understand how a computer handles information and to also understand why information is lost if the power goes off, let’s take a closer look at how a computer handles information. Your computer is made of millions of tiny electric circuits. For every circuit in a computer chip, there are two possibilities: 1. an electric circuit flows through the circuit or 2. An electric circuit does not flow through the circuit. When an electric current flows through a circuit, the circuit is on. When no electricity flows, the circuit is off. An “on” circuit is represented by the number one (1) and an off circuit is represented by the number zero (0). The two numbers 1 and 0 are called bits. The word bit comes from “binary digit”. Each time a computer reads an instruction, it translates that instruction into a series of bits, 1’s and 0’s. On most computers every character from the keyboard is translated into eight bits, a combination of eight 1’s and 0’s. Each group of eight bits is called a byte.
- 7. 6 Byte – The amount of space in memory or on a disk needed to store one character. 8 bits = 1 Byte Since computers can handle such large numbers of characters at one time, metric prefixes are combined with the word byte to give some common multiples you will encounter in computer literature. Kilo means 1000 kilobyte (KB) = 1000 Bytes Mega means 1,000,000 megabyte (MB) = 1,000,000 Bytes Giga Means 1,000,000,000 gigabyte (GB) = 1,000,000,000 Bytes At this point it would be good to point out why information stored in RAM is lost if the power goes off. Consider the way the following characters are translated into binary code for use by the computer. A 01000001 B 01000010 C 01000011 X 01011000 Z 01011010 1 00110001 2 00110010 Consider the column at the right, which represents how the computer stores information. Each of the 1’s in the second column represents a circuit that is “on”. If the power goes off, these circuits can NOT be “on” any more because the electricity has been turned off and any data represented by these circuits is lost Central Processing Unit (CPU) The central processing unit is one of the two most important components of your microcomputer. It is the electronic brain of your computer. In addition to processing data, it controls the function of all the other components. The most popular microprocessors in IBM compatible computers are made by Intel. The generations of microprocessors are listed below. 1981 8088 1984 80286 1987 80386 1990 80486 1993 Pentium 1996 P-1 2002 P-4
- 8. 7 Output Devices Monitor Speakers Printer Impact Daisy Wheel Dot Matrix Non-Impact Ink Jet Laser Storage Devices Floppy disk Tape drive Local drive (c) Network drive (z) CD-ROM Zip disk Telecommunications Telecommunications means that you are communicating over long distances usually using phone lines. This enables you to send data to and receive data from another computer that can be located down the street, in another town, or in another country. Telecommunications requires a communication device called a modem, which connects your computer to a standard phone jack. A modem converts the digital signals that your computer uses into analog signals that can be transmitted over the phone lines. To use a modem, you must also have communication software to handle the transmission process. Computer Software System Software System software will come provided with each computer and is necessary for the computer’s operation. This software acts as an interpreter between the computer and user. It interprets your instructions into binary code and likewise interprets binary code into language the user can understand. In the past you may have used MS-DOS or Microsoft Disk Operating System which was a command line interface. This form of system software required specific commands to be typed. Windows 95 is a more recent version of system software and is known as a graphical interface. This means that it uses graphics or "icons" to represent various operations. You no longer have to memorize commands; you simply point to an icon and click.
- 9. 8 Program Software Program software is software used to write computer programs in specific computer languages. Application Software Application software is any software used for specified applications such as: ƒ Word Processing ƒ Spreadsheet ƒ Database ƒ Presentation Graphics ƒ Communication ƒ Tutorials ƒ Entertainment, Games Emerging Trends The components of a computer are connected by using buses. A bus is a collection of wire that carry electronic signals from one component to another. There are standard buses such as Industry Standard Architecture (ISA), Extended Industry Standard Architecture (EISA), Micro- Channel Architecture (MCA), and so on. The standard bus permits the user to purchase the components from different vendors and connect them easily. The various input and output devices have a standard way of connecting to the CPU and Memory. These are called interface standards. Some popular interface standards are the RS-232C and Small Computer System Interconnect (SCSI). The places where the standard interfaces are provided are called ports. Data Representation Bits and Bytes Data in Computers are represented using only two symbols '0' & '1'. These are called "Binary digiTS" (or) "BITS" for short. A set of 8 bits is called a byte and each byte stores one character. 2n Unique strings are represented using n bits only. For example, Using 2 bits we can represent 4=(22 ) unique strings as 00, 01, 10, 11. ASCII (American Standards Code for Information Interchange) codes are used to represent each character. The ASCII code includes codes for English Letters (Both Capital & Small), decimal digits, 32 special characters and codes for a number of symbols used to control the operation of a computer which are non-printable. Binary numbers Binary numbers are formed using the positional notation. Powers of 2 are used as weights in the binary number system. A binary number system. A binary number 10111, has a decimal value
- 10. 9 equal to 1*24 +0*23 +1*21 +1*20 =23. A decimal number is converted into an equivalent binary number by dividing the number by 2 and storing the remainder as the least significant bit of the binary number. For example, consider the decimal number 23. Its equivalent binary number is obtained as show below in figure CONVERSION OF DECIMAL TO BINARY EXAMPLE. 23 = (0111)2 Hexadecimal Numbers High valued binary numbers will be represented by a long sequence of 0's and 1's. A more concise representation is using hexadecimal representation. The base of the hexadecimal system is 16 and the symbols used in this system are 0,1,2,4,5,6,7,8,9,A,B,C,D,E,F. Strings of 4 bits have an equivalent hexadecimal value. For example, 6B is represented by 0110 1011 or 110 1011, 3E1 is represented by 0011 1110 0001 or 11 1110 0001 and 5DBE34 is represented by 101 1101 1011 1110 0011 0100. Decimal fractions can also be converted to binary fractions. Parity Check Bit Errors may occur while recording and reading data and when data is transmitted from one unit to another unit in a computer Detection of a single error in the code for a character is possible by introducing an extra bit in its code. This bit, know as the parity check bit, is appended to the code. The user can set the parity bit either as even or odd. the user chooses this bit so that the total number of ones ('1') in the new code is even or odd depending upon the selection. If a single byte is incorrectly read or written or transmitted, then the error can be identified using the parity check bit. Input Devices Key Board The most common input device is the Keyboard. It is used to input letters, numbers, and commands from the user. Mouse Mouse is a small device held in hand and pushed along a flat surface. It can move the cursor in any direction. In a mouse a small ball is kept inside and the ball touches the pad through a hole at the bottom of the mouse. When the mouse is moved, the ball rolls. This movement of the ball is converted into electronic signals and sent to the computer. Mouse is very popular in the modern computers that use Windows and other Graphical User Interface (GUI) applications. Magnetic Ink Character Recognition (MICR) In this method, human readable characters are printed on documents such In this method, human readable characters are printed on documents such as cheque using special magnetic ink. The cheque can be read using a special input unit, which can recognize magnetic ink characters. This
- 11. 10 method eliminates the need to manually enter data from cheques into a floppy. Besides saving time, this method ensures accuracy of data entry and improves security. Optical Mark Reading and Recognition (OMR) In this method, special pre-printed forms are designed with boxes which can be marked with a dark pencil or ink. Such a document is read by a document reader, which transcribes the marks into electrical pulses which are transmitted to the computer. These documents are applicable in the areas where responses are one out of a small number of alternatives and the volume of data to be processed is large. For example: • Objective type answer papers in examinations in which large number of candidates appear. • Market surveys, population survey etc., • Order forms containing a small choice of items. • Time sheets of factory employees in which start and stop times may be marked. The advantage of this method is that information is entered at its source and no further transcription is required. Optical Character Recognition (OCR) An optical scanner is a device used to read an image, convert it into a set of 0's and 1's and store it in the computer's memory. The image may be hand-written document, a typed or a printed document or a picture. Bar Coding In this method, small bars of varying thickness and spacing are printed on packages, books, badges, tags etc., which are read by optical readers and converted to electrical pulses. The patterns of bars are unique an standardized. For example, each grocery product has been given unique 10-digit code and this is represented in bar code form on every container of this product. Speech Input Unit A unit, which takes spoken words as its input, and converts them to a form that can be understood by a computer is called a speech input unit. By understanding we mean that the unit can uniquely code (as a sequence of bits) each spoken word, interpret the word and initiate action based on the word.
- 12. 11 Output Devices Monitor or Video Display Unit (VDU) Monitors provide a visual display of data. It looks like a television. Monitors are of different types and have different display capabilities. These capabilities are determined by a special circuit called the Adapter card. Some popular adapter cards are, • Color Graphics Adapter (CGA) • Enhanced Graphics Adapter (EGA) • Video Graphics Array (VGA) • Super Video Graphics Array (SVGA) THE LECTURES IN A GO • Defination Of computer • History Of Computers • Classification Of Computers • Explanation about i/p and o/p devices • Explanation about storage devices • Types of computer software
- 13. 12 Questions: 1. When u switch on your computer which software you see first and what is the utility of that software. 2. Suppose on fine day you are working on ur computer and power goes off, again u switch on our computer, what type of booting is done by that computer. 3. Write the essential parts of ur computer system without which u cant work and also list that parts which are optional. 4. How many types of storage are normally there in storage unit of a computer system? Justify the need for each storage type. Explain them. 5. What are the basic components of the CPU of a computer systems ? Describe the roles of each of the components in the functioning of a computer systems. 6. Suppose an entrance exam is held and thousands of students appeared in that exam, Which device u will use to evaluate the answer sheets and why? 7. Hardware and software are like two sides of a coin. Do you agree or disagree, Give reasons. END OF TODAYS LECTURE… References: 1. COMPUTER FUNDAMENTALS Pradeep .K.Sinha and Priti Sinha , BPB PUBLICATIONS 2. COMPUTER ORGANISATION AND ARCHITECTURE William Stallings Prentice PUBLICATIONS
- 14. 13 Lecture 2 GENERATIONS OF COMPUTERS Objectives of the lecture: 1.To learn the generation of the computers. Hello!friends , I am sure now you must be well versed with the History of computers from the previous lecture .Today I will be completing the remaining part of the previous lecture and then starting with the generations which tells how it has evolved from its early days, to become a powerful and useful tool for all types of users in today’s society. So Lets start on.. Contd. Lets start with the defination of Pixels, the smallest dot that can be displayed is called a pixel. The number of pixels that can be displayed vertically and horizontally gives the maximum resolution of the monitor. The resolution of the monitor determines the quality of the display. The higher the resolution the better is the quality of the display. Some popular resolution are 800*640 pixels, 1024*768 pixels, 1280*1024 pixels. Printer Line printer • It prints a complete line at a time. • Printing speed varies from 150 lines to 2500 lines per minute with 96 to 160 character on a 15-inch line. • Six to eight lines per vertical inch are printed. • Usually 64 and 96 character sets are used with English letters. • Two types of Line Printers are available. • Drum Printers: It consists of a cylindrical drum. The characters to be printed are embossed on its surface • Chain Printers: I have a steel band on which the character sets are embossed. Serial Printers • It prints one character at a time, with the print head moving across a line. • They are similar to typewriters.
- 15. 14 • They are normally slow (30 to 300 character per second) • The most popular serial printer is "Dot Matrix Printer". • Her character to be printed is made up of a finite number of dots and so, the print head consists of an array of pins. • Characters to be printed are sent one character at a time from the memory to the printer. The character code is decoded by the printer electronics and activates the appropriate pins in the print head. • Many dot matrix printers are bi-directional. i.e. they print form left to right as well as from right to left on return. This enhances the speed of printing. • The printing speed is around 300 characters per second. Letter Quality Printers • Here the characters are represented by sharp continuous lines and so the output is good looking • An example of such a printer is "Inkjet Printer". • It consists of a print head, which has a number of small hole or nozzles. • Individual holes can be heated very rapidly by an integrated circuit resistor. When the resistor heats up, the ink near it vaporizes and is ejected through the nozzle and makes a dot on paper placed near the head. • A high-resolution inkjet printer has around 50 nozzles within a height of 7mm and can print with a resolution of 300 dots per inch. • Latest inkjet printers have multiple heads, on per color, which allows color printing. • The printing speed is around 120 characters per second. Laser Printers • Here an electronically controlled laser beam traces out the desired character to be printed on a photoconductive drum. The drum attracts an ink toner on o the exposed areas. This image is transferred to the paper, which comes in contact with the drum. • Low speed laser printers, which can print 4 to 16 pages per minute, are now very popular and the unit cost is around Rs.0.5 lakh. • Very fast printers print 10,000 lines per minute and cost per unit is around R.5 lakhs. These printers give excellent outputs and can print a variety of fonts. • As these printers do not have type head striking on a ribbon, they are known as non- impact printers.
- 16. 15 Apart from printers, the other output devices are given below: 1. Drum Plotter 2. Flat Bed Plotter 3. Microfilm and Microfiche 4. Graphic Display device (Digitizing Tablet) 5. Speech Output Unit Computer Memory Main Memory A flip-flop made of electronic semiconductor devices is used to fabricated a memory cell. These memory cells organized as a Random Access Memory (RAM). Each cell has a capability to store one bit of information. A main memory or store of a computer is organized using a large number of cells. Each cell stores a binary digit. A memory cell, which does not loose the bit stored in it when no power is supplied to the cell, is know as a non-volatile cell. A word is a group of bits, which are stored and retrieved as a unit. A memory system is organized to store a number of words. A Byte consists of 8 bits. A word may store one or more bytes. The storage capacity of a memory is the number of bytes it can store. The address of the location from where a word is to be retrieved or to be stored is entered in a Memory Address Register (MAR). The data retrieved from memory or to be stored in memory are placed in a Memory Data Register (MDR). The time taken to write a word is known as the Write time. The time to retrieve information is called the Access time of the memory. The time taken to access a word in a memory is independent of the address of the word and hence it is know as a Random Access Memory (RAM). The main memory used to store programs and data in a computer is a RAM. A RAM may be fabricated with permanently stored information, which cannot be erased. Such a memory is called a Read Only Memory (ROM). For more specialized uses, a user can store his won special functions or programs in a ROM. Such ROM's are called Programmable ROM (PROM). A serial access memory is organized by arranging memory cells in a linear sequence. Information is retrieved or stored in such a memory by using a read/write head. Data is presented serially for writing and is retrieved serially during read. Secondary or Auxiliary storage devices Magnetic surface recording devices commonly used in computers are Hard disks, Floppy disks, CD-ROMs and Magnetic tapes. These devices are known as secondary or auxiliary storage devices. We will see some of these devices below.
- 17. 16 Floppy Disk Drive (FDD) In this device, the medium used to record the data is called as floppy disk. It is a flexible circular disk of diameter 3.5 inches made of plastic coated with a magnetic material. This is housed in a square plastic jacket. Each floppy disk can store approximately on million characters. Data recorded on a floppy disk is read and stored in a computer's memory by a device called a floppy disk is read and stored in a computer's memory by a device called a floppy disk drive (FDD). A floppy disk is inserted in a slot of the FDD. The disk is rotated normally at 300 revolutions per minute. A reading head is positioned touching a track. A voltage is induced in a coil wound on the head when a magnetized spot moves below the head. The polarity of the induced voltage when a 0 is read. The voltage sensed by the head coil is amplified, converted to an appropriate signal and stored in computer's memory. • Floppy Disks com with various capacities as mentioned below. • 51/4 drive- 360KB, 1.2MB (1 KB= 210 = 1024 bytes) • 31/2 drive- 1.44 Mb, 2.88 MB (1MB= 220 bytes) Compact Disk Drive (CDD) CD-ROM (Compact Disk Read Only Memory) used a laser beam to record and read data along spiral tracks on a 51/4 disk. A disk can store around 650 MB of information. CD-ROMs are normally used to store massive text data. (such as encyclopedias) which is permanently recorded and read many times. Recently CD writers have come in the market. Using a CD writer, lot of information can be written on CD-ROM and stored for future reference. Hard Disk Drive (HDD) Unlike a floppy disk that is flexible and removable, the hard disk used in the PC is permanently fixed. The hard disk used in a higher end Pc can have a maximum storage capacity of 17 GB (Giga Byte; 1 GB= 1024 MB = 230 bytes). Now a days, hard disks capacities of 540 MB, 1 GB, 2 GB, 4 GB and 8 GB are quite common. The data transfer rate between the CPU and hard disk is much higher as compared to the between the CPU and the floppy disk drive. The CPU can use the hard disk to load programs and data as well as to store data. The hard disk is a very important Input/Output (I/O) device. The hard disk drive doesn't require any special care other than the requirement that one should operate the PC within a dust-free and cool room (preferably air- conditioned). In summary, a computer system is organized with a balanced configuration of different types of memories. The main memory (RAM) is used to store program being currently executed by the computer. Disks are used to store large data files and program files. Tapes are serial access memories and used to backup the files form the disk. CD-ROMs are used to store user manuals, large text, audio and video data.
- 18. 17 Application and System Software Software & Hardware A set of programs associated with the operation of a computer is called software. The electronic circuits used in building the computer that executes the software is known as the hardware of the computer. For example, a TV bought from a shop is hardware; the various entertainment programs transmitted from the TV station are software. An important point to note is, hardware is a one-time expense and is necessary whereas software is a continuing expense and is vital. Computer software may be classified into two broad categories: Application Software It is the set of programs necessary to carry out operations for a specified application. Example Programs • To solve a set of equations • To process examination results • To prepare a Pay-Bill for an organization • To prepare Electricity-Bill for each month. System Software These are general program written for the system, which provide the environment to facilitate writing of Application software. Some of the system programs are given below: Compiler: It is a translator system program used to translate a High-level language program into a Machine language program. Assembler: It is another translator program used to translate an Assembly language program into a Machine language program. Interpreter: It is also a translator system program used to translate a High level language program into a Machine language program, but it translates and executes line by line. Loader: It is a system program used to store the machine language program into the memory of the computer.
- 19. 18 Computer Languages Machine language The computers can execute a program written using binary digits only. This type of programs is called machine language programs. Since these programs use only '0's and '1's it will be very difficult for developing programs for complex problem solving. Also it will be very difficult for a person to understand a machine language program written by another person. At present, computer users do not write programs using machine language. Also these programs written for execution in one computer cannot be used on another type of computer. i.e., the programs were machine dependent. Assembly Language In assembly language mnemonic codes are used to develop program for problem solving. The program given below shows assembly language program to add two numbers A & B. Assembly language is designed mainly to replace each machine code with and understandable mnemonic code. To execute an assembly language program it should first be translates into an equivalent machine language program. Writing and understanding programs in assembly language is easier than that of machine language. The programs written in assembly language are also machine dependent. High Level Languages High level language are developed to allow application programs, which are machine independent. High level language permits the user to use understandable codes using the language structure. In order to execute a high-level language program, it should be translated into a machine language either using a compiler or interpreter. The high level languages commonly used are FORTRAN (FORmula TRANslation), BASIC (Beginner's All-purpose Symbolic Instruction Code), COBOL (COmmon Business Oriented Language). Recently developed programming language such as Visual Foxpro, Visual Basic (VB), Visual C++ (VC++) are more popular among the software developers. The following program written in BASIC language is to add two given numbers. Program code Description READ A ADD B STORE C PRINT C HALT It reads the value of A. The value of B is added with A. The result is store in C. The result in 'C' is printed. Stop execution.
- 20. 19 Program Code Description 10 INPUT A,B 20 LET C=A+B 30 PRINT C 40 END To read the value of A&B A&B are added and result is stored in C Print the value of C Stop execution Computers and Communications Local Area Network (LAN) & Wide Area Network (WAN) Computers available in remote locations can communicate with each other using a telecommunication line. One way of connecting the computers is by using devices called modems. A modem is used to transfer data from one computer to another using the telephone lines. A modem converts the strings of 0s and 1s into electrical signals which can be transferred over the telephone lines. Both the receiving and the transmitting computer have a telephone connection and a modem. An external modem is connected to the computer like a typical input or an output device. An internal modem is fitted into the circuitry related to the CPU and Memory. Interconnection of computers which are within the same building or nearby locations forms a network of computers and this network is called a Local Area Network (LAN). A LAN permits sharing of data files, computing resources and peripherals. Interconnection of computers located in far away locations using telecommunication system is known as Wide Area Network (WAN).
- 21. 20 COMPUTER COMMUNICATION USING TELEPHONE LINES Internet Intercommunication between computer networks is possible now. Computer networks located in different Organizations can communicate with each other through a facility know as Internet. Internet is a world wide computer network, which interconnects computer networks across countries. The Internet facilitates electronic mail (email), file-transfer between any two computers and remote access to a computer connected in the internet. This intercommunication facility has changed the style of functioning of the business organization and it has made the world a global village. So this covers the basics of computer system and its application. Now I would start with the generation of computers.
- 22. 21 First Generation Electronic Computers (1937-1953) We have already discussed about some of the early computers –ENIAC , EDVAC , EDSAC , UNIVAC I , and IBM 701.These m/cs and others of their time were built by using thousands of vaccum tubes. A vaccum tube was fragile glass device which used filaments as a source of electronics and could control and amplify electronic signals. It was the only high speed electronic switching device available in those days.These vacuum tube computers could perform computations in milliseconds, and were referred to as first generation computers. Memory was constructed using electromagnetic relays, and all data and instructions were fed into the system from punched cards.The instruction were written in m/c and assembly languages because high level programming languages were introduced much later. Characteristic Features Of First Generation 1. They were the fastest calculating device of their time 2. They were to bulky in their size, requiring large rooms for installation 3. 1000’s of vacuum tubes which were used emitted large amount of heat and burnt out frequently. Hence the rooms / areas in which these computers were located had to be properly air conditioned. 4. Each vacuum tube consumed about half watt of power. Since a computer typically used more than ten thousand vacuum tubes the power consumption of these computers was very high. 5. As vacuum tubes used filaments, they had a limited life .Since thousand of vacuum tubes were used in making one computer these computers were prone to frerquent hardware failures. 6. Due to low mean time failures, these computers required almost constant maintenance. 7. Thousands of individual components had to be assembled manually by hand into functioning ccts. Hence commercial production of these computers was difficult and costly. 8. Since these computers were difficult to program and use they had limited commercial use. Second Generation (1955-1964) The second generation saw several important developments at all levels of computer system design, from the technology used to build the basic circuits to the programming languages used to write scientific applications. Electronic switches in this era were based on discrete diode and transistor technology with a switching time of approximately 0.3 microseconds. The first machines to be built with this technology include TRADIC at Bell Laboratories in 1954 and TX-0 at MIT's Lincoln Laboratory.
- 23. 22 Transistors soon proved to be better electronic switching devices than vacuum tubes, due to their following properties. 1. They were more rugged and easy to handle than tubes, since they were made of germanium semiconductor material rather than glass. 2. They were highly reliable as compared to tubes, since they had no part like a filament, which could burn out. 3. They could switch much faster than tubes. 4. They consumed almost 1/10th the power consumed by a tube. 5. They were much smaller than a tube. 6. They were less expensive to produce. 7. They dissipated much less heat as compared to vacuum tubes. Due to the properties listed above second generation computers were more powerful, more reliable ,less expensive, smaller, and cooler to operate than the first –generation computers. Memory: is composed of the magnetic cores. Magnetic disk and magnetic tape were main secondary storage media used in secondary generation computers. Punched cards were still popular and widely used for preparing programs. During this second generation many high level programming languages were introduced, including FORTRAN (1956), ALGOL (1958), and COBOL (1959). Important commercial machines of this era include the IBM 704, the 709 and 7094. The latter introduced I/O processors for better throughput between I/O devices and main memory. Features Of Second Generation: 1. They were more than ten times faster than the first generation computers. 2. They were much smaller than first generation computers, requiring smaller spaces. 3. Although the heat dissipation was much less than first generation computers, the rooms/areas in which the second generation computers were located had to be properly air conditioned. 4. They consumed much less power than the first generation computers. 5. They were more reliable and less prone to hardware failures than the first generation computers. 6. They had faster and larger primary and secondary storage as compared to first generation computers. 7. They were much easier to program and use than the first generation computers. Hence they had wider commercial use.
- 24. 23 8. In these computers, thousands of individual transistors had to be assembled manually by hand into functioning ccts. Hence commercial production of these computers was difficult and costly. Fig Electronics devices used for manufacturing computers of different generations
- 25. 24
- 26. 25 Summary of the Generation Of the Computers THE LECTURE IN A GO !!!!!!!!!!!!! ƒ All computer systems perform the following 5 basic operations for converting raw input data into useful information- inputing, storing, processing, outputting, controlling. ƒ The input unit allows data and instruction to be fed from the outside world in computer acceptable form. ƒ The input interface transforms the data and instruction to be fed to the computer,through its input devices, into the binary codes, which are acceptable to the computer. ƒ The output unit allows the computer system to supply the information, obtained from data processing, to the outside world, in human acceptable(readable)from. ƒ The output interfaces transform the information, obtained from data processing, from binary form to human acceptable (readable) form. ƒ The storage unit of a computer system holds the data and instruction to be processed, and the intermediate and final results of processing. The 2 types of storage are Primary and Secondary storage. As compared to primary storage, secondary storage is slower in operation, larger in capacity, cheaper in price, and can retain information even when the computer system is switched off or reset. ƒ Different types of storage devices. ƒ During data processing, the actual execution of the instruction takes place in the Arithmetic Logic Unit(ALU)of a computer systems. ƒ The control unit of a computer system manages and co-ordinates the operations of all the other components the computer systems. ƒ The Control unit and the arithmetic unit Logic Unit of a computer system are jointly known as the Central Processing Unit(CPU),which serves as the brain of the computer system and is responsible for controlling the operations of all other units of the system. ƒ A computer is often referred to as computer system, because it is made up of integrated compinents(i/o ,storage, CPU),which work together to perform the steps called for, in the program being executed. ƒ Different type of storage devices ƒ Modes of communication of data. Yes with this we finish the introduction part of the computers. Now lets begin with the generations. Emerging Trends A new kid of device The biggest immediate potential for this technology would be what could be dubbed a PDN - a personal digital notebook. Unlike the much ballyhooed Tablet PC (basically a Windows laptop with touch screen and handwriting recognition), such a device would expand the Palm paradigm: simple, immediately useful and usable, with a minimal OS. Not a replacement for a laptop, but a device which allows basic management functions with note taking and document display.There are a few simple reasons for this analysis: electronic ink will, at least initially, be monochrome,
- 27. 26 and therefore appeal for usages which don’t require color in real life, such as note taking, reading, managing your date-book and so on. (It is unlikely that Windows users will settle for a monochrome version of their OS without feeling they are losing something important.) The phenomenal success of the Palm has shown that there is a market for handheld devices which don't try to rival with a complete computer. This notion could be expanded considerably, especially if the device is light and simple enough to allow for intuitive use even for a computer novice. And then there is price, of course. One of the problems with Microsoft’s conception of the Tablet PC is that it is a complete laptop - and it will come at prices of high-end portable computers, which it will only partly replace (at least initially). In order to be a genuinely useful complement to current devices, a true digital notebook would have to be both less complex and less expensive. The role of electronic paper In any case, electronic paper will play an important role in the development of next generation handheld devices: low power consumption, high contrast, a high resolution display which stays in place when a device is turned off and can be viewed in broad daylight, all these factors indicate that this technology will have a considerable impact on the devices we will find on the market. This is not going to happen overnight, however. Until the best use for this technology potential is found, electronic ink displays will find their way into a number of existing platforms, such as next generation Palms or Pocket PCs. The ultimate question is of course what the right mix of features will be: Digital Notebooks with built-in web-browsers? Course books with annotation and word-processing functions? Date books with handwriting recognition and built-in e-book readers, web browsers and GPS devices? It will take some time to sort this out - but there is a lot to be invented here…
- 28. 27 Question: 1. Hardware is one time expense but software is continuing expense. Discuss 2. You need to connect various computer systems in your college, what type of network you will establish and why. Justify your answer. 3. Can our systems work without RAM, Give reasons in support of your answer? 4. How does a normal user interact with the hardware of a computer system. Describe the various in between layers. 5. How can a business organization benefit through the use of internet. END OF TODAYS LECTURE… REFERENCES: 1. COMPUTER FUNDAMENTALS PRADEEP .K.SINHA BPB PUBLICATIONS 2. COMPUTER ORGANISATION AND ARCHITECTURE WILLIAM STALLINGS
- 29. 28 Lecture 3 Contd…… Hello! Friends , I am going to continue with the remaining generations of the computer. Now let us study about the third generation. Third Generation (1964-1975) The third generation brought huge gains in computational power. Innovations in this era include the use of integrated circuits, or ICs (semiconductor devices with several transistors built into one physical component), semiconductor memories starting to be used instead of magnetic cores, microprogramming as a technique for efficiently designing complex processors, the coming of age of pipelining and other forms of parallel processing (described in detail in Chapter CA), and the introduction of operating systems and time-sharing. The first ICs were based on small-scale integration (SSI) circuits, which had around 10 devices per circuit (or ``chip''), and evolved to the use of medium-scale integrated (MSI) circuits, which had up to 100 devices per chip. Multilayered printed circuits were developed and core memory was replaced by faster, solid state memories. Computer designers began to take advantage of parallelism by using multiple functional units, overlapping CPU and I/O operations, and pipelining (internal parallelism) in both the instruction stream and the data stream. In 1964, Seymour Cray developed the CDC 6600, which was the first architecture to use functional parallelism. By using 10 separate functional units that could operate simultaneously and 32 independent memory banks, the CDC 6600 was able to attain a computation rate of 1 million floating point operations per second (1 Mflops). Five years later CDC released the 7600, also developed by Seymour Cray. The CDC 7600, with its pipelined functional units, is considered to be the first vector processor and was capable of executing at 10 Mflops. The IBM 360/91, released during the same period, was roughly twice as fast as the CDC 660. It employed instruction look ahead, separate floating point and integer functional units and pipelined instruction stream. The IBM 360-195 was comparable to the CDC 7600, deriving much of its performance from a very fast cache memory. The SOLOMON computer, developed by Westinghouse Corporation, and the ILLIAC IV, jointly developed by Burroughs, the Department of Defense and the University of Illinois, were representative of the first parallel computers. The Texas Instrument Advanced Scientific Computer (TI-ASC) and the STAR-100 of CDC were pipelined vector processors that demonstrated the viability of that design and set the standards for subsequent vector processors.
- 30. 29 Features of Third Generation Computers are as follows: 1. They were much more powerful than the second generation computers. They were capable of performing about 1 million instruction per second. 2. They were much smaller than second generation computers, requiring smaller space 3. Although the heat dissipation was much less than second generation computers, the room in which the third generation were kept had tyo be properly air conditioned. 4. They consumed much less power. 5. They were more reliable and less prone to hardware failures than the second generation computers. Maintenance cost was much lower. 6. They had faster and larger primary and secondary storage as compared to second generation computers. 7. They were totally general purpose m/c. 8. Their manufacturining did not require manual assembly of individual components into electronic ccts, resulting in reduced human labor and cost involved at assembly stage. Commmercial production of this system were easier and cheaper. 9. Time sharing OS allowed interactive usage and simultaneous use of these systems by a larger number of users. 10. Time sharing OS made On Line systems feasible, resulting in the usage of these systems for new on-Line applications. 11. The minicomputers of the third generation made computers affordable even by smaller companies. Fourth Generation (1975-1989) The next generation of computer systems saw the use of large scale integration (LSI - 1000 devices per chip) and very large scale integration (VLSI - 100,000 devices per chip) in the construction of computing elements. At this scale entire processors will fit onto a single chip, and for simple systems the entire computer (processor, main memory, and I/O controllers) can fit on one chip. Gate delays dropped to about 1ns per gate. Semiconductor memories replaced core memories as the main memory in most systems; until this time the use of semiconductor memory in most systems was limited to registers and cache. During this period, high speed vector processors, such as the CRAY 1, CRAY X-MP and CYBER 205 dominated the high performance computing scene. Computers with large main memory, such as the CRAY 2, began to emerge. A variety of parallel architectures began to appear; however, during this period the parallel computing efforts were of a mostly experimental nature and most computational science was carried out on vector processors. Microcomputers and workstations were introduced and saw wide use as alternatives to time-shared mainframe computers. It started a new social revolution the Personal computer revolution. Overnight,
- 31. 30 computers became incredibly compact. They became inexpensive to make, suddenly it became possible for anyone to own a computer. During this generation magnetic core memories were replaced by semiconductor memories, resulting in large random access memories with very fast access time. Hard Disk became cheaper, smaller and large in capacity. In addition to magnetic tapes, floppy disks became very popular as a portable medium for porting programs and data from one computer system to another. Another feature introduced was high speed computer networking, which enabled multiple computer to be connected together .To enable to communicate with each other Local Area Networks Became Popular. During this generation UNIX operating system and C programming became popular. Features Of Fourth Generation computers 1. The PC’s were smaller and cheaper than Main Frame or Minicomputers of third generation 2. Mainframes were much more powerful. 3. No Air conditioning were required for the PC’s 4. They consumed much less power than the third generation computers 5. They were more reliable and less prone to the hardware failures , hence the maintanence cost was negligible 6. They had faster and much larger secondary and primary storage. 7. Graphical user interface (GUI) enabled new users to quickly learn how to use computers. 8. Network of computers enabled sharing of resources like disks, printers, among multiple computers and their users. 9. These systems also used add-on hardware feature. 10. They made computers affordable even by individuals for their personal use at home. Fifth Generation (1989) During this generation the VLSI technologies became ULSI (Ultra Large scale Integration) .Storage technologies also advanced very fast,making larger and larger main memory and disk storage available in newly introduced systems.During the fifth generation optical disks also emerged as a popoular portable mass storage media.They are more commonly known as CD- ROM(Compact Disk-Read Only Memory)because they are mainly used for storing programs and data,which are only read(not written/modified)
- 32. 31 Characteristic Features Of Fifth generation computers are as follows 1. Portable PCs are much more smaller and handy than PCs of the fourth generation, allowing users to use computing facility even while traveling. 2. The desktop PCs and workstations are several times more powerful than the PCs of fourth generation. 3. The mainframes are several times more powerful than the mainframes systems of the fourth generation. 4. They consume much less power than the predecessors. 5. They are more reliable and less prone to the hardware failures than their predecessors. Hence the maintenance cost is negligible 6. They have faster and larger primary and secondary storage 7. They are totally general purpose m/c 8. More user friendly 9. These systems also use the concept of unbundled software and add-on hardware, allowing the users to invest only in the hardware configuration and software of their need and value. THE LECTURES IN A GO ||||||||||||||||| 1. Important points of the Third Genrations. 2. Important points of the fourth and fifth generations. END OF TODAYS LECTURE………..
- 33. 32 REFERENCES: 1. COMPUTER FUNDAMENTALS RADEEP .K.SINHA BPB PUBLICATIONS 2. COMPUTER ORGANISATION AND ARCHITECTURE WILLIAM STALLINGS PRENTICE PUBLICATIONS
- 34. 33 Lecture 4 CLASSIFICATION OF COMPUTERS Objectives of the lecture: 1.To understand the Classification Of Computers Hello students, I am sure you all must be well versed with the generations of the computer from my previous lectures and I am sure you want to know more about it. So let us begin todays session with the defination of the computer and then I will explain the characteristics, its types and so on.. Defination: It’s a device which can operate on the data. Data could be anything like bio-data , marks obtained ,airline or railway reservations , or in use of solving scientific research problems. A computer can store , process , and retrive data as and when desired. One can even call, it as Data Processor because it processes data. Thus in short we can define it as the activity of processing data using a computer is called Data Processing. Gather data from various incoming sources, merge them in desired order, and finally print them in the desired format. Activities involved in Data Processing are :- 1. Capturing the input data. 2. Manipulating the data 3. Managing the output results. CHARACTERISTIC OF COMPUTERS 1. Automatic : Computers are automatic m/c because once started on a job they carry on until the job is finished ie it works from a program a program of coded informations which specify how exactly a particular job is done 2. Speed: It is a very fast device. It can perform in a few seconds ie a compouter does in 1 min. what would take a man his entire life. While talking about speed we mean speed in microseconds 10 to the power of –6 , the nano seconds ie 10 to the power of-9 , and even
- 35. 34 picoseconds ie 10 to the power of –12.Powerful computer performs several billion ie 10 to the power 9 simple arithmetic expressions. 3. Accurracy: Computers are very accurate. The accuracy of computer is very high , and the degree of accuracy depends upon its design. 4. Diligence : Unlike human being a computer is free from monotony , tiredness and lack of concentration. It can work for hours without creating any errors and without grumbling. 5. Versatility : It is the most important thing about a computer. One moment it is preparing a result of an examination , the next it is busy preparing bills, in between it may be helping an office secretary to trace an important letter in seconds. Briefly the computer is capable of performing any task . 6. Power of Remembering A computer can store and recall any amount of information because of its secondary storage capability. Even aftewr several years the information recalled would be as accurate as on the day when it was fed. 7. No. I.Q : The computer possess no intelligence of its own. Its I.Q is zero. at leat until today. It has to be told what to do and in what sequence. 8. No Feeling : Computers are devied of emotions. They have no feelings and no instinct because they are m/c, their judgement is based on the instructions given to them in the form of programs that are written by us. EVOLUTION OF COMPUTERS Let us discuss the history of the computers, the first mechanical adding m/c was invented by Blaise Pascal in 1642.Later in the year 1671,Baron Gottfried Wilhelm von Leibniz of germany invented the first calculator for multiplication. Herman Hollerith came up with the concept of punchedcards, which are extensively used as input medium in computers. Business m/c and calculators made their appearance in Europe and America towards end of 19 th centuray. Charles Babbage a 19 th century Professor at Cambridge University , is considered the father of modern digital computers. Babbage had to spend several hours checking these tables which made his job difficult , as a result he started to build a m/c , which could compute tables guaranteed to
- 36. 35 be error free. In 1822 he designed a “Difference Engine” which produce reliable tables. And in 1842 Babbage came out with his idea of analytical engine. Let us now briefly discuss about some of well known early computers:- 1. The Mark I Computer : Known as Automatic Sequence Controlled Calculator, this was the first fully Automatic calculating m/c designed by Howard a. Aiken of Harvard University, in collaboration with IBM .It was based on the concept of punched cards. Although it was very complex in design and huge in size .It used 3000 electrically actuated switches to control its operations and was approx, 50 feet long and 8 feet high. 2. Atans off – Berry Computer: This was developed by Dr.John Atansoff to solve mathematical equation. I t was called ABC computers.It used 45 vacuum tubes for internal logic and capacitors for storage 3. The ENIAC (1943-46): This is the first Electronic Numerical Integrator and Computer designed and constructed under the supervision of John Mauchly and John Presper Eckert at the university of Pennsylvania,was the worlds first general purposeelectronic digital computer.This project was a response to U.S. wartime needs The Army’s Ballistics Research Laboratory(BRL),an agency responsible for developing range trajectory tables for new wepons, was having difficulty supplying these tables accurately and within a reasonable time frame. The BRL employed more than 200 people , mostly women who using desktop calculators, solved the necessary balastic equations. Preparation of the tables for a single weapon would take one person many hours, even days. 4. Mauchly, a professor of electrical engineering at the university and Eckert one of this graduate students, proposed to build general purpose computer using vacuum tubes to be used for the BRL’s application. The resulting m/c was enormous weighing 30 tones, occupying 15,000 square feet, having more than 18,000 vacuum tubes it consumed 140 kilowatts of power. It was also faster than any electromechanical computer, being capable of 5000 additions per second. 5. The EDVAC (1946-52): (Electronic Discrete Variable Automatic Computer)A major drawback of ENIAC was that its programs were wired on boards which made it difficult to change the programs. This problem was later over commed by Dr. John Neumann. Basic idea behind this concept was that the sequence of instruction and the data can be stored in the memory of the computer.
- 37. 36 VON NEUMANN MACHINE As mentioned above the task of entering and altering programs for ENIAC was extremely tedious.The programming process could be facilitated if the programs could be represented in the form suitable for storing in memory alongside the data.Then a computer could get its instruction by reading them from memory and a program could be set or altered by setting the values of a portion of memory.This idea known as stored program concept is usually attributed to ENIAC designers,most notably the mathematician John Von Neumann,who was the consultant on the ENIAC project.The first publication of the idea was in 1945 proposal by von Neumann for a new computer,the EDVAC(Electronic Discrete Variable Computer) Von Neumann and his colleagues began the design of new stored program computer,referred to as the IAS computer, General Structure of the IAS computer. • A main memory which stores data and instructions • An arithmetic and logical unit(ALU) capable of operating on binary data. • A control unit , which interprets the instruction in memory an dcauses them to be executed. • Input and Output(I/O) equipment operated by control unit.
- 38. 37 Fig 1 Structure Of the IAS Computer Explanation of the above: • Since the device is primarily a computer it will have to perform the elementary operations of arithmetic most frequently. These addition, subtraction, multiplication and divisions: +,-,x,.are taken care by central arithmetical part of the device. ie CA • The Logical control of the device that is the proper sequencing of its operations, is most efficiently carried by a central control organ ie CC • Any device which is to carry out long and complicated sequences of operations must have a considerable memory. ie M • The above three specific parts CA, CCie(C),M constitute the input and output devices. • The devices must be endowed with the ability to maintain input and output contact with some specific medium of this type. The medium will be called the outside recording medium of the device :R • The device must have some organ to transfer information from R into its specific parts C and M. ie I • The device must have some organ to transfer from C ,M into R. ie O. | | | M | |____________| ^ _______________________| _________ | ___________ _____v______ | ____________ _____ | | | | | | | | | | | CA |<->| CC <->| I/O <->| nerd | | |___________| |____________| | |____________| |_____ Main Memory Arithmetic LogicUnit Program Control Unit I/O Equi- ment
- 39. 38 All of todays computers have this same general structure and function and are therefore referred to as Von Neumann m/c. Following is the IAS memory formats 0 1 39 a) Number Word sign bit b) Instruction Word 0 8 19 28 39 Op code Address Op code Address Fig Expanded structure of the IAS computer
- 40. 39 According to the above fig. • (MBR) Memory Buffer Register : Contains the word to be stored in memory , or is used to receive a word from memory. • (MAR) Memory Address Register: Specifies the address in the memory of the word to be written from or read into the MBR. • (IR)Instruction register: Contains the 8 bit opcode instruction being executed • (IBR)Instruction Buffer Register: Employed to temporartily hold the right –hand instruction from a word in memory. • (PC)Program counter: Contains the address of the next instruction-pair to be fetched from memory. • (AC)Accumulator and Multiplier-Quotient(MQ):Employed to temporarily hold operands and results of ALU operations. For eg. The result of multiplying two 40-bit numbers is an 80-bit number;the most significant 40 bits are stored in AC and the least significant in the MQ. 6. The EDSAC(1947 – 49) (Electronic delay storage automatic Calculator. This m/c was developed by a group of scientest headed by the professor Maurice Wilkes. In this m/c addition operation was accomplished in 1500 microseconds and multiplication operation in 4000 microseconds. 7. UNIVAC(1951) : It’s a Universal Automatic Computer was the first digital computer, which was not “one of the kind” . The first Was installed and used continuously for 10 yrs. In 1952 the international Business m/c corp.introduced the 701 commercial computer.. Emerging Trends The study of artificial self replicating systems was first pursued by von Neumann in the 1940's. Subsequent work, including a study by NASA in 1980, confirmed and extended the basic insights of von Neumann. More recent work by Drexler continued this trend and applied the concepts to molecular scale systems Drexler's architecture for an assembler Drexler's assembler follows the Von Neumann architecture, but is specialized for dealing with systems made of atoms. The essential components in Drexler's Assembler are shown in figure 2. The emphasis here (in contrast to von Neumann's proposal) is on small size. The computer and constructor both shrink to the molecular scale, while the constructor takes on additional detail consistent with the desire to manipulate molecular structures with atomic precision. The molecular constructor has two major subsystems: (1) a positional capability and (2) the "tip chemistry."
- 41. 40 Figure 2. The positional capability might be provided by one or more small robotic arms, or alternatively might be provided by any one of a wide range of devices that provide positional control[14]. The emphasis, though, is on a positional device that is very small in scale: perhaps 0.1 microns (100 nanometers) or so in size. As an aside, current SPM (Scanning Probe Microscope) designs employ piezoelectric elements for positional control[21]. A rather obvious question to ask is: why prefer mechanical positioning systems over piezoelectric or other electrostatic devices? The reasons for using basically mechanical devices at the molecular scale are similar to the reasons that mechanical devices are employed at the macroscopic scale: the desire for compactness and high positional accuracy (e.g., high stiffness). This weighs against electrostatic and piezoelectric devices. Molecular mechanical devices, on the other hand, can employ very stiff materials and, with appropriate design, can have joints that can rotate easily but which at the same time provide high stiffness in other degrees of freedom [1,20] The "tip chemistry" is logically similar to the ability of the Von Neumann Universal Constructor to alter the state of a cell at the tip of the arm, but here the change in "state" must correspond to a real world change in molecular structure. That is, we must specify a set of well defined chemical reactions that take place at the tip of the arm, and this well defined set of chemical reactions must be sufficient to allow the synthesis of the class of structures of interest. The assembler, as defined here, is not a specific device but is instead a class of devices. Specific members of this class will deal with specific issues in specific ways.
- 42. 41 THE LECTURE IN A GO|||||||||| 1. A computer is normally considered to be a calculating device, which can perform arithmetic at enormous speed.It is also known as a data processor since it not only computes in a usual sense, but also performs other functions with the data. 2. The activity of processing data using a computer is called data processing. Data is the raw material used as input to data processing, and information is processed data obtained as the output of data processing. 3. Computers are characterized by their being automatic, speed and accuracy of computing, diligence, versatility, power of remembering and lack of intelligence and feelings. 4. Charles Babbage is considered the father of modern digital computers. 5. Some of the well known early computers are the Mark1, Atanasoft-Berry, the ENIAC, the EDVAC, the EDSAC, the UNIVAC 1. 6. Dr. John Von Neumann introduced the “stored program” concept which considerably influenced the development of modern digital computers .Due to this features we often refer to modern digital computers as stored program digital computers.
- 43. 42 END OF TODAYS LECTURE…… REFERENCES: 1. COMPUTER FUNDAMENTALS PRADEEP .K.SINHA BPB PUBLICATIONS 2. COMPUTER ORGANISATION AND ARCHITECTURE WILLIAM STALLINGS PRENTICE HALL OF INDIA
- 44. 43 Lecture 5 ORGANISATION / STRUCTURE /FUNCTION Objectives of the lecture: 1.To understand the Organisation / Structure /Function Hello! students, today we will learn about the structure and function of computers. which will help you to know about about CPU, Registers, Control Unit, ALU, along with this about the performance factors . The intent of this lecture is to provide a discussion of the fundamentals of computer organization, structure and function . Organization and architecture In describing computer systems, a distinction is often made between computer architecture and computer organization. Although it is difficult to give precise definitions for these terms, a consensus exists about the general areas covered by each (e.g., [VRAN80], [SIEW82], and [BELL78a]. Computer architecture ™ It refers to those attributes of a system visible to a programmer, or ™ Those attributes that have a direct impact on the logical execution of a program. • Computer organization ™ It refers to the operational units and their interconnections that realize the architectural specifications. • Examples of architectural attributes include ---The instruction set, the number of bits used to represent various data types (e.g., numbers, characters), I/O mechanisms, and techniques for addressing memory. Example Of Organizational attributes include ---Those hardware details transparent to the programmer, such as control signals, interfaces between the computer and peripherals, and the memory technology used. As an example, it is an architectural design issue whether a computer will have a multiply instruction. It is an organizational issue whether that instruction will be implemented by a special multiply unit or by a mechanism that makes repeated use of the add unit of the system. The organizational decision may be based on the anticipated frequency of use of the multiply
- 45. 44 instruction, the relative speed of the two approaches, and the cost and physical size of a special multiply unit. Historically, and still today, the distinction between architecture and organization has been an important one. Many computer manufacturers offer a family of computer models, all with the same architecture but with differences in organization. Consequently, the different models in the family have different price and performance characteristics. Furthermore, an architecture may survive many years, but its organization changes with changing technology. A prominent example of both these phenomena is the IBM System/370 architecture. This architecture was first introduced in 1970 and included a number of models. The customer with modest requirements could buy a cheaper, slower model and, if demand increased, later upgrade to a more expensive, faster model without having to abandon software that had already been developed. Over the years, IBM has introduced many new models with improved technology to replace older models, offering the customer greater speed, lower cost, or both. These newer models retained the same architecture so that the customer’s software investment was protected. Remarkably, the System / 370 architecture, with a few enhancements, has survived to this day and continues as the flagship of IBM’s product life. In a class of systems called microcomputers, the relationship between architecture and organization is very close. Changes in technology not only influence organizational but also result in the introduction of more powerful and richer architectures. Generally, there is less of a requirement for generation-to-generation compatibility for these smaller machines. Thus, there is more of an interplay between organizational and architectural design decisions. An intriguing example of this is the reduced instruction set computer (RISC). STRUCTURE AND FUNCTION A computer is a complex system; contemporary computers contain millions of elementary electronic components. How, then, can one clearly describe them? The key is to recognize the hierarchic nature of most complex systems, including the computer [SIMO069]. A hierarchic system is a set of interrelated subsystem, each of the latter, in turn, hierarchic in structure until we reach some lowest level of elementary subsystem. The hierarchic nature of complex system is essential to both their design and their description. The designer need only deal with a particular level of the system at a time. At each level, the system consists of a set of components and their interrelationships. The behavior at each level depends only on a simplified, abstracted characterization of the system a the next lower level. At each level, the designer is concerned with structure and function Structure : The way in which the components are related. Function: The operation of each individual component as part of the structure. FUNCTION: There are four functions : 1. Data Processing 2. Data Storage
- 46. 45 3. Data Movement 4. Control The computer must be able to --- Store data : There is short term data storage , long term data storage function. File of data are Stored on the computer for subsequent retrieval and update. Process data : The computer must be able to process data Move data : The computer must be able to move data between itself and outside world. The computer Operating environment consists of devices that serve as either sources or destination of data. When the data are received from or delivered to a device that is directly connected to the computer the process is known as INPUT /OUTPUT (i/o) and the device is refered to as peripherals. When data are moved over long distance to or from a remote devices, the process is known as DATA COMMUNICATION . Finally there must be some control between them which is provided by the individuals who provide the computer with the instructions.CONTROL UNIT manages the computers resources and orchestrates the performance of its functional parts in response to those instructions. The number of possible operations that can be performed as follows: • The computer can function as the data movement device • It can simply transfer data from one peripheral or communications line to another. • It can also function as data storage device, with data transferred from external environment to computer storage(read) and vice versa(write). • Finally involving data processing, on data either in storage or en route between storage and external environment.
- 47. 46 Fig. A Functional View Of The Computer. Fig Possible computer operations
- 48. 47 STRUCTURE The computer is an entity that interacts with its external environment.In general all its linkages to the external environment can be classified as peripheral devices or communication lines.There are four main structural components. • Central Processing Unit(CPU) : Controls the operation of the computer and performs its data processing functions.Simply referred to as Processors. • Main memory : Store data. • I/O : Moves data between computer and its external environment • System Interconnection : Some mechanism that provides for communication among CPU, main memory,and I/O. There may be one or more of each of the above components.Traditionally , there has been just a single CPU. Its major structural components are : ™ Control Unit : Controls the operation of the CPU and hence the computer ™ Arithmetic and Logic Unit (ALU) : Performs the computers data processing functions. ™ Registers: Provides storage internal to the CPU ™ CPU Inter connection : Some mechanism that provides for communication among the control unit ,ALU and registers. COMPUTER STORAGE PROCESSING Communication lines Fig : The Computer Peripherals Fig:
- 49. 48 Fig: The computer top –level structure Computer Components Virtually all contemporary computer designs are based on concepts developed by John Von Neumann at the Institute for Advanced Studies, Princeton. Such a design is referred to as the von Neumann architecture and is based on three key concepts: Data and instructions are stored in a single read-write memory. The contents of this memory are addressable by location, without regard to the type of data contained there. • Execution occurs in a sequential fashion from one instruction to the next. There is a small set of basic logic components that can be combined in various ways to store binary data and to perform arithmetic and logical operations on that data. The system accepts data and control signal and produces results. The control signals are supplied by a program (a sequence of steps). At each step, some arithmetic or logical operation is performed on some data. As a result there are two major components of a system: an instruction interpreter and a module of general-purpose arithmetic and logic functions. Theses two components constitute the CPU. In addition, data and instructions must be put into the system and a means of reporting results is needed. Therefore we need an input module and an output module. These are referred to as I/O components. The computer also needs a main memory module which is a place to temporarily store both instructions and data. It includes • A main memory which stores both data and instructions • An arithmetic-logical unit (ALU) capable of operating on binary data • A control unit which interprets the instructions in memory and causes them to be executed • Input and output (I/O) equipment operated by the control unit. With rare exceptions, most of today’s computers have this same general structure and function and are thus referred to as von Neumann machines. The memory of a computer consists of storage locations, called words, of binary bits. Both data and instructions are stored there. The control unit operates the computer by fetching instructions
- 50. 49 from memory and executing them one at a time. Both the control unit and the ALU contain storage locations, called registers. CPU FACTORS AFFECTING THE PERFORMANCE FACTORS: • Performance is specific to a particular program • Total execution time is a consistent summary of performance • Performance doesn’t depend on any single factor: need to know Instruction Count, Clocks Per Instruction and Clock Rate to get valid estimations • For a given architecture performance increases come from: increases in clock rate (without adverse CPI affects) – improvements in processor organization that lower CPI compiler enhancements that lower CPI and/or instruction count • Pitfall: expecting improvement in one aspect of a machine’s performance to affect the total performance Performance Calculation (1/2) • CPU execution time for program = Clock Cycles for program x Clock Cycle Time • Substituting for clock cycles: CPU execution time for program = (Instruction Count x CPI) x Clock Cycle Time = Instruction Count x CPI x Clock Cycle Time CPU ALU Internal CPU Bus Control Unit Regist ers ALU Internal CPU Bus Control Unit Regist ers
- 51. 50 How to estimate a performance of computer? One of the generic measures is MIPS (millions of instructions per second). This is only meaningful when comparing machines with the same architecture, since some architectures may require substantially more instructions than others for the same program. This method also can be very dependent on the mix of instructions and hence on the program used to measure MIPS. Some manufacturers report "peak MIPS" on carefully designed but useless programs. It is obvious, that all major computer components such as CPU, memory and IO devices together affect computer's performance. Slow RAM or hard disk is going to be a bottleneck for fast CPU. In reality, however, high performance of PC is always a trade off to low cost: Option High performance Low cost Bus architecture Separate address/data Multiplex address/data Data bus width Wider means faster Low pin count is cheaper Bus masters Multiple (requires arbitration) Single (no arbitration) Transfer size Multiple words Single word Clocking Synchronous Asynchronous Let's take a look at the factors that influence computer performance in more detail: 1. The CPU. CPU architecture is important. The higher the generation, the better. For example, because of high performance new features, Pentium 75 (fifth generation with the clock rate 75 MHz) outperforms 80486DX100 (which is the fourth generation CPU with the clock rate 100MHz). One of the techniques, enhancing the performance , is parallel processing. For example, while an instruction is being executed in the ALU (E), the next instruction can be fetched from memory (F) and decoded (D). Instruction Prefetching is another idea, first appeared in 286 (6 byte prefetching). It is based on the fact, that CPU is normally performing sequential code fetching. Only jump instructions alter program flow and they are statistically rare.Rather than wait for the execution unit to request next instruction fetch, CPU during next cycle prefetches the next instruction from memory and put it into prefetch queue to have it ready. If jump instruction is executed the information in prefetch queue is marked as invalid.
- 52. 51 2. Data bus width. 80486 processors have data bus 32 bits wide, whereas Pentiums are 64 bit processors, thus Pentiums can transfer twice as much data at a time compared to fourth generation CPUs. 3. Clock rate. Since any step of processing can happen only on the "tick" of the clock , the faster the rate the quicker the CPU works. 4. Memory. The diagram illustrates a general memory ierarchy of PC: The amount of RAM really depends on your applications. Reasonable performance today calls for 128 MB. Adding more RAM will speed up the performance if you run several applications at the same time or work with large files and documents. L1 cache resides on-chip. The bigger the on-chip cache size - the better, since more instructions and data can be stored on the chip, reducing the number of times the processor has to access slower off-chip memory areas to get data. 5. IO devices Speaking of effective interfacing I/O devices to CPU, synchronous protocol (includes a clock in the control lines) is more effective than asynchronous. A synchronous interface means data and address are transmitted relative to the clock. Since little or no logic is needed to decide what to do next, a synchronous interface can be both fast and inexpencive. A disadvantage of this protocol is that it can not be long because of the clock-skew problem. An asynchronous interface does not need clock. Instead, self-timed, handshaking protocols are used between sender and receiver.
- 53. 52 Most I/O devices today are interrupt-driven , i.e. CPU does not do anything for the I/O device until it notifies the CPU by sending interrupt (IRQ). First computers used polling - a simple interface, when the CPU periodically checked status bits to see if it is time for the next I/O operation. Since CPU is much faster than any I/O device, it is obvious that polling is a waste of the CPU's time. In general-purpose applications, using IRQ is the key to multitasking operating systems and good response time. Since I/O events often involve block transfers, direct memory access (DMA) hardware is added to many computer systems. DMA is when I/O device acts as a master and transfers large number of words to/from memory without intervention by the CPU. THE LECTURES IN A GO|||||||||| ƒ Defination Of Computer Architecture. ƒ Defination Of Computer Organisation ƒ Examples Of Architectural Attribute ƒ Examples Of Organisational Attribute ƒ Functions Of Computer and its Functional View ƒ Structure and Its Four Components QUESTIONS: 1.The performance of two different computers A and B (having similar architecture) are being compared by a consultant as part of the evaluation process, computer A operates at 100MHz clock and gives 100 MIPS whereas Computer B operates at 120MHz clock and give 80 MIPS. Due to various reasons Computer B was chosen by the consultant. He also came out with few suggestions for improving the performance of Computer B in future design modifications. Some of his suggestions are given below.
- 54. 53 (a) Replace the existing main memory with the faster memory (b) Introduce a small cache memory (c) Increase the clock frequency to 200 MHz. Suppose u are asked to select one of these suggestions, keeping the cost as the main factor. Which one will u select (a, b, c). END OF TODAYS LECTURE… REFERENCES: 1. COMPUTER FUNDAMENTALS PRADEEP .K.SINHAB PUBLICATIONS 2. COMPUTER ORGANISATION AND ARCHITECTURE WILLIAM STALLINGS RENTICE HALL OF INDIA
- 55. 54 Lecture 6 SYSTEM BUS / BUS STRUCTURE Objectives of the Lecture 1. To understand SYSTEM BUS and its role. 2. To understand BUS STRUCTURE and its importance. I hope by now you are very well able to under stand what a computer is and the long journey that we had been to achieve the current status of the computers. n this unit of computer systems, I will tell you the basic architecture of a computer. hen I say basic architecture it means how all a computer works .It is just like architecture of a house or an organization, so as to utilize space and available optimally. ere also the theme would be more or less same however the parameters may differ. can understand the kind of curiosity that you must be having on this particular aspect of computers and it is even more when you already know the components, a computer consist of but now you must be started thinking of how these components are working .I know your mind must have been crimped of by following questions: 1. What happens actually when we just click on an icon and it starts working? 2. When I give an instruction to perform a mathematical problem, how all the computer actually performs it? 3. When I save a data in the disc, how all it is saved ? 4. How the OS performs its jobs? And may be a lot more questions could have been aroused in your mind. I hope after this unit you would be able to understand these basic concepts. Let me brief you a few important concepts: At a top level, a computer consists of CPU, memory and I/O components, with one or more modules of each type. These components are interconnected in some fashion to achieve the basic function of the computer, which is to execute programs. Thus at a top level, we can describe a computer system by (1) Describing it exchanges with other components, and (2) Describing the inter connection structure and the controls required to manage the use of interconnection structure.
- 56. 55 This top-level view of structure and function is important because of its explanatory power in understanding the nature of a computer. Equally important is its use to understand the increasingly complex issues of performance evaluation. A grasp of the top-level structure and function offers insight into system bottlenecks, alternate pathways, the magnitude of system failures if a component fails, and the ease of adding performance enhancements. In many cases, requirements for greater system power and fail-safe capabilities are being met by changing the design rather than merely increasing the speed and reliability of individual components. WE are then prepared to examine the use of buses to interconnect system components. COMPUTER COMPONENTS Virtually all-contemporary computer designs are based on concepts developed by john von Neumann at the institute for advanced studies, Princeton which I have already discussed with you in the previous chapter. Such a design is referred to as the von New mann architecture and is based on three key concepts that I hope you can recollect: ™ Data and instructions are stored in single read-write memory. ™ The contents of this memory are addressable by location, without a regard to the type of data contained there. ™ Execution occurs in a sequential fashion (unless explicitly modified) from one instruction to the next. The reasoning behind these concepts was discussed already but is worth summarizing here. There is a small set of basic logic components that can be combined in various ways to store binary data and to perform arithmetic and logical operations on that data. If there is a particular computation to be performed, a configuration of logic components design specifically for that computation can be constructed. We can think of the process of connecting together the various components in the desired configuration as a form of programming. The resulting “program” is in the form of hardware and is termed a hard-wired program. If all programming were done in this fashion, very little use would be made of this type of hardware. But now let us consider this alternative. Suppose we construct a general-purpose configuration of arithmetic and logic functions. This set of hardware will perform various functions on data depending on control signals applied to the hardware. In the original case of customized hardware, the system accepts data and produces results. With general-purpose hardware, the system accepts data and control signals and produces results. Thus, instead of rewiring the hardware for each new program, the programmer merely needs to supply a new set of control signals.
- 57. 56 Customized Hardware Sequence of Data Arithmetic Results And Logic Functions (a) Programming in Hardware Instruction Codes Instruction Interpreter Control Signals General- Purpose Arithmetic and Data Logic Functions Results (b)Programming in software FIGURE : Hardware and software approaches
- 58. 57 FIGURE :Computer Components-Top Level View COMPUTER FUNCTION Now let me tell you some of the facts regarding the basic function performed by a computer in program execution. The program to be executed consists of a set of instruction stored in memory. The central progressing unit (CPU) does the actual work by executing instruction specified in the program.
- 59. 58 In order to gain a greater understanding of this function and of the way in which the major components of the computer interact to execute a program, we need to look in more detail at the process of program execution. The simplest point of view is to consider instruction processing as consisting of two steps: The CPU reads (fetches) instructions from memory one at a time, and it executes each instruction. Program execution consists of repeating the process of instruction fetch and instruction execution. Of course the execution of an instruction may itself involve a number of steps. At this stage, we can justify the breakdown of instruction processing into the two stages of fetch and execution as follows: 1. The instruction fetch is a common operation for each instruction, and consists of reading an instruction from location in memory. 2. The instruction execution may involve several operations and depends on the nature of the instruction. The processing required for a single instruction is called an Instruction Cycle. Using the simplified two-steps description explained above, the instruction cycles is depicted .The two steps are referred to as the Fetch Cycle and the Execute Cycle. Program execution halts only if the machine is turned off, some sort of unrecoverable error occurs, or a program instruction that halts the computer is encountered. FIGURE :BASIC INSTRUCTION CYCLE
- 60. 59 System bus, Bus Structure Now I think you are in a position to understand the concept of buses which is one of the major building blocks of CA. BUSES • There are a number of possible interconnection systems • Single and multiple BUS structures are most common • e.g. Control/Address/Data bus (PC) • e.g. Unibus (DEC-PDP What is a Bus? • A communication pathway connecting two or more devices • Usually broadcast • Often grouped A number of channels in one bus e.g. 32 bit data bus is 32 separate single bit channels • Power lines may not be shown A bus is a communication pathway connecting two or more devices. A key characteristic of a bus is that it is a shared transmission medium. Multiple devices connect to the bus, and a signal transmitted by any one device is available for the same time period, their signals will overlap and become garbled. Thus, only one device at a time can successfully transmit. In many cases, a bus actually consists of multiple communication pathways, or lines. Each line is capable of transmitting signals representing binary 1 and binary0. Over time, a sequence of binary digits can be transmitted across a single line. Taken together, several lines of a bus can be used to transmit binary digits simultaneously (in parallel). For example, an 8-bit unit of data can be transmitted over eight bus lines. Computer systems contain a number of different buses that provide pathways between components at various levels of the computer system hierarchy. A bus that connects major computer components (CPU, memory, I/O) is called a system bus. The more common computer interconnection structures are based on the use of one more system buses. Bus Structure A system bus consists, typically, of form 50 to 100 separate lines. Each line is assigned a particular meaning or function. Although there are many different bus designs, on any bus the lines can be classified into three functional groups: data, address, and control lines. In addition, there may be power distribution lines that supply power to the attached modules. The data lines provide a path for moving data between system modules. These lines, collectively are called the data bus. The data bus typically consists of 8,16, or 32 separate lines, the number of lines being referred to as the width of the data bus.
- 61. 60 Since each line can carry only 1 bit at a time, the number of lines determines how many bits can be transferred at a time. The width of the data bus is a key factor in determining overall system performance. For example, if the data bus is 8 bits wide, and each instruction is 16 bits long, then the CPU must access the memory module twice during each instruction cycle. The address lines are used to designate the source of destination of the data on the data bus. For example, if the CPU wishes to read a word (8,16, or 32 bits) of data from memory, it puts the address of the desired word on the address lines. Clearly, the width of the address bus determines the maximum possible memory capacity of the system. Furthermore, the address lines are generally also used to address I/O ports. Typically, the higher – order bits are used to select a particular module on the bus, and the lower – order bits select a memory location or I/O port within the module. For example, on an 8-bit bus, address 01111111 and below might reference locations in a memory module (module 0) with 128 words of memory, and address 10000000 and above refer to devices attached to an I/O module (module 1.) The control lines are used to control the access to and the use of the data and address lines. Since the data and address lines are shared by all components, there must be a means of controlling their use. Control signals transmit both command and timing information between system modules. Timing signals indicate the validity of data and address information. Command signals specify operations to be performed. Typical control lines include. • Memory Write: Causes data on the bus to be written into the addressed location. • Memory Read: Causes data from the addressed location to be placed on the bus. • I/O Write: Causes data on the bus to be output to the addressed I/O port • I/O Read: Causes data from the addressed I/O port to placed on the bus. • Transfer ACK: Indicates that data have been accepted from or placed on the bus. • Bus Request: Indicates that a module needs to gain control of the bus. • Bus Grant: Indicates that a requesting module has been granted control of the bus. • Interrupt Request: Indicates that an interrupt is pending. • Interrupt ACK: Acknowledge that the pending interrupt has been recognized. • Clock: Used to synchronize operations. • Reset: Initializes all modules The operation of the bus is as follows. If one modules wishes to send data to another, it must do two things: (1) obtain the use of the bus, and (2) transfer data via the bus. If one module wishes to request data from another module, it must (1) obtain the use of the bus, and (2) transfer a request to the other module over the appropriate control and address lines. It must then wait for that second module to send the data.
- 62. 61 FIGURE: Instruction cycle state diagram THE Lecture IN A GO ! ! ! ! ! ! ! ! ! ! ! ! ! 1. Program Concept • Hardwired systems are inflexible • General purpose hardware can do different tasks, given correct control signals • Instead of re-wiring, supply a new set of control signals What is a program? • A sequence of steps • For each step, an arithmetic or logical operation is done • For each operation, a different set of control signals is needed 2. Function of Control Unit • For each operation a unique code is provided e.g. ADD, MOVE • A hardware segment accepts the code and issues the control signals
- 63. 62 • We have a computer! 3. ComponentsThe Control Unit and the Arithmetic and Logic Unit constitute the Central Processing Unit • Data and instructions need to get into the system and results out Input/output • Temporary storage of code and results is needed Main memory FIGURE: Computer Components-Top Level View 4. Instruction Cycle • Two steps: Fetch Execute
- 64. 63 5. Fetch Cycle • Program Counter (PC) holds address of next instruction to fetch • Processor fetches instruction from memory location pointed to by PC • Increment PC Unless told otherwise • Instruction loaded into Instruction Register (IR) • Processor interprets instruction and performs required actions 6. Execute Cycle • Processor-memory data transfer between CPU and main memory • Processor I/O Data transfer between CPU and I/O module • Data processing Some arithmetic or logical operation on data • Control Alteration of sequence of operations e.g. jump • Combination of above
- 65. 64 7. Example of Program Execution
- 66. 65 8. Instruction Cycle - State Diagram 9. Buses • There are a number of possible interconnection systems • Single and multiple BUS structures are most common • e.g. Control/Address/Data bus (PC) • e.g. Unibus (DEC-PDP) 10. What is a Bus? • A communication pathway connecting two or more devices • Usually broadcast • Often grouped A number of channels in one bus e.g. 32 bit data bus is 32 separate single bit channels • Power lines may not be shown 11. Data BusCarries data
- 67. 66 Remember that there is no difference between “data” and “instruction” at this level • Width is a key determinant of performance 8, 16, 32, 64 bit 12. Address bus • Identify the source or destination of data • e.g. CPU needs to read an instruction (data) from a given location in memory • Bus width determines maximum memory capacity of system e.g. 8080 has 16 bit address bus giving 64k address space 13. Control Bus • Control and timing information Memory read/write signal Interrupt request Clock signals 14. Bus Interconnection Scheme 15. Big and Yellow?What do buses look like? Parallel lines on circuit boards Ribbon cables Strip connectors on mother boards e.g. PCI Sets of wires
- 68. 67 16. Single Bus Problems • Lots of devices on one bus leads to: Propagation delays Long data paths mean that co-ordination of bus use can adversely affect performance If aggregate data transfer approaches bus capacity • Most systems use multiple buses to overcome these problems 17. High Performance Bus
- 69. 68 EXERCISE FOR U 1. One processor never uses 100% of the available bus-time. Therefore what happens if more processors want to use the same bus? 2. The processor with the lowest priority will never get the bus. It will probably generate which type of error. 3. If more performance is needed, faster processors can be used or you can enhance bus bandwidth by going from 8 to 16, 32 and even 64 bit data transfers. The use of cache may enhance overall system performance. However, there is an end to what technology can do for you today and if one processor is not enough, why not use several? 4. Two very fundamental different solutions are in use to solve the problem of bus contention in multiprocessor systems. The first solution uses cache to reduce the bus load (Profile 2). The other puts enough memory on a particular board. All program code is then located there and no more code execution bus-traffic is needed. 5. Each processor has a number of address, data and control lines to connect to memory and peripheral devices. If you design a board with all these components, what is your measurement point? References: Books Books 1. Computer Organization and Architecture By: William stallings (Preferred) 2. Computer System Architecture By: M.Morris Mano 3. Computer Architecture: A Quantitative Approach By: John L. Hennessy, David A. Patterson, David Goldberg 4. Computer Organization and Design Second Edition : The Hardware/Software Interface By : David Patterson, John Hennessy 5. Computer Architecture and Organisation By : J.P.Hayes
- 70. 69 Lecture 7 ELEMENTS OF BUS DESIGN Objectives of the Lecture 1. To understand concepts of BUS DESIGN. 2. 2. To understand ELEMENTS OF BUS DESIGN and its importance. Today I will discuss some very important aspects about system bus.In my previous lecture ,I hope you are able to understand what a bus is and its role.Now I will tell you the elements or aspects taken into consideration while designing a bus.I am providing below a table which consist of most important elements of bus design: ELEMENTS OF BUS DESGIN Type Bus Width Dedicated Address Multiplexed Data Method of Arbitration Data Transfer Type Centralized Read Distributed Write Timing Read-modify-write Synchronous Read-after-write Asynchronous Block Now let us discuss each one of them in detail: Bus Types Bus lines can be separated into two generic types: dedicated and multiplexed. A dedicated bus lines is permanently assigned either to one function or to a physical subset of computer components • Dedicated Separate data & address lines
- 71. 70 • Multiplexed Shared lines Address valid or data valid control line Advantage - fewer lines Disadvantages More complex control Ultimate performance Method of Arbitration In all but the simplest systems, more than one module may need control of the bus. For example, an I/O module may need to read or write directly to memory, without sending the data to the CPU. Since only one unit at a time can successfully transmit over the bus, some method of arbitration is needed. The various methods can be roughly classified as being either centralized or distributed. In a centralized scheme, a single hardware device, referred to as bus controller or arbiter, is responsible for allocating time on the bus. The device may be a separate module or part of the CPU. In a distributed scheme, there is no central controller. Rather, each module contains access control logic and the modules act together to share the bus. With both methods of arbitration, the purpose is to designate one device, either the CPU or an I/O module, as master. The master may then initiate a data transfer (e.g. read or write) with some other device, which acts as slave for this particular exchange. Timing Timing refers to the way in which events are coordinated on the bus. With synchronous timing, the occurrence of events on the bus is determined by a clock. The bud includes a clock line upon which a clock transmits a regular sequence of alternating 1s and 0s of equal duration. A single 1- 0 transmission is referred to as a clock cycle or bus cycle and defines a time slot. All other devices on the bus can read the clock line, and all events start at the beginning of a clock cycle.
- 72. 71 Clock • Start • Read • Address • Lines Data • Lines Acknowledge • (a) Synchronous Timing MSYN • SSYN • Read • Address • Lines Data • Lines (b) Asynchronous Timing FIGURE : Timing a read operation Bus Width We have already addressed the concept of bus width. The width of the data bus has an impact on system performance: the wider the data bus, the greater the number of bits transferred at one time. The width of the address bus has an impact on system capacity: the wider the address bus, the greater the range of locations that can be referenced. Data Transfer Type Finally, a bus support various data transfer types, as illustrated in Figure 3.20. All buses support both write (master to slave) and read (slave to master) transfers. In the case of a multiplexed address/data bus, the bus is first used for specifying the address and then for transferring the data. For a read operation, there is typically a wait while the data is being fetched from the slave to be put on the bus. For either a read or a write, there may also be a delay if it is necessary to go
- 73. 72 through arbitration to gain control of the bus for the remainder of the operation (i.e., seize the bus to request a read or write, then seize the bus again to perform a read or write. THE Lecture IN A GO ! ! ! ! ! ! ! ! ! ! ! ! ! 1. Bus TypesDedicated Separate data & address lines ƒ Multiplexed Shared lines Address valid or data valid control line Advantage - fewer lines Disadvantages More complex control Ultimate performance 2. Bus Arbitration ƒ More than one module controlling the bus ƒ e.g. CPU and DMA controller ƒ Only one module may control bus at one time ƒ Arbitration may be centralised or distributed 3. Centralised Arbitration ƒ Single hardware device controlling bus access Bus Controller Arbiter ƒ May be part of CPU or separate 4. Distributed ArbitrationEach module may claim the bus ƒ Control logic on all modules 5. Timing ƒ Co-ordination of events on bus
- 74. 73 ƒ Synchronous Events determined by clock signals Control Bus includes clock line A single 1-0 is a bus cycle All devices can read clock line Usually sync on leading edge Usually a single cycle for an event 6. Synchronous Timing Diagram
- 75. 74 7. Asynchronous Timing – Read Diagram 8. Asynchronous Timing – Write Diagram
- 76. 75 9. Examples PCI Bus • Peripheral Component Interconnection • Intel released to public domain • 32 or 64 bit • 50 lines 10. PCI Bus Lines (required) • Systems lines Including clock and reset • Address & Data 32 time mux lines for address/data Interrupt & validate lines • Interface Control • Arbitration Not shared Direct connection to PCI bus arbiter • Error lines 11. PCI Bus Lines (Optional) • Interrupt lines Not shared • Cache support • 64-bit Bus Extension Additional 32 lines Time multiplexed 2 lines to enable devices to agree to use 64-bit transfer • JTAG/Boundary Scan For testing procedures 12. PCI Commands • Transaction between initiator (master) and target • Master claims bus • Determine type of transaction e.g. I/O read/write • Address phase • One or more data phases
- 77. 76 13. PCI Read Timing Diagram 14. PCI Bus Arbitration
- 78. 77 References: Books Books 1. Computer Organization and Architecture By: William stallings (Preferred) 2. Computer System Architecture By: M.Morris Mano 3. Computer Architecture: A Quantitative Approach By: John L. Hennessy, David A. Patterson, David Goldberg 4. Computer Organization and Design Second Edition : The Hardware/Software Interface By : David Patterson, John Hennessy 5. Computer Architecture and Organisation By : J.P.Hayes 6. Digital Computer Design Principles By : M.R.Bhujade
- 79. 78 Lecture 8 INTERRUPTS & INSTRUCTION CYCLE Objectives of the Lecture 1. To understand INTERRUPTS and its role. 2. To understand importance of INTERRUPTS. 3. To understand INSTRUCTION CYCLE and its role. 4. To understand importance of INSTRUCTION CYCLE. Dear students let’s think of a everyday life scenario on the road. Suppose we are moving as per our normal routine following all traffic rules but all of a sudden cops restrict the whole traffic for a few minutes to give way to some very important person that means a person with high priority. The same scene takes place in computers as well when some high priority process comes and interrupts the running ones. These high priority processes are called Interrupts. Virtually all computers provide a mechanism by which other modules (I/O, memory) may interrupt the normal processing of the CPU. The table below lists the most common classes of interrupts. The specific nature of these interrupt is examined later. However, we need to introduce the concept now in order to understand more clearly the nature of the instruction cycle and the implications of interrupt on the interconnection structure. The reader need to be concerned at this stage about the details of the generation and processing of interrupt, but only focus on the communication between modules that results from interrupts. Interrupt are provided primarily as a way to improve processing efficiency. For example, most external devices are much slower than the processor. Suppose that the processor is transferring data to a printer using the instruction cycle scheme of Figure. After each write operation, the processor will have to pause and remain idle until the printer catches up. The length of this pause can be on the order of many hundreds or even thousands of instruction cycle that do not involve memory. Clearly this is a very wasteful use of the processor. With interrupts, the processor can be engage in executing other instructions while an I/O operation is in progress.
- 80. 79 TABLE: Classes of Interrupts ________________________________________________________________________ Program Generated by some condition that occurs as a result of an instruction execution, such as arithmetic overflow, division by zero, attempt to execute an illegal machine instruction, and reference outside a user’s allowed memory space. Timer Generated by a timer within the processor. This allows the operating system to perform certain function on a regular basis. I/O Generated by an I/O controller, to signal normal completion of an operation or to signal a variety of error conditions. Hardware failure Generated by a failure such as power failure or memory parity error As I already discussed concept of both instruction cycle and interrupts in the previous lectures , we will see them together now for a better understanding. The program to be executed consists of a set of instruction stored in memory. The central progressing unit (CPU) does the actual work by executing instruction specified in the program. In order to gain a greater understanding of this function and of the way in which the major components of the computer interact to execute a program, we need to look in more detail at the process of program execution. The simplest point of view is to consider instruction processing as consisting of two steps: The CPU reads (fetches) instructions from memory one at a time, and it executes each instruction. Program execution consists of repeating the process of instruction fetch and instruction execution. Of course the execution of an instruction may itself involve a number of steps. At this stage, we can justify the breakdown of instruction processing into the two stages of fetch and execution as follows: 1. The instruction fetch is a common operation for each instruction, and consists of reading an instruction from location in memory. 2. The instruction execution may involve several operations and depends on the nature of the instruction.
- 81. 80 The processing required for a single instruction is called an Instruction Cycle. Using the simplified two-steps description explained above, the instruction cycles is depicted The two steps are referred to as the Fetch Cycle and the Execute Cycle. Program execution halts only if the machine is turned off, some sort of unrecoverable error occurs, or a program instruction that halts the computer is encountered. INSTRUCTION CYCLE STATE DIAGRAM (without Interrupts)
- 82. 81 Interrupts and the Instruction Cycle With interrupt, the processor can be engaged in executing other instruction while an I/O Operation is in progress. Consider the flow of control in Figure below . As before, the user program reaches a point at which it makes a system call in the from of a WRITE call. The I/O program that invoked in this case consists only of the preparation code and the actual I/O command. After these few instructions have been executed, control returns to the user program. Meanwhile, the external device is busy accepting data from computer memory and printing it. This I/O operation is conducted concurrently with the execution of instruction in the user program. When the external device becomes ready to be serviced, that is, when it is ready to accept more data from the processor, the I/O module for that external device sends an interrupt request signal to the processor. The processor responds by suspending operation of the current program, branching off to a program to service that particular I/O device, known as an interrupt handler, and resuming the original execution after the device is serviced. From the point of view of the user program, an interrupt is just that: an interruption of the normal sequence of execution. When the interrupt processing is completed, execution resumes Thus, the user program does not have to contain any special code to accommodate interrupt; the processor and the operating system are responsible for suspending the user program and then resuming it at he same point. START Fetch Fetch Next Cycle Instruction HALT Execute Execute Instruction Cycle Interrupts Disabled Interrupts Enabled Check for Interrupt; Interrupt Process Cycle Interrupt FLOWCHART : Instruction cycle with interrupts
- 83. 82 THE Lecture IN A GO ! ! ! ! ! ! ! ! ! ! ! ! ! 1. Instruction Cycle • Two steps: Fetch Execute 2. Fetch Cycle • Program Counter (PC) holds address of next instruction to fetch • Processor fetches instruction from memory location pointed to by PC • Increment PC Unless told otherwise • Instruction loaded into Instruction Register (IR) • Processor interprets instruction and performs required actions 3. Execute Cycle • Processor-memory data transfer between CPU and main memory • Processor I/O Data transfer between CPU and I/O module • Data processing Some arithmetic or logical operation on data • Control Alteration of sequence of operations e.g. jump
- 84. 83 • Combination of above 4. Interrupt Cycle • Added to instruction cycle • Processor checks for interrupt Indicated by an interrupt signal • If no interrupt, fetch next instruction • If interrupt pending: Suspend execution of current program Save context Set PC to start address of interrupt handler routine Process interrupt Restore context and continue interrupted program 5. Transfer of Control via Interrupts
- 85. 84 6. Instruction Cycle with Interrupts 7. Program Timing Short I/O Wait
- 86. 85 8. Program Timing Long I/O Wait 9. Instruction Cycle (with Interrupts) - StateDiagram
- 87. 86 10. Multiple Interrupts • Disable interrupts Processor will ignore further interrupts whilst processing one interrupt Interrupts remain pending and are checked after first interrupt has been processed Interrupts handled in sequence as they occur 11. Define priorities Low priority interrupts can be interrupted by higher priority interrupts When higher priority interrupt has been processed, processor returns to previous interrupt 12. Multiple Interrupts – Sequential
- 88. 87 13. Multiple Interrupts – Nested 14. Time Sequence of Multiple Interrupts
- 89. 88 EXERCISE FOR U 1. Fetch cycle and memory read cycleare similar to a certain extent what is the difference between the two and why a fetch cycle is comprised of 4T states whereas MR cycle is comprised of 3T states. 2. Draw a StateDiagram of Instruction Cycle without Interrupts? 3. Draw a State Diagram of Instruction Cycle with Interrupts? 4. Draw a Diagram to explain Time Sequence of Multiple Interrupts? 5. Draw a Diagram to explain Transfer of Control via Interrupts. References: Books And Related Websites Books 1. Computer Organization and Architecture By: William stallings (Preferred) 2. Computer System Architecture By: M.Morris Mano 3. Computer Architecture: A Quantitative Approach By: John L. Hennessy, David A. Patterson, David Goldberg 4. Computer Organization and Design Second Edition : The Hardware/Software Interface By : David Patterson, John Hennessy 5. Computer Architecture and Organisation By : J.P.Hayes 6. Digital Computer Design Principles By : M.R.Bhujade
- 90. 89 Lecture 9 INTERNAL MEMORY Objectives of the Lecture 1. To understand INTERNAL MEMORY and its role. 2. To understand importance of its presence. 3. To understand its characteristics. As for human beings brain or rather memory is required to retain information or data, the same way computers also need memory.So, now I will discuss various types of memory and their characteristics. Broadly we classify memory in two categories: 1.Internal Memory 2.External Memory Today, I will discuss Internal memory with you. Before we go ahead let’s take a brief overview of characteristics of internal memory and understand these frequently used terms. TABLE : Key Characteristics of Computer Memory Systems Location Performance CPU Access time Internal (main) Cycle time External (secondary) Transfer rate Capacity Physical Type Word Semiconductor Number of words Magnetic surface Unit of Transfer Physical Characteristics Word Volatile/nonvolatile Block Erasable/nonerasable Access Method Organization Sequential access Direct access Random access Associative access
- 91. 90 • Word: The “natural” unit organization of memory. The size of the word is typically equal to the number of bits used to represent a number and to the instruction length. Unfortunately, there are many exceptions. For example, the CRAY-1 has a 64-bit word length but uses a 24-bit integer representation. The VAX has a stupendous variety of instruction lengths, expressed as multiples of bytes, and a word size of 32 bits. • Addressable Units: In many systems, the addressable unit is the word. However some system allow addressing at the byte level any case, the relationship between the length A of an address and the number N of addressable units is 2A = N. • Unit of Transfer: For main memory, this is the number of bits read out of or written into memory at a time. The unit of transfer need to equal a word or an addressable unit. For external memory. Data are often transferred in much larger units than a word, and these are referred to as blocks. One of the sharpest distinctions among memory types is the method of accessing units of data. Four types may be distinguished: • Sequential Access: Memory is organized into units of data, called records. Access must be made in a specific linear sequence. Stored addressing information is used to separate records and assist in the retrieval process. A process read / write mechanism is used, and this must be moved from its current location to the desired location, passing and rejecting each intermediate record. Thus, the time to access an arbitrary record is highly variable. • Direct Access: As with sequential access, direct access involves a shared read- write mechanism. However individual blocks or records have a unque address based on physical location. Access is accomplished by direct access to reach a general vicinity plus sequence searching, counting or waiting to reach the final location. Again, access time is variable. Desk units, discussed in Chapter 5, are direct access. • Random Access: Each addressable location in memory has a unique, physically wired-in addressing mechanism. The time to access a given location is independent of the sequence of prior access and is constant. Thus, any location can be selected at random and directly addressed and accessed. Main memory systems are random access. • Associative: This is a random – access type of memory that enables one to make a comparison of desired bit location within a word for a specified match, and to do this for all words simultaneously. Thus, a word is retrieved based on a portion of its contents rather than its address. As with ordinary random-access memory, each location had its own addressing mechanism, and retrieval time is constant independent of location or prior access patterns. Cache memories, discussed in Section 4.3 may employ associative access From a user’s point of view, the two most important characteristics of memory are capacity and performance. Three performance parameters are used: • Access Time: For random-access memory, this is the time it takes to perform a read to write operation, that is, the time from the instant that an address is presented to the memory to the instant that data have been stored or made available for use. For nonrandom-access memory, access time is the time it takes to position the read –write mechanism at the desired location • Memory Cycle Time: This concept is primarily applied to random – access memory and consists of the access time plus any additional time required before a second access can commence. This additional time may be required for transients to die out on signal lines or to regenerate data if they are read destructively.
- 92. 91 • Transfer Rate: This is the rate at which data can be transferred into or out of a memory unit. For random-access memory, it is equal to 1/(Cycle Time). For nonrandom-access memory, the following relationship holds: TN= TA + N R Where TN = Average time to read or write N bits TA = Average access time N = Number of bits R – Transfer rate, in bits second (bps) A variety of physical types of memory have been employed. The two most common today are semiconductor memory, using LSI or VLSI technology, and magnetic surface memory, used for disk and tape. Several physical characteristics of data storage are important. In a volatile memory, information decays naturally or is lost when electrical power is switched off. In a nonvolatile memory, information once recorded remains without deterioration until deliberately changed; no electrical power is needed to retain information. Magnetic-surface memories are nonvolatile. Semiconductor memory may be either volatile or nonvolatile. Nonerasable memory cannot be altered, expect by destroying the storage unit. Semiconductor memory of this type is known as read only memory (ROM). Of necessity, a practical nonerasable memory must also be nonvolatile. For random – access memory, the organization is key design issue. By organization is meant the physical arrangement of bits to form words. The obvious arrangement is not always used, as will be explained presently. Registers Cache Main Memory Magnetic Disk Magnetic Tape (a) Traditional Memory Hierarchy
- 93. 92 Registers Cache Main memory Disk Cache Magnetic Disk Magnetic Tape Optical Desk (b)Contemporary Memory Hierarchy FIGURE : The memory hierarchy SEMICONDUCTOR MAIN MEMORY In earlier computers, the most common form of random – access storage for computer main memory employed an array of doughnut-shaped ferromagnetic loops referred to as cores. Hence, main memory was often referred to as core, a term that persists to this day. The advent of, and advantages of, microelectronics has long since vanquished the magnetic core memory. Today, the use of semiconductor chips for main memory is almost universal. Key aspects of this technology are explored in this section. TABLE :Semiconductor Memory Types Category Erasure Write Mechanism Volatility Read-write Electrically Electrically Volatile Memory byte-level Read-only Not possible Masks memory UV light Block-level Nonvolatile Electrically, Electrically Read-mostly block-level memory Electrically, byte-level Memory Type Random-access Memory. (RAM) Read-only Memory. (ROM) Programmable ROM (PROM) Erasable PROM (EPROM) Flash memory Electrically Erasable PROM (EEPROM)
- 94. 93 THE Lecture IN A GO ! ! ! ! ! ! ! ! ! ! ! ! ! 1. Semiconductor Memory Types 2. Semiconductor Memory • RAM Misnamed as all semiconductor memory is random access Read/Write Volatile Temporary storage Static or dynamic 3. Memory Cell Operation
- 95. 94 4. Dynamic RAM • Bits stored as charge in capacitors • Charges leak • Need refreshing even when powered • Simpler construction • Smaller per bit • Less expensive • Need refresh circuits • Slower • Main memory • Essentially analogue Level of charge determines value 5. Dynamic RAM Structure 6. DRAM Operation
- 96. 95 • Address line active when bit read or written Transistor switch closed (current flows) • Write Voltage to bit line High for 1 low for 0 Then signal address line Transfers charge to capacitor • Read Address line selected transistor turns on Charge from capacitor fed via bit line to sense amplifier Compares with reference value to determine 0 or 1 Capacitor charge must be restored 7. Static RAM • Bits stored as on/off switches • No charges to leak • No refreshing needed when powered • More complex construction • Larger per bit • More expensive • Does not need refresh circuits • Faster • Cache • Digital Uses flip-flops
- 97. 96 8. Stating RAM Structure 9. Read Only Memory (ROM) • Permanent storage Nonvolatile • Microprogramming (see later) • Library subroutines • Systems programs (BIOS) • Function tables
- 98. 97 10. Types of ROM • Written during manufacture Very expensive for small runs • Programmable (once) PROM Needs special equipment to program • Read “mostly” Erasable Programmable (EPROM) Erased by UV Electrically Erasable (EEPROM) Takes much longer to write than read Flash memory Erase whole memory electrically 11. Organisation in detail • A 16Mbit chip can be organised as 1M of 16 bit words • A bit per chip system has 16 lots of 1Mbit chip with bit 1 of each word in chip 1 and so on • A 16Mbit chip can be organised as a 2048 x 2048 x 4bit array Reduces number of address pins Multiplex row address and column address 11 pins to address (211=2048) Adding one more pin doubles range of values so x4 capacity 12. Refreshing • Refresh circuit included on chip • Disable chip • Count through rows • Read & Write back • Takes time • Slows down apparent performance
- 99. 98 13. Error Correction • Hard Failure Permanent defect • Soft Error Random, non-destructive No permanent damage to memory • Detected using Hamming error correcting code 14. Error Correcting Code Function 15. Advanced DRAM Organization • Basic DRAM same since first RAM chips • Enhanced DRAM Contains small SRAM as well SRAM holds last line read (c.f. Cache!) • Cache DRAM Larger SRAM component Use as cache or serial buffer
- 100. 99 16. Synchronous DRAM (SDRAM) • Access is synchronized with an external clock • Address is presented to RAM • RAM finds data (CPU waits in conventional DRAM) • Since SDRAM moves data in time with system clock, CPU knows when data will be ready • CPU does not have to wait, it can do something else • Burst mode allows SDRAM to set up stream of data and fire it out in block • DDR-SDRAM sends data twice per clock cycle (leading & trailing edge) 17. SDRAM Operation 18. RAMBUS • Adopted by Intel for Pentium & Itanium • Main competitor to SDRAM • Vertical package – all pins on one side • Data exchange over 28 wires < cm long • Bus addresses up to 320 RDRAM chips at 1.6Gbps • Asynchronous block protocol 480ns access time Then 1.6 Gbps
- 101. 100 19. RAMBUS Diagram EXERCISE FOR U 1 A designer wants to use hard disk as main memory instead of semiconductor memory. This idea can be easily rejected since the hard disk is a sequential access memory, however if we accept a large access time, is it possible to build a RAM around the hard disk with, necessary hardware and/or software so that it can be used atleast for experimental purposes. How? 2 The SRAM is more reliable than DRAM but costlier than DRAM. One designer wanted to use SRAM for the OS area and DRAM for user program area. Identify the problems that will be caused if this idea is accepted. 3 The flash memory is widely used instead of hard disk, in portable PC’s such as notebooks, in order to reduce weight an increase ruggedness. Why is not applicable in desktop computers and server systems.
- 102. 101 References: Books Books 1 Computer Organization and Architecture By: William stallings (Preferred) 2 Computer System Architecture By: M.Morris Mano 3 Computer Architecture: A Quantitative Approach By: John L. Hennessy, David A. Patterson, David Goldberg 4 Computer Organization and Design Second Edition : The Hardware/Software Interface By : David Patterson, John Hennessy 5 Computer Architecture and Organisation By : J.P.Hayes 6 Digital Computer Design Principles By : M.R.Bhujade
- 103. 102 Lecture 10 INPUT / OUTPUT Objectives of the Lecture 1. To understand INPUT / OUTPUT and its role. 2. To understand its characteristics. Dear students this is very important for you to know that In addition to the CPU and a set of memory modules, the third key element of a computer system is a set of I/O modules. Each modules interface to the system bus or central switch and controls one or more peripheral devices. An I/O module is not simply mechanical connectors that wire a device into the system bus. Rather, the I/O module contains some,” that is, it contains logic for performing a communication function between the peripheral and the bus. The reader may wonder why one does not connect peripherals directly to the system bus. The reasons are • There are a wide variety of peripherals with various methods of operation. It would be impractical to incorporate the necessary logic within the CPU to control a range of devices. • The data transfer rate of peripherals is often much slower than that of the memory or CPU. Thus, it is impractical to use the high-speed system bus to communication directly with a peripheral. • Peripherals often use different data formats and word lengths than the computer to which they are attached. Thus, an I/O module is required. This modules has two major functions . • Interface to the CPU and memory via the system bud or central switch. • Interface to one or more peripheral devices by tailored data links. We begin this chapter with a brief discussion of external devices, followed by an overview of the structure and function can be performed in cooperation with the CPU and memory the internal I/O interface. Finally, the external I/O interface, between the I/O module and the outside world, is examined. EXTERNAL DEVICES A computer system is of no use without some means of input and output. I/O operations are accomplished through a wide assortment of external devices that provide a means of exchanging data between the external environment and the computer. An external device attaches to the computer by a link to an I/O module The link is used to exchange control, status, and data
- 104. 103 between the I/O module and the external device. An external device connected to an I/O module is often referred to as a peripheral device or, simply, a peripheral. Address Lines Data lines System Bus Control Lines I/O module FIGURE 6.2 An external device Links to Peripheral Devices FIGURE : An external device We can broadly classify external devices into three categories: • Human-Readable: Suitable for communicating with the computer user. • Machine-Readable: Suitable for communicating with equipment. • Communication: Suitable for communicating with remote devices. Example of human-readable devices is video display terminals (VDTs) and printers. Examples of machine-readable devices are magnetic disk and tape systems, and sensors and actuators, such as are used in a robotics application. Note that we are viewing disk and tape systems as I/O devices in this chapter, whereas in previous lecture we viewed them as memory devices. From a functional point of view, these devices are part of the memory hierarchy, and their use is appropriately discussed in previous chapter. From a structural point of view, these devices are controlled by I/O modules and are hence to be considered in this lecture. Communication devices allow a computer to exchange data a with remote device, which may be a human-readable device, such as a terminal, a machine-readable device, or even another computer.
- 105. 104 Control form Status to Data (bits) to and from I/O Module I/O Module I/O Module Buffer Control Logic Transducer Data (Device-unique) to and from Environment An external device Keyboard/Monitor The most common means of computer/ user interaction is a keyboard/monitor arrangement. The user provides input through the keyboard. This input is then transmitted to the computer and may also be displayed on the monitor. In addition, the monitor displays data provided by the computer. The basic unit of exchange is the character. Associated with each character is a code, typically 7 or 8 bits in length. The most commonly used code is a 7-bit code referred to as ASCII (American Standard Code for Information Interchange) in the United States and CCITI Alphabet Number 5 internationally. Each character in this code is represented by a unique 7- bit binary code; thus, 128 different characters can be represented. Table below lists all of the code values. In the table, the bits of each character are labeled fromb7, which is the most significant bit, to b1, the least significant bit. Characters are of two types: printable and control. Printable characters are the alphabetic, numeric, and special characters that cab be printed on paper or displayed on a screen. For example. The bit representation of the character ”K” is 1001011. Some of the control characters have to do with controlling the printing or displaying of characters; an example is carriage return. Other control characters are concerned with communications procedures. For keyboard input, when a key is depressed by the user, this generators an electronic signal that is interpreted by the transducer in the keyboard and translated into the bit pattern of the corresponding ASCII code. This is pattern is then transmitted to the I/O module in the computer. At the computer, the text can be stored in the same ASCII code. On output, ASCII code characters are transmitted to an external device from the I/O module. The transducer at the
- 106. 105 device interprets this code and sends the required electronic signals to the device to either display the indicated character or perform the requested control function. I/O MODULES Module Function An I/O modules is the entity within a computer responsible for the control of one or more external devices and for the exchange of data between those devices and main memory and / or CPU registers. Thus, the I/O module must have an interface to the computer (to the CPU and main memory) and an interface internal to the computer (to the external device). The major functions or requirements for an I/O module fall into the following categories: • Control and Timing • CPU Communication • Device Communication • Data Buffering • Error Detection During any period of time, the CPU may communication with one or more external devices in unpredictable patterns, depending on the program’s need for I/O. The internal resources, such as main memory and the system bus, must be shared among a number of activities including data I/O. Thus, the I/O function includes a control and timing requirement, to coordinate the flow of traffic between internal resources and external devices. For example the control of the transfer of data from an external device to the CPU might involve the following sequence of steps: 1. The CPU interrogates the I/O module to check the status of the attached device. 2. The I/O module returns the device status. 3. If the device is operational and ready to transmit, the CPU requests the transfer of data, by means of a command to the I/O module. 4. The I/O module obtains a unit of data (e.g., 8 or 16bits) from the external device. 5. The data are transferred from the I/O module to the CPU. If the system employs a bus, then each of the interactions between the CPU and the I/O module involves one or more bus arbitrations. The preceding simplified scenario also illustrates that the I/O module must have the capacity to engage in communication with the CPU and with the external device. CPU communication involves. • Reported with a status signal. Common status signals are BUSY and READY. There may also be signals to report various error conditions. • Address Recognition: Just as each word of memory has an address, so does each I/O device. Thus, an I/O module must recognize one unique address for each peripheral it controls.
- 107. 106 On the other side, the I/O module must be able to perform device communication. This communication involves commands, status information, and data . • An essential task of an I/O module is data buffering. The need for this function is apparent from Table. Whereas the transfer rate into Command Decoding: The I/O module accepts commands from the CPU. These commands are generally sent as signals on the control bus. For example, an I/O module for a disk drive might accept the following commands: READ SECTOR, WRITE SECTOR, SEEK track number, and SCAN record ID. The latter two commands each include a parameter that is sent on the data bus. • Data: Data are exchanged between the CPU and the I/O module over the data bus. Status Reporting: Because peripherals are so slow, it is important to know the status of the I/o module. For example, if an I/O module is asked to send data to the CPU (read), it many not be ready to do so because it is still working on the previous I/O command. This fact can be and out of main memory or the CPU is quite high, the rate is orders of magnitude lower for most peripheral devices. Data coming from main memory are sent to an I/O module in rapid burst. The data are buffered in the I/O module and then sent to the peripheral device at its data rate. In the TABLE : Examples of I/O Devices Categorized by Behavior, Partner, and Data Rate (HENN90) Data Rate Device Behavior Partner (Kbytes/sec) Keyboard Input Human 0.01 Mouse Input Human 0.02 Voice input Input Human 0.02 Scanner Input Human 200 Voice Output Output Human 0.6 Line printer Output Human 1 Laser printer Output Human 100 Graphics display Output Human 30,000 CPU to frame buffer Output Human 200 Network-terminal Input or output Human 0.05 Network-LAN Input or Output Human 200 Optical disk Storage Human 500 Magnetic tape Storage Human 2,000 Magnetic disk Storage Human 2,000 Opposite direction, data are buffered so as not to tie up the memory in a slow transfer operation. Thus, the I/O module must be able to operate at both device and memory speeds. Finally, an I/O module is often responsible for error detection and for subsequently reporting errors to the CPU. One class of errors includes mechanical and electrical malfunctions reported
- 108. 107 by the device (e.g., paper jam, bad disk track).Another class consists of unintentional changes to the bit pattern as it is transmitted from device to I/O module. Some form of error-detecting code is often used to detect transmission errors. A common example is the use of a parity bit on each character of data. For example, the ASCII character code occupies 7 bits of a byte. The eighth bit is set so that total number of “one”s in the byte is even (even parity) or odd (odd parity). When a byte is received, the I/O module checks the parity to determine whether an error has occurred. THE Lecture IN A GO ! ! ! ! ! ! ! ! ! ! ! ! ! 1 Input/Output Problems Wide variety of peripherals Delivering different amounts of data At different speeds In different formats All slower than CPU and RAM Need I/O modules 2 Input/Output Module Interface to CPU and Memory Interface to one or more peripherals 3 Generic Model of I/O Module 4 External Devices • Human readable
- 109. 108 Screen, printer, keyboard • Machine readable Monitoring and control • Communication Modem Network Interface Card (NIC) 5 External Device Block Diagram
- 110. 109 6. Typical I/O Data Rates • I/O Module Function • Control & Timing • CPU Communication • Device Communication • Data Buffering • Error Detection • I/O Steps • CPU checks I/O module device status • I/O module returns status • If ready, CPU requests data transfer • I/O module gets data from device • I/O module transfers data to CPU • Variations for output, DMA, etc.
- 111. 110 • I/O Module Diagram • I/O Module Decisions • Hide or reveal device properties to CPU • Support multiple or single device • Control device functions or leave for CPU • Also O/S decisions e.g. Unix treats everything it can as a file References: Books Books 1 Computer Organization and Architecture By: William stallings (Preferred) 2 Computer System Architecture By: M.Morris Mano
- 112. 111 3 Computer Architecture: A Quantitative Approach By: John L. Hennessy, David A. Patterson, David Goldberg 4 Computer Organization and Design Second Edition : The Hardware/Software Interface By: David Patterson, John Hennessy 5 Computer Architecture and Organisation By : J.P.Hayes 6 Digital Computer Design Principles By : M.R.Bhujade
- 113. 112 Lecture 11 INPUT / OUTPUT (CONTD.) Objectives of the Lecture 1. To understand INPUT / OUTPUT Techniques 2. To understand its characteristics and importance. Let us see today that what are the different methods being followed for smoothened input / output.There are three types of I / O Techniques being followed which have their own advantages and disadvantages.The three types of I / O Techniques are as follws: 1. PROGRAMMED I/O 2. INTERRUPT-DRIVEN I/O 3. DIRECT MEMORY ACCESS Lets discuss each of them one by one. PROGRAMMED I/O: Three techniques are possible for I/O operations. With programmed I/O, data Are exchanged between the CPU and the I/O module. The CPU executes a program that gives it direct control of the I/O operation, including sensing device status, sending a read or write command, and transferring the data. When the CPU issues a command to the I/O module, this is wasteful of CPU time. With interrupt-driven I/O, the CPU issues an I/O command, contains to execute other instructions, and is interrupted by the I/O module when the latter has completed its work. With both programmed and interrupt I/O, the CPU is responsible for extracting data from main memory for output and storing data in main memory for input. The alternative is known as direct memory access (DMA). In this mode, the I/O module and main memory exchange data directly, without CPU involvement. INTERRUPT-DRIVEN I/O: The problem with programmed I/O is that the CPU has to wait a long time for the I/O module of concern to be ready for either reception or transmission of data. The CPU while waiting must repeatedly interrogate the status of the I/O module. As a result, the level of the performance of the entire system is severely degraded. An alternative is for the CPU to issue an I/O command to a module and then go on to do some other useful work. The I/O module will then interrupt the CPU to request service when it is ready
- 114. 113 to exchange data with the CPU. The CPU then executes the data transfer, as before and then resumes its former processing. Let us consider how this works, first form the point of view of the I/O module. For input, the I/O module receives a READ command from the CPU. The I/O module then proceeds to read data inform an associated peripheral. Once the data are in the module’s data register, the module signals an interrupt to the CPU over a control line. The module the waits until its data are requested by the CPU. When the request is made, the module places its data on the data bus and is then ready for another I/O operation. From the CPU’s point of view, the action for input is as follows. The CPU issues a READ command. It then goes off and does something else (e.g., the CPU may be working on several different programs at the same time). At the end of each instruction cycle, the CPU checks for interrupts .When the interrupt from the I/O module occurs, the CPU saves the context (e.g., program counter and CPU registers) of the current program and processes the interrupt. In this case, the CPU reads the word of data from the I/O module and stores it in memory. It then restores the context of the program it was working on (or some other program) and resumes execution.
- 115. 114 FIGURE:SIMPLE INTERRUPT PROCESSING Device Controller or Other System Hardware Issues an Interrupt Processor Finishes Execution of Current Instruction Processor Signals Acknowledgement of Interrupt Processor Pushes PSW and PC onto Control Stack Processor Loads New PC Value Based on Interrupt Save Remainder of Process state Information Process interrupt Restore Progress State Information Restore OLD PSW and PC Hardwar Software Device Controller or Other System Hardware Issues an Interrupt Processor Finishes Execution of Current Instruction Hardwar
- 116. 115 DIRECT MEMORY ACCESS: Drawbacks of Programmed and Interrupt-Driven I/O Interrupt-driven I/O, though more efficient than simple programmed I/O. still requires the active intervention of the CPU to transfer data between memory and an I/O module, and any data transfer must traverse a path through the CPU. Thus, both these forms of I/O suffer from two inherent drawbacks: 1. The I/O transfer rate is limited by the speed with which the CPU can test and service a device. 2. The CPU is tied up in managing an I/O transfer; a number of instructions must be executed for each I/O transfer . There is somewhat of a trade-off between these two drawbacks. Consider the transfer of a block of data. Using simple programmed I/O, the CPU is dedicated to the task of I/O and can move data at a rather high rate, at the cost of doing nothing else. Interrupt I/O frees up the CPU to some extant at the expense of I/O activity and I/O transfer rate. When large volumes of data are to be moved, a more efficient technique is required: direct memory access (DMA). The figure below gives a comparison of all the types of I/O.
- 117. 116 INTERRUPT I/O PROGRAMMED I/O Issue Read Command to I/O Module Read Status of I/O Module Chec k Statu Read World from I/O Module Write World into Memory Done Issue Read Command to I/O Module Read Status of I/O Module Check Status Read Word from I/O Module Write World into Memory Done CPU I/O I/O CPU Error Condition I/O CPU CPU Memory Next Instruction CPU I/O Do Something Else Interrupt I/O CPU Error condition Ready I/O CPU CPU Memory Next Instruction
- 118. 117 DIRECT MEMORY ACCESS DMA function DMA involves an additional module on the system bus. The DMA module is capable of mimicking the CPU and, indeed, of taking over control of the system from the CPU. The technique works as follows. When the CPU wishes to read or write a block of data, it issues a command to the DMA module, by sending to the DMA module the following information: • Whether a read or write is requested. • The address of the I/O device involved. • The starting location in memory to read form or write to. • The number of words to be read or written. The CPU then continues with other work. It has delegated this I/O operation to the DMA module, and that module will take care of it. The DMA module transfers the entire block of data, one word at a time, directly to or from memory, without going through the CPU. When the transfer is complete, the DMA modules send an interrupt signal to the CPU. Thus, the CPU is involved only at the beginning and end of the transfer. The DMA module needs to take control of the bus in order to tranfer data to and from memory. For this purpose, the DMA module must use the bus only when the CPU does not need it, or it must force the CPU to temporarily suspend operation. The latter technique is more common and is referred to as cycle stealing since the DMA module in effect steals a bus cycle. The Figure shows where in the instruction cycle the CPU may be suspended. In each case, the CPU is suspended just before it needs to use the bus. The DMA module then transfers one word and returns control to the Issue Read Block Command to DMA Module Read Status of DMA Module CPU DMA Do Something Else Interrupt
- 119. 118 CPU. Note that this is not an interrupt; the CPU does not save a context and do something else. Rather, the CPU pauses for one bus cycle. The overall effect is to cause the CPU to execute more slowly. Nevertheless, for a multiple-word I/O transfer, DMA is far more efficient than interrupt – driven or programmed I/O. Data Lines Address Lines DMA REQ FIGURE:TYPICAL DMA BLOCK DIAGRAM FIGURE:DMA AND INTERRUPT BREAKPOINTS DURRING AN INSTRUCTION CYCLE Data Count Data Register Address Register Control Logic DMA ACK INTR Read Write Processor Cycle Processor Cycle Processor Cycle Processor Cycle Processor Cycle Fetch Instruction Decode Instruction Fetch Operand Execute Instruction Store Result Interrupt Breakpoint DMA Breakpoints INSTRUCTION CYCLE
- 120. 119 THE Lecture IN A GO ! ! ! ! ! ! ! ! ! ! ! ! ! 1 Input Output Techniques • Programmed • Interrupt driven • Direct Memory Access (DMA) 2 Programmed I/O • CPU has direct control over I/O Sensing status Read/write commands Transferring data • CPU waits for I/O module to complete operation • Wastes CPU time 3 Programmed I/O – detail • CPU requests I/O operation • I/O module performs operation • I/O module sets status bits • CPU checks status bits periodically • •I/O module does not inform CPU directly • I/O module does not interrupt CPU • CPU may wait or come back later 4 I/O Commands • CPU issues address Identifies module (& device if >1 per module) • CPU issues command Control - telling module what to do e.g. spin up disk Test - check status e.g. power? Error? Read/Write Module transfers data via buffer from/to device
- 121. 120 5 Addressing I/O Devices • Under programmed I/O data transfer is very like memory access (CPU viewpoint) • Each device given unique identifier • CPU commands contain identifier (address) 6 I/O Mapping • Memory mapped I/O Devices and memory share an address space I/O looks just like memory read/write No special commands for I/O Large selection of memory access commands available • Isolated I/O Separate address spaces Need I/O or memory select lines Special commands for I/O Limited set 7 Interrupt Driven I/O • Overcomes CPU waiting • No repeated CPU checking of device • I/O module interrupts when ready 8 Interrupt Driven I/O Basic Operation • CPU issues read command • I/O module gets data from peripheral whilst CPU does other work • I/O module interrupts CPU • CPU requests data • I/O module transfers data 9 CPU Viewpoint • Issue read command • Do other work • Check for interrupt at end of each instruction cycle • If interrupted:- Save context (registers) Process interrupt
- 122. 121 Fetch data & store • See Operating Systems notes 10 Design Issues • How do you identify the module issuing the interrupt? • How do you deal with multiple interrupts? i.e. an interrupt handler being interrupted 11 Identifying Interrupting Module (1) • Different line for each module PC Limits number of devices • Software poll CPU asks each module in turn Slow 12 Identifying Interrupting Module (2) • Daisy Chain or Hardware poll Interrupt Acknowledge sent down a chain Module responsible places vector on bus CPU uses vector to identify handler routine • Bus Master Module must claim the bus before it can raise interrupt e.g. PCI & SCSI 13 Multiple Interrupts • Each interrupt line has a priority • Higher priority lines can interrupt lower priority lines • If bus mastering only current master can interrupt 14 Example - PC Bus • 80x86 has one interrupt line • 8086 based systems use one 8259A interrupt controller • 8259A has 8 interrupt lines
- 123. 122 15 Sequence of Events • 8259A accepts interrupts • 8259A determines priority • 8259A signals 8086 (raises INTR line) • CPU Acknowledges • 8259A puts correct vector on data bus • CPU processes interrupt 16 ISA Bus Interrupt System • ISA bus chains two 8259As together • Link is via interrupt 2 • Gives 15 lines 16 lines less one for link • IRQ 9 is used to re-route anything trying to use IRQ 2 Backwards compatibility • Incorporated in chip set 82C59A Interrupt Controller
- 124. 123 17. Direct Memory Access • Interrupt driven and programmed I/O require active CPU intervention Transfer rate is limited CPU is tied up • DMA is the answer • 20.DMA Function • Additional Module (hardware) on bus • DMA controller takes over from CPU for I/O 18 DMA Module Diagram 19 DMA Operation • CPU tells DMA controller:-
- 125. 124 Read/Write Device address Starting address of memory block for data Amount of data to be transferred • CPU carries on with other work • DMA controller deals with transfer • DMA controller sends interrupt when finished • 23.DMA Transfer Cycle Stealing • DMA controller takes over bus for a cycle • Transfer of one word of data • Not an interrupt CPU does not switch context • CPU suspended just before it accesses bus i.e. before an operand or data fetch or a data write • Slows down CPU but not as much as CPU doing transfer 24. Aside • What effect does caching memory have on DMA? • Hint: how much are the system buses available? 20 DMA Configurations (1) • Single Bus, Detached DMA controller • Each transfer uses bus twice I/O to DMA then DMA to memory • CPU is suspended twice 21 DMA Configurations (2) • Single Bus, Integrated DMA controller • Controller may support >1 device • Each transfer uses bus once DMA to memory • CPU is suspended once
- 126. 125 22 DMA Configurations (3) • Separate I/O Bus • Bus supports all DMA enabled devices • Each transfer uses bus once DMA to memory • CPU is suspended once
- 127. 126 EXERCISE FOR U 1. A student is working on his processor he wants to do two jobs simultaneously one is, he wants to do certain computational functions and the second is he wants to transfer data to peripheral device. How will he achieve this. 2. Enlist each and every change which is incorporated inside the processor once an interrupt is activated during the normal execution of program References: Books Books 1 Computer Organization and Architecture By: William stallings (Preferred) 2 Computer System Architecture By: M.Morris Mano 3 Computer Architecture: A Quantitative Approach By: John L. Hennessy, David A. Patterson, David Goldberg 4 Computer Organization and Design Second Edition : The Hardware/Software Interface By : David Patterson, John Hennessy 5 Computer Architecture and Organisation By : J.P.Hayes 6 Digital Computer Design Principles By : M.R.Bhujade
- 128. 127 Lecture 12 INTRODUCTION TO CPU Objectives of the lecture: 1.This will introduce you all to the brain of the computer ie CPU. Hello students! Today I would introduce you all to the very important part of the computer ie the central peripheral unit,and also the arithmetic and logic unit. The central processing unit (CPU) is the 'brain' of the computer, where the calculations are carried out. A CPU has an Arithmetic/Logic Unit (ALU), which does arithmetic and logic calculations, and a number of registers, which are used to temporarily store data to be used in calculations. The central processing unit (CPU) is the part of a computer that interprets and carries out the instructions contained in the software. In most CPUs, this task is divided between a control unit that directs program flow and one or more execution units that perform operations on data. Almost always, a collection of registers is included to hold operands and intermediate results. The term CPU is often used vaguely to include other centrally important parts of a computer such as caches and input/output controllers, especially in computers with modern microprocessor chips that include several of these functions in one physical integrated circuit. Manufacturers and retailers of desktop computers often erroneously describe the computer case and its contents as the CPU which is misleading. A family of CPU designs is often referred to as a CPU architecture. Notable CPU architectures include: • Intel's x86 architecture • Zilog's architecture • IBM's System/360 architecture • DEC's PDP-11 architecture, and its successor, the VAX architecture • Motorola's 68000 architecture • Sun Microsystems's SPARC architecture • MIPS Computer Systems Inc.'s MIPS architecture • HP's PA-RISC architecture • DEC's Alpha architecture • The AIM Alliance's PowerPC architecture • DEC and Acorn ARM's StrongARM architecture • SuperH's SuperH architecture • UNIVAC 1100/2200 series architecture (currently supported by Unisys ClearPath IX computers) • 1750A, the U.S.'s military standard computer. • AP-101, the space shuttle's computer
- 129. 128 The above processor architectures could also be characterized by their CPU design like register size. Today most desktop computers have 32-bit processors; 64-bit processors are being phased in. Smaller devices like mobile phones, PDAs, or portable video game devices may have 16 or 8-bit processors. Arithmetic and logical unit An arithmetic and logical unit (ALU) is one of the core components of all central processing units. It is capable of calculating the results of a wide variety of common computations. The most common available operations are the integer arithmetic operations of addition, subtraction, and multiplication, the bitwise logic operations of AND, NOT, OR, and XOR, and various shift operations. Typically, a standard ALU does not handle integer division nor any floating point operations. For these calculations a separate component, such as a divider or floating point unit (FPU), is often used, although it is also possible that a microcode program may use the ALU to emulate these operations. The ALU takes as inputs the data to be operated on and a code from the control unit indicating which operation to perform, and for output provides the result of the computation. In some designs it may also take as input and output a set of condition codes, which can be used to indicate cases such as carry-in or carry-out, overflow, or other statuses. Let us see some of the operations which are performed with the help of ALU. The arithmetic and logic unit (ALU) is that part of the computer that actually performs arithmetic and logical operations on data. All of the other elements of the computer system—control unit, registers, memory, I/O—are there mainly to bring data into the ALU for it to process and then to take the results back out. We have, in a sense, reached the core or essence of a computer when we consider the ALU. An arithmetic and logic unit and, indeed, all electronic components in the computer are based on the use of simple digital logic devices that can store binary digits and perform simple Boolean logic operations. Full fig indicates, in very general terms, how the ALU is interconnected with the rest of the CPU. Data are presented to the ALU in registers, and the results of an operation are stored in registers. These registers are temporary storage locations within the CPU that are connected by signal paths to the ALU (e.g., see Figure 12.1). The ALU will also set flags as the result of an operation. For example, an overflow flag is set to 1 if the result of a computation exceeds the length of the register into which it is to be stored. The flag values are also stored in registers within the CPU. The control unit provides signals that control the operation of the ALU, and the movement of the data into and out of the ALU.
- 130. 129 FIGURE 12.1 ALU Inputs and Outputs INTEGER REPRESENTATION In the binary number system , arbitrary numbers can be represented with just the digits 0 and 1, the minus sign, and the period. For example: -1101.01012 = -11.312510 For purposes of computer storage and processing, however, we do not have the benefit of minus signs and periods. Only binary digits (0 and 1) may be used to represent numbers. If we only used nonnegative integers, the representation is straightforward. An 8-bit word could be used to represent the numbers from 0 to 255. For example: 00000000 = 0 00000001 = 1 00101001 = 41 10000000 = 128 11111111 = 255 In general, if an n-bit sequence of binary digits an - 1an – 2 … A1a0 is interpreted as an unsigned integer A, its value is n-1 A=Σ 2i ai I=0 Sign-Magnitude Representation The use of unsigned integers is insufficient in the many cases when we need to represent negative as well as positive integers. The are several other conventions we could use for this. All ALU Flags Registers Registers Control Unit
- 131. 130 of them involve treating the most significant (leftmost) bit in the word as a sign bit: If the l;eftmost bit is 0, the number is positive, and if the leftmost bit is 1, the number is negative. The simplest form of representation that employs a sign bit is the sing-magnitude representation. In an n-bit word, the rightmost n – 1 bits hold the magnitude of the integer. For example: +18 = 00010010 -18 = 10010010 (sign-magnitude) There are several drawbacks to sign-magnitude representation. One is that addition and subtraction require consideration of both the signs of the numbers and their relative magnitudes in order to carry out the required operation. This should become clear in the discussion in Section 8.3. Another drawback is that there are two representations of 0: +010 = 00000000 -010 = 10000000 (sign-magnitude) This is inconvenient, because it is slightly more difficult to test for 0 (an operation performed frequently by computers) than if there were a single representation. Two’s Complement Representation 1 The two’s complement representation was developed to overcome the two principal drawbacks of the sign-magnitude representation: addition and subtraction in sign-magnitude are inefficient, and there are two representations for zero. Like sign-magnitude, two’s complement representation uses the most significant bit as a sign bit, making it easy to test whether an integer is positive or negative. It differs from sign-magnitude representation in the way that the other bits are interpreted. Two’s complement representation is best understood by defining it in terms of a weighted sum of bits, as we did above for unsigned and sign-magnitude representations. Consider an n-bit integer, A, in two’s complement representation. If A is positive, then the sign bit, an-1, is zero. The remaining bits represent the magnitude of the number in the same fashion as for sign-magnitude; thus, n-2 A = Σ2i ai for A> 0. I=0
- 132. 131 The number zero is identified as positive and therefore has a 0 sign bit and a magnitude of all 0s. We can see that the range of positive integers that may be represented is from 0 (all of the magnitude bits are 0) through 2n-1 – 1 (all of the magnitude bits are 1). Any larger number would require more bits. Now, for a negative number A, the sign bit, an-1, is 1. The remaining n-1 bits can take on any one of 2n-1 values. Therefore, the range of negative integers that can be represented is from –1 to –2n- 1. It turns out that a convenient assignment of values is to let the bits an – 1an-2 …. a1a0 be equal to the positive number 2n-1 + A, as obtained by n-2 n-2 2n-1 + A = Σ2i ai, so that A + -2n-1 + Σ 2i ai I=0 I=0 Since the sign bit is 1, we can write the expression for the negative number as n-2 A = 2n-1 an-1 + Σ2i ai I=0 In the case of positive integers, an-1 = 0, and so the term –2n-1 an-1 = 0. Therefore, Equation 9-1 defines the two’s complement representation for both positive and negative numbers. Table 8.1 compares the sign-magnitude and two’s complement representations for 4-bit integers. Although two’s complement is an awkward representation from the human point of view, we will se that it facilitates the most important arithmetic operations, addition and subtraction. For this reason, it is almost universally used as the processor representation for integers. A useful illustration of the nature of two’s complement representation is a value box, in which the value on the far right in the box is 1 (20 ) and each succeeding position to the left is double in value, until the leftmost position, which is negated. As you can see in Figure 8.2a, the most negative two’s complement number that
- 133. 132 TABLE 8.1 Comparison of Sign-Magnitude and Two’s-Complement Representation for 4-bit integers Decimal Sign-Magnitude Two’s-Complement Representation Representation Representation +7 0111 0111 +6 0110 0110 +5 0101 0101 +4 0100 0100 +3 0011 0011 +2 0010 0010 +1 0001 0010 +0 0000 0000 -0 1000 ----- -1 1001 1111 -2 1010 1110 -3 1011 1011 -4 1100 1100 -5 1101 1011 -6 1110 1010 -7 1111 1001 -8 1111 1000 -128 64 32 16 8 4 2 1 (a) An Eight-Position Two’s Complement Value Box -128 64 32 16 8 4 2 1 0 0 0 0 0 0 0 0 (b) Convert Binary 10000011 to Decimal
- 134. 133 -128 64 32 16 8 4 2 1 1 0 0 0 1 0 0 0 (c) Convert Decimal – 120 to Binary Fig. Use of a Value Box for Conversion Between Two’s Complement Binary and decimal Can be represented is –2n-1; if any of the bits other than those sign bit is 1, it adds a positive amount to the number. Also, it is clear that a negative number must have a 1 at its leftmost position and a positive number must have a 0 in that position. Thus, the largest positive number is a 0 followed by all 1s, which equals 2n-1 – 1. The remainder of Figure 8.2 illustrates the use of the value box to convert from two’s complement to decimal, and from decimal to two’s complement. Converting Between Different Bit Lengths It is sometimes desirable to take an n-bit integer and store it in m bits, where m>n. In sign- magnitude notation, this is easily accomplished: simply move the sign bit to the new leftmost position and fill in with zeros. For Example: +18 = 00010010 (sign-magnitude, 8 bits) +18 = 0000000000010010 (sign-magnitude, 16 bits) -18 = 10010010 (sign-magnitude, 8 bits) -18 = 1000000000010010 (sign-magnitude, 16 bits) This procedure will not work for two’s complement negative integers. Using the same example: +18 = 00010010 (two's complement, 8 bits) +18 = 0000000000010010 (two's complement,16 bits) -18 = 10010010 (two's complement, 8 bits) -65,518 = 1000000000010010 (two's complement, 16 bits)
- 135. 134 Instead, the rule for two’s complement integers is to move the sign bit to the new leftmost position and fill in with copies of the sign bit. For positive numbers, fill in with 0s, and for negative numbers, fill in with 1s. Thus, we have +18 = 0000000000010010 (two's complement, 8 bits) -18 = 10010010 (two's complement, 16 bits) To see why this rule works, let us again consider an n-bit sequence of binary digits an-1an-2 …. A1a0 interpreted as a two’s complement integer A, so that its value is n-2 A = -2n-1- an-1 + Σ2i ai I=0 If A is a positive number, the rule clearly works. Now, suppose A is negative and we wanto construct an m-bit representation, with m> n. Then m-2 A = -2m-1- am-1 + Σ2i ai I=0 Two The values must be equal: m-2 n-2 A = -2m-1- + Σ2i ai = -2n-1 +Σ2i ai I=0 I=0 m-2 A = -2m-1- + Σ2i ai = -2n-1 I=n-1 m-2 A = -2m-1- + Σ2i ai = -2nm1 I=n-1 n-2 m-2 n-2 1 + Σ2i + Σ2i ai 1 + Σ2i I=0 I=n-1 I=0
- 136. 135 m-2 m-2 Σ 2i ai = Σ 2i I=n-1 I=n-1 In going from the first to the second equation, we require that the least significant n-1 bits do not change between the two representations. Then, we get to the final equation, which is only true if all of the bits in positions n-1 through m-2 are 1. Thus, the rule works. Fixed-Point Representation Finally, we mention that the representations discussed in this section are sometimes referred to as fixed point. This is because the radix point (binary point) is fixed and assumed to be to the right of the rightmost digit. The programmer can use the same representation for binary fractions by scaling the numbers so that the binary point is implicitly positioned at some other location. INTEGER ARITHMETIC This section examines common arithmetic function on numbers in two’s complement representation. Negation In sign-magnitude representation, the rule for forming the negation of an integer is simple: invert the sign bit. In two’s complement notation, the negation of an integer can be formed using the following rules: 1. Take the Boolean complement of each bit of the integer (including the sign bit). 2. Treating the result as an unsigned binary integer, add 1. For example: 18 = 00010010 (two’s complement) bitwise complement = 11101101 + 1 ------------- 11101110 = - 18 As expected, the negative of the negative of that number is itself:
- 137. 136 -18 = 11101110 (two’s complement) bitwise complement = 00010001 + 1 ------------ 00010010 = 18 We can demonstrate the validity of the operation just described using the definition of the two’s complement representation in Equation (8-1). Again, interpret an n-bit sequence of binary digits an-1an-2 …. a1a0 as a two’s-complement integer A, so that its value is n-2 A = -2n-1 an-1 + Σ2i ai I=0 Now form the bitwise complement, an-1 an-2 … a0, and treating this as an unsigned integer, add 1. Finally, interpret the resulting n-bit sequence of binary digits as a two’s complement integer B, so that its value is n-2 B = -2n-1 an + 1 + Σ2i ai I=0 Now, we want A = - B, which means A + B = 0. This is easily shown to be true: n-2 A + B = - (an +n)2n-1 + 1 + Σ2i (ai + ai) I=0 n-2 = -2n-1 + 1 + Σ2i I=0 = -2n-1 + 22-1 = 0
- 138. 137 The above derivation assumes that we can first treat the bitwise complement of A as an unsigned integer to add 1, and then treat the result as a two’s complement integer. There are two special cases to consider. First, consider A = 0. In that case, for an 8-bit representation, 0 = 00000000 (two’s complement) bitwise complement = 11111111 + 1 ----------- 1 00000000 = 0 There is an overflow, which is ignored. The result is that the negation of 0 is 0, as it should be. The second special case is more of a problem. If we take the negation of the bit pattern of 1 followed by n – 1 zeros, we get back the same number. For example, for 8-bit words, -128 = 10000000 (two’s complement) bitwise complement = 01111111 + 1 ------------ 10000000 = -128 Some such anomaly is unavoidable. The number of different bit patterns in an n-bit word is 2n , which is an event number. We wish to represent positive and negative integers and 0. If an equal number of positive and negative integers are represented (sign-magnitude), then there are two representations for 0. If there is only one representation of 0 (two’s complement), then there must be an unequal number of negative and positive numbers represented. In the case of two’s complement, there is an n-bit representation for –2n , but not for 2n . Addition in two’s complement is illustrated in Figure 8.3. The first four examples illustrate successful operation. If the result of the operation is positive, we get a positive number in ordinary binary notation. If the result of the operation is negative, we get a negative number in two’s complement form. Note that, in some instances, there is a carry bit beyond the end of the word. This is ignored. On any addition, the result may be larger than can be held in the word size being used. This condition is called overflow. When overflow occurs, the ALU must signal this fact so that no attempt is made to use the result. To detect overflow, the following rule is observed.
- 139. 138 OVERFLOW RULE: If two numbers are added, and they are both positive or both negative, then overflow occurs if and only if the result has the opposite sign. (a) (-7) + (+5) (b) (-4) + (+4) 1001 1100 0101 0100 ------ ------- 1110 = -2 (1) 0000 0000 = 0 (c)(+3) + (+4) (d) (-4) + (-1) 0011 1100 0100 1111 -------- -------- 0111 = 7 (1) 1011 1011 = - 5 (e) (+5) + (+4) (f) (-7) + (-6) 0101 1001 0100 1010 ------ ------ 1001 = overflow (1) 0011 = Overflow FIGURE 8.3. Addition of numbers in two’s complement representation Fig and f show examples of overflow. Note that overflow can occur whether or not there is a carry. Subtraction is also easily handled:
- 140. 139 THE LECTURES IN A GO!!!!!! 1. Explanation of ALU. 2. Integer representation ,Sign magnitude 3. Two’s complement representation 4. Converting between different bit length 5. Fixed Point representation. 6. integer Arithmetic. Questions: 1.Explain with examples the overflow rule of the addition of numbers? 2.Explain about 2’s complement? 3.Explain the integer representation? 4.Draw the ALU diagram? References: 1. Digital Logic and Computer Design—Moris Mano ---Prentice Hall Of India 2. Computer System Architecture ---Moris Mano---“
- 141. 140 Lecture 13 Contd…. Hello students! I am going to continue with the previous topic. SUBTRACTION RULE: To subtract one number (subtrahend) from another (minuend), take the two’s complement of the subtrahend and add it to the minuend. Thus, subtraction is achieved using addition, as illustrated in Fig The last two examples demonstrate that the overflow rule still applies. Fig suggests the data paths and hardware elements needed to accomplish addition and subtraction. The cental element is a binary adder, which is presented two numbers for addition and produces a sum and an overflow indication. The binary adder treats the two numbers as unsigned integers. (A logic implementation of an adder is given in the appendix to this book). For addition, the two numbers are presented to the adder from two registers, designated in this case as A and B registers. The result is typically stored in one of these registers rather than a third. The overflow indication is stored in a 1-bit Overflow Flag (0 = no overflow; 1 = overflow). For subtraction, the subtrahend (B register) is passed through a complement so that its two’s complement is presented to the adder. Multiplication Compared with addition and subtraction, multiplication is a complex operation, whether performed in hardware or software. A wide variety of algorithms have been used in various computers. The purpose of this subsection is to give the reader some fell for the type of approach typically taken. We begin with the simpler problem of multiplying two unsigned (nonnegative) integers, and then we look at one of the most common techniques for multiplication of numbers in two’s complement representation.
- 142. 141 a)M=2=0010 b) M=-5= 1011 S =7=0111 S = 2= 0010 S’= 1001 S’ 1110 0010 1011 + 1001 + 1110 1011 = -5 1 1001 1001 = -7 FIGURE 13.1 Subtraction of numbers in two’s complement notation (M-S) Unsigned Integers Fig illustrates the multiplication of unsigned binary integers, as might be carried out using paper and pencil. Several important observations can be made: 1. Multiplication involves the generation of partial products, one for each digit in the multiplier. These partial products are then summed to produce the final product. 2. The partial products are easily defined. When the multiplier bit is 0, the partial product is 0. When the multiplier is 1, the partial product is the multiplicand. Figure 13.2 Block diagram of hardware for addition and subtraction B Register Complementer Adder A Register OF
- 143. 142 1011 Multiplicand (11) X 1101 Multiplier (13) ----- 1011 0000 1011 Partial Products 1011 ------------ 10001111 Product (143) Fig. Multiplication of unsigned binary integers 3. The total product is produced by summing the partial products. For this operation, each successive partial product is shifted one position to the left relative to the preceding partial product. 4. The multiplication of two n-bit binary integers results in a product of up to 2n bits in length. Compared with the pencil-and paper approach, there are several things we can do to make the operation more efficient. First, we can perform a running addition on the partial products rather than waiting until the end. This eliminates the need for storage of all the partial products; fewer registers are needed. Second, we can save some time on the generation of partial products. For each 1 on the multiplier, an add and a shift operation are required; but for each 0, only a shift is required. Fig 13.1 shows a possible implementation employing these measures. The multiplier and multiplicand are loaded into two registers (Q and M). A third register, the A register, is also needed and is initially set to 0. There is also a 1-bit C register, initialized to 0, which holds a potential carry bit resulting from addition. The operation of the multiplier is as follows. Control logic reads the bits of the multiplier one at a time. If Q0 is 1, then the multiplicand is added to the A Register and the result is stored in the A register. Then, all of the bits of the C, A, and Q registers are shifted to the right one bit, so that the C bit goes into An-1, Ao goes into Qn-1, and Q0 is lost. If Q0 is 0, then no addition is performed, just the shift. This process is repeated for each bit of the original multiplier. The resulting 2n-bit product is contained in the A and Q registers. A flowchart of the operation is
- 144. 143 shown in Fig, and an example is given in Fig. Note that on the second cycle, when the multiplier bit is 0, there is no add operation. Two’s complement multiplication We have seen that addition and subtraction can be performed on numbers in two’s complement notation by treating them as unsigned integers. Consider: 1001 +0011 -------- 1100 If these numbers are considered to be unsigned integers, then we are adding 9 (1001) plus 3 (0011) to get (1100). As two’s complement integers, we are adding –7 (1001) to 3 0011) to get – 4 (1100). Multiplicand (a)Block Diagram r M n-1 M o n-Bit Adder Shift and Add Control Logic Q n 1 Q o A n-1 Ao c Shift right Add
- 145. 144 C A Q 0 0000 1101 initial values 0 1011 1101 0 0101 1110 Add shift} First Cycle 0 0010 1111 Shift} Second Cycle 0 1101 1111 0 0110 1111 Add Shift} Third Cycle 1 0001 1111 Add 0 1001 1111 Shift} Fourth Cycle (Product in A, Q) (b) Example Fig.13.3 Hardware implementation of unsigned binary multiplication (M contains 1011) Unfortunately, this simple scheme will not work for multiplication. To see this, consider again Fig.13.3 We multiplied 11 (1011) by 13 (1101) to get 143 (10001111). If we interpret these as two’s complement numbers, we have-5(1011) times – 3 (1101) equals –113 (10001111). This example demonstrates that straight-forward multiplication will not work if both the multiplicand and multiplier are negative. If fact, it will not work if either the multiplicand or the multiplier is negative. To explain this statement, we need to go back to Figure 8.6 and explain what is being done in terms of operations with powers of 2. Recall that any unsigned binary number can be expressed as a sum of powers of 2. Thus, 1101 = 1 * 23 = 1 * 22 + 0 * 21 + 1 * 20 = 23 + 22 + 20 further, the multiplication of a binary number by 2n is accomplished by shifting that number to the left n bits to.
- 146. 145 Make the generation of partial products by multiplication explicit. The only difference in Figure 8.9 is that it recognizes that the partial products should be viewed as 2n-bit numbers generated from the n-bit multiplicand. Thus, as an unsigned integer, the 4-bit multiplicand 1011 is stored in an 8-bit word as 00001011. Each partial product (other than that for 20 ) consists of this number shifted to the left, with the unoccupied positions on the right filled with zeros (e.g., a shift to the left of two places yields 00101100). 1011 x 1101 ---------------- 00001011 1011 x 1 x 20 00000000 1011 x 0 x 21 00101100 1011 x 1 x 22 01011000 1011 x 1 x 23 -------------- 10001111 Fig. Multiplication of two unsigned 4-bit integers yielding an 8-bit result Now we can demonstrate that straightforward multiplication will not work if the multiplicand is negative. The problem is that each contribution of the negative multiplicand as a partial product must be a negative number on a 2n-bit field; the sign bits of the partial products must line up. This is demonstrated in Figure 8.10, which shows that multiplication of 1001 by 0011. If these are treated as unsigned integers, the multiplication of 9 * 3 = 27 proceeds simply. However, if 1001 is interpreted as the two’s complement – 7, then each partial product must be a negative two’s complement number of 2n (8) bits, as shown in Figure 8.10b. Note that this could be accomplished by padding out each partial product to the left with binary 1s. It should also be clear that if the multiplier is negative, straightforward multiplication will not work. The reason is that the bits of the multiplier no longer correspond to the shifts or multiplications that must take place. For example:
- 147. 146 -3 = 11-1 = -(0 * 23 + 0 * 22+ + 1 * 21 + 1 * 20 ) = -21 - 20 So this multiplier cannot be used directly in the manner we have been describing. There are a number of ways out of this dilemma. One would be to convert both multiplier and multiplicand to positive numbers, perform the multiplication, and then take the two’s complement of the result if and only if the sign of the two original numbers differed. Implementers have preferred to use techniques that do not require this final transformation step. One of the most common of these is Booth’s algorithm [BOOT51]. This algorithm also has the benefit of speeding up the multiplication process, relative to a more straightforward approach. Booth’s algorithm is depicted in Figure 8.11 and can be described as follows. As before, the multiplier and multiplicand are placed in the Q and M registers, respectively. There is also a 1-bit register placed logically to the right of the least significant bit (Q0) of the register and designated Q-1; its use is explained shortly. The results of the multiplication will appear in the A and Q registers. A and Q-1 are initialized to 0. As before, control logic scans the bits of the multiplier one at a time. Now, as each bit is examined, the bit to its right is also examined. If the two bits are the same (1-1 or 0-0), then all of the bits of the A, Q, and Q-1 registers are shifted to the right 1 bit. If the two bits differ, then the multiplicand is added to or subtracted from the A register, according as the two bits are 0-1 or 1-0. Following the addition or subtraction, the right shift occurs. In either case, the right shift is such that the leftmost bit of A, namely An-1, not only is shifted into An-2, but also remains in An –1. This is requi9red to preserve the sign of the number in A and Q. It is known as an arithmetic shift, since it preserves the sign bit. 1001 (9) 1001 (-7) x0011 (3) x0011 (3) ---------------- ------------------------ 00001001 (1001) x 20 11111001 (-7) x 20 + =(-7) 00010010 (1001) x 21 11110010 (-&) x 21 = (-14) 00011011 (27) 11101011 (-21) (a) Unsigned Integers (b) Two’s Complement Integers Fig. Comparison of multiplication of unsigned and two’s complement integers
- 148. 147 FIGURE 8.11. Booth’s algorithm for two’s complement multiplication Fig shows the sequence of events in Booth’s algorithm for the multiplication of 7 by 3. More compactly, the same operation is depicted in Figure The rest of Figure gives other examples of the algorithm. As can be seen, it works with any combination of positive and negative numbers. Note also the efficiency of the algorithm. Blocks of 1s or 0s are skipped over, with an average of only one addition or subtraction per block.
- 149. 148 A Q Q-1 0000 0011 0 Initial 1001 0011 0 A <- A – M} First Cycle 1100 1001 1 Shift 1110 0100 1 Shift } Second Cycle 0101 0100 1 A<- A + M} Third Cycle 0010 1010 0 Shift 0001 0101 0 Shift } Fourth Cycle (Product in A, Q) Fig. Example of Booth’s algorithm (M contains 0111) 0111 0111 x 0011 (0) x1101 (0) --------------------- -------------------- 1111101 1-0 11111001 1-0 000000 1-1 0000111 0-1 000111 0-1 111001 1-0 ----------------------- ---------------------- 00010101 (21) 11101011 (-21) (a) (7) x (3) = (21) (b) (7) x (-3) = (-21) 0111 0111 x 0011 (0) x1101 (0) --------------------- -------------------- 00000111 1-0 00000111 1-0 000000 1-1 1111001 0-1 111001 0-1 00010101 1-0 ----------------------- ---------------------- 11101011 (-21) 01001010 (21) (c)(-7) x (3) = (-21) (d) (-7) x (-3) = (-21) Fig. Examples using Booth’s alogirithm
- 150. 149 Why does Booth’s algorithm work? Consider first the case of a positive multilier. In particular, consider a positive multiplier consisting of one block of 1s surrounded by 0s, for example, 00011110. As we know, multiplication can be achieved by adding appropriately shifted copies of the multiplicand: M * (00011110) = M * (24 + 23 + 22 + 21) = M * (16 + 8 + 4 + 2) = M * 30 The number of such operations can be reduced to two if we observe that 2n + 2n-1 + … + 2n-k = 2n_1 – 2n-k Thus, M * (00011110) = M * 25 – 2n ) = M * (32 –2) = M * 30 So the product can be generated by one addition and one subtraction of the multiplicand. This scheme extends to any number of blocks of 1s in a multiplier, including the case in which a single 1 is treated as a block. Thus, M * (01111010) = M * 26 + 25 + 24 + 23 + 21 ) = M * 27 – 23 + 22 – 21 ) Booth’s algorithm conforms to this scheme by performing a subtraction when the first 1 of the block is encountered (1-0) and an addition when the end of the block is encountered (0-1). To show that the same scheme works for a negative multiplier, we need to observe the following. Let X be a negative number in two’s complement notation: Representation Of X + {1xn – 2xn-3 …. X1x0}
- 151. 150 Then the value of X can be expressed as follows: X = -22-1 + xn-2 * 2n-2 + xn-3 * 2n-3 + …. + x2 * 21 + x0 * 20 (8-3) The reader can verify this by applying the algorithm to the numbers in Table 8.1. Now, we know that the leftmost bit of X is 1, since X is negative. Assume that the leftmost 0 is the kth position. Thus, X is of the form Representation of X = {111 … 10xk-1 xk-2 ….x1x0} (-4) Then the value of X is X = -2n-1 + 2n-2 + … + 2k+1 + xk-1 * 2k-1 + … + x0 * 20 (8-5) Now, from Equation 8-2 we can say that 2b-2 + 2n3 + …. + 2k+1 = 2n-1 – 2k+1 Rearranging -2n-1 + 2n-3 + …. + 2k+1 = - 2k+1 (8-6) Substituting Equation 8-6 into Equation 8-5, we have X = -2kj+1 + xk-1 * 2k-1 + … + x0 * 20 (8-7) At last we can return to Booth’s algorithm. Remembering the representation of X (Equation 8-4), it is clear that all of the bits from X-0 up to the leftmost 0 are handled properly, since they produce all of the terms in Equation 8-7 but (-2k+1 ) and thus are in the proper form. As the algorithm scans over the leftmost 0 and encounters the next 1 (2k+1 ), 1-0 transition occurs and a subtraction takes place (-2k+1 ). This is the remaining term in Equation 8-7. As an example, consider the multiplication of some multiplicand by (-6). In two’s complement representation, using an 8-bit word, (-6) is represented as 11111010.By Equation 8-3, we know that
- 152. 151 -6 = -27 + 26 + 25 + 24 + 23 + 21 which the reader can easily verify. Thus, M2 * (11111010) = M * (-27 + 26 + 25 + 24 + 23 + 21 ) M * (11111010) = M * (-23 + 21 ) Which the reader can verify is still M * (-6). Finally, following our earlier line of reasoning, M * (11111010) = M * (-23 + 22 – 21 ) But now we can see that Booth’s algorithm conforms to this scheme. It performs a subtraction when the first 1 is encountered (1-0), an addition when (0-1) is encountered, and finally another subtraction when the first 1 of the next block of 1s is encountered. Thus, Booth’s algorithm performs fewer additions and subtractions than a more straightforward algorithm. Unsigned Binary Numbers Introduction: This unit presents the arithmetic of unsigned binary numbers. There are four sections covering the addition, subtraction, multiplication, and division of unsigned binary numbers. Section 1 - Addition of Unsigned Numbers Section 2 - Subtraction of Unsigned Numbers Section 3 - Multiplication of Unsigned Numbers Section 4 - Division of Unsigned Numbers ADDITION OF UNSIGNED NUMBERS 1. Addition with unsigned fixed-point binary numbers is done in the same way as with numbers in the decimal system. 2. Since a binary digit may take on one of two values, a simple table lookup suffices to determine the carry and sum for adding two binary digits
- 153. 152 3. In the addition operation, one adds the addend to the augend resulting in the sum and a 1- bit carry. The size of the sum is one bit more than the size of the larger of the addend or the augend. The extra bit accounts for the possibility of the carry bit. 4. Addition is commutative, hence either number to be added can be the augend and the other the addend. Addition: Augend+Addend = Carry, Sum Addend + 0 1 0 0,0 0,1 Augend 1 0,1 1,0 Example : 10012+01012=? Solution: Carry 1 10012 Augend 910 + 01012 + Addend + 510 11102 Carry,Sum 1410 10012+01012=11102 Example : 11102+01112=? Solution: Carry 11 11102 Augend 1410 + 01112 + Addend + 710 101012 Carry,Sum 2110 11102+01112=111012 Subtraction Of Unsigned Numbers 1. Subtraction with unsigned fixed-point binary numbers is done in the same way as with numbers in the decimal system. 2. Since a binary digit may take on one of two values, a simple table lookup suffices to determine the carry and sum for adding two binary digits or the borrow and difference for subtracting two binary digits.
- 154. 153 3. In the subtraction operation , one subtracts the subtrahend from the minuend resulting in the difference and a 1-bit borrow. The size of the difference is one more than the size of the larger of he minuend or the subtrahend to account for the possibility of the borrow bit. 4. While the addition operation is commutative, the subtraction operation is not commutative, hence, it is crucial not to confuse the inuend and the subtrahend. Subtraction: Minuend-Subtrahend = Borrow, Difference Subtrahend - 0 1 0 0,0 1,1 Minuend 1 0,1 0,0 Example 10012-00102=? Solution: Borrow 11 10012 Minuend 910 - 00102 - Subtrahend - 210 01112 Borrow, Difference 710 10012-00102=01112 Example 00112-01102=? Solution: Borrow 1 00112 Minuend 310 - 01102 - Subtrahend - 610 111012 Borrow, Difference -310 (-16+13) 00112-01102=111012 (The carry represents a borrow of 16. The rest of the bits 1101 epresent a positive Floating point unit A floating point unit (FPU) is a part of a CPU specially designed to carry out operations on floating point numbers. Typical operations are floating point arithmetic (such as addition and
- 155. 154 multiplication), but some systems may be capable of performing exponential or trigonometric calculations as well (such as square roots or cosines). Not all CPUs have a dedicated FPU. In the absence of an FPU, the CPU may use a microcode program to emulate an FPUs function using an arithmetic and logical unit (ALU), which saves the added hardware cost of an FPU but is significantly slower. In some computer architectures, floating point operations are handled completely separate from integer operations, with dedicated floating point registers and independent clocking schemes. Floating point addition and multiplication operations are typically pipelined, but more complicated operations, like division, may not be, and some systems may even have a dedicated floating point divider circuit. Floating Point 0 1 8 9 31 fig. 32 BIT FLOATING POINT •+/- .significand x 2exponent •Misnomer •Point is actually fixed between sign bit and body of mantissa •Exponent indicates place value (point position) fig. Expressible numbers in typical 32-bit formats Sign bit Biased exponent Significant or mantessa
- 156. 155 Fig Density of floating –point numbers IEE Standard for Binary Floating-Point Arithmetic THE LECTURES IN A GO!!!!!!!! Arithmetic & Logic Unit •Does the calculations •Everything else in the computer is there to service this unit •Handles integers •May handle floating point (real) numbers •May be separate FPU (maths co-processor) •May be on chip separate FPU (486DX +) Integer ALU Inputs and Outputs
- 157. 156 Representation • Only have 0 & 1 to represent everything • Positive numbers stored in binary e.g. 41=00101001 • No minus sign • No period • Sign-Magnitude • Two’s compliment Sign-Magnitude • Left most bit is sign bit • 0 means positive • 1 means negative • +18 = 00010010 • -18 = 10010010 • Problems Need to consider both sign and magnitude in arithmetic Two representations of zero (+0 and -0) Two’s Compliment • +3 = 00000011 • +2 = 00000010 • +1 = 00000001 • +0 = 00000000 • -1 = 11111111 • -2 = 11111110 • -3 = 11111101 Benefits • One representation of zero • Arithmetic works easily (see later) • Negating is fairly easy 3 = 00000011 Boolean complement gives 11111100 Add 1 to LSB 11111101 Negation Special Case 1 • 0 = 00000000 • Bitwise not 11111111
- 158. 157 • Add 1 to LSB +1 • Result 1 00000000 • Overflow is ignored, so: • - 0 = 0 √ Negation Special Case 2 • -128 = 10000000 • bitwise not 01111111 • Add 1 to LSB +1 • Result 10000000 • So: • -(-128) = -128 X • Monitor MSB (sign bit) • It should change during negation Range of Numbers • 8 bit 2s compliment +127 = 01111111 = 27 -1 -128 = 10000000 = -2716 bit 2s compliment +32767 = 011111111 11111111 = 215 - 1 -32768 = 100000000 00000000 = -215
- 159. 158 Hardware for Addition and Subtraction Unsigned Binary Multiplication Multiplying Negative Numbers • This does not work! • Solution 1 Convert to positive if required Multiply as above If signs were different, negate answer • Solution 2 Booth’s algorithm Emerging trends Emerging new CPU architectures include: • Intel's Itanium architecture • AMD's x86-64 architecture Historically important CPUs have been: • EDSAC- the first stored-program computer Apollo Guidance Computer, used in the moon flights
- 160. 159 Question 1. What is a CPU? Explain in details? 2. What is a ALU ?Explain in details? 3. Explain the addition , subtraction , division method? 4. Draw the diagram of Booths Algorithm with example? 5. Write short note on Floating Point with Eg ? 6. Find the following differences using two’s complements : a. 111000 b. 11001100 c. 111100001111 d. 11000011 b. – 110011 - 101110 - 110011110011 - 11101000 7. Is the following a valid alternative definition of overflow in two’s complement arithmetic? 8. Perform the following arithmetic operations with the decimal numbers using signed 10’s complement representation for the following negative numbers. a. (-638) + (+785) b. (-638) + (+185) 9. Perform the subtraction with the following unsigned binary numbers taking the 2’s complement of the subtrahend. a. 11010 – 10000 b. 11010 – 1101 c. 100 – 110000 d. 1010100 – 1010100 10. Obtain the 10’s complement of the following six-digit decimal numbers 12349876 ; 090657; 100000 ; 000000 References: 1.Computer Systems Architecture --- M.Morris Mano ---Prentice Hall Of India 2.Digital Logic and Computer Design --- M.Morris Mano ---Prentice Hall Of India
- 161. 160 Lecture 14 COMBINATIONAL LOGIC Objectives of the lecture: 1.To understand the basics circuits and the combinational logics. Introduction Hello friends! Today let us discuss on the important topic of basics circuits. Logic circuits for digital systems may be Combinational or Sequential. A Boolean functions may be practically implemented by using logic gates. The following points are important to understand. • Electronic gates require a power supply. • Gate INPUTS are driven by voltages having two nominal values, e.g. 0V and 5V representing logic 0 and logic 1 respectively. • The OUTPUT of a gate provides two nominal values of voltage only, e.g. 0V and 5V representing logic 0 and logic 1 respectively. • There is always a time delay between an input being applied and the output responding. Logic gates Digital systems are said to be constructed by using three basic logic gates. These gates are the AND gate, OR gate and NOT gate. There also exists other logical gates, like the NAND, and the EOR gates. We will only be looking at the first three gates. The basic operations are described below. AND gate The AND gate is an electronic circuit that gives a high output (1) only if all its inputs are high. A dot (.) is used to show the AND operation. Bear in mind that this dot is usually omitted, as shown at the output above.
- 162. 161 OR gate The OR gate is an electronic circuit that gives a high output if one or more of its inputs are high. A plus (+) is used to show the OR operation. NOT gate The NOT gate is an electronic circuit that produces an inverted version of the input's logic at its output. It is also known as an inverter. If the input variable is A, the inverted output is known as NOT A. This is also shown as A', or A with a bar over the top, as shown at the outputs above. NAND gate This is a NOT-AND circuit which is equal to an AND circuit followed by a NOT circuit. The outputs of all NAND gates are high if any of the inputs are low. NOR gate This is a NOT-OR circuit which is equal to an OR circuit followed by a NOT circuit. The outputs of all NOR gates are low if any of the inputs are high. EXOR gate The 'Exclusive-OR' gate is a circuit which will give a high output if either, but not both, of its two inputs are high. An encircled plus sign ( ) is used to show the EOR operation. The NAND and NOR are called universal functions since with either one the AND and OR functions and NOT can be generated. Note: A function in sum of products form can be implemented using NAND gates by replacing all AND and OR gates by NAND gates. A function in product of sums form can be implemented using NOR gates by replacing all AND and OR gates by NOR gates.
- 163. 162 Table 1: Logic gate symbols Table 2 shows the input/output combinations for the NOT gate together with all possible input/output combinations for the other gate functions. Also note that a truth table with 'n' inputs has 2n rows. Table 2: Logic gates representation using the Truth table Example A NAND gate can be used as a NOT gate using the following wiring. (You can check this out using a truth table.)
- 164. 163 Problem Draw the circuit diagrams like the ones in the example above to show how a NOR gate can be made into a NOT gate. A combinational circuit consists of logic gates whose outputs at any time are determined directly from the present combination of inputs without regard to previous inputs. A combinational circuit performs a specific information-processing operation fully specified logically by a set of Boolean functions. Sequential circuits employ memory elements (binary cells) in addition to logic gates. Their outputs are a function of the inputs and the state of the memory elements. The state of memory elements, in turn, is a function of previous inputs. As a consequence, the outputs of a sequential circuit depend not only on present inputs, but also on past inputs, and the circuit behavior must be specified by a time sequence of inputs and internal states, Sequential circuits are discussed in We learned to recognize binary numbers and binary codes that represent discrete quantities of information. These binary variables are represented by electric voltages or by some other signal. The signals can be manipulated in digital logic gates to perform required functions. In the previous chapter I have introduced Boolean algebra as a way to express logic functions algebraically and we learned how to simplify Boolean functions to achieve economical gate implementations. The purpose of this chapter is to use the knowledge acquired in previous chapter and formulate various systematic design and analysis procedures of combinational circuits. The solution of some typical examples will provide a useful catalog of elementary functions important for the understanding of digital computers and systems. A combinational circuit consists of input variables, logic gates, and output variables. The logic gates accept signals from the inputs and generate signals to the outputs. This process transforms binary information from the given input data to the required output data. Obviously, both input and output data are represented by binary signals, i.e., they exist in two possible values, one representing logic-1 and the other Figure 14.1 Block Diagram of Combinational Cicuit logic-0. A block diagram of a combinational circuit is shown in Fig.14.1 Combinational Logic Circuit m Output Variables nInput Variables
- 165. 164 The n input binary variables come from an external source; the m output variables go to an external destination. In many applications, the source and/or destination are the storage registers located either in the vicinity of the combinational circuit or in a remote external device. By defination, an external register does not influence the behavior of the combinational circuit because, if it does, the total system becomes a sequential circuit. For n input variables, there are 2n possible combinations of binary input values. For each possible input combination, there is one and only one possible output combination. A combinational circuit can be described by m Boolean functions, one for each output variable. Each output function is expressed in terms of the n input variables. Each input variable to a combinational circuit may have one or two wires. When only one wire is available, it may represent the variable either in the normal form (unprimed) or in the complement form (primed). Since a variable in a Boolean expression may appear primed and/or unprimed, it is necessary to provide an inverter for each literal not available in the input wire. On the other hand, an input variable may appear in two wires, supplying both the normal and complement forms to the input of the circuit. If so, it is unnecessary to include inverters for the inputs. The type of binary cells used in most digital systems are flip/flop circuits that have output for both the normal and complement values of the stored binary variable. In our subsequent work, we shall assume that each input variable appears in two wires, supplying both the normal and complement values simultaneously. We must also realize that an inverter circuit can always supply the complement of the variable if only one wire is available. DESIGN PROCEDURE The design of combinational circuits starts from the verbal outline of the problem and ends in a logic circuit diagram, or a set of Boolean functions from which the logic diagram can be easily obtained. The procedure involves the following steps: 1. The problem is stated. 2. The number of available input variables and required output variables is determined. 3. The input and output variables are assigned letter symbols. 4. The truth table that defines the required relationships between inputs and outputs is derived. 5. The simplified Boolean function for each output is obtained. 6. The logic diagram is drawn.
- 166. 165 A truth table for a combinational circuit consists of consists of input columns and output columns. The l’s and O’s in the input columns are obtained from the 2n binary combinations available for n input variables. The binary values for the outputs are determined from examination of the stated problem. An output can be equal to either 0 to 1 for every valid input combination. However, the specifications may indicate that some input combinations will not occur. These combinations become don’t-care conditions. The output functions specified in the truth table give the exact definition of the combinational circuit. It is important that the verbal specifications be interpreted correctly into a truth table. Sometimes the designer must use his intuition and experience to arrive at the correct interpretation. Word specifications are very seldom complete and exact. Any wrong interpretation which results in an incorrect truth , table produces a combinational circuit that will not fulfill the stated requirements. The output Boolean functions from the truth table are simplified by any available method, such as algebraic manipulation, the map method, or the tabulation procedure. Usually there will be a variety of simplified expressions from which to choose. However, in any particular application, certain restrictions, limitations, and criteria will serve as a guide in the process of choosing a particular algebraic expression. A practical design method would have to consider such constraints as (1) minimum number of gates, (2) minimum number of inputs to a gate, (3) minimum propagation time of the signal through the circuit, (4) minimum number of interconnections and (5) limitations of the driving capabilities of each gate. Since all these criteria cannot be satisfied simultaneously, and since the importance of each constraint is dictated by the particular application, it is difficult to make a general statement as to what constitutes an acceptable simplification. In most cases the simplification begins by satisfying an elementary objective, such as producing a simplified Boolean function in a standard form, and from that proceeds to meet any other performance criteria. In practice, designers tend to go from the Boolean functions to a wiring list that shows the interconnections among various standard logic gates. In that case the design need not go any further than the required simplified output Boolean functions. However, a logic diagram is helpful for visualizing the gate implementation of the expressions. ADDERS Digital computers perform a variety of information-processing tasks. Among the basic functions encountered are the various arithmetic operations. The most basic arithmetic operation, no doubt, is the addition of two binary digits. This simple addition consists of four possible elementary operations, namely, 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, and 1 + 1 = 10. The first three operations produce a sum whose length is one digit, but when both augends and addend bits are equal to l, the binary sum consists of two digits. The higher significant bit of this result is called
- 167. 166 a carry. When the augend and addend numbers contain more significant digits, the carry obtained from the addition of two bits is added to the next higher-order pair of significant bits. A combinational circuit that performs the addition of two bits is called a half-adder. One that performs the addition of three bits (two significant bits and a previous carry) is a full-adder. The name of the former stems from the fact that two half-adders can be employed to implement a full-adder. The two adder circuits are the first combinational circuits we shall design. Half-Adder From the verbal explanation of a half-adder, we find that this circuit needs two binary inputs and two binary outputs. The input variables designate the augend and addend bits; the output variables produce the sum and carry. It is necessary to specify two output variables because the result may consist of two binary digits. We arbitrarily assign symbols x and y to the two inputs and S (for sum) and C (for carry) to the outputs. Now that we have established the number and names of the input and output variables, we are ready to formulate a truth table to identify exactly the function of the half-adder. This truth table is shown below: x y C S 0 0 0 0 0 1 0 1 1 0 0 1 1 1 1 0 The carry output is 0 unless both inputs are 1. The S output represents the least significant bit of the sum. The simplified Boolean functions for the two outputs can be obtained directly from the truth table. The simplified sum of products expressions are : S = x’y + xy’ C = xy
- 168. 167 x s y C a) Logic Diagram x y C S 0 0 0 1 1 0 1 1 0 0 0 1 0 1 1 0 (b) Truth table Figure 14.2 Implementation of a half-adder The logic diagram for this implementation is shown in Fig. 14-2(a), four other implementations for a half-adder. They all achieve the same result as far as the input-output behavior is concerned. They illustrate the flexibility available to the designer when implementing even a simple combinational logic function such as this. Figure 14-2(a), as mentioned above, is the implementation of the half-adder in sum of products. Figure 14-2(b) shows the implementation in product of sums: S = (x + y) (x’ y’) C = xy
- 169. 168 To obtain the implementation of Fig. 4-2(c), we note that S is the exclusive-OR of x and y. The complement of S is the equivalence of x and y (Section 2-6): S’ = xy + x’y’ but C = xy, and therefore we have: S = (C + x’y’)’ In Fig. we use the product of sums implementation with C derived as follows : C = xy = (x’ + y’) The half-adder can be implemented with an exclusive-OR and an AND gate as shown in Fig. 4- 2(e). This form is used later to show that two half-adder circuits are needed to construct a full- adder circuit. Full-Adder A full-adder is a combinational circuit that forms the arithmetic sum of three input bits. It consists of three inputs and two outputs. Two of the input variables, denoted by x and y, represent the two significant bits to be added. The third input z, represents the carry from the previous lower significant position. Two outputs are necessary because the arithmetic sum of three binary digits ranges in value from 0 to 3, and binary 2 or 3 needs two digits. The two outputs are designed by the symbols S for sum and C for carry. The binary variable S gives the value of the least significant bit of the sum. The binary variable C gives the output carry. The truth table of the full-adder is as follows:
- 170. 169 1 1 1 1 The eight rows under the input variables designate all possible combinations of l’s and O’s that these variables may have. The l’s and O’s for the output variables are determined from the arithmetic sum of the input bits. When all input bits are O’s, the output is O. The S output is equal to 1 when only one input is equal to 1 or when all three inputs are equal to 1. The C output has a carry of 1 if two or three inputs are equal to 1. The input and output bits of the combinational circuit have different interpretations at various stages of the problem. Physically, the binary signals of the input wires are considered binary digits added arithmetically to form a two-digit sum at the output wires. On the other hand, the same binary values are considered variables of Boolean functions when expressed in the truth table or when the circuit is implemented with logic gates. It is important to realize that two different interpretations are given to the values of the bits encountered in this circuit. The input-output logical relationship of the full-adder circuit may be expressed in two Boolean functions, one for each output variable. Each output Boolean function requires a unique map for its simplification. Each map must have eight squares, since each output is a function of three input variables. The maps of Fig. 4-3 are used for simplifying the two output functions. The l’s in the squares for the maps of S and C are determined directly from the truth table. The squares with l’s for the S output do not combine in adjacent squares to give a simplified expression in sum of products. The C output can be simplified to a six-literal expression. The x y z c S 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 0 0 0 1 0 1 1 1 0 1 1 0 1 0 0 1 1 1 1 1
- 171. 170 logic diagram for the full-adder implemented in sum of products is shown in Fig. 4-4. This implementation uses the following Boolean expressions: S = x’y’z + x’yz’ + xy’z’ + xyz C = xy + xz + yz Other configurations for a full-adder may be developed. The product-of-sums implementation requires the same number of gates as in Fig. 4-4, with the number x S y z C Figure 14-3 Implementation of full- adder with two half- adders and OR gate of AND and OR gates interchanged. A full-adder can be implemented with two half-adders and one OR gate, as shown in Fig. 4-5. The S output from the second half adder is the exclusive-OR of z and the output of the first half-adder, giving: S = z ⊕ (x ⊕ y) = z’ (xy’ _ x’y) + z (xy’ + x’y)’ = z’ (xy’ + x’y) + z (xy + x’y’) = xy’z’ + x’yz’ + xyz + x’y’z and the carry output is: C = z(xy’ + x’y) + xy = xy’z + x’yz + xy
- 172. 171 THE LECTURE ON A GO!!!!!!! 1.Introduction to the logic gates. 2.Defination with the block diagream of combinational logic 3.Adders,half adder,full adder Question: 1. Explain in short AND gates,OR ,NOR,NAND,EXOR gates? 2. What are adders? 3. Explain half adder ? 4. Explain full adder? 5. A majority function is generated in a combinational circuit when the output is equal to 1 if the input variables have more 1’s than 0’s. the output is 0 otherwise. Design a three- input majority function. 6. Design a combinational circuit with three inputs x , y , z and three outputs A , B , C. When the binary input is 0 ,1 ,2 or 3, the binary output is one greater than the input. When the binary input is 4, 5, 6, or 7, the binary output is one less than the input.
- 173. 172 Lecture 15 Hello friends!, as you all have learnt about the adders in the early lectures , let us now study about the subtractors SUBTRACTORS The subtraction of two binary numbers may be accomplished by taking the complement of the subtrahend and adding it to the minuend (Section 1-5). By this method, the subtraction operation becomes an addition operation requiring full-adders for its machine implementation. It is possible to implement subtraction with logic circuits in a direct manner, as done with paper and pencil. By this method, each subtrahend bit of the number is subtracted from its corresponding significant minuend bit to form a difference bit. If the minuend bit is smaller than the subtrahend bit, a l is borrowed from the next significant position. The fact that a l has been borrowed must be conveyed to the next higher pair of bits by means of a binary signal coming out (output) of a given stage and going into (input) the next higher stage. Just as there are half-and full-adders, there are half-and full-subtractors. Half-Subtractor A half-subtractor is a combinational circuit that subtracts two bits and produces their difference. It also has an output to specify if a I has been borrowed. Designate the minuend bit by x and the subtrahend bit by y. To perform x – y, we have to check the relative magnitudes of x and y. If x > y, we have three possibilities: 0 – 0 = 0, 1 – 0 = 1, and 1 – 1 = 0. The result is called the difference bit. If x < y, we have 0 – 1, and it is necessary to borrow a l from the next higher stage. The I borrowed from the next higher stage. The I borrowed from the next higher stage adds 2 to the minuend bit, just as in the decimal system a borrow adds 10 to a minuend digit. With the minuend equal to2, the difference becomes 2 – 1 = 1. The half-subtractor needs two outputs. One output generates the difference and will be designated by the symbol D. The second output, designated B for borrower, generates the binary signal that informs the next stage that a I has been borrowed. The truth table for the input-output relationship of a half-subtractor can now be derived as follows:
- 174. 173 x y B D 0 0 0 0 0 1 1 1 1 0 0 1 1 1 0 0 The output borrower B is a O as long as x > y. It is a l for x = 0 and y – 1. The D output is the result of the arithmetic operation 2B + x – y. The Boolean functions for the two outputs of the half-subtractor are derived directly from the truth table: D = x’y + xy’ B = x’y It is interesting to note that the logic for D is exactly the same as the logic for output S in the half-adder. Full-Subtractor A full-subtractor is a combinational circuit that performs a subtraction between two bits, taking into account that a I may have been borrowed by a lower significant stage. This circuit has three inputs and two outputs. The three inputs, x, y, and z, denote the minuend, subtrahend, and previous borrow, respectively. The two outputs, D and B, represent the difference and output borrow, respectively. The truth table for the circuit is as follows :
- 175. 174 x y z B D 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 0 1 1 1 0 0 0 1 0 1 1 0 1 0 0 1 Figure 4-6 Maps of full- subtractor The eight rows under the input variables designate all possible combinations of l’s and O’s that the binary variables may take. The l’s and O’s for the output variables are determined from the subtraction of x – y – z. The combinations having inputs borrow z = 0 reduce to the same four conditions of the half-adder. For x = 0, y = 0, and z = 1, we have to borrow a l from the next stage, which makes B = 1 and adds 2 to x. Since 2 – 0 – 1, D = 1. For x = 0 and yz = 11, we need to borrow again, making B = 1 and x = 2. Since 2 – 1 – 1 = 0, D = 0. For x = 1 and yz = 01, we have x – y – z = 0, which makes B = 0 and D = 0. Finally, for x = 1, y = 1, z = 1, we have to borrow, I making B = 1 and x = 3, and 3 – 1 – 1 = 1, making D = 1. The simplified Boolean functions for the two outputs of the full-subtractor are derived in the maps of Fig. 4-6. The simplified sum of products output functions are : D = x’y’z + x’yz’ + xy’z’ + xyz B = x’y + x’z + yz Again we note that the logic function for output D in the full-subtractor is exactly the same as output S in the full-adder. Moreover, the output B resembles the function for C in the full-adder, except that the input variable x is complemented. Because of these similarities, it is possible to convert a full-adder into a full-subtractor by merely complementing input x prior to its application to the gates that form the carry output.
- 176. 175 CODE CONVERSION The availability of a large variety of codes for the same discrete elements of information results in the use of different codes by different digital systems. It is sometimes necessary to use the output of one system as the input to another. A conversion circuit must be inserted between the two systems if each uses different codes for the same information. Thus, a code converter is a circuit that makes the two systems compatible even though each uses a different binary code. To convert from binary code A to binary code B, the input lines must supply the bit combination of elements as specified by code A and the output lines must generated the corresponding bit combination of code B. A combinational circuit performs this transformation by means of logic gates. The design procedure of code converters will be illustrated by means of a specific example of conversion from the BCD to the excess-3 code. The bit combinations for the BCD and excess-3 codes are listed in Table 1-2 (Section 1- 6). Since each code uses four bits to represent a decimal digit, there must be four input variables and four output variables. Let us designate the four input binary variables by the symbols A, B, C, and D, and the four output variables by w, x, y, and z. The truth relating the input and output variables is shown in Table 4-1. The bit combinations for the inputs and their corresponding outputs are obtained directly from Table 1-2. We note that four binary variables may have 16 bit combinations, only 10 of which are listed in the truth table. The six bit combinations not listed for the input variables are don’t-care combinations. Since they will never occur, we are at liberty to assign to the output variables either a 1 to a 0, whichever gives a simpler circuit.
- 177. 176 Table 4.1 Truth table for code-conversion example Input BCD Output Excess 3 Code A B C D w x y z 0 0 0 0 0 0 1 1 0 0 0 1 0 1 0 0 0 0 1 0 0 1 0 1 0 0 1 1 0 1 1 0 0 1 0 0 0 1 1 1 0 1 0 1 1 0 0 0 0 1 1 0 1 0 0 1 0 1 1 1 1 0 1 0 1 0 0 0 1 0 1 1 1 0 0 1 1 1 0 0 The maps are drawn to obtain a simplified Boolean function for each output. Each of the four maps represents one of the four outputs of this circuit as a function of the four input variables. The l’s marked inside the squares are obtained from the minterm that make the output equal to 1. The l’s are obtained from the truth table by going over the output columns one at a time. For example, the columns under output z has five l’s; therefore, the map for z must have five l’s, each being in a square corresponding to the minterm that makes z equal to l. The six don’t-care combinations are marked by X’s. One possible way to simplify the functions in sum of products is listed under the map of each variable. A two-level logic diagram may be obtained directly from the Boolean expressions derived by the maps. There are various other possibilities for a logic diagram that implements this circuit. The expression obtained may be manipulated algebraically for the purpose of using common gates for two or more outputs. This manipulation, shown below, illustrates the flexibility obtained with multiple-output systems when implemented with three or more levels of gates.
- 178. 177 z = D’ y = CD + C’D’ = CD + (C + D)’ x = B’C + B’D + BC’D’ = B’ (C +D) + BC’D’ = B’ (C + D) + B (C +D)’ w = A = BC + BD = A + B (C + D) The logic diagram that implements the above expressions is shown in Fig. 4-8. In it we see that the OR gate whose output is C + D has been used to implement partially each of three outputs. Not counting input inverters, the implementation in sum of products requires seven AND gates and three OR gates. The implementation of Fig. 4-8 requires four AND gates, four OR gates, and one inverter. If only the normal inputs are available, the first implementation will require inverters for variables B, C, and D, whereas the second implementation requires for variables B and D. ANALYSIS PROCEDURE The design of a combinational circuit starts from the verbal specifications of a required function and culminates with a set of output Boolean functions or a logic diagram. The analysis of a combinational circuit is somewhat the reverse process. It starts with a given logic diagram and culminates with a set of Boolean functions, a truth table, or a verbal explanation of the circuit operation. If the logic diagram to be analyzed is accompanied by a function name or an explanation of what it is assumed to accomplish, then the analysis problem reduces to a verification of the stated function. The first step in the analysis is to make sure that the given circuit is combinational and not sequential. The diagram of a combinational circuit has logic gates with no feedback paths or memory elements. A feedback path is a connection from the output of one gate to the input of a second gate that forms part of the input to the first gate. Feedback paths or memory elements in a digital circuit define a sequential circuit and must be analyzed according to procedures outlines in Chapter 6. Once the logic diagram is verified as a combinational circuit, one can proceed to obtain the output Boolean functions and/or the truth table. If the circuit is accompanied by a verbal explanation of its function, then the Boolean functions or the truth table is sufficient for verification. If the function of the circuit is under investigation, then it is necessary to interpret the operation of the circuit from the derived truth table. The success of such investigation is
- 179. 178 enhanced if one has previous experience and familiarity with a wide verity digital circuits. The ability to correlate a truth table with an information-processing task is an art one acquires with experience. To obtain the output Boolean functions from a logic diagram, proceed as follows : 1. Label with arbitrary symbols all gate output that are a function of the input variables. Obtain the Boolean functions for each gate. 2. Label with other arbitrary symbols those gates which are a function of input variables and/or previously labeled gates. Find the Boolean functions for these gates. 3. Repeat the process outlined in step 2 until the outputs of the circuit are obtained. 4. By repeated substitution of previously defined functions, obtain the output Boolean functions in terms in input variables only. Analysis of the combinational circuit in Fig. 4-9 illustrates the proposed procedure. We note that the circuit has three binary inputs, A, B, and C, and two binary outputs, F1 and F2. The outputs of various gates are labeled with intermediate symbols. The outputs of gates that are a function in input variables only are F2 T1, and T2. The Boolean functions for these three outputs are : F2 = AB + AC + BC T1 = A + B + C T2 = ABC Next we consider outputs of gates which are a function of already defined symbols: F3 = F’2T1 F1 = T3 + T2
- 180. 179 The output Boolean function F2 expressed above is already given as a function of the inputs only. To obtain F1 as a function of A, B, and C, form a series of substitutions as follows : F1 = T3 + T2 = F’2T1 + ABC = (AB + AC + BC)’(A + B + C) + ABC = (A’ + B’) (A’ + C’) (B’ + C’) (A + B + C) + ABC = (A’ + B’C’) (AB’ + AC’ + BC’ + B’C) + ABC = A’BC’ + A’B’C + AB’C’ + ABC If we want to pursue the investigation and determine the information-transformation task achieved by this circuit, we can derive the truth table directly from the Boolean functions and try to recognize a familiar operation. For this example, we note that the circuit is a full-adder, with F1, being the sum output and F2 the carry output. A, B, and C are the three inputs added arithmetically. The derivation of the truth table for the circuit is a straightforward process once the output Boolean functions are known. To obtain the truth take directly from the logic diagram without going through the derivations of the Boolean functions, proceed as follows: 1. Determine the number of input variables to the circuit. For n inputs, form the 2n possible input combinations of l’s and O’s by listing the binary numbers from 0 to 2n – 1. 2. Label the outputs of selected gates with arbitrary symbols. 3. Obtain the truth table for the outputs of those gates that are a function of the input variables only. 4. Proceed to obtain the truth table for the output of those gates that are a function of previously defined values until the columns for all outputs are determined. This process can be illustrated using the circuit of Fig. 4-9. In Table 4-2, we form the eight possible combinations for the three input variables. The truth table for F2 is determined directly from the values of A, B, and C, with F2 equal to 1 for any combination that has two or three inputs equal to 1. The truth table for F’2 is the complement of F2. The truth tables for T1
- 181. 180 and T2 are the OR and AND functions of the input variables, respectively. The values for T3 are derived from T1 and F’2. T3 is equal to 1 when both T1 and F’2 are equal to 0 otherwise. Finally, F1 is equal to 1 for those combinations in which either T2 or T3 or both are equal to 1. Inspection of the truth table combinations for A, B, C, F1, and F2 of Table 4-2 shows that it is identical to the truth table of the full-adder given in Section 4-3 for x, y, z, S, and C, respectively. Table 4.2 Truth Table for logic diagram gig. 4.9 A B C F2 F2 T1 T2 T3 F1 0 0 0 0 1 0 0 0 0 0 0 1 0 1 1 0 1 1 0 1 0 0 1 1 0 1 1 0 1 1 1 0 1 0 0 0 1 0 0 0 1 1 0 1 1 1 0 1 1 0 1 0 0 0 1 1 0 1 0 1 0 0 0 1 1 1 1 0 1 1 0 1 Consider now a combinational circuit that has don’t-care input combinations. When such a circuit is designed, the don’t-care combinations are marked by X’s in the map and assigned an output of either 1 or 0, whichever is more convenient for the simplification of the output Boolean function. When a circuit with don’t-care combinations is being analyzed, the situation is entirely different. Even though we assume that the don’t-care input combinations will never occur, the fact of the matter is that if any one of these combinations is applied to the inputs (intentionally or in error), a binary output will be present. The value of the output will depend on the choice for the X’s taken during the design. Part of the analysis of such a circuit may involve the determination of the output values for the don’t-care input combinations. As an example, consider the BCD-to-excess-3 code converter designed in Section 4-5. The output obtained when the six unused combinations of the BCD code are applied to the inputs are:
- 182. 181 Unused BCD Input Outputs A B C D w x y z 1 0 1 0 1 1 0 1 1 0 1 1 1 1 1 0 1 1 0 0 1 1 1 1 1 1 0 1 1 0 0 0 1 1 1 0 1 0 0 1 1 1 1 1 1 0 1 0 These outputs may be derived by means of the truth table analysis method as outlined in this section. In this particular case, the outputs may be obtained directly from the maps of Fig. 4-7. From inspection of the maps, we determine whether the X’s in the corresponding minterm squares for each output have been included with the l’s or the O’s. For example, the square for minterm m10 (1010) has been included with the l’s for outputs w, x, and z, but not for y. Therefore, the outputs for m10 are wxtz = 1101, as listed in the above table. We also note that the first three outputs in the table have no meaning in the excess-3 code, and the last three outputs correspond to decimal 5, 6, and 7, respectively. This coincidence is entirely a function of the choice for the X’s taken during the design. MULTILEVEL NAND CIRCUITS Combinational circuits are more frequently constructed with NAND or NOR gates rather than AND and OR gates. NAND and NOR gates are more common from the hardware point of view because they are readily available in integrated-circuit form. Because of the prominence of NAND and NOR gates in the design of combinational circuits, it is important to be able to recognize the relationships that exist between circuits constructed with AND-OR gates and their equivalent NAND or NOR diagrams. The implementation of two-level NAND and NOR logic diagrams was presented in Section 3-6. Here we consider the more general case of multilevel circuits. The procedure for obtaining NAND circuits is presented in this section, and for NOR circuits in the next section.
- 183. 182 Universal Gate The NAND gate is said to be a universal gate because any digital system can be implemented with it. Combinational circuits and sequential circuits as well can be constructed with this gate because the flip-flop circuit (the memory element-most frequently used in sequential circuits) can be constructed from two NAND gates connected back to back, as shown in Section 6-2. To show that any Boolean function can be implemented with NAND gates, we need only show that the logical operations AND, OR and NOT can be implemented with NAND gates. The implementation of the AND, OR, and NOT operations with NAND gates is shown in, actually another symbol for an inverter circuit. The AND operation requires two NAND gates. The first produces the inverted AND and the second acts as an inverter to produce the normal output. The OR operation is achieved through a NAND gate with additional inverters in each input. A convenient way to implement a combinational circuit with NAND gates is to obtain the simplified Boolean functions in terms of AND, OR and NOT and convert the functions to NAND logic. The conversion of the algebraic expression from AND, OR and NOT operations to NAND operations is usually quite complicated because it involves a large number of applications of De Morgan’s theorem. The difficulty is avoided by the use of simple circuit manipulations and simple rules as outlines below. Boolean Function Implementation – Block Diagram Method The implementation of Boolean functions with NAND gates may be obtained by means of a simple block diagram manipulation technique. This method requires that two other logic diagrams be drawn prior to obtaining the NAND logic diagram. Nevertheless, the procedure is very simple and straightforward: 1. From the given algebraic expression, draw the logic diagram with AND, OR, and NOT gates. Assume that both the normal and complement inputs are available. 2. Draw a second logic diagram with the equivalent NAND logic, as given in Fig. 4-10, substituted for each AND, OR and NOT gate.
- 184. 183 3. Remove any two cascaded inverters from the diagram, since double inversion does not perform a logic function. Remove inverters connected to single external inputs and complement the corresponding input variable. The new logic diagram obtained is the required NAND gate implementation. This procedure is illustrated in Fig. 4-11 for the function : F = A (B + CD) + BC’ The AND-OR implementation of this function is shown in the logic diagram of Fig. 4-11(a). For each AND gate, we substitute a NAND gate followed by an inverter; for each OR gate, we substitute input inverters followed by a NAND gate. This substitution follows directly from the logic equivalences of Fig. 4-10 and is shown in the diagram of Fig. 4-11(b). This diagram has seven inverters and five two-input NAND gates listed with numbers inside the gate symbol. Pairs of inverters connected in cascade (from each AND box to each OR box) are removed since they form double inversion. The inverter connected to input B is removed and the input variable is designed by B’. The result is the NAND logic diagram shown in Fig. 4-11(c), with the number inside each symbol identifying the gate from Fig. 4-11(b). This example demonstrates that the number of NAND gates required to implement the Boolean function is equal to the number of AND-OR gates, provided both the normal and the complement inputs are available. If only the normal inputs are available, inverters must be used to generate any required complemented inputs. A second example of NAND implementation is shown in Fig. 4-12. The Boolean function to be implemented is : F = ( A + B’) (CD + E) The AND-OR implementation is shown in Fig. 4-12(a), and its NAND logic substitution, in Fig. 4-12(b). One pair of cascaded inverters may be removed. The three external inputs E, A, and B’, which go directly to inverters, are complemented and the corresponding inverters removed. The final NAND gate implementation is in Fig. 4-12(c).
- 185. 184 The number of NAND gates for the second example is equal to the number of AND-OR gates plus an additional inverter in the output (NAND gate 5). In general, the number of NAND gates required to implement a function equals the number of AND-OR gates, except for an occasional inverter. This is true provided both normal and complement inputs are available, because the conversion forces certain input variables to be complemented. The block diagram method is somewhat tiresome to use because it requires the drawing of two logic diagrams to obtain the answer in a third. With some experience, it is possible to reduce the amount of labor by anticipating the pairs of cascaded inverters and the inverters in the inputs. Starting from the procedure just outlined, it is not too difficult to derive general rules for implementing Boolean functions with NAND gates directly from an algebraic expression. Analysis Procedure The foregoing procedure considered the problem of deriving a NAND logic diagram from a given Boolean function. The reverse process is the analysis problem which starts with a given NAND logic diagram and culminate with a Boolean expression or a truth table. The analysis of NAND logic diagrams follows the same procedures presented in Section 4-6 for the analysis of combinational circuits. The only difference is that NAND logic requires a repeated application of De Morgan’s theorem. We shall now demonstrate the derivation of the Boolean function from a logic diagram. Then we will show the derivation of the truth table directly from the NAND logic diagram. Finally, a method will be presented for converting a NAND logic diagram to AND-OR logic diagram by means of block diagram manipulation. Derivation of the Boolean Function by Algebraic Manipulation The procedure for deriving the Boolean function from a logic diagram is outlined in Section 4-6. This procedure is demonstrated for the NAND logic diagram shown in Fig. 4-13, which is the same as that in Fig. 4-11(c). First, all gate outputs are labeled with arbitrary symbols. Second, the Boolean functions for the outputs of gates that receive only external inputs arte derived: T1 = (CD)’ = C’ + D’ T2 = (BC’)’ = B’ C
- 186. 185 The second form follows directly from De Morgan’s theorem and may, at times, be more convenient to use. Third, Boolean functions of gates which have inputs from previously derived functions are determined in consecutive order until the output is expressed in terms of input variables: T3 = (B’T’1)’ = (B’C’ + B’D’)’ = (B + C) (B + D) = B + CD T4 = (AT3)’ = [ A (B + CD)]’ F = (T2 T4)’ = {(BC’)’ [A (B + CD)]’} = BC’ + A(B + CD) Derivation of the Truth Table The procedure for obtaining the truth table directly from a logic diagram is also outlined in Section 4-6. This procedure is demonstrated for the NAND logic diagram of Fig. 4-13. First, the four input variables, together with their 16 combinations of l’s and O’s, are listed as in Table 4-3. Second, the outputs of all gates are labeled with arbitrary symbols as in fig. 4-13. Third, we obtain the truth lable for the putputs of those gates that are a function of the input variables only. These are T’1 and T2, T1 = (CD)’; so we mark O’s in those rows where both C and D are equal to a and fill the rest of the rows of T1 with l’s. Also, T’2 = (BC’)’; so we mark O’s in those rows where B = 1 and C = 0, and fill the rest of the rows of T2, with l’s. We then proceed to obtain the truth table for the outputs of those gates that are a function of previously defined outputs until the columns for the output F is determined. It is now possible to obtain an algebraic
- 187. 186 Table 4.3 Truth Table for Circuit of figure . 4.13 A B C D T1 T2 T3 T4 F 0 0 0 0 1 1 0 1 0 0 0 0 1 1 1 0 1 0 0 0 1 0 1 1 0 1 0 0 0 1 1 0 1 1 1 0 0 1 0 0 1 0 1 1 1 0 1 0 1 1 0 1 1 1 0 1 1 0 1 1 1 1 0 0 1 1 1 0 1 1 1 0 1 0 0 0 1 1 0 1 0 1 0 0 1 1 1 0 1 0 1 0 1 0 1 1 0 1 0 1 0 1 1 0 1 1 0 1 1 1 0 0 1 0 1 0 1 1 1 0 1 1 0 1 0 1 1 1 1 0 1 1 1 0 1 1 1 1 1 0 1 1 0 1 expression for the output from the derived truth table. The map shown in Fig. 4-14 is obtained directly from Table 4-3 and has l’s in the squares of those minterms for which F is equal to 1. The simplified expression obtained from the map is : F = AB + ACD + BC’ = A (B + CD) + BC’ This is the same as the expression of Fig. 4-11, thus verifying the correct answer. Block Diagram Transformation It is sometimes convenient to convert a NAND logic diagram to its equivalent AND-OR logic diagram to facilitate the analysis procedure. By doing so, the Boolean function can be derived more easily without employing De Morgan’s theorem. The conversion of logic diagrams is
- 188. 187 accomplished through a process reverse from that used for implementation. In Section 3-6, we showed two alternate graphic symbols for the NAND gate. These symbols are repeated in Fig. 4-15 for convenience. By judicious use of both symbols, it is possible to convert a NAND diagram to an equivalent AND-OR form. The conversion of a NAND logic diagram to an AND-OR diagram is achieved through a change in symbols from AND invert to invert-OR in alternate levels of gates. The first level to be changed to an invert-OR symbol should be the last level. These changes produce pairs of circles along the same line, and these can be removed since they represent double complementation. Moreover, a one-input AND or OR gate can be removed since it does not perform a logical function. A one-input AND or OR with a circle in the input or output is changed to an inverter circuit. This procedure is demonstrated in Fig. 4-16. The NAND logic diagram of Fig. 4-16(a) is to be converted to an AND-OR diagram. The symbol of the gate in the last level is changed to an invert-OR. Looking for alternate levels, we find one more gate requiring a change of symbol as shown in Fig. 4-16(b). Any two circles along the same line are removed. Circles that go to external inputs are also removed, provided the corresponding input variable is complemented. The required AND-OR logic diagram is drawn in Fig. 4-16(c). MULTILEVEL NOR CIRCUITS The NOR function is the dual of the NAND function. For this reason, all procedures and rules for NOR logic form a dual of the corresponding procedures and rules developed for NAND logic. This section enumerates various methods for NOR logic implementation and analysis by following the same list of topics used for NAND logic. However, less detailed explanation is included so as to avoid excessive repetition of the material in Section 4-7. Universal Gate The NOR gate is universal because any Boolean function can be implemented with it, including a flip-flop circuit as shown in Section 6-2. The conversion of AND, OR and NOT to NOR is shown in Fig. 4-17. The NOT operation is obtained from a one-input NOR gate, yet another symbol for an inverter circuit. The OR operation requires two NOR gates. The first produces
- 189. 188 the inverted-OR and the second acts as an inverter to obtain the normal output. The AND operation is achieved through a NOR gate with additional inverters at each input. Boolean Function Implementation- Block Diagram Method The block diagram procedure for implementing Boolean functions with NOR gates is similar to the procedure outlined in the previous section for NAND gates. 1. Draw the AND-OR logic diagram from the given algebraic expression Assume that both the normal and the complement inputs are available. 1. Draw a second logic diagram with equivalent NOR logic, as given in Fig. 4-17, substituted for each AND, OR and NOT gate. 2. Remove pairs of cascaded inverters from the diagram. Remove inverters connected to single external inputs and complement the corresponding input variable. The procedure is illustrated in Fig. 4-18 for the function: F = A (B + CD) + BC’ The AND-OR implementation of the function is shown in the logic diagram of Fig. 4-18(a). For each OR gate, we substitute a NOR gate followed by an inverter. For each AND gate, we substitute input inverters followed by a NOR gate. The pair of cascaded inverter from the OR box to the AND box is removed. The four inverters connected to external inputs are removed and the input variables complemented. The result is the NOR logic diagram shown in Fig. 4- 18(c). The number of NOR gates in this example equals the number of AND-OR gates plus an additional inverter in the output (NOR gate6). In general, the number of NOR gates required to implement a Boolean function equals the number of AND-OR gates, except for an occasional inverter. This is true provided both normal and complement inputs are available, because the conversion forces certain input variables to be complemented.
- 190. 189 Analysis Procedure The analysis of NOR logic diagrams follows the same procedures presented in Section 4-6 for the analysis of combinational circuits. To derive the Boolean function from a logic diagram, we mark the outputs of various gates with arbitrary symbols. By repetitive substitutions, we obtain the output variable as a function of the input variables. To obtain the truth table from a logic diagram without first deriving the Boolean function, we form a table listing the n in put variables with 2n rows of l’s and O’s. The truth table of various NOR gate outputs is derived in succession until the output truth table is obtained. The output function of a typical NOR gate is of the form T = (A + B’ + C’); so the truth table for T is marked with a O for those combinations where A = 1 or B = O or C = 1. The rest of the rows are filled with l’s. Block Diagram Transformation To convert a NOR logic diagram to its equivalent AND-OR logic diagram, we use the two symbols for NOR gates shown in Fig. 4-19. The OR-invert is the normal symbol for a NOR gate and the invert-AND is a convenient alternative that utilizes De Morgan’s theorem and the convention that small circles at the inputs denote complementation. The conversion of a NOR logic diagram to an AND-OR diagram is achieved through a change in symbols from OR-invert-AND starting from the last level and in alternate levels. Pairs of small circles along the same line are removed. A one-input AND or OR gate is removed, but if it has a small circle at the input or output, it is converted to an inverter. This procedure is demonstrated in Fig. 4-20, where the NOR logic diagram in (a) is converted to an AND-OR diagram. The symbol of the gate in the last level (5) is changed to an invert-AND. Looking for alternate levels, we find one gate in level 3 and two in level 1. These three gates undergo a symbol change as shown in (b). Any two circles along the same line are removed. Circles that go to external inputs are also removed, provided the corresponding input variable is complemented. The gate in level 5 becomes a one-input AND gate and is removed. The required AND-OR logic diagram is drawn in Fig. 4-20(c).
- 191. 190 EXCLUSIVE-OR AND EQUIVALENCE FUNCTIONS Exclusive OR and equivalence, denoted by ⊕ and , respectively, are binary operations that perform the following Boolean functions : x ⊕ y = xy’ + x’y x ⊕ y = xy + x’y’ The two operations are the complements of each other. Each is commutative and associative. Because of these two properties, a function of three or more variables can be expressed without parentheses as follows: (A ⊕ B) ⊕ C = A ⊕ (B ⊕ C) = A ⊕ B ⊕ C This would imply the possibility of using exclusive-OR (or equivalence) gates with three or more inputs. However, multiple-input exclusive-OR gates are very uneconomical from a hardware standpoint. In fact, even a two-input function is usually constructed with other types of gates. For example, Fig. 4-21(a) shows the implementation of a two-input exclusive-OR function with AND, OR and NOT gates, Figure 4-21(b) shows it with NAND gates. Only a limited number of Boolean functions can be expressed exclusively in terms of exclusive-OR or equivalence operations. Nevertheless, these functions emerge quite often during the design of digital systems. The two functions are particularly useful in arithmetic operations and in error detection and correction. An n-variable exclusive-OR expression is equal to the Boolean function with 2”/2 minterms whose equivalent binary numbers have an odd number of l’s. This is demonstrated in the map of Fig. 4-22(a) for the four-variable case. There are 16 minterms for four variables. Half the minterms have a numerical value with an odd number of l’s; the other half have a numerical value with an even number of l’s. The numerical value of a minterm is determined from the row and column numbers of the square that represents the minterm. The map of Fig. 4- 22(a) has l’s in the squares whose minterm numbers have an odd number of l’s. The function can be expressed in terms of the exclusive-OR operations on the four variables. This is justified by the following algebraic manipulation:
- 192. 191 A ⊕ B ⊕ C ⊕ D = (AB’ + A’B) ⊕ (CD’ + C’D) = (AB’ + A’B) (CD “ C’D’) + (AB + A’B’) (CD’ + C’D) = ∑ (1, 2, 4, 7, 8, 11, 13, 14) An n-variable equivalence expression is equal to the Boolean function with 2n/2 minterms, whose equivalent binary numbers have an even number of O’s. This is demonstrated in the map of Fig. 4-22(b) for the four-variable case. The squares with l’s represent the eight minterms with an even number of O’s, and the function can be expressed in terms of the equivalence operations on the four variables. When the number of variables in a function is odd, the minterms with an even number of O’s are the same as the minterms with an odd number of l’s. This is demonstrated in the three- variable map of Fig. 4-23(a). Therefore, an exclusive-OR expression is equal to an equivalence expression when both have the same odd number of variables. However, they form the complements of each other when the number of variables is even, as demonstrated in the two maps of Fig. 4-22(a) and (b). When the minterms of a function with an odd number of variables have an even num er of l’s (or equivalently, an odd number of O’s), the function can be expressed as the complement of either an exclusive-OR or an equivalence expression. For example, the three-variable function shown in the map of Fig. 4-23(b) can be expressed as follows: ( A ⊕ B ⊕ C)’ = A ⊕ B ~ C or ( A ~ B ~ C ) = A ~ B ⊕ C The S output of a full-adder and the D output of a full-subtractor (Section 4-3) can be implemented with exclusive-OR functions because each function consists of four minterms with numerical values having an odd number of l’s. The exclusive-OR function is extensively used in the implementation of digital arithmetic operations because the latter are usually implemented through procedures that require a repetitive addition or subtraction operation. Exclusive-OR and equivalence functions are very useful in systems requiring error- detection and error-correction codes. As discussed in Section 1-6, a parity bit is a scheme for
- 193. 192 detecting errors during transmission of binary information. A parity bit is an extra bit included with a binary message to make the number of l’s either odd or even. The message, including the parity bit, is transmitted and then checked at the receiving end for errors. An error is detected if the checked parity does not correspond to the one transmitted. The circuit that generates the parity bit in the transmitter is called a parity generator; the circuit that checks the parity in the receiver is called a parity checker. As an example, consider a three-bit message to be transmitted with an odd-parity bit. Table 4-4 shows the truth table for the parity generator. The three bits x, y, and z constitute the message and are the inputs to the circuit. The parity bit P is the output. For odd parity, the bit P is generated so as to make the total number of l’s odd (including P). From the truth table, we see that P = 1 when the number of l’s in x, y, and z is even. This corresponds to the map of Fig. 4-23 (b); so the function for P can be expressed as follows: P = x ⊕ y ~ z The logic diagram for the parity generator is shown in Fig. 4-24(a). It consists of one two-input exclusive-OR gate and one two-input equivalence gate. The two gates can be interchanged and still produce the same function, since P is also equal to : P = x ~ y ⊕ z The three-bit message and the parity bit are transmitted to their destination, where they are applied to a parity-checker circuit. An error occurs during transmission if the parity of the four bits received is even, since the binary information transmitted was originally odd. The output C of the parity checker should be a 1 when an error occurs, i.e., when the number of l’s in the four inputs is even. Table 4-5 is the truth table for the odd-parity checker circuit. From it we see that the function for C consists of the eight minterms with numerical values having an even number of O’s. This corresponds to the map of Fig. 4-22(b); so the function can be expressed with equivalence operator as follows: C = x ~ y ~ z ~ P The logic diagram for the parity checker is shown in Fig. 4-24(b) and consists of three two-input equivalence gates.
- 194. 193 It is worth nothing that the parity generator can be implemented with the circuit of Fig. 4- 24(b) if the input P is permanently held at logic-0 and the output is marked P, the advantage being that the same circuit can be used for both parity generator and checking. It is obvious from the foregoing example that parity generation and checking circuits always have an output function that includes half of the minterms whose numerical values have either an even or odd number of l’s. As a consequences, they can be implemented with equivalence and/or exclusive-OR gates. THE LECTURES ON A GO!!!!! 1. Subtractor and half subtractor 2. Derivation of Boolean function by algebraic mnipulation 3. Block dig.transformation 4. Universal gate 5. Exclusive OR and Equivalent function Question: 1. Explain the subtractor and its type? 2. Explain the derivation of the Boolean function by algebraic manipulation? 3. Draw the two symbols of the nand gates? 4. Explain the Boolean function implementation- block diagram method? 5. Explain the Ex-Or gate? 6. I 6.I mplement a full-subtractor with two half-subtractors and an OR gate. References: 1. Computer Systems Architecture --- M.Morris Mano ---Prentice Hall Of India 2.Digital Logic and Computer Design --- M.Morris Mano ---Prentice Hall Of India
- 195. “The lesson content has been compiled from various sources in public domain including but not limited to the internet for the convenience of the users.The university has no proprietary right on the same.” ? Rai Technology University Campus Dhodballapur Nelmangala Road, SH -74, Off Highway 207, Dhodballapur Taluk, Bangalore - 561204 E-mail: info@raitechuniversity.in | Web: www.raitechuniversity.in









































![40
Figure 2.
The positional capability might be provided by one or more small robotic arms, or alternatively
might be provided by any one of a wide range of devices that provide positional control[14]. The
emphasis, though, is on a positional device that is very small in scale: perhaps 0.1 microns (100
nanometers) or so in size.
As an aside, current SPM (Scanning Probe Microscope) designs employ piezoelectric elements
for positional control[21]. A rather obvious question to ask is: why prefer mechanical positioning
systems over piezoelectric or other electrostatic devices? The reasons for using basically
mechanical devices at the molecular scale are similar to the reasons that mechanical devices are
employed at the macroscopic scale: the desire for compactness and high positional accuracy
(e.g., high stiffness). This weighs against electrostatic and piezoelectric devices. Molecular
mechanical devices, on the other hand, can employ very stiff materials and, with appropriate
design, can have joints that can rotate easily but which at the same time provide high stiffness in
other degrees of freedom [1,20]
The "tip chemistry" is logically similar to the ability of the Von Neumann Universal Constructor
to alter the state of a cell at the tip of the arm, but here the change in "state" must correspond to a
real world change in molecular structure. That is, we must specify a set of well defined chemical
reactions that take place at the tip of the arm, and this well defined set of chemical reactions must
be sufficient to allow the synthesis of the class of structures of interest.
The assembler, as defined here, is not a specific device but is instead a class of devices. Specific
members of this class will deal with specific issues in specific ways.](https://image.slidesharecdn.com/advancedcomputerarchitecture-230805214710-1ee6350e/85/Advanced-Computer-Architecture-41-320.jpg)


![43
Lecture 5
ORGANISATION / STRUCTURE /FUNCTION
Objectives of the lecture:
1.To understand the Organisation / Structure /Function
Hello! students, today we will learn about the structure and function of computers. which will
help you to know about about CPU, Registers, Control Unit, ALU, along with this about the
performance factors .
The intent of this lecture is to provide a discussion of the fundamentals of computer organization,
structure and function .
Organization and architecture
In describing computer systems, a distinction is often made between computer architecture and
computer organization. Although it is difficult to give precise definitions for these terms, a
consensus exists about the general areas covered by each (e.g., [VRAN80], [SIEW82], and
[BELL78a].
Computer architecture
™ It refers to those attributes of a system visible to a programmer, or
™ Those attributes that have a direct impact on the logical execution of a program.
• Computer organization
™ It refers to the operational units and their interconnections that realize the architectural
specifications.
• Examples of architectural attributes include ---The instruction set, the number of bits
used to represent various data types (e.g., numbers, characters), I/O mechanisms, and
techniques for addressing memory.
Example Of Organizational attributes include ---Those hardware details transparent to the
programmer, such as control signals, interfaces between the computer and peripherals, and the
memory technology used.
As an example, it is an architectural design issue whether a computer will have a multiply
instruction. It is an organizational issue whether that instruction will be implemented by a special
multiply unit or by a mechanism that makes repeated use of the add unit of the system. The
organizational decision may be based on the anticipated frequency of use of the multiply](https://image.slidesharecdn.com/advancedcomputerarchitecture-230805214710-1ee6350e/85/Advanced-Computer-Architecture-44-320.jpg)
![44
instruction, the relative speed of the two approaches, and the cost and physical size of a special
multiply unit.
Historically, and still today, the distinction between architecture and organization has been an
important one. Many computer manufacturers offer a family of computer models, all with the
same architecture but with differences in organization. Consequently, the different models in the
family have different price and performance characteristics. Furthermore, an architecture may
survive many years, but its organization changes with changing technology. A prominent
example of both these phenomena is the IBM System/370 architecture. This architecture was
first introduced in 1970 and included a number of models. The customer with modest
requirements could buy a cheaper, slower model and, if demand increased, later upgrade to a
more expensive, faster model without having to abandon software that had already been
developed. Over the years, IBM has introduced many new models with improved technology to
replace older models, offering the customer greater speed, lower cost, or both. These newer
models retained the same architecture so that the customer’s software investment was protected.
Remarkably, the System / 370 architecture, with a few enhancements, has survived to this day
and continues as the flagship of IBM’s product life.
In a class of systems called microcomputers, the relationship between architecture and
organization is very close. Changes in technology not only influence organizational but also
result in the introduction of more powerful and richer architectures. Generally, there is less of a
requirement for generation-to-generation compatibility for these smaller machines. Thus, there is
more of an interplay between organizational and architectural design decisions. An intriguing
example of this is the reduced instruction set computer (RISC).
STRUCTURE AND FUNCTION
A computer is a complex system; contemporary computers contain millions of elementary
electronic components. How, then, can one clearly describe them? The key is to recognize the
hierarchic nature of most complex systems, including the computer [SIMO069]. A hierarchic
system is a set of interrelated subsystem, each of the latter, in turn, hierarchic in structure until
we reach some lowest level of elementary subsystem.
The hierarchic nature of complex system is essential to both their design and their description.
The designer need only deal with a particular level of the system at a time. At each level, the
system consists of a set of components and their interrelationships. The behavior at each level
depends only on a simplified, abstracted characterization of the system a the next lower level. At
each level, the designer is concerned with structure and function
Structure : The way in which the components are related.
Function: The operation of each individual component as part of the structure.
FUNCTION:
There are four functions :
1. Data Processing
2. Data Storage](https://image.slidesharecdn.com/advancedcomputerarchitecture-230805214710-1ee6350e/85/Advanced-Computer-Architecture-45-320.jpg)











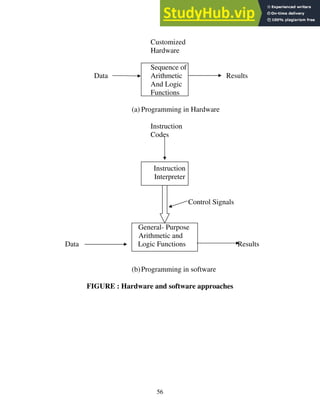
















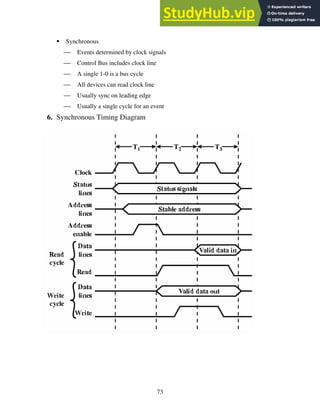








































































![146
-3 = 11-1
= -(0 * 23
+ 0 * 22+
+ 1 * 21
+ 1 * 20
)
= -21
- 20
So this multiplier cannot be used directly in the manner we have been describing.
There are a number of ways out of this dilemma. One would be to convert both multiplier and
multiplicand to positive numbers, perform the multiplication, and then take the two’s
complement of the result if and only if the sign of the two original numbers differed.
Implementers have preferred to use techniques that do not require this final transformation step.
One of the most common of these is Booth’s algorithm [BOOT51]. This algorithm also has the
benefit of speeding up the multiplication process, relative to a more straightforward approach.
Booth’s algorithm is depicted in Figure 8.11 and can be described as follows. As before, the
multiplier and multiplicand are placed in the Q and M registers, respectively. There is also a 1-bit
register placed logically to the right of the least significant bit (Q0) of the register and designated
Q-1; its use is explained shortly. The results of the multiplication will appear in the A and Q
registers. A and Q-1 are initialized to 0. As before, control logic scans the bits of the multiplier
one at a time. Now, as each bit is examined, the bit to its right is also examined. If the two bits
are the same (1-1 or 0-0), then all of the bits of the A, Q, and Q-1 registers are shifted to the right
1 bit. If the two bits differ, then the multiplicand is added to or subtracted from the A register,
according as the two bits are 0-1 or 1-0. Following the addition or subtraction, the right shift
occurs. In either case, the right shift is such that the leftmost bit of A, namely An-1, not only is
shifted into An-2, but also remains in An –1. This is requi9red to preserve the sign of the number
in A and Q. It is known as an arithmetic shift, since it preserves the sign bit.
1001 (9) 1001 (-7)
x0011 (3) x0011 (3)
---------------- ------------------------
00001001 (1001) x 20
11111001 (-7) x 20
+ =(-7)
00010010 (1001) x 21
11110010 (-&) x 21
= (-14)
00011011 (27) 11101011 (-21)
(a) Unsigned Integers (b) Two’s Complement Integers
Fig. Comparison of multiplication of unsigned and two’s complement integers](https://image.slidesharecdn.com/advancedcomputerarchitecture-230805214710-1ee6350e/85/Advanced-Computer-Architecture-147-320.jpg)






































![185
The second form follows directly from De Morgan’s theorem and may, at times, be more
convenient to use. Third, Boolean functions of gates which have inputs
from previously derived functions are determined in consecutive order until the output is
expressed in terms of input variables:
T3 = (B’T’1)’ = (B’C’ + B’D’)’
= (B + C) (B + D) = B + CD
T4 = (AT3)’ = [ A (B + CD)]’
F = (T2 T4)’ = {(BC’)’ [A (B + CD)]’}
= BC’ + A(B + CD)
Derivation of the Truth Table
The procedure for obtaining the truth table directly from a logic diagram is also outlined
in Section 4-6. This procedure is demonstrated for the NAND logic diagram of Fig. 4-13. First,
the four input variables, together with their 16 combinations of l’s and O’s, are listed as in Table
4-3. Second, the outputs of all gates are labeled with arbitrary symbols as in fig. 4-13. Third, we
obtain the truth lable for the putputs of those gates that are a function of the input variables only.
These are T’1 and T2, T1 = (CD)’; so we mark O’s in those rows where both C and D are equal
to a and fill the rest of the rows of T1 with l’s. Also, T’2 = (BC’)’; so we mark O’s in those rows
where B = 1 and C = 0, and fill the rest of the rows of T2, with l’s. We then proceed to obtain
the truth table for the outputs of those gates that are a function of previously defined outputs until
the columns for the output F is determined. It is now possible to obtain an algebraic](https://image.slidesharecdn.com/advancedcomputerarchitecture-230805214710-1ee6350e/85/Advanced-Computer-Architecture-186-320.jpg)








