An Importance Sampling Approach to Integrate Expert Knowledge When Learning Bayesian Networks From Data

An Importance sampling approach to
integrate expert knowledge when learning
Bayesian Networks from data
Andrés Cano, Andrés R. Masegosa and Serafín Moral
Department of Computer Science and Artiﬁcial Intelligence
University of Granada (Spain)
Dortmund, June 2010
Information Processing and Management of Uncertainty in Knowledge-Based Systems
IPMU 2010 Dortmund (Germany) 1/32

Outline
1 Introduction
2 Learning Bayesian Networks(BN) from data
3 Importance Sampling for learning BN
4 Integration of Expert Knowledge
5 Experimental Evaluation
6 Conclusions & Future Works

Introduction
Part I
Introduction

Introduction
Bayesian Networks
Bayesian Networks
Excellent models to graphically represent the dependency structure of the
underlying distribution in multivariate domains.
The learning from data of this dependency structure in a multivariate problem
domain represents a very relevant source of knowledge (direct interactions,
conditional independencies...)

Introduction
Learning Bayesian Networks from Data
Uncertainty in Model Selection
When learning BNs from data there usually are several models with a high
score (high posterior probability given the data).
This situation is specially common in problem domains with high number of
variables and low sample sizes.

Introduction
Integration of Expert Knowledge
Expert Knowledge
In many domain problems expert knowledge is available.
The graphical structure of BNs greatly ease the interaction with a human expert:
Causal ordering.
D-separtion criteria.

Introduction
Expert Knowledge
In many domain problems expert knowledge is available.
The graphical structure of BNs greatly ease the interaction with a human expert:
Causal ordering.
D-separtion criteria.
Previous Works I
There have been many attempts to introduce expert knowledge when learning
BNs from data.
Via Prior Distribution [2,5]: Use of speciﬁc prior distributions over the
possible graph structures to integrate expert knowledge:
Expert assigns higher prior probabilities to most likely edges.

Introduction
Previous Works II
Via structural Restrictions [6]: Expert codify his/her knowledge as structural
restrictions.
Expert deﬁnes the existence/absence of arcs and/or edges and causal
ordering restrictions.
Retrieved model should satisfy these restrictions.

Introduction
Previous Works II
Via structural Restrictions [6]: Expert codify his/her knowledge as structural
restrictions.
Expert deﬁnes the existence/absence of arcs and/or edges and causal
ordering restrictions.
Retrieved model should satisfy these restrictions.
Limitations of "Prior" Expert Knowledge
The system would ask to the expert his/her belief about any possible feature
of the BN (non feasible in high domains).
The expert could be biased to provide the most “easy” or clear knowledge.
The system does not help to the user to introduce information about the BN
structure.

Introduction
Interactive Learning of Bayesian Networks

Introduction
Interactive Learning of Bayesian Networks
Active Interaction with the Expert
Strategy: Ask to the expert by the presence of the edges that most reduce the
model uncertainty.
Method: Framework to allow an efﬁcient and effective interaction with the expert.
Expert is only asked for this controversial structural features.

Previous Knowledge
Part II
Learning Bayesian Networks from data

Previous Knowledge
Notation
Let be X = (X1, ..., Xn) a set of n random variables. Val(Xi ) is the set of values
of Xi .
We assume variables are enumerated in a total causal order.
We also assume a fully observed data set D.

Previous Knowledge
Notation
of Xi .
A Bayesian Network B can be described by:
G the graph structure.
θG the parameters.
A graph G can be decomposed as a vector of parent sets:
G = (Pa(X1), ..., Pa(Xn))

Previous Knowledge
Notation
of Xi .
A Bayesian Network B can be described by:
G the graph structure.
θG the parameters.
A graph G can be decomposed as a vector of parent sets:
G = (Pa(X1), ..., Pa(Xn))
We also deﬁne Ui as a random variable taking values in the space of all possible
parent sets of Xi , Val(Ui ).
Let be G a random variable taking values in the set Val(G) of all possible graph
structures consistent with the total order.

Previous Knowledge
The Bayesian Learning Framework
Scoring a graph structure
Marginal Likelihood of a graph structure:
P(G = G|D) = P(G|D) ∝ P(G)P(D|G) =
i
score(Xi , PaG(Xi )|D)
scoreBDeu(Xi , Ui |D) = Pi (U)
|Ui |
j=0
Γ(αij )
Γ(αij + Nij )
|Xi |
k=1
Γ(αijk + Nijk )
Γ(αijk )
Pi (U) is the prior probability that U is the parent set of Xi .
Approximating the posterior P(G|D)
Our approach is supported on the approximation of P(G|D).
It allows to know which graph structures are the most likely (best explain the
data).
Exhaustive enumeration is not feasible because the space of graph structures is
super-exponential.

Previous Knowledge
Approximating the Posterior
Factorization of P(G|D)
Assumption of a total order implies that the selection of the parent sets for
each Xi are independent among them:
P(G|D) =
i
P(Ui |D)
P(G|D) can be decomposed in n independent problems.
P(Ui |D) posterior probability of the possible parent sets of variable Xi .
Each of the sub-problems still has exponential size.

Previous Knowledge
Approximating the Posterior P(Ui|D)
Closed Form Solution
In [3] it was proposed a closed form solution assuming a node can have up to
K parents.
It would have a polynomial efﬁciency O(n(K+1)).

Previous Knowledge
Approximating the Posterior P(Ui|D)
Closed Form Solution
In [3] it was proposed a closed form solution assuming a node can have up to
K parents.
It would have a polynomial efﬁciency O(n(K+1)).
Markov Chain Monte Carlo
Lets Val(Ui ) be the space model of the Markov Chain.
If the Markov Chain is in some state U in iteration t, a new model U is
randomly drawn by adding, deleting of switching any edge.
The Markov Chain moves to state U in the iteration t + 1 with probability:
m(Ut
, Ut+1
) = min{1,
N(U)score(D|U )
N(U )score(D|U)
}
If it not, the Markov Chain remains in state U.
This Markov Chain has an stationary distribution (t → ∞) which is P(U|D).

Importance Sampling
Part III
Importance Sampling

Importance Sampling
Importance Sampling
Description
Based on the employment of an auxiliary distribution Q which roughly
approximate P, the target distribution.
Q is a distribution which is easier to sample for it.
EP (f(x)) =
P(x)
Q(x)
f(x)Q(x)dx = EQ(w(x)f(x)) (1)
where w(x) =
P(x)
Q(x)
acts as a weight function.

Importance Sampling
Importance Sampling
Description
Based on the employment of an auxiliary distribution Q which roughly
approximate P, the target distribution.
Q is a distribution which is easier to sample for it.
EP (f(x)) =
P(x)
Q(x)
f(x)Q(x)dx = EQ(w(x)f(x)) (1)
where w(x) =
P(x)
Q(x)
acts as a weight function.
A set of T samples {x1, ..., xT } are generated form Q and, then, it is computed
wt =
P(xt
)
Q(xt )
.
The estimator ˆµ of EP (f(x)) is ﬁnally computed as follows:
ˆµ =
T
t=1 w(xt )f(t)
T
t=1 w(xt )
(2)
Key Aspect: P and Q can be known up to a multiplicative constant.

Importance Sampling
Importance Sampling for learning BNs
Step 0:
Candidate Parents are considered in a
random permutation.
Score of initial model:
score(X, {∅}|D)

Importance Sampling
Step 1:
Evaluate C as parent of X.
Compute the ratio:
r =
score(X, {C}|D)
score(X, {C}|D) + score(X, {∅}|D)
= 0.8
Randomly accept C as parent of X with probability
r = 0.8 −→ Accepted.
Q = 0.8

Importance Sampling
Step 2:
Evaluate B as parent of X.
Compute the ratio:
r =
score(X, {C, B}|D)
score(X, {C, B}|D) + score(X, {C}|D)
= 0.1
Randomly accept B as parent of X with probability
r = 0.1 −→ Non Accepted.
Q = 0.8 · 0.9

Importance Sampling
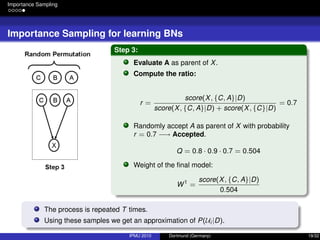
Step 3:
Evaluate A as parent of X.
Compute the ratio:
r =
score(X, {C, A}|D)
score(X, {C, A}|D) + score(X, {C}|D)
= 0.7
Randomly accept A as parent of X with probability
Q = 0.8 · 0.9 · 0.7 = 0.504
Weight of the ﬁnal model:
W1
=
score(X, {C, A}|D)
0.504

Importance Sampling
Step 3:
Evaluate A as parent of X.
Compute the ratio:
r =
score(X, {C, A}|D)
score(X, {C, A}|D) + score(X, {C}|D)
= 0.7
Randomly accept A as parent of X with probability
Q = 0.8 · 0.9 · 0.7 = 0.504
Weight of the ﬁnal model:
W1
=
score(X, {C, A}|D)
0.504
The process is repeated T times.
Using these samples we get an approximation of P(Ui |D).

Integrating Expert Knowledge
Part IV

Methodology Description

Prior Knowledge
Representing absence of prior knowledge
“Uniform prior over structures is usually chosen by convenience” [3].
P(G) does not grow with the data, but it matters at low sample sizes.

Prior Knowledge
Let us assume that the prior probability of an edge is p and independent of
each other. If Xi has k parents out of m nodes:
P(Pa(Xi )) = pk
(1 − p)(m−k)
If the number of candidate parents m grows, p should be decreased to
control de number of false positives edges: “multiplicity correction”.

Prior Knowledge
Let us assume that the prior probability of an edge is p and independent of
each other. If Xi has k parents out of m nodes:
P(Pa(Xi )) = pk
(1 − p)(m−k)
If the number of candidate parents m grows, p should be decreased to
control de number of false positives edges: “multiplicity correction”.
This is solved by assuming that p has a Beta prior with parameter α = 0.5 [11]:
Pi (Pa(Xi )) =
Γ(2 ∗ α)
Γ(m + 2α)
Γ(k + α)Γ(m − k + α)
Γ(α)Γ(α)

Interacting with the Expert
Description
Key Idea: As lower the entropy of P(Ui |D) is, more reliable learning we have.
Expert Interaction is carried out in order to reduce the entropy H(P(Ui |D)).
.

P(S → X|D) = 0.85 P(R → X|D) = 0.8 P(C → X|D) = 0.45
Description
Key Idea: As lower the entropy of P(Ui |D) is, more reliable learning we have.
Expert Interaction is carried out in order to reduce the entropy H(P(Ui |D)).
System ask to the expert by those edges with higher entropy.

P(S → X|D) = 0.88 P(R → X|D) = 0.77 P(C → X|D) = 1.0
Description
The entropy of P(Ui |D) is reduced. Probability mass concentrates around
one model.
This methodology can be iteratively applied asking by the presence/absence
of more edges.
Stopping the interaction when the probability of MAP model is L times higher
the second most probable model.

Experimental Evaluation
Part V

Experimental Set-up
Bayesian Networks:
alarm (37 nodes), boblo (23 nodes), boerlage-92 (23 nodes), hailﬁnder (56
nodes), insurance (27 nodes).
Sample Sizes:
We run 10 times the algorithms with different samples sizes: 50, 100, 500
and 1000.

Experimental Set-up
Bayesian Networks:
alarm (37 nodes), boblo (23 nodes), boerlage-92 (23 nodes), hailﬁnder (56
nodes), insurance (27 nodes).
Sample Sizes:
We run 10 times the algorithms with different samples sizes: 50, 100, 500
and 1000.
Evaluation Measures
Number of missing/extra links, Kullback-Leibler distance...
We report average values across the ﬁve networks.
Expert Interaction is simulated:
Access to the true BN model when asking by
presence/absence of an edge.

Structure Prior Evaluation
N. of Structural Errors KL Distance
Analysis
Beta-Prior reduces the number of structural errors for both IS and MCMCM.
IS has a low number of errors than MCMC specially with low sample sizes.
Beta-Prior also reduces KL distance for both IS and MCMC.

Expert Interaction Evaluation
N. of Structural Errors KL Distance
Analysis
As much the mass of the posterior probability is concentrated around one model,
the lower is the number of structural errors.
The KL distance does not signiﬁcantly improve with large sample sizes (these
structural errors do not have great impact in the prediction capacity).

Expert Interaction Evaluation
N. of Interactions Interaction Accuracy
Analysis
The number of Interactions are feasible for a human expert.
Prior Exhaustive Querying: 600 questions in averaged.
The Interaction Accuracy: ratio between number of reduced structural
errors and number of interactions.
Average Accuracy of random interactions: 1%.

Conclusions
Part VI
Conclusions & Future Works

Conclusions
Conclusions
A new methodology to introduce expert knowledge when
learning BN from data.
A new Importance sampling technique for sampling BN.
System requests to the expert a feasible number of questions.
Interaction improves the quality of the inferred BN models.

Conclusions
Conclusions
A new methodology to introduce expert knowledge when
learning BN from data.
A new Importance sampling technique for sampling BN.
System requests to the expert a feasible number of questions.
Interaction improves the quality of the inferred BN models.
Future Works
Extend these methods to the learning of BN models without
causal ordering assumptions.

Thanks for your attention!!
Questions?

An Importance Sampling Approach to Integrate Expert Knowledge When Learning Bayesian Networks From Data

More Related Content

What's hot (20)

Viewers also liked (9)

Similar to An Importance Sampling Approach to Integrate Expert Knowledge When Learning Bayesian Networks From Data (20)

More from NTNU (17)

Recently uploaded (20)

An Importance Sampling Approach to Integrate Expert Knowledge When Learning Bayesian Networks From Data