BAB LP metode simplex operation research
- 1. PROGRAM LINIER – METODE SIMPLEKS
- 2. ◾ Merupakan metode yang biasanya digunakan untuk memecahkan setiap permasalahan pada pemrogramman linear yang kombinasi variabelnya terdiri dari tiga variabel atau lebih. ◾ Metode yang secara matematis dimulai dari pemecahan dasar yang feasibel (basic feasible solution) ke pemecahan dasar feasibel lainnya, yang dilakukan berulang-ulang (iteratif) sehingga
- 3. ◾ Diperkenalkan pada tahun 1947 oleh George B. Dantzig dan telah diperbaiki oleh beberapa ahli lain. ◾ Metode penyelesaian dari Metode Simpleks ini melalui perhitungan ulang (iteration) di mana langkah- langkah perhitungan yang sama diulang-ulang sampai solusi optimal diperoleh.
- 4. Syarat : Model program linier (Canonical form) harus dirubah dulu ke dalam suatu bentuk umum yang dinamakan ”bentuk baku” (standard form). Sifat bentuk baku: ◾ Semua batasan adalah persamaan (dengan tidak ada nilai negatif pada sisi kanan) ◾ Semua variabel tidak ada yang bernilai negatif, dan ◾ Fungsi tujuan dapat berupa
- 5. 1 Maksimalkan/minimalkan: 𝑧 𝑥1, 𝑥2, … … , 𝑥𝑛 = σ 𝑛 𝑐𝑗𝑥𝑗 1 dengan batasan (kendala): σ 𝑛 𝑎𝑖𝑗𝑥𝑗 ≤ ≥ 𝑏 𝑖 𝑑𝑎𝑛 𝑥𝑗 ≥ 0 𝑑𝑒𝑛𝑔𝑎𝑛 𝑖 = 1,2,3, … 𝑚 𝑑𝑎𝑛 𝑗 = 1,2,3, … 𝑛 Atau Maksimalkan/minimalkan: 𝑧 = 𝑐1 𝑥1 + 𝑐2 𝑥2 + 𝑐3 𝑥3 + ⋯ . . +𝑐𝑛 𝑥𝑛 dengan batasan(kendala): 𝑎11 𝑥1 + 𝑎12 𝑥2 + 𝑎13 𝑥3 + ⋯ … + 𝑎1𝑛 𝑥𝑛 ≤ 𝑎𝑡𝑎𝑢 ≥ 𝑏1 𝑎21 𝑥1 + 𝑎22 𝑥2 + 𝑎23 𝑥3 + ⋯ … + 𝑎2𝑛 𝑥𝑛 ≤ 𝑎𝑡𝑎𝑢 ≥ 𝑏2 … . . 𝑎𝑚 1𝑥1 + 𝑎𝑚 2𝑥2 + 𝑎𝑚 3 𝑥3 + ⋯ … + 𝑎𝑚 𝑛 𝑥𝑛 ≤
- 6. z = Fungsi tujuan xj = Jenis kegiatan (variabel keputusan) aij = Kebutuhan sumberdaya i untuk menghasilkan setiap unit kegiatan j bi = Jumlah sumberdaya i yang tersedia cj = Kenaikan nilai Z jika ada pertambahan satu unit kegiatan j a, b, dan c, disebut juga sebagai parameter model m = Jumlah sumberdaya yang tersedia n = Jumlah kegiatan.
- 7. ◾ Fungsi Pembatas Suatu fungsi pembatas yang mempunyai tanda < diubah menjadi suatu bentuk persamaan (bentuk standar) dengan cara menambahkan suatu variabel baru yang dinamakan slack variable . Banyaknya slack variable bergantung pada fungsi pembatas.
- 8. ◾ Fungsi Tujuan Dengan adanya slack variable pada fungsi pembatas, maka fungsi tujuan juga harus disesuaikan dengan memasukkan unsur slack variable ini. Karena slack variable tidak mempunyai kontribusi apa-apa terhadap fungsi tujuan, maka konstanta untuk slack variable tersebut dituliskan nol.
- 10. ◾ Setelah fungsi batasan diubah ke dalam bentuk persamaan (bentuk standar), maka untuk menyelesaikan masalah program linier dengan metode simpleks menggunakan suatu kerangka tabel yang disebut dengan tabel simpleks. ◾ Tabel ini mengatur model ke dalam suatu bentuk yang memungkinkan untuk penerapan penghitungan matematis
- 11. Var. Dasar Z X1 X2 . . . . Xn S1 S2 . . . . Sn NK Z 1 -C1 -C2 . . . . -Cn 0 0 0 0 0 S1 0 a11 a12 . . . a1n 1 0 0 0 b1 S2 0 a21 a22 . . . a2n 0 1 0 0 b2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Sn 0 am1 am2 . . . amn 0 0 0 1 bm
- 12. 1. Rumuskan persoalan PL ke dalam model umum PL (fungsi tujuan dan fungsi pembatas). 2. Ubah model umum PL menjadi model simpleks: a. Fungsi Pembatas: tambahkan slack variable (surplus variabel, variabel buatan atau artifisial variable)
- 13. b. Fungsi tujuan : - Ubahlah bentuk fungsi tujuan eksplisit menjadi persamaan bentuk implisit - Tambahkan/kurangi dengan slack variable (surplus var atau variable buatan) yang bernilai nol. 3. Formulasikan ke dalam Tabel Simpleks. 4. Lakukan langkah-
- 14. ◾ Model Program Linear 1. Fungsi Tujuan : Maksimumkan : Z=8X1 + 6X2 (dalam Rp 1000) 2.Fungsi Pembatas : Bahan A : 4X1 + 2X2 ≤ 60 Bahan B : 2X1 + 4X2 ≤ 48 X1, X2 ≥ 0
- 15. ◾ Model Simpleks : 1.Fungsi Tujuan : Maksimumkan Z– 8X1–6 X2–0S1- 0S2 = 0 2. Fungsi Pembatas : 4X1+2X2+ S1+ 0S2 = 60 2X1+4X2+0S1+ S2 = 48
- 16. Variabel Dasar X1 X2 S1 S2 NK Z S1 S2
- 17. Variabel Dasar X1 X2 S1 S2 NK Z -8 -6 0 0 0 S1 S2
- 18. Variabel Dasar X1 X2 S1 S2 NK Z -8 -6 0 0 0 S1 4 2 1 0 60 S2
- 19. Variabel Dasar X1 X2 S1 S2 NK Z -8 -6 0 0 0 S1 4 2 1 0 60 S2 2 4 0 1 48
- 20. Variabel Dasar X1 X2 S1 S2 NK Z -8 -6 0 0 0 S1 4 2 1 0 60 S2 2 4 0 1 48 1. Iterasi Awal (Iterasi- 0)
- 21. Variabel Dasar X1 X2 S1 S2 NK Z -8 -6 0 0 0 S1 4 2 1 0 60 S2 2 4 0 1 48 2. Iterasi-1 : a. Menentukan kolom kunci : kolom yang mempunyai koefisien fungsi tujuan yang bernilai negatif terbesar.
- 22. Variabel Dasar X1 X2 S1 S2 NK Indeks Z -8 -6 0 0 0 - S1 4 2 1 0 60 15 S2 2 4 0 1 48 24 b. Menentukan baris kunci : nilai indeks yang terbesar (positif). 𝑁𝐾 𝐹𝑢𝑛𝑔𝑠𝑖 𝑃𝑒𝑚𝑏𝑎𝑡𝑎𝑠 𝑁𝑖𝑙𝑎𝑖 𝐼𝑛𝑑𝑒𝑘𝑠 = 𝑁𝑖𝑙𝑎𝑖 𝐾𝑜𝑙𝑜𝑚 𝐹. 𝑃𝑒𝑚𝑏𝑎𝑡𝑎𝑠 Angka Kunci
- 23. Variabel Dasar X1 X2 S1 S2 NK Z X1 1 ½ ¼ 0 15 S2 c. Perubahan-perubahan nilai baris : - Nilai baris kunci baru = (Nilai baris kunci lama) / n-angka kunci - Nilai baris yang lain = Baris lama – {(Nilai baris kunci baru) x (angka kolom kunci baris ybs)}
- 24. [-8 -6 0 0 0 ] (-8) [ 1 1/2 1/4 0 15 ] ( - ) Nilai baru = [0 -2 2 0 120 ] Mengubah nilai-nilai selain pada baris kunci Rumus : Baris baru = baris lama – (koefisien pada kolom kunci) x nilai baru baris kunci Baris pertama (Z) Baris ke-3 (batasan 2) [2 4 0 1 48 ] (2) [ 1 1/2 1/4 0 15 ] ( - ) Nilai baru = [0 3 -1/2 1 18 ] Langkah Penyelesaian (5)
- 25. Variabel Dasar X1 X2 S1 S2 NK Z 0 - 2 2 0 120 X1 1 ½ ¼ 0 15 S2 0 3 - ½ 1 18
- 26. Variabel Dasar X1 X2 S1 S2 NK Indeks Z 0 - 2 2 0 120 - X1 1 ½ ¼ 0 15 30 S2 0 3 - ½ 1 18 6
- 27. Variabel Dasar X1 X2 S1 S2 NK Indeks Z X1 X2 0 1 - 1/6 1/3 6 -
- 28. (0 - 2 2 0 120) (-2) (0 1 - 1/6 1/3 6) ( - ) Nilai baru = 0 0 5/3 2/3 132 Mengubah nilai-nilai selain pada baris kunci Rumus : Baris baru = baris lama – (koefisien pada kolom kunci) x nilai baru baris kunci Baris pertama (Z) Baris ke-2 (batasan 1) (1 ½ ¼ 0 15) (1/2) (0 1 - 1/6 1/3 6) ( - ) Nilai baru = 1 0 1/3 -1/6 12
- 29. Variabel Dasar X1 X2 S1 S2 NK Indeks Z 0 0 5/3 2/3 132 - X1 1 0 1/3 - 1/6 12 - X2 0 1 - 1/6 1/3 6 -
- 30. Pada iterasi-2 terlihat bahwa koefisien fungsi tujuan sudah tidak ada lagi yang mempunyai nilai negatif, proses perubahan selesai dan ini menunjukkan penyelesaian persoalan linear dengan metode simpleks sudah mencapai optimum dengan hasil sbb : X1= 12 dan X2 = 6 dengan Zmakasimum = Rp 132.000.-
- 31. ◾ Model Program Linear 1. Fungsi Tujuan : Maksimumkan : Z=15X1 + 10X2 (Dlm Rp10.000) 2. Fungsi Pembatas : Bahan A : X1 + X2 ≤ 600 Bahan B : 2X1 + X2 ≤
- 32. 1. Fungsi Tujuan : Maksimumkan Z– 15X1– 10 X2–0S1- 0S2 = 0 2.Fungsi Pembatas : X1+X2+ S1+ 0S2 = 600 2X1+X2+0S1+ 1S2 = 1000 X1, X2, S1, S2 ≥ 0
- 33. Variabel Dasar X1 X2 S1 S2 NK Z S1 S2
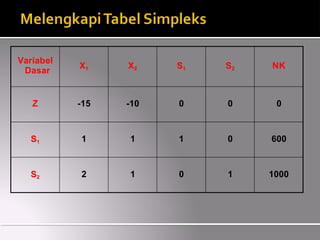
- 34. Variabel Dasar X1 X2 S1 S2 NK Z -15 -10 0 0 0 S1 S2
- 35. Variabel Dasar X1 X2 S1 S2 NK Z -15 -10 0 0 0 S1 1 1 1 0 600 S2
- 36. Variabel Dasar X1 X2 S1 S2 NK Z -15 -10 0 0 0 S1 1 1 1 0 600 S2 2 1 0 1 1000
- 37. Variabel Dasar X1 X2 S1 S2 NK Z -15 -10 0 0 0 S1 1 1 1 0 600 S2 2 1 0 1 1000 1. Iterasi Awal (Iterasi- 0)
- 38. Variabel Dasar X1 X2 S1 S2 NK Z -15 -10 0 0 0 S1 1 1 1 0 600 S2 2 1 0 1 1000 2. Iterasi- 1 : a. Menentukan kolom kunci : kolom yang mempunyai koefisien fungsi tujuan yang bernilai negatif terbesar.
- 39. Variabel Dasar X1 X2 S1 S2 NK Indeks Z -15 -10 0 0 0 - S1 1 1 1 0 600 600 S2 2 1 0 1 1000 500 b. Menentukan baris kunci : nilai indeks yang terbesar (positif). 𝑁𝐾 𝐹𝑢𝑛𝑔𝑠𝑖 𝑃𝑒𝑚𝑏𝑎𝑡𝑎𝑠 𝑁𝑖𝑙𝑎𝑖 𝐼𝑛𝑑𝑒𝑘𝑠 = 𝑁𝑖𝑙𝑎𝑖 𝐾𝑜𝑙𝑜𝑚 𝐹. 𝑃𝑒𝑚𝑏𝑎𝑡𝑎𝑠
- 40. Variabel Dasar X1 X2 S1 S2 NK Z S1 X1 1 ½ 0 ½ 500 c. Perubahan-perubahan nilai baris : - Nilai baris kunci baru = (Nilai baris kunci lama) / n-angka kunci - Nilai baris yang lain = Baris lama – (Nilai baris kunci baru) x angka kolom kunci baris ybs.
- 41. Variabel Dasar X1 X2 S1 S2 NK Z S1 0 ½ 1 - ½ 100 X1 1 ½ 0 ½ 500 c. Perubahan-perubahan nilai baris : - Nilai baris kunci baru = (Nilai baris kunci lama) / n-angka kunci - Nilai baris yang lain = Baris lama – (Nilai baris kunci baru) x angka kolom kunci baris ybs.
- 42. Variabel Dasar X1 X2 S1 S2 NK Z 0 -2½ 0 7½ 7500 S1 0 ½ 1 - ½ 100 X1 1 ½ 0 ½ 500
- 43. 3. Iterasi-2 : perhatikan apakah koefisien fungsi tujuan pada Tabel simpleks masih ada yang bernilai negatif. Angka Kunci Variabel Dasar X1 X2 S1 S2 NK Indeks Z 0 -2½ 0 7½ 7500 - S1 0 ½ 1 - ½ 100 200 X1 1 ½ 0 ½ 500 1000
- 44. Variabel Dasar X1 X2 S1 S2 NK Indeks Z X2 0 1 2 -1 200 - X1
- 45. Variabel Dasar X1 X2 S1 S2 NK Indeks Z X2 0 1 2 -1 200 - X1 1 0 -1 1 400 -
- 46. Variabel Dasar X1 X2 S1 S2 NK Indeks Z 1 0 5 5 8000 - X2 0 1 2 -1 200 - X1 1 0 -1 1 400 -
- 47. Pada iterasi-2 terlihat bahwa koefisien fungsi tujuan sudah tidak ada lagi yang mempunyai nilai negatif, proses peru- bahan selesai dan ini menunjukkan penyelesaian persoalan linear dengan metode simpleks sudah mencapai optimum dengan hasil sbb : X1= 400 dan X2 = 200 dengan Zmakasimum = Rp 8000.-
- 48. ◾ Model Program Linear Fungsi Tujuan : Maksimumkan : Z = 3X1+2X2 Fungsi Pembatas : X1 + X2 ≤ 15 2X1 + X2 ≤ 28 X1 + 2X2 ≤ 20 X1, X2 ≥ 0
- 49. ◾ Model Simpleks Fungsi Tujuan : Maksimumkan Z– X1–2X1–0S1–0S2–0S3 = 0 Fungsi Pembatas : X1 + X2 + S1 2X1 + X2 + S2 X1 + 2X2 = 15 = 28 + S3 = 20 X1, X2 ≥ 0
- 50. Variabel Dasar X1 X2 S1 S2 S3 NK Z S1 S2 S3 Tabel Simpleks
- 51. Variabel Dasar X1 X2 S1 S2 S3 NK Z -3 -2 0 0 0 0 S1 S2 S3
- 52. Variabel Dasar X1 X2 S1 S2 S3 NK Z -3 -2 0 0 0 0 S1 1 1 1 0 0 15 S2 S3
- 53. Variabel Dasar X1 X2 S1 S2 S3 NK Z -3 -2 0 0 0 0 S1 1 1 1 0 0 15 S2 2 1 0 1 0 28 S3
- 54. Variabel Dasar X1 X2 S1 S2 S3 NK Z -3 -2 0 0 0 0 S1 1 1 1 0 0 15 S2 2 1 0 1 0 28 S3 1 2 0 0 1 20
- 55. Variabel Dasar X1 X2 S1 S2 S3 NK Indeks Z -3 -2 0 0 0 0 - S1 1 1 1 0 0 15 15 S2 2 1 0 1 0 28 14 S3 1 2 0 0 1 20 20
- 56. Variabel Dasar X1 X2 S1 S2 S3 NK Indeks Z -3 -2 0 0 0 0 - S1 1 1 1 0 0 15 15 S2 2 1 0 1 0 28 14 S3 1 A ngka2Ku nc i 0 0 1 20 20
- 57. Variabel Dasar X1 X2 S1 S2 S3 NK Indeks Z S1 X1 1 ½ 0 ½ 0 14 - S3
- 58. Variabel Dasar X1 X2 S1 S2 S3 NK Indeks Z S1 X1 1 ½ 0 ½ 0 14 - S3 0 3/2 0 -½ 1 6 -
- 59. Variabel Dasar X1 X2 S1 S2 S3 NK Indeks Z S1 0 ½ 1 -½ 0 1 - X1 1 ½ 0 ½ 0 14 - S3 0 3/2 0 -½ 1 6 -
- 60. Variabel Dasar X1 X2 S1 S2 S3 NK Indeks Z 0 -½ 0 3/2 0 42 - S1 0 ½ 1 -½ 0 1 - X1 1 ½ 0 ½ 0 14 - S3 0 3/2 0 -½ 1 6 -
- 61. Variabel Dasar X1 X2 S1 S2 S3 NK Indeks Z 0 -½ 0 3/2 0 42 - S1 0 ½ 1 -½ 0 1 2 X1 1 ½ 0 ½ 0 14 28 S3 0 3/2 0 -½ 1 6 4
- 62. Variabel Dasar X1 X2 S1 S2 S3 NK Indeks Z X2 0 1 2 -1 0 2 - X1 S3
- 63. Variabel Dasar X1 X2 S1 S2 S3 NK Indeks Z X2 0 1 2 -1 0 2 - X1 1 ½ 0 ½ 0 14 - S3
- 64. Variabel Dasar X1 X2 S1 S2 S3 NK Indeks Z X2 0 1 2 -1 0 2 - X1 1 ½ 0 ½ 0 14 - S3 0 0 0 -3 1 1 -
- 65. Variabel Dasar X1 X2 S1 S2 S3 NK Indeks Z 0 0 1 1 0 43 - X2 0 1 2 -1 0 2 - X1 1 ½ 0 ½ 0 14 - S3 0 0 0 -3 1 1 -
- 66. Pada iterasi-2 terlihat bahwa koefisien fungsi tujuan sudah tidak ada lagi yang mempunyai nilai negatif, proses peru- bahan selesai dan ini menunjukkan penyelesaian perhitungan persoalan program linear simpleks sudah mencapai denga n optimu m metod e denga n rincian sbb : X1 =13; X2=2, dengan Zmaksimum = 43
- 67. Maksimumkan Z = 60X1+30X2+20X3 Dengan Pembatas : 8X1 + 6X2 + X3 ≤ 48 4X1 + 2X2 + 1.5X3 ≤ 20 2X1 + 1.5X2 + 0.5X3 ≤ 8 X2 ≤ 5 X1,X2,x3 ≥
- 68. Maksimum z = 8 x1 + 9 x2 + 4x3 Dengan Pembatas : x1 + x2 + 2x3 ≤ 2 2x1 + 3x2 + 4x3 ≤ 3 7x1 + 6x2 + 2x3 ≤ 8 x1,x2,x3 ≥ 0
- 69. Memaksimumka n z = 8 x1 + 7 x2 + 3x3 Dengan Pembatas : x1 + x2 + 2x3 ≤ 4 2x1 + 3x2 + 4x3 ≤ 7 3x1 + 6x2 + 2x3 ≤ 8
- 70. Penyimpanganbentuk standar dapat terjadi karena : 1. Fungsi tujuan (Z) bukan Maximalisasi, tetapi Minimalisasi 2. Fungsi batasan bertanda (=) atau ( ) ≥ 3. Dan syarat X1 atau X2 tidak terpenuhi, misalkan X1 ≥ - 10 (negatif)
- 71. Fungsi Tujuan : Minimalkan Z = 3X1 + 5X2 2X1 = 8 3X2 ≤ 15 Dengan batasan : Mesin A Mesin B Mesin C 6X1 + 5X2 ≥ 30 , di mana X1 dan X2 ≥ 0
- 72. ◾ Fungsi tujuan agar menjadi maksimal dikalikan dengan (-1) ◾ Jika kendala bertanda “=“, tambahkan ruas kiri satu variabel tambahan berupa variabel artifisial . ◾ Jika kendala bertanda “>”, kurangkan ruas kiri dgn variabel surplus dan tambahkan juga ruas kiri dgn variabel artifisial. ◾ Masukkan / tambahkan pula variabel-variabel surplus dan artifisial ke dalam fungsi tujuan, dimana koefisien untuk var. surplus = 0 dan koefisien var.
- 73. ◾ Minimalkan Z = 3X1 + 5X2 menjadi Maksimalkan (- Z) ◾ Mesin A 2X1 = -3X1 – 5X2 = 8, akan menjadi : 2X1 + X3 3X2 ≤ 15 = 8 3X2 + X4 = 15 ◾ Mesin B ◾ Mesin C 6X1 + 5X2 ≥ 30 , akan menjadi 6X1 + 5X2 -X5 + X6 = 30 Sehingga fungsi tujuan menjadi : Maksimal : –Z + 3X1 + 5 X2 + MX3 + MX6 = 0 Indrawani Sinoem/TRO/SI- 5
- 74. Masalah berikutnya yang muncul adalah setiap variabel dasar (slack atau artificial variabel), harus bernilai nol, sehingga MX3 dan MX6 di atas harus di-nol-kan terlebih dahulu, sebelum dipindah ke digunakan tabel simplex. Carayang adalah dengan menguran gi bilangan M tersebut dengan bilangan M itu sendir i, setiap yang sebelumnya dikalikan dengan nilai batasan yang menyebabkan munculnya bilangan M tersebut.
- 75. Nilai fungsi tujuan terakhir adalah : 3 5 M 0 0 M 0 ◾ Kita coba hilangkan M yang pertama terlebih dahulu. ◾ X1 X2 X3 X4 X5 X6 NK ◾ 3 5 M 0 0 M 0 ( 2 0 1 0 0 0 8 ) M _____________________________________ - 3-2M 5 0 0 0 M -8M
- 76. ◾ Selanjutnya kita hilangkan M yang kedua. ◾ 3-2M 5 0 0 0 M -8M ( 6 5 0 0 -1 1 30 ) x M ________________________________________________- 3-8M 5-5M 0 0 M 0 -38M, Atau ◾ -8M+3 -5M+5 0 0 M 0 -38M Yang merupakan nilai dari fungsi tujuan yang baru selanjutnya akan dimasukkan ke tabel simplex, sehingga tabel simlex awalnya adalah sebagai berikut :
- 77. X1 X2 X3 X4 X5 X6 NK Z -8M+3 -5M+5 0 0 M 0 -38M X3 2 0 1 0 0 0 8 X4 0 3 0 1 0 0 15 X6 6 5 0 0 -1 1 30 Tabel Awal simplex, untuk kasus penyimpangan :























![[-8 -6 0 0 0 ]
(-8) [ 1 1/2 1/4 0 15 ] ( - )
Nilai baru = [0 -2 2 0 120 ]
Mengubah nilai-nilai selain pada baris kunci
Rumus :
Baris baru = baris lama – (koefisien pada kolom kunci) x nilai baru baris
kunci
Baris pertama (Z)
Baris ke-3 (batasan
2) [2 4 0 1 48 ]
(2) [ 1 1/2 1/4 0 15 ] ( - )
Nilai baru = [0 3 -1/2 1 18 ]
Langkah Penyelesaian
(5)](https://image.slidesharecdn.com/bab3-lpmetodesimplex-241024083149-df19786c/85/BAB-LP-metode-simplex-operation-research-24-320.jpg)