Carry look ahead adder
- 2. Carry Lookahead Adder Most other arithmetic operations, e.g. multiplication and division are implemented using several add/subtract steps. Thus, improving the speed of addition will improve the speed of all other arithmetic operations. Accordingly, reducing the carry propagation delay of adders is of great importance. Different logic design approaches have been employed to overcome the carry propagation problem. One widely used approach employs the principle of carry look-ahead solves this problem by calculating the carry signals in advance, based on the input signals.
- 3. CLA -Continued A carry-lookahead adder (CLA) or fast adder is a type of adder used in digital logic. A carry-lookahead adder improves speed by reducing the amount of time required to determine carry bits. : Calculating, for each digit position, whether that position is going to propagate a carry if one comes in from the right. Combining these calculated values to be able to deduce quickly whether, for each group of digits, that group is going to propagate a carry that comes in from the right.
- 4. CLA -Continued Carry lookahead logic uses the concepts of generating and propagating carries. Although in the context of a carry lookahead adder, it is most natural to think of generating and propagating in the context of binary addition, the concepts can be used more generally than this For each bit in a binary sequence to be added, the Carry Look Ahead Logic will determine whether that bit pair will generate a carry or propagate a carry. This allows the circuit to "pre-process" the two numbers being added to determine the carry ahead of time. Then, when the actual addition is performed
- 5. Objective - generate all incoming carries in parallel Feasible - carries depend only on xn-1,xn-2,...,x0 and yn- 1,yn-2,…,y0 - information available to all stages for calculating incoming carry and sum bit Requires large number of inputs to each stage of adder - impractical Number of inputs at each stage can be reduced - find out from inputs whether new carries will be generated and whether they will be propagated
- 6. Carry Propagation If xi=yi=1 - carry-out generated regardless of incoming carry - no additional information needed If xi,yi=10 or xi,yi=01 - incoming carry propagated If xi=yi=0 - no carry propagation Gi=xi yi - generated carry ; Pi=xi+yi - propagated carry ci+1= xi yi + ci (xi + yi) = Gi + ci Pi Substituting ci=Gi-1+ci-1Pi-1 ci+1=Gi+Gi-1Pi+ci-1Pi-1Pi Further substitutions - All carries can be calculated in parallel from xn-1,xn-2,...,x0 , yn-1,yn-2,…,y0 , and forced carry c0
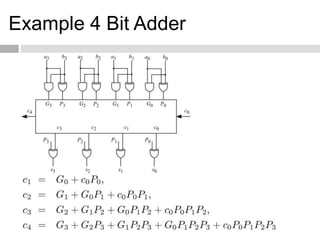
- 7. Example 4 Bit Adder
- 8. Delay of Carry-Look-Ahead Adders G - delay of a single gate At each stage Delay of G for generating all Pi and Gi Delay of 2G for generating all ci (two-level gate implementation) Delay of 2G for generating sum digits si in parallel (two- level gate implementation) Total delay of 5G regardless of n - number of bits in each operand Large n (=32) - large number of gates with large fan-in Fan-in - number of gate inputs, n+1 here Span of look-ahead must be reduced at expense of speed
- 9. Reducing Span n stages divided into groups - separate carry-look-ahead in each group Groups interconnected by ripple-carry method Equal-sized groups - modularity - one circuit designed Commonly - group size 4 selected - n/4 groups 4 is factor of most word sizes Technology-dependent constraints (number of input/output pins) ICs adding two 4 digits sequences with carry-look-ahead exist G needed to generate all Pi and Gi 2G needed to propagate a carry through a group once the Pi,Gi,c0 are available (n/4)2G needed to propagate carry through all groups 2G needed to generate sum outputs Total - (2(n/4)+3)G = ((n/2)+3)G - a reduction of almost 75% compared to 2nG in a ripple-carry adder
- 10. Further Addition Speed-Up Carry-look-ahead over groups Group-generated carry - G*=1 if a carry-out (of group) is generated internally Group-propagated carry - P*=1 if a carry-in (to group) is propagated internally to produce a carry-out (of group) For a group of size 4: Group-carries for several groups used to generate group carry-ins similarly to single-bit carry-ins A combinatorial circuit implementing these equations available - carry-look-ahead generator
- 11. 16-bit 2-level Carry-look-ahead Adder
- 12. n=16 - 4 groups Outputs G*0,G*1,G*2,G*3,P*0,P*1,P*2,P*3 Inputs to a carry-look-ahead generator with outputs c4,c8,c12
- 13. Operation - 4 steps: 1. All groups generate in parallel Gi and Pi - delay G 2. All groups generate in parallel group-carry-generate - G*i and group-carry-propagate - P*i - delay 2G 3. Carry-look-ahead generator produces carries c4,c8,c12 into the groups - delay 2G 4. Groups calculate in parallel individual sum bits with internal carry-look-ahead - delay 4G Total time - 9G If external carry-look-ahead generator not used and carry ripples among the groups - 11G Theoretical estimates only - delay may be different in practice Operation
- 14. Additional Levels of Carry-look-ahead Carry-look-ahead generator produces G** and P**, - section- carry generate and propagate section is a set of 4 groups and consists of 16 bits For 64 bits, either use 4 circuits with a ripple-carry between adjacent sections, or use another level of carry-look-ahead for faster execution This circuit accepts 4 pairs of section-carry-generate and section-carry-propagate, and produces carries c16, c32, and c48 As n increases, more levels of carry-look-ahead generators can be added Number of levels (for max speed up) logbn b is the blocking factor - number of bits in a group, number of groups in a section, and so on
- 15. Advantage & Disadvantage Advantage: Reduced Propagation Time(Delay) Fastest Addition logic Disadvantage: CLA is that the carry logic block gets very complicated for more than 4 -bits (CLAs are usually implemented as 4-bit modules and are used in a hierarchical structure to realize adders that have multiples of 4-bits)
- 16. References 1. Kamran Eshraghian, Douglas A Pucknell, and Sholeh Eshraghian, “Essentials of VLSI Circuits and Systems”, Prentice Hall of India, New Delhi, 2005. 2. Morris Mano, and M.D. Ciletti, “Digital Design ", Pearson Education, New Delhi, 2008. 3.John. F. Wakerly, “Digital design principles and practices”, Pearson Education, FourthEdition, 2007 . 4.Tokheim R L, “Digital Electronics - Principles and Applications ", Tata McGraw Hill, New Delhi, 2007. 5. Alan B Marcovitz, “Introduction to Logic Design”, second edition, Tata McGraw-Hill, New Delhi, 2005. 6. Neil H E Weste and Kamran Eshranghian, “Principles of CMOS VLSI Design: A system Perspective”, Addison Wesley, New Delhi, 2009.