Chapter 7 Regularization for deep learning - 2
- 1. 7.6 semi-supervised learning 목적 및 동기 강아지를 인식하는 모델을 만들고자 한다. 그런데 가지고 있는 데이터에 조금 문제가 있다. label이 된 데이터 label이 안 된 데이터 Label된 데이터로만 모델을 만들자니 데이터가 너무 적고, Label 안된 데이터에 labeling을 하자니 시간과 비용이 엄청나게 든다 어쩌지?
- 2. 7.6 semi-supervised learning Labeled data Labeled+unlabeled data 지도학습 준지도학습
- 3. 7.6 semi-supervised learning Labeled 데이터로만 분포를 추정하고 Decision boundary를 형성 불안정함 Labeled+unlabeled 데이터로 분포를 추정하고 Decision boundary를 형성 안정적인 분포
- 4. 7.7 multi-task learning 이것은 고양이인가요? ( O / X)
- 5. 7.7 multi-task learning 이것은 고양이인가요? ( O / X)
- 6. 7.7 multi-task learning 이것은 강아지인가요? ( O / X)
- 7. 7.7 multi-task learning 이것은 강아지인가요? ( O / X)
- 8. 7.7 multi-task learning 이것은 금색인가요? ( O / X)
- 9. 7.7 multi-task learning 이것은 금색인가요? ( O / X)
- 10. 7.7 multi-task learning feature 고양이임? ㄴㄴ 강아지임? ㅇㅇ 금색임? ㅇㅇ 금색 강아지구나!
- 11. 7.7 multi-task learning 고양이가 아니다. 강아지가 맞다. 금색이 맞다. 사실 우리는 거의 동시에(simultaneously) 위 세가지 문제를 해결합니다
- 12. 7.7 multi-task learning feature 고양이임? ㄴㄴ -> 0 강아지임? ㅇㅇ -> 1 금색임? ㅇㅇ -> 1 금색 강아지구나!
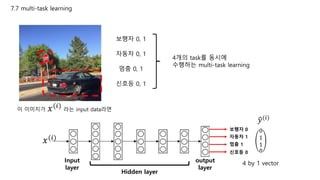
- 13. 7.7 multi-task learning 보행자 0, 1 자동차 0, 1 멈춤 0, 1 신호등 0, 1 4개의 task를 동시에 수행하는 multi-task learning 이 이미지가 𝑥(𝑖) 라는 input data라면 보행자 0 자동차 1 멈춤 1 신호등 0 𝑦(𝑖) 0 1 1 0 4 by 1 vectorInput layer output layer Hidden layer 𝑥(𝑖)
- 14. 7.7 multi-task learning Cost 계산 𝑦(𝑖) 1 0 1 0 만약 이라면𝑦(𝑖) 0 1 1 0 𝐶𝑜𝑠𝑡 = 𝐶𝑜𝑠𝑡 1,0 + 𝐶𝑜𝑠𝑡 0,1 + 𝐶𝑜𝑠𝑡 1,1 + 𝐶𝑜𝑠𝑡 0,0 4 이때 Cost function은 대부분 log loss 𝑦1 (𝑖) 𝑦2 (𝑖) 𝑦3 (𝑖) 𝑦4 (𝑖) 각 성분은 𝑦𝑗 (𝑖) 로 표현 1 𝑛 𝑖 𝑛 𝑗 𝑚 𝐶𝑜𝑠𝑡( 𝑦𝑗 (𝑖) , 𝑦𝑗 (𝑖) ) n = example 수 m = task 수일반화 하면 보행자 0 자동차 1 멈춤 1 신호등 0 𝑦(𝑖) 0 1 1 0 Input layer output layer Hidden layer 𝑥(𝑖)
- 15. 7.7 multi-task learning 다른 이미지 데이터 𝑦(𝑖) 보행자 NA 자동차 0 멈춤 1 신호등 NA 이미지 데이터에 labeling이 안되어 있는 경우 Cost 계산 𝑦(𝑖) 1 1 1 0 𝑦(𝑖) 𝑁𝐴 0 1 𝑁𝐴 𝐶𝑜𝑠𝑡 𝑠𝑢𝑚 = 𝐶𝑜𝑠𝑡 1, 𝑁𝐴 + 𝐶𝑜𝑠𝑡 1,0 + 𝐶𝑜𝑠𝑡 1,1 + 𝐶𝑜𝑠𝑡 0, 𝑁𝐴 4 𝑦1 (𝑖) 𝑦2 (𝑖) 𝑦3 (𝑖) 𝑦4 (𝑖) 1 𝑛 𝑖 𝑛 𝑗 𝑚 𝐶𝑜𝑠𝑡( 𝑦𝑗 (𝑖) , 𝑦𝑗 (𝑖) ) n = example 수 m = task 수𝑦𝑗 (𝑖) 가 NA인것 제외하고 요 두 개는 제외하고 계산
- 16. 7.7 multi-task learning 아키텍처를 좀 더 뜯어보면 1. 모든 task가 공유하는 일반적인 파라미터를 학습하는 부분 2. Task에 고유한 파라미터를 학습하는 부분
- 17. 7.7 multi-task learning Multi-task learning이 regularization 방법인 이유 경욱 연준 경욱의 특징 : 아무리 심한 말을 해도 다 받아줌 다빈 연준 다빈의 특징 : 심한 말을 하면 극대노함 각 task 마다 noise 패턴이 다름. 여러 noise 패턴을 동시에 학습을 하려다 보니 general한 모델 탄생 연준의 성격 : 심한 말을 많이 하는 성격이 됨. 다빈과는 친구가 될 수 없음 ㅠㅠ 연준경욱 다빈 두 명의 특징을 다 받아들여 일반적인 성격을 가지게 됨
- 18. 7.7 multi-task learning 언제 multi-task learning을 쓸 수 있나요? 1. 각각의 task가 서로의 task에 도움이 되는 비슷한 특성을 가질 때. 2. 각 task에 대해 큰 신경망을 훈련할 수 있어야 함. 큰 신경망의 경우 task를 각각 하는 것 보다 성능이 좋은 경우가 거의 대다수 **Rich Caruana라는 연구자가 밝혀낸 내용. 그리고 multi-task learning은 다른 분야에서는 많이 쓰이지 않지만 computer vision 분야에서는 많이 쓰인다.
- 19. 7.8 Early stopping Epoch ↑ training set에 Overfitting Generalization error ↑ 그래서 적당한 시점에 끊어야 함
- 20. 7.8 Early stopping 갓경욱님께 감사를… Input Hidden Layer1 Hidden Layer2 Output Layer x1 x2 w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 b1 b3 b5 b2 b4 빠른 진행을 위해 수치에 대한 계산은 배제하겠습니다. Training Set 𝑥(1) 𝑥(2) 𝑥(3) 𝑥(𝑛) … 𝑦(1)
- 21. 7.8 Early stopping Input Hidden Layer1 Hidden Layer2 Output Layer x1 x2 w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 b1 b3 b5 b2 b4 Training Set 𝑥(1) 𝑥(2) 𝑥(3) 𝑥(𝑛) … 𝑦(1) FeedForward propagation
- 22. 7.8 Early stopping Input Hidden Layer1 Hidden Layer2 Output Layer x1 x2 w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 b1 b3 b5 b2 b4 Training Set 𝑥(1) 𝑥(2) 𝑥(3) 𝑥(𝑛) … 𝑦(1)
- 23. 7.8 Early stopping Input Hidden Layer1 Hidden Layer2 Output Layer x1 x2 w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 b1 b3 b5 b2 b4 Training Set 𝑥(1) 𝑥(2) 𝑥(3) 𝑥(𝑛) … 𝑦(1)
- 24. 7.8 Early stopping Input Hidden Layer1 Hidden Layer2 Output Layer x1 x2 w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 b1 b3 b5 b2 b4 Training Set 𝑥(1) 𝑥(2) 𝑥(3) 𝑥(𝑛) … 𝑦(1)
- 25. 7.8 Early stopping Input Hidden Layer1 Hidden Layer2 Output Layer x1 x2 w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 b1 b3 b5 b2 b4 Training Set 𝑥(1) 𝑥(2) 𝑥(3) 𝑥(𝑛) … 𝑦(1)
- 26. 7.8 Early stopping Input Hidden Layer1 Hidden Layer2 Output Layer x1 x2 w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 b1 b3 b5 b2 b4 Training Set 𝑥(1) 𝑥(2) 𝑥(3) 𝑥(𝑛) … 𝑦(1) 𝑦(1)
- 27. 7.8 Early stopping Input Hidden Layer1 Hidden Layer2 Output Layer x1 x2 w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 b1 b3 b5 b2 b4 Training Set 𝑥(1) 𝑥(2) 𝑥(3) 𝑥(𝑛) … 𝒙(𝟐) ~𝒙(𝒏) 까지 반복 𝑦(2)
- 28. 7.8 Early stopping Training Set 𝑥(1) 𝑥(2) 𝑥(3) 𝑥(𝑛) … 𝒊 𝑦(𝑖) 𝑦(𝑖) 1 0.7 0.99 2 0.6 1.55 3 0.2 1.4 4 0.4 0.3 … … … n 𝑦(𝑛) 𝑦(𝑛) 𝐶𝑜𝑠𝑡 𝑠𝑢𝑚 = 𝐶𝑜𝑠𝑡 0.7,0.99 + 𝐶𝑜𝑠𝑡 0.6,1.55 + ⋯ + 𝐶𝑜𝑠𝑡 𝑦(𝑛), 𝑦(𝑛) 𝑛 = 1 𝑛 𝑖 𝑛 𝐶𝑜𝑠𝑡( 𝑦(𝑖) , 𝑦(𝑖) ) Feed forward outputinput Cost 함수 계산
- 29. 7.8 Early stopping 𝐶𝑜𝑠𝑡 𝑠𝑢𝑚 = 𝐶𝑜𝑠𝑡 0.7,0.99 + 𝐶𝑜𝑠𝑡 0.6,1.55 + ⋯ + 𝐶𝑜𝑠𝑡 𝑦(𝑛) , 𝑦(𝑛) 𝑛 = 1 𝑛 𝑖 𝑛 𝐶𝑜𝑠𝑡( 𝑦(𝑖) , 𝑦(𝑖) ) Cost sum 을 최소로 하는 𝑤, 𝑏 를 구해 updating 1 iteration = 1 epoch
- 30. 7.8 Early stopping Training Set Validation Set Test Set Training Set 데이터셋 정의 Model Validation Set Epoch(𝒊) 0 Parameter(w,b=𝜽) 𝜽 𝟎 Validation error(𝝊) 𝝊 𝟎 랜덤 초기값 ∞로 set 𝜽∗ = 𝜽 𝟎, 𝒊∗ =0 현재까지 𝝊 𝟎가 가장 낮은 값 𝝊 = 𝝊 𝟎 𝝊에 해당하는 파라미터 𝜽 𝟎, 𝒊 𝜽∗ , 𝒊∗ 는 최적의 파라미터와 최적의 epoch
- 31. 7.8 Early stopping Training Set Validation Set Test Set Training Set 데이터셋 정의 Model Validation Set Epoch(𝒊) 0 Parameter(w,b=𝜽) 𝜽 𝟎 Validation error(𝝊) 𝝊 𝟎 𝜽∗ = 𝜽 𝟏, 𝒊∗ = 𝟏 현재까지 𝝊 𝟏가 가장 낮은 값 𝝊 = 𝝊 𝟏 𝝊에 해당하는 파라미터 𝜽 𝟏, 𝒊 1 𝜽 𝟏 𝝊 𝟏 If 𝝊 𝟏 < 𝝊
- 32. 7.8 Early stopping Training Set Validation Set Test Set Training Set 데이터셋 정의 Model Validation Set Epoch(𝒊) 0 Parameter(w,b=𝜽) 𝜽 𝟎 Validation error(𝝊) 𝝊 𝟎 𝜽∗ = 𝜽 𝟐, 𝒊∗ = 𝟐 현재까지 𝝊 𝟐가 가장 낮은 값 𝝊 = 𝝊 𝟐 𝝊에 해당하는 파라미터 𝜽 𝟐, 𝒊 1 𝜽 𝟏 𝝊 𝟏 If 𝝊 𝟐 < 𝝊 2 𝜽 𝟐 𝝊 𝟐
- 33. 7.8 Early stopping Training Set Validation Set Test Set Training Set 데이터셋 정의 Model Validation Set Epoch(𝒊) 0 Parameter(w,b=𝜽) 𝜽 𝟎 Validation error(𝝊) 𝝊 𝟎 1 𝜽 𝟏 𝝊 𝟏 If 𝝊 𝟏𝟎𝟎 > 𝝊 2 𝜽 𝟐 𝝊 𝟐 100 𝜽 𝟏𝟎𝟎 𝝊 𝟏𝟎𝟎 … … … 현재 𝝊=𝝊 𝟗𝟗 𝜽∗ = 𝜽 𝟗𝟗 𝒊∗ = 𝟗𝟗 바로 stop??? 너무 정이 없으니 몇 번 봐주기로 합시다! 몇 번 = p이라고 표현(patience)
- 34. 7.8 Early stopping Training Set Validation Set Test Set Training Set 데이터셋 정의 Model Validation Set Epoch(𝒊) 0 Parameter(w,b=𝜽) 𝜽 𝟎 Validation error(𝝊) 𝝊 𝟎 𝜽∗ = 𝜽 𝟗𝟗, 𝒊∗ = 𝟗𝟗 현재까지 𝝊 𝟗𝟗가 가장 낮은 값 𝝊 = 𝝊 𝟗𝟗 𝝊에 해당하는 파라미터 𝜽 𝟗𝟗, 𝒊 1 𝜽 𝟏 𝝊 𝟏 If 𝝊 𝟏𝟎𝟎 > 𝝊 2 𝜽 𝟐 𝝊 𝟐 100 𝜽 𝟏𝟎𝟎 𝝊 𝟏𝟎𝟎 … … … p=2 이므로 다음 epoch으로 넘어감 p=2
- 35. 7.8 Early stopping Training Set Validation Set Test Set Training Set 데이터셋 정의 Model Validation Set Epoch(𝒊) 0 Parameter(w,b=𝜽) 𝜽 𝟎 Validation error(𝝊) 𝝊 𝟎 𝜽∗ = 𝜽 𝟗𝟗, 𝒊∗ = 𝟗𝟗 현재까지 𝝊 𝟗𝟗가 가장 낮은 값 𝝊 = 𝝊 𝟗𝟗 𝝊에 해당하는 파라미터 𝜽 𝟗𝟗, 𝒊 1 𝜽 𝟏 𝝊 𝟏 If 𝝊 𝟏𝟎𝟏 > 𝝊 2 𝜽 𝟐 𝝊 𝟐 100 𝜽 𝟏𝟎𝟎 𝝊 𝟏𝟎𝟎 … … … 다음 epoch으로 넘어감 p=2-1 101 𝜽 𝟏𝟎𝟏 𝝊 𝟏𝟎𝟏
- 36. 7.8 Early stopping Training Set Validation Set Test Set Training Set 데이터셋 정의 Model Validation Set Epoch(𝒊) 0 Parameter(w,b=𝜽) 𝜽 𝟎 Validation error(𝝊) 𝝊 𝟎 𝜽∗ = 𝜽 𝟗𝟗, 𝒊∗ = 𝟗𝟗 현재까지 𝝊 𝟗𝟗가 가장 낮은 값 𝝊 = 𝝊 𝟗𝟗 𝝊에 해당하는 파라미터 𝜽 𝟗𝟗, 𝒊 1 𝜽 𝟏 𝝊 𝟏 If 𝝊 𝟏𝟎𝟐 > 𝝊 2 𝜽 𝟐 𝝊 𝟐 100 𝜽 𝟏𝟎𝟎 𝝊 𝟏𝟎𝟎 … … … 이제 진짜 STOP! p=2-2 101 𝜽 𝟏𝟎𝟏 𝝊 𝟏𝟎𝟏 102 𝜽 𝟏𝟎𝟐 𝝊 𝟏𝟎𝟐
- 37. 7.8 Early stopping Model Epoch(iteration) 99 Parameter(w,b=𝜽) 𝜽 𝟗𝟗 optimal Training Set Validation Set Test Set Training Set Test Set 방법1 𝜽 𝟗𝟗 를 그대로 이용 훈련 1 MSE > 훈련 2 MSE 이면 epoch 종료 훈련 1 훈련 2 방법2 Epoch = 99 를 이용해서 훈련 no.2 진행 단점 : 종료가 안 될 수도…
- 38. 7.8 Early stopping Early stopping과 L2 regularization의 관련성
- 39. 7.8 Early stopping 왜 regularization이 overfitting을 줄일 까요? 𝑎 = 𝑔 𝑤𝑥 + 𝑏 = 𝑔 𝑧 = 𝑦 𝑔 𝑥 ∶ 𝑎𝑐𝑡𝑖𝑣𝑎𝑡𝑖𝑜𝑛 함수 sigmoid tanh 𝑔 𝑧 에서 𝑧가 0에 가까워 질수록 선형에 근사 모델이 더 간단해짐 𝐽 𝑤 = 𝐽 𝑤 + 𝛼 2 𝑤 𝑇 𝑤 𝛼 ↑ 면 𝑤 𝑇 𝑤 ↓ 니까 𝑤 ↓
- 40. 7.8 Early stopping “난 Early stopping 잘 안 씀” “L2 짱"
- 41. 7.9 Parameter Tying and Parameter sharing CNN(Convolutional Neural Network)의 기반이 되는 개념 기본 가정 𝑤(𝐴) 𝑤(𝐵) 모델A 모델B 같은 task를 수행하는 두 모델(둘 다 고양이를 식별하는 모델) 일 때 같은 task를 수행하기 때문에 input과 output의 분포가 비슷하고 𝑤(𝐴) 와 𝑤(𝐵) 도 가까울 것 or 동일할 것이다.
- 42. 7.9 Parameter Tying and Parameter sharing 저렇게 이미지를 여러 단위로 나누어도 나눠진 이미지 마다 다른 파라미터가 매겨지는 것이 아니라 같은 파라미터를 공유하는 것.
- 43. 7.10 Sparse representation(희소표현) L1 regularization 에서는 L2와 달리 w가 0으로 수렴하는 특징이 있었다. input output InputOutput W 행렬 0 많음 = 희소함 이것을 매개변수(parameter) 희소성이라고 함 …. ….
- 44. 7.10 Sparse representation(희소표현) Activation function g(z) 에 L1 regularization을 적용하면 input output …. …. inputW 행렬output Activation function을 거친 input을 희소하게 만든다. 요것이 표현(representation) 희소성 무슨 의미냐 하면
- 45. 7.10 Sparse representation(희소표현) 𝑧(𝐿−1) = 𝑤(𝐿−1) 𝑥 + 𝑏(𝐿−1) 𝑔 𝑥 ∶ 𝑎𝑐𝑡𝑖𝑣𝑎𝑡𝑖𝑜𝑛 함수 L-2 L-1 L 𝑎(𝐿−1) = 𝑔(𝑧 𝐿−1 ) 𝑧(𝐿) = 𝑤(𝐿) 𝑎(𝐿−1) + 𝑏(𝐿) 𝑎(𝐿) = 𝑔(𝑧 𝐿 ) 𝑎(𝐿−1) = 𝑔 𝑤(𝐿−1) 𝑎(𝐿−2) + 𝑏(𝐿−1) sigmoid tanh 얘가 희소해짐
- 46. 7.10 Sparse representation(희소표현) L1 regularization 적용하는 것 말고 또 있음 0이 되는 부분 존재