Comparing Metaheuristic Algorithms for Error Detection in Java Programs
- 1. Conclusions Introduction Background Algorithms Experiments & Future Work Comparing Metaheuristic Algorithms for Error Detection in Java Programs Francisco Chicano, Marco Ferreira and Enrique Alba SSBSE 2011, Szeged, Hungary, September 10-12 1 / 25
- 2. Conclusions Introduction Background Algorithms Experiments & Future Work Motivation Motivation • Concurrent software is difficult to test ... • ... and it is in the heart of a lot of critical systems • Techniques for proving the correctness of concurrent software are required • Model checking → fully automatic • Traditional techniques for this purpose have problems with large models • We compare several metaheuristics and classical algorithms for model checking SSBSE 2011, Szeged, Hungary, September 10-12 2 / 25
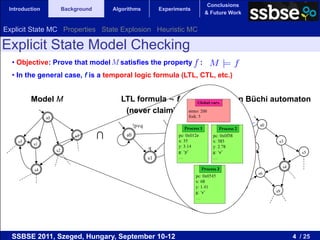
- 3. Conclusions Introduction Background Algorithms Experiments & Future Work Explicit State MC Properties State Explosion Heuristic MC Explicit State Model Checking • Objective: Prove that model M satisfies the property : • In the general case, f is a temporal logic formula (LTL, CTL, etc.) Model M LTL formula ¬ f Intersection Büchi automaton (never claim) s0 !p∨q s0 s5 s3 ∩ s0 s2 s1 s3 s1 p∧!q s2 q s2 s5 s1 s7 s4 s4 s6 s8 s9 SSBSE 2011, Szeged, Hungary, September 10-12 3 / 25
- 4. Conclusions Introduction Background Algorithms Experiments & Future Work Explicit State MC Properties State Explosion Heuristic MC Explicit State Model Checking • Objective: Prove that model M satisfies the property : • In the general case, f is a temporal logic formula (LTL, CTL, etc.) Model M LTL formula ¬ f Intersection Büchi automaton (never claim) s0 !p∨q s0 s5 s3 ∩ s0 s2 = s1 s3 s1 p∧!q s2 q s2 s5 s1 s7 s4 s4 s6 s8 s9 SSBSE 2011, Szeged, Hungary, September 10-12 4 / 25
- 5. Conclusions Introduction Background Algorithms Experiments & Future Work Explicit State MC Properties State Explosion Heuristic MC Explicit State Model Checking • Objective: Prove that model M satisfies the property : • In the general case, f is a temporal logic formula (LTL, CTL, etc.) Model M LTL formula ¬ f Intersection Büchi automaton (never claim) s0 !p∨q s0 s5 s3 ∩ s0 s2 = s1 s3 s1 p∧!q s2 q s2 s5 s1 s7 s4 s4 s6 s8 s9 Using Nested-DFS SSBSE 2011, Szeged, Hungary, September 10-12 5 / 25
- 6. Conclusions Introduction Background Algorithms Experiments & Future Work Explicit State MC Properties State Explosion Heuristic MC Safety properties s0 s1 s3 Properties in s2 s5 JPF s7 s4 • Exceptions s6 • Deadlocks s8 s9 • An error trail is an execution path ending in an error state • The search for errors is transformed in a graph exploration problem (DFS, BFS) SSBSE 2011, Szeged, Hungary, September 10-12 6 / 25
- 7. Conclusions Introduction Background Algorithms Experiments & Future Work Explicit State MC Properties State Explosion Heuristic MC State Explosion Problem • Number of states very large even for small models s0 s1 s3 s2 Memory s5 s7 s4 s6 s8 s9 • Example: Dining philosophers with n philosophers → 3n states • For each state we need to store the heap and the stacks of the different threads • Solutions: collapse compression, minimized automaton representation, bitstate hashing, partial order reduction, symmetry reduction • Large models cannot be verified but errors can be found SSBSE 2011, Szeged, Hungary, September 10-12 7 / 25
- 8. Conclusions Introduction Background Algorithms Experiments & Future Work Explicit State MC Properties State Explosion Heuristic MC Heuristic Model Checking • The search for errors can be directed by using heuristic information 5 s0 2 2 Heuristic value s1 3 s3 s2 1 s5 0 s7 4 s4 0 s6 6 s8 7 s9 • Different kinds of heuristic functions have been proposed in the past: • Formula-based heuristics • Deadlock-detection heuristics • Structural heuristics • State-dependent heuristics SSBSE 2011, Szeged, Hungary, September 10-12 8 / 25
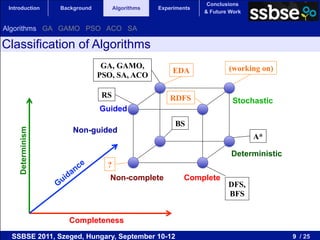
- 9. Conclusions Introduction Background Algorithms Experiments & Future Work Algorithms GA GAMO PSO ACO SA Classification of Algorithms GA, GAMO, (working on) EDA PSO, SA, ACO RS RDFS Stochastic Guided BS Non-guided Determinism A* Deterministic ? Non-complete Complete DFS, BFS Completeness SSBSE 2011, Szeged, Hungary, September 10-12 9 / 25
- 10. Conclusions Introduction Background Algorithms Experiments & Future Work Algorithms GA GAMO PSO ACO SA Genetic Algorithm Solution encoding (floating point values) 0.5 0.1 0.9 0.3 0.5 0.9 Crossover Mutation 0.5 0.1 0.9 0.3 0.5 0.9 → 0.5 0.1 0.6 0.3 0.5 0.9 SSBSE 2011, Szeged, Hungary, September 10-12 10 / 25
- 11. Conclusions Introduction Background Algorithms Experiments & Future Work Algorithms GA GAMO PSO ACO SA Genetic Algorithm with Memory Operator Solution encoding (floating point values) 0.5 0.1 0.9 0.3 0.5 0.9 Index in a table of states 0 1 2 3 … … SSBSE 2011, Szeged, Hungary, September 10-12 11 / 25
- 12. Conclusions Introduction Background Algorithms Experiments & Future Work Algorithms GA GAMO PSO ACO SA Particle Swarm Optimization Particles 0.2 -1.4 -3.5 → Position (solution) 1.0 10.3 7.2 → Velocity Personal best Inertia Global best SSBSE 2011, Szeged, Hungary, September 10-12 12 / 25
- 13. Conclusions Introduction Background Algorithms Experiments & Future Work Algorithms GA GAMO PSO ACO SA Ant Colony Optimization Trail k τij • The ant selects stochastically its next node Heuristic i ηij Ni • The probability of selecting one node depends on the pheromone trail and the m heuristic value (optional) of the edge/node j l • The ant stops when a complete k solution is built SSBSE 2011, Szeged, Hungary, September 10-12 13 / 25
- 14. Conclusions Introduction Background Algorithms Experiments & Future Work Algorithms GA GAMO PSO ACO SA Simulated Annealing Neighbor 0.5 0.1 0.9 0.3 0.5 0.9 → 0.5 0.1 0.6 0.3 0.5 0.9 SSBSE 2011, Szeged, Hungary, September 10-12 14 / 25
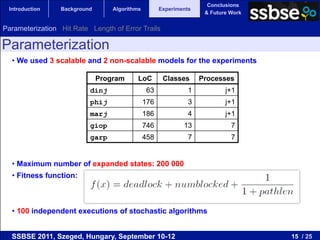
- 15. Conclusions Introduction Background Algorithms Experiments & Future Work Parameterization Hit Rate Length of Error Trails Parameterization • We used 3 scalable and 2 non-scalable models for the experiments Program LoC Classes Processes dinj 63 1 j+1 phij 176 3 j+1 marj 186 4 j+1 giop 746 13 7 garp 458 7 7 • Maximum number of expanded states: 200 000 • Fitness function: • 100 independent executions of stochastic algorithms SSBSE 2011, Szeged, Hungary, September 10-12 15 / 25
- 16. Conclusions Introduction Background Algorithms Experiments & Future Work Parameterization Hit Rate Length of Error Trails Parameterization • We used 3 scalable and 2 non-scalable models for the experiments Program LoC Classes Processes j=4 to 20 dinj 63 1 j+1 phij 176 to 36 3 j=4 j+1 marj 186 4 j+1 giop 746j=2 to 1013 7 garp 458 7 7 • Maximum number of expanded states: 200 000 • Fitness function: • 100 independent executions of stochastic algorithms SSBSE 2011, Szeged, Hungary, September 10-12 16 / 25
- 17. Conclusions Introduction Background Algorithms Experiments & Future Work Parameterization Hit Rate Length of Error Trails Hit rate SSBSE 2011, Szeged, Hungary, September 10-12 17 / 25
- 18. Conclusions Introduction Background Algorithms Experiments & Future Work Parameterization Hit Rate Length of Error Trails Hit rate phi SSBSE 2011, Szeged, Hungary, September 10-12 18 / 25
- 19. Conclusions Introduction Background Algorithms Experiments & Future Work Parameterization Hit Rate Length of Error Trails Hit rate din SSBSE 2011, Szeged, Hungary, September 10-12 19 / 25
- 20. Conclusions Introduction Background Algorithms Experiments & Future Work Parameterization Hit Rate Length of Error Trails Hit rate SSBSE 2011, Szeged, Hungary, September 10-12 20 / 25
- 21. Conclusions Introduction Background Algorithms Experiments & Future Work Parameterization Hit Rate Length of Error Trails Length of Error Trails BS: 753 SSBSE 2011, Szeged, Hungary, September 10-12 21 / 25
- 22. Conclusions Introduction Background Algorithms Experiments & Future Work Parameterization Hit Rate Length of Error Trails Length of Error Trails BS: 172 DFS: 245 BS: 260 DFS: 378 SSBSE 2011, Szeged, Hungary, September 10-12 22 / 25
- 23. Conclusions Introduction Background Algorithms Experiments & Future Work Parameterization Hit Rate Length of Error Trails Length of Error Trails SSBSE 2011, Szeged, Hungary, September 10-12 23 / 25
- 24. Conclusions Introduction Background Algorithms Experiments & Future Work Conclusions & Future Work Conclusions & Future Work Conclusions • Metaheuristics are more effective than classical algorithms in finding errors • Beam Search has advantages over complete search algorithms • An even distribution of the search in depth levels tends to raise hit rate • Stochastic algorithms obtain short error trails Future Work • Design a stochastic complete guided algorithm to find errors and verify • Design of hybrid algorithms to more efficiently explore the search space • Explore the design of parallel metaheuristics for this problem SSBSE 2011, Szeged, Hungary, September 10-12 24 / 25
- 25. Comparing Metaheuristic Algorithms for Error Detection in Java Programs Thanks for your attention !!! SSBSE 2011, Szeged, Hungary, September 10-12 25 / 25