Data structure algorithm

DEPARTMENT OF COMPUTER SCIENCE &
INFORMATION TECHOLOGY
V.S PRIYADHARSHINI
I.MSC(CS)

DATA STRUCTURES AND ALGORITHMS
TOPIC: SUM OF SUBSET ,GRAPH COLORS

SUM OF SUBSET
Subset Sum Problem:
It is one of the most important problems in complexity
theory. The problem is given an A set of integers a1,
a2,…., an upto n integers. The question arises that is
there a non-empty subset such that the sum of the
subset is given as M integer?. For example, the set is
given as [5, 2, 1, 3, 9], and the sum of the subset is 9;
the answer is YES as the sum of the subset [5, 3, 1] is
equal to 9. This is an NP-complete problem again. It is
the special case of knapsack

SUM OF SUBSET
Let's understand this problem through an example:
 problem.
 We have a set of 5 integers given below:
N = 4, -2, 2, 3, 1
 We want to find out the subset whose sum is equal to 5. There
are many solutions to this problem.
 The naïve approach, i.e., brute-force search generates all the
possible subsets of the original array, i.e., there are 2n possible
states. Here the running time complexity would be exponential.
Then, we consider all these subsets in O(N) linear running time
and checks whether the sum of the items is M or not.
 The dynamic programming has pseudo-polynomial running
time.

SUM OF SUBSET
Statement: Given a set of positive integers, and a value sum, determine that the
sum of the subset of a given set is equal to the given sum.
Or
Given an array of integers and a sum, the task is to have all subsets of given
array with sum equal to the given sum.
Example 1:
Input: set[] = {4, 16, 5, 23, 12}, sum = 9
Output = true
Subset {4, 5} has the sum equal to 9.
Example 2:
Input: set[] = {2, 3, 5, 6, 8, 10}, sum = 10
Output = true
There are three possible subsets that have the sum equal to 10.
Subset1: {5, 2, 3}
Subset2: {2, 8}
Subset3: {10}

SUM OF SUBSET
There are two ways of solving the subset problem:
 Recursion
 Dynamic programming
Method 1: Recursion
 Before knowing about the recursive approach, we should know about two
things in a subset which are given below:
 Include: Here include means that we are selecting the element from the array.
 Exclude: Here, exclude means that we are rejecting the element from the array.
To implement the recursive approach, we consider the following two cases:
 Now we consider the first element and now the required sum is equal to the
difference between the target sum and value of first element. The number of
elements is equal to the difference between the total elements and 1.
 Leave the 'first' element and now the required sum = target sum. The number
of elements is equal to the difference between the total elements and 1.

Let's understand that how can we solve the problem
using recursion. Consider the array which is given
below:
arr = [3, 4, 5, 2]
sum = 9
result = []
In the above example, we have taken an array, and the
empty array named result that stores all the values
whose resultant sum is equal to 9.

First element in an array is 3. There are two
scenarios:
First scenario is select. The sum is equal to the target
sum - value of first element, i.e., 9 - 3 = 6 and the
first element, i.e., 3 gets stored in the result array, i.e.,
result[].
Second scenario is reject. The array arr contains the
elements 4, 5, 2, i.e., arr = [4, 5, 2] and sum would be
same as 9 as we are rejecting the element 3. The
result[] array would remain empty.

Now we perform the same select and reject operation
on element 4 as it is the first element of the array now.
Select the element 4 from the array. Since we are selecting 4
from the array so array arr would contain the elements 5, 2,
i.e., arr = [5, 2]. The sum is equal to the 6-4 = 2 and the
element 4 gets stored in the result arr. The result[] = {3, 4}.
Reject the element 4 from the array. Since we are rejecting
the 4 from the array so array arr would contain the
elements 5, 2, i.e., arr = [5, 2]. The sum would remain same
as 6 and the result array would be same as previous, i.e., {3}.

Now we perform the select and reject operation on element 5.
Select the element 5 from the array. Since we are selecting 5 from the
array so array arr would contain the elements 2, i.e., arr = [2]. The sum
is equal to the 2 - 5 equals to -3 and the element 5 gets stored in the
result arr. The result[] = {3, 4, 5}. Reject the element 5 from the array.
Since we are rejecting 5 from the array so array arr would contain the
element 2, i.e., arr = [2]. The sum would remain same as previous, i.e., 6
and the result array would be same as previous, i.e., {3, 4}.

 If we observe S-5, we can see
that the sum is negative that
returns false. It means that there
is no further subset available in
the set.
Consider R-5. It also has two
scenarios:
 Select the element 2 from the
array. Once the element 2 gets
selected, the array becomes
empty, i.e., arr[] = " ". The sum
would be 2-2 equals to 0 and the
element 2 gets stored in the
result array. The result[] = [3, 4,
2].
 Reject the element 2 from the
array. Once the element 2 gets
rejected, the array becomes
empty, i.e., arr[] = " ". The sum
would be same as previous, i.e.,
2 and the result array would also
be same as previous, i.e., [3, 4].

Consider R-4. It has two
scenarios:
array. Since we are selecting 5
from the array so array arr
would contain the elements
2, i.e., arr = [2]. The sum
would be 6-5 equals to 1 and
the element 5 gets stored in
the result array. The result[] =
[3, 5].
array. Since we are rejecting 5
would contain the element 2,
i.e., arr = [2]. The sum would
remain same as previous, i.e.,
6 and the result array would
be same as previous, i.e., {3}.

Consider S-5. It has two
scenarios:
 Select the element 2 from
the array. Since we are
selecting 2 from the array
so array arr would be
empty, i.e., arr = " ". The
sum would be 1-2 equals to
-1 and the element 2 gets
stored in the result array.
The result[] = [3, 5, 2].
 Reject the element 2 from
the array. Since we are
rejecting 2 from the array
so array arr would become
empty. The sum would
remain same as previous,
i.e., 1 and the result array
would be same as previous,
i.e., {3, 5}.

Consider R-5. It has two
scenarios:
array. Since we are selecting 2
would be empty, i.e., arr = " ".
The sum would be 6-2 equals
to 4 and the element 2 gets
stored in the result array. The
result[] = [3, 2].
array. Since we are rejecting 2
would become empty. The
sum would remain same as
previous, i.e., 6 and the result
array would be same as
previous, i.e., {3}.

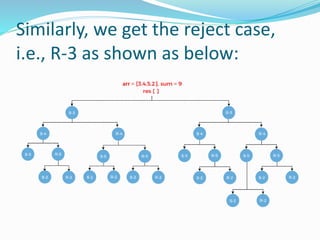
Similarly, we get the reject case,
i.e., R-3 as shown as below:

Graph coloring
Graph:
A graph is a unique data structure in programming that
consists of finite sets of nodes or vertices and a set of edges that
connect these vertices to them. At this moment, adjacent
vertices can be called those vertices that are connected to the
same edge with each other. In simple terms, a graph is a visual
representation of vertices and edges sharing some connection or
relationship. Although there are plenty of graph algorithms that
you might have been familiar with, only some of them are put to
use. The reason for this is simple as the standard graph
algorithms are designed in such a way to solve millions of
problems with just a few lines of logically coded technique. To
some extent, one perfect algorithm is solely optimized to achieve
such efficient results.

Graph coloring
Types of Graphs:
There are various types of graph algorithms that you would be looking
at in this article but before that, let's look at some types of terms to
imply the fundamental variations between them.
 Order: Order defines the total number of vertices present in the graph.
 Size: Size defines the number of edges present in the graph.
 Self-loop: It is the edges that are connected from a vertex to itself.
 Isolated vertex: It is the vertex that is not connected to any other
vertices in the graph.
 Vertex degree: It is defined as the number of edges incident to a vertex
in a graph.
 Weighted graph: A graph having value or weight of vertices.
 Unweighted graph: A graph having no value or weight of vertices.
 Directed graph: A graph having a direction indicator.
 Undirected graph: A graph where no directions are defined.

Graph coloring
Graph coloring:
Graph coloring algorithms follow the approach of
assigning colors to the elements present in the graph under
certain conditions. The conditions are based on the
techniques or algorithms. Hence, vertex coloring is a
commonly used coloring technique followed here. First, in
this method, you try to color the vertex using k color,
ensuring that two adjacent vertexes should not have the
same color. Other method includes face coloring and edge
coloring. Both of these methods should also ensure that no
edge or face should be inconsequent color. The coloring of
the graph is determined by knowing the chromatic
number, which is also the smaller number of colors
needed.

Data structure algorithm

More Related Content

What's hot (19)

Similar to Data structure algorithm (20)

More from PriyadharshiniVS (20)

Recently uploaded (20)

Data structure algorithm