DEsign of Flywheel new.ppt

• Necessity
In a combustion engine, & especially
in one with one or two cylinders, energy is
imparted to the crankshaft intermittently, & in
order to keep it rotating at a fairly uniform
speed under a substantially constant load, it is
necessary to provide it with a flywheel.
Flywheel

• In a single cylinder engine(4 Stroke), in which
there is only one power stroke in two
revolutions of the crankshaft, a considerable
fraction of energy generated per cycle is stored
in the flywheel, & the proportion thus stored
decreases with an increase in the No. of
cylinders
• In a 4 cylinder engine about 40% of the energy
of the cycle is temporarily stored.
Flywheel

However,
not all of this energy goes into flywheel
During the 1st half of the power stroke, when
energy is being supplied in excess by the burning
gases, all of the reciprocating parts of the engine
are being accelerated & absorb energy; besides, the
rotating parts other than the flywheel also have
some flywheel capacity, & this reduces the
proportion of the energy of the cycle which must be
stored in the flywheel.
Flywheel

• In a 6 cylinder engine the proportion of the energy
which must be absorbed & returned by the moving
parts amounts to about 20%.
• The greater the No. of cylinders the smaller the
flywheel capacity required per unit of piston
displacement, because the overlap of power
strokes is greater & besides other rotating parts of
the engine have greater inertia.
Flywheel

• However, the flywheel has by far the greatest
inertia even in a multi cylinder engine.
• Aside from its principle function, the fly wheel
serves as a member of the friction clutch, & it
usually carries also the ring gear of the electric
starter.
Flywheel

Flywheel
•Energy accumulator
•Energy re-distributor
•A flywheel serves as a reservoir which stores
energy during the period when the supply of
energy is more than the requirement &
releases, it during the period when the
requirement of energy is more than supply.
•A flywheel helps to keep the crankshaft rotating at
a uniform speed

In internal combustion engines,
• the energy is developed during one stroke and the
engine is to run for the whole cycle on the energy
produced during this one stroke.
• the energy is developed, only during power stroke
which is much more than the engine load; and no
energy is being developed during suction,
compression and exhaust strokes in case of 4 stroke
engines & during compression in case of 2 stroke
engines.
Flywheel

• The excess energy developed during
power stroke is absorbed by the flywheel and
releases it to the crankshaft during other strokes in
which no energy is developed, thus rotating the
crankshaft at a uniform speed.
• When the flywheel absorbs energy, its speed
increases and when it releases, the speed
decreases. Hence a flywheel does not maintain a
constant speed, it simply reduces the fluctuation of
speed.
Flywheel

• The function of a governor in engine is
entirely different from that of a flywheel
Governor regulates the mean speed of an engine
when there are variations in the load,
e.g., when the load on the engine increases it becomes
necessary to increase the supply of Working fluid. On the
other hand, when the load decreases, less working fluid is
required.
The governor automatically; controls the supply, of
working fluid to the engine with the varying load condition
and keeps the mean speed within certain limits.
Flywheel

• The flywheel does not maintain constant speed
• It simply reduces the fluctuation of speed.
• A flywheel controls the speed variations caused by
the fluctuation of the engine turning moment
during each cycle of operation.
It does not control the speed variations caused
by the varying load.
Flywheel

Capacity & Diameter
• The flywheel capacity of a given mass increases with its
distance from the axis of rotation ; consequently, if the
flywheel is made large in diameter it need not be so heavy.
• On the other hand there are two reasons for limiting the
diameter.
– At high rpm, flywheel is subjected to disruptive or bursting force,
& by keeping down the diameter, the F O S can be kept high.
– As it is cast or cast & pressed steel housing, this need not weigh so
much if the diameter is smaller
Flywheel

Flywheel
A Flywheel is given a high rotational inertia; i.e.,
most of its weight is well out from the axis

Construction of Flywheels
The flywheels of smaller size
(up to 600 mm diameter) are
casted in one piece.
The rim & hub are joined
together by means of web.
The holes in the web may
be made for handling purposes.

In case the flywheel is
of larger size (up to 2.5m
diameter), the arms are
made instead of web.
The number of arms
depends upon the size of
flywheel & its speed of
rotation.

The split flywheels are above 2.5m diameter & are
usually casted in two piece.
It has advantage of relieving shrinkage stresses in
arms due to unequal rate of cooling of casting.

Maximum Fluctuation of Speed
&
Coefficient of Fluctuation of Speed

•The Maximum Fluctuation of Speed
the difference between the maximum &
minimum speeds during a cycle. i.e., =(N1-N2)
Where, N1=Maximum speed in r.p.m. during the cycle,
N2=Minimum speed in r.p.m. during the cycle
•The Coefficient of Fluctuation of Speed is the ratio
of the maximum fluctuation of speed to the mean
speed.
Flywheel

 
 
   
 
   
 
 
   
 
 
1/Cs
m
Steadiness
of
t
Coefficien
flywheel.
of
design
the
in
factor
limiting
a
is
C
The
....
v
v
v
v
2
v
v
v
.....
ω
ω
ω
ω
2
ω
ω
ω
N
N
N
N
2
N
N
N
C
C
Speed
of
n
Fluctuatio
t
Coefficien
N
N
m
p
r
in
Speed
Mean
N
s
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
s
s
2
1
speeds
linear
of
terms
in
speeds
angular
of
terms
in
























 2
/
Flywheel

Fluctuation of Energy
The Fluctuation of Energy may be
determined by the turning moment
diagram for one complete cycle of
operation

• turning moment is
zero when the
crank angle is zero
• It rises to a max.
value when crank
angle reaches 90°
and it is again zero
when crank angle is
180°.
Flywheel

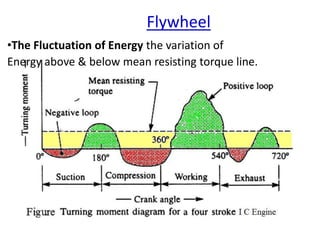
• work done=turning moment x angle turned
• The area of the turning moment diagram represents the
work done per revolution
• Engine is assumed to work against the mean resisting
torque,
• Since it is assumed that
work done by the turning moment / revolution =
work done against the mean resisting torque
Therefore,
area of rectangle (aAFe) is proportional to work done
against the mean resisting torque.
Flywheel

• When crank moves from 'a' to 'p'
work done by the engine is = area aBp,
whereas the energy required = area aABp.
• In other words, the engine has done less work than
the requirement. This amount of energy is taken
from the flywheel and hence the speed of the
flywheel decreases.
Flywheel

Now the
• crank moves from p to q,
• work done by the engine = area pBbCq
• requirement of energy = area pBCq
• Therefore the engine has done more work than the
requirement.
This excess work is stored in the flywheel and hence
the speed of the flywheel increases while the crank
moves from p to q.
Flywheel

• Similarly when the crank moves from q to r,
more work is taken from engine than is developed= area
CcD.
To supply this loss, the flywheel gives up some of its
energy and thus the speed decreases while the crank
moves from q to r.
• As the crank moves from r to s,
excess energy is again developed = area DdE
& the speed again increases.
• As the piston moves from s to e,
again there is a loss of work & the speed decreases.
Flywheel

•The variations of
energy above and
below the mean
resisting torque line
are called fluctuation
of energy.
The areas BbC,
CcD, DdE etc.
represent fluctuations
of energy.
Flywheel

• Engine has a max. speed either at q or at s.
This is due to the fact that flywheel absorbs energy
while the crank moves from p to q and from r to s.
• Engine has a minimum speed either at p or at r.
The reason is that flywheel gives out some of its energy
when the crank moves from a to p and q to r.
• The difference between the maximum and the minimum
energies is known as maximum fluctuation of energy.
Flywheel
Mean
Speed
Maximum Speed
Speed
Crankangle Min. Speed

Flywheel
•The Fluctuation of Energy the variation of
Energy above & below mean resisting torque line.

For a 4 Stroke IC Engine,
•During suction stroke, since the pr. inside the engine
cylinder is less than the atmospheric pr., a negative loop is
formed
•During compression stroke, the work is done on the
gases, there a higher negative loop is obtained
•In the working stroke, the fuel burns & the gases expand,
therefore a large positive loop is formed
•During exhaust stroke, the work is done on the gases,
therefore a negative loop is obtained
Flywheel

   
4
3
2
1
1 a
a
a
a
E
a
E
ΔE
Energy,
of
n
Fluctuatio
Maximum
ly.
respective
E
&
B
at
is
Energies
these
of
Min.
&
Max.
the
Let
A
at
Energy
a
a
a
a
a
a
E
G
at
Energy
a
a
a
a
a
E
F
at
Energy
a
a
a
a
E
E
at
Energy
a
a
a
E
D
at
Energy
a
a
E
C
at
Energy
a
E
B
at
Energy
fig.,
from
then
E,
A
at
flywheel
in
Energy
Let
6
5
4
3
2
1
5
4
3
2
1
4
3
2
1
3
2
1
2
1
1






































Coefficient of
Fluctuation of Energy

 
 
    ly
respective
Engines
C
I
st.
&
for
n
strokes/mi
working
of
No.
n
60
P
θ
rad/sec
in
ω
watts
in
P
θ
N
2π
60
P
cycle
per
done
Work
or
rad/sec
in
ω
watts
in
P
N
2π
60
P
m
-
N
in
torque
Mean
T
&
ly
respective
Engines
C
I
st.
&
for
&
rad/sec
in
turned
Angle
θ
where,
E
4
2
N/2
&
N
n
4
2
4π
2π
T
cycle
per
done
Work
Energy
Min.
-
Energy
Max.
cycle
per
done
Work
Energy
of
n
Fluctuatio
Max.
C
rpm
in
rpm
in
mean
mean
E
)
(C
energy
of
n
fluctuatio
of
t
Coefficien

























n
E
E
P 60


   



















 

























2
2
1
2
1
2
1
2
1
mk
I
&
)/ω/
ω
(ω
)/N
N
(N
s
)/2
ω
(ω
mean
)/2,
N
(N
mean
C
ω
N
where,
or
s
2
2
C
ω
I
ω
ω
ω
Iω
ω
I
2
1
ω
I
2
1
K.E
Min.
-
K.E
Max.
ΔE
ΔE
Energy,
of
n
fluctuatio
Max.
,
ω
to
ω
from
changes
speed
As
J
or
Nm
ω
mk
2
1
Iω
2
1
E
E
Flywheel
of
Energy
Kinetic
Mean
s
C
2E
ΔE
C
ω
mk
s
2
2
1
2
2
2
2
1
2
1
2
2
2
Flywheel
a
in
Stored
Energy

 
  out
found
be
can
t
&
b
,
2
usuallyb/t
ratio
b/t
Knowing
t,
b
A
then
r,
rectangula
be
to
rim
of
area
c/s
Assuming
density
vol.
m
rim
flywheel
of
Mass
determined
be
may
flywheel
of
mass
this
From
C
mv
C
ω
mR
ΔE
R
Rim
of
radius
mean
k
gyration
of
Radius
s
2
s
2
2
diameter,
to
compared
small
very
is
rim
of
thickness
As

























of rim
thickness
width & t
where,b
rim.
of
area
c/s
find
may
we
this
From
neglected
hub & arms
& that of
considered
of rim is
nertia
oment of i
nly mass m
ression, o
ve
in the abo
ρ
A
πR
R
v
2
,
exp
,



Example-1
The turning moment diagram for a
Petrol engine is drawn to following scales:
Turning moment, 1 mm =5 Nm; Crank angle, I mm = 1°;
The turning moment diagram repeats itself at every
half revolution of the engine and the areas above and below
mean turning moment line, taken in order are 295, 685, 40,
340, 960, 270 mm2.
Determine the mass of 300 mm diameter flywheel rim
when the coefficient of fluctuation of speed is 0.3% and the
engine runs at 1800 r.p.m..
Also determine the cross-section of the rim when the
width of the rim is twice of thickness. Assume density of rim
material as 7250 kg/m3.

Example-1…
•Solution;
Given:
ρ = 7250 kg/m3;
Cs = 0.3% = 0.003;
D = 300 mm or
R = 150 mm
= 0.15 m;
N =1800r.p.m. or
ω = 2 π x 1800 /60
= 188.5rad/s
m, b, t = ?
∆ E = Iω2Cs
= m.R2.ω2Cs
m = ρV
= ρ.(πD.A)
= ρ.(2πR.A)
A = b x t,
b=2t

•Mass of the flywheel (m kg)
As per given scale,
on the turning moment diagram,
1 mm2 = 5 Nm x 10 = 5 x(10 xπ /180) = 0.087 Nm
Max. fluctuation of energy = ∆ E = m.R2.ω2Cs
Let the total energy at A = E,
from fig., Energy at B = E + 295
Energy at C = E + 295 - 685 = E - 390
Energy at D = E - 390 + 40 = E - 350
Energy at E = E - 350 - 340 = E - 690
Energy at F = E - 690 + 960 = E + 270
Energy at G = E + 270 - 270 =E=Energy at A
Example-1…

:. Maximum energy =E+295 at B&
Minimum energy =E-690 at E
Maximum fluctuation of energy,
i.e. ∆ E =Max. energy – Min. energy
=(E + 295) - (E - 690) = 985 mm2
=985 x 0.087=86 Nm
Also, Maximum fluctuation of energy,
i.e. ∆ E = 86 =m.R2.ω2Cs
=m (0.15)2 (188.5)2 (0.003) = 2.4xm
:. m = 86/2.4 = 35.8 kg………Ans.
Example-1…

Example-1…
•Cross-section of the flywheel rim
Mass of the flywheel rim, m =Vol. x density
=(A x 2πR) xρ
Let, Width of rim, b=2 x t, thickness of rim
:. Cross-sectional area of rim, A=b x t = 2t x t = 2 t2
mass of the flywheel rim (m) = 35.8 = A x 2πRx ρ
=2 t2 X2 π x 0.15 x 7250
=13668 t2
:. t2 =35.8/13668 =0.0026
or t =0.051 m = 51mm….Ans.
& b =2 t =2 x 51 = 102 mm….Ans.

Example-2
A single cylinder, single acting,4
stroke oil engine develops 20 kW at
300 r.p.m.
The work done by the gases during expan.
stroke is 2.3 times the work done on the gases during
the compression and work done during the suction
and exhaust strokes is negligible.
The speed is to be maintained within ±1%.
Determine the mass moment of inertia of the
flywheel.

Solution; Given:
P = 20kW
=20x 103 W;
N = 300r.p.m. or
ω= 2πx300/60
=31.42rad/s
Cs=±1% or
ω1- ω2= ±1%ω
Example-2
∆ E = Iω2Cs

Example-2…
 
 
 
  






















Nm
/
/n
P
ycle
done per c
also, work
8000
150
60
10
20
60
3
Nm
8000
π
4
X
636.5
θ
X
T
ycle
workdone/c
Nm
636.5
300
2π
x60
10
20x
N
2
Px60
T
engine,
by
d
transmitte
torque
Mean
xCs
Ix
E
energy,
of
n
fluctuatio
Maximum
•
mean
3
mean
2
I
inertia,
of
moment
Mass



Example-2…
 
 
 
 
14160Nm
8000/0.565
W
0.565W
/2.3
W
W
8000Nm
or
W
W
cycle
per
workdone
done
work
Net
stroke
expn.
during
done
work
W
&
stroke
comprn.
during
done
work
W
let,
E
E
E
E
C
E
E
C













The work done during expan. stroke
is shown by triangle ABC in Fig., in which
base AC =π radians & height BF =Tmax
:. Work done during expansion stroke,
WE =14160 =(1/2) X π X Tmax = 1.571 Tmax
Or Tmax= 14160/1.571 = 9013 Nm
Height above the mean torque line,
BG = BF - FG = Tmax- Tmean
= 9013 - 636.5 = 8376.5 Nm
Example-2…

Example-2…
 
   
 
 
 
 
 
 
    N-m
.
x
.
x
/
x DE x BG
/
BDE)
le
a ofΔ
(i.e., are
:. Δ.
rad
.
π
.
π
T
)
mean
-T
(T
AC
BF
BG
DE
or
BF
BG
AC
DE
and BAC,
ngles BDE
milar tria
s, From si
as follow
calculated
ΔE may be
also,
12230
5
8376
92
2
2
1
2
1
92
2
9013
5
8376
max
max






















Nm
12230
9013
8376.5
14160
T
)
T
-
(T
W
E
Δ
BF
(BG)
W
BF
(BG)
ABC
Δ
of
Area
E
i.e.Δ
BDE),
Δ
of
Area
(i.e.
energy
of
n
fluctuatio
Max.
,
BF
(BG)
ABC
Δ
of
Area
BDE
Δ
of
Area
relation,
l
geometrica
from
2
2
2
max
2
mean
max
E
2
2
E
2
2
le
le
2
2
le
le

Example-2…
  .Ans
..........
619.5kgm
4
12230/19.7
I 2
I
19.74
0.02
(31.42)
I
C
Iω
12230
i.e.
C
Iω
ΔE
E
energy,
of
n
fluctuatio
maximum
that
know
We
.
kgm
in
flywheel
the
of
inertia
of
moment
Mass
I
Let
0.02
ω
ω
-
ω
C
speed,
of
n
fluctuatio
of
t
coefficien
and
ω
0.02
ω
%
2
ω
-
ω
speed
of
n
fluctuatio
total
therefore
speed,
mean
the
of
1%
within
maintained
be
to
is
speed
the
Since
2
s
2
s
2
2
2
1
s
2
1
















Stresses in a Flywheel Rim
•A flywheel, consists of a rim at which major
portion of mass or weight is concentrated.
•Following types of stresses are induced in the rim
1. Tensile stress due to centrifugal force,
2. Tensile bending stress caused by the restraint
of the arms, and
3. The shrinkage stresses due to unequal rate of
cooling of casting. This stress is taken care of by
a factor of safety.
b = Width of rim,
t =Thickness of rim,
A = Cross-sectional area
of rim = b x t.
D = Mean diameter of
flywheel
R =Mean radius of
flywheel,
ρ =Density of flywheel
material,
ω =Angular speed of
flywheel,
V =Linear velocity of
flywheel, and
σt =Tensile/hoop stress

Stresses in Rim
1. Tensile stress due to centrifugal force
The tensile stress in the rim due
to the centrifugal force, assuming
that rim is unstrained by arms, is
determined in a similar way as a
thin cylinder subjected to internal pr..
Tensile stress,
σt =ρ.R2.ω2 =ρ.v2 ...(v = ω.R)
(when ρ is in kg/m3 and v is in m/s, then σt will be in N/m2 or Pa)
Note: From the above expression the mean diameter (D) of the
flywheel may be obtained by using the relation v=πDN / 60

 
   
t
n
R
ρv
.
b
σ
v /R)
ing
(Substitut
t
n
R
ρω
.
bt
n
πR
R
btρ
bt
wl
Z
M
σb
























2
2
74
19
6
2
12
6
12
74
19
2
3
2
2
2
2
2
2


b
σ
stress,
Bending
loaded,
uniformly
and
ends
both
at
fixed
beam
a
like
behaves
arms
of
pair
a
betn.
rim
of
portion
each
that
assumption
the
on
based
is
arms
of
restraint
the
to
due
rim
the
in
stress
bending
tensile
The
arms
the
of
restraint
by
caused
stress
bending
Tensile
2.
Stresses in Rim





































t
n
R
ρv
b
t
b
t
t
n
R
ρv
.
ρv
b
t
2
2 935
.
4
75
.
0
4
1
4
3
,
2
2
74
19
4
1
2
4
3








,
T
expansion.
free
for
necessary
amount
the
of
4
3
about
stretch
flywheel
a
of
arms
The
zero.
be
will
i.e.,
arms,
the
to
due
restraint
no
be
will
there
action,
l
centrifuga
to
due
rim
the
of
expansion
free
allow
to
enough
stretched
are
arms
if
hand
other
the
On
zero
be
will
i.e.,
rim,
in
stress
up
set
not
will
force
l
centrifuga
then
together,
close
very
placed
are
&
stretch
not
do
arms
If
rim
the
in
stress
otal
rim,
the
in
stress
total
Now
th
Stresses in Rim

Example-3
A multi-cylinder engine is to run at a
constant load at a speed of 600 r.p.m.
On drawing the crank effort diagram
to scale of 1 m = 250 Nm and 1 mm = 3°,
The areas in mm2 above & below mean torque line are:
+ 160,- 172, + 168,- 191, + 197,- 162 mm2
The speed is to be kept within ±1% of the mean
speed of the engine. Calculate the necessary moment of
inertia of the flywheel.
Determine suitable dimensions for cast iron
flywheel with a rim whose breadth is twice its radial
thickness. The density of cast iron is 7250 kg/m3, and its
working stress in tension is 6MPa.
Assume that rim contributes 92% of flywheel effect.

Example-3
•Solution. Given:
N =600 r.p.m. or
ω =2π x 600/60 =62.84 rad/s;
ρ =7250 kg/m3; σt =6 MPa =6 x 106 N/m2
∆ E = Iω2Cs
σt=ρ.v2
v = (πDN)/60
∆ E = m.R2.ω2Cs
m = ρV = ρ.(πD.A)= ρ.(2πR.A)
A = b x t,
b=2t

•Moment of inertia of the flywheel
We know that,
Maximum fluctuation of energy, ∆E= Ixω2xCs
Scale for the turning moment is
1 mm = 250 Nm & scale for the crank angle is
1 mm = 3°= 3°xπ/180= π/60 rad, therefore
1 mm2 on the turning moment diagram
i.e., 1 mm2 =250 x π/60 = 13.1 Nm
Example-3

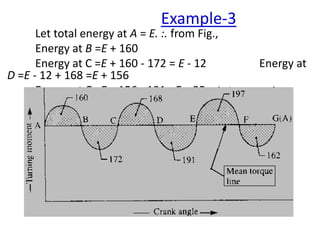
Let total energy at A = E. :. from Fig.,
Energy at B =E + 160
Energy at C =E + 160 - 172 = E - 12 Energy at
D =E - 12 + 168 =E + 156
Energy at E =E + 156 - 191 =E – 35 (min. energy)
Energy at F = E - 35 + 197 =E + 162 (max. energy)
Energy at G =E + 162 - 162 = E =Energy at A
Max. fluctuation of energy,
∆ E =Max. energy – Min. energy
= (E + 162) - (E - 35)
= 197 mm2
∆ E =197 x 13.1=2581 N-m
Example-3

Since the fluctuation of speed is±1%
of the mean speed (ω),
therefore total fluctuation of speed,
ω1-ω2= 2% ω = 0.02ω
& coefficient of fluctuation of speed,
Cs =[(ω1-ω2)/ω] = 0.02
maximum fluctuation of energy, ∆E,
∆E, = 2581 = I.ω2.Cs = I (62.84)2 0.02 = 79xI
:. I = 2581/79 = 32.7 kgm2…..Ans
Example-3

•Dimensions of a flywheel rim
We know that, Mass of the flywheel rim,
m = Vol. x density =2πR x A x ρ = πD x (b x t )x ρ b=2t (given)
•Peripheral velocity (v) & mean diameter (D)
We know that, tensile stress, σt=ρ.v2
i.e., σt=6 x 106=ρ.v2 =7250 X v2
So, v2 =(6 x 106)/7250 =827.6 or v =28.76 m/s
We also know that, peripheral velocity,v = (πDN)/60
i.e., v=28.76 = (πDN)/60 = (πDx600)/60 = 31.42 D
So D = 28.76/31.42 = 0.915 m = 915 mm …Ans.
Example-3

•Mass of flywheel rim
Since rim contributes 92% of flywheel effect,
:. Energy of flywheel rim, Erim = 0.92 x total Energy of
the flywheel, E
Max. fluctuation of energy, ∆E= E x 2 Cs
i.e., ∆E =2581 = E x 2 Cs =E x 2 x 0.02 = 0.04 E
:. E = 2581/ 0.04 = 64525 N-m
& Energy of flywheel rim, Erim = 0.92 E
(v=ωR) = 0.92 x 64525 = 59363 Nm
Also, Erim= (1/2)Iω2 = (1/2)mk2ω2 = (1/2)mR2ω2 = (1/2)xmxv2
i.e., 59363 = 1/2 x m x v2 = 1/2 x m (28.76)2 = 413.6 m
:. m = 59363/413.6 = 143.5 kg
Example-3

The mass of the flywheel rim may also
be obtained by using following relations.
Since the rim contributes 92% of the flywheel effect,
•Irim = 0.92xIflywheel or m.k2= 0.92 x 32.7 =30 kgm2
Since radius of gyration, k =R =D/2 = 0.915/2 =0.4575m,
i.e., m=(30/k2) =(30/0.45752) =(30/0.2092)=143.5kg
•(∆ E) rim = 0.92 (∆ E )flywheel
m. V2.CS = 0.92 (∆ E )flywheel
m (28.76)2x0.02= 0.92x 2581
16,55xm = 2374.5
or m = 2374.5/16.55= 143.5kg
Example-3

m = 59363/413.6 = 143.5 kg
Also,mass of the flywheel rim,
m= (b x t )x πD x ρ & b=2t (given)
143.5 = b x t x πD x ρ
=2 t X t X π x 0.915 x 7250 = 41686 t2
t2 = 143.5/41686 =0.00344
t =0.0587 say 0.06 m =60 mm Ans.
b =2 t =2 x 60 = 120 mm Ans.
Example-3

Example-4
An otto cycle engine develops 50 kW at
150 r.p.m. with 75 explosions per minute.
The change of speed from the commencement to the
end of power stroke must not exceed 0.5% of mean on either
side.
Design a suitable rim section having width four times
the depth so that the hoop stress does not exceed 4 MPa.
Assume that the flywheel stores 16/15 times the
energy stored by the rim and that the workdone during
power stroke is 1.40 times the workdone during the cycle.
Density of rim material is 7200 kg/m3

•Solution.
Given:
P =50 kW
=50 X 103W;
N = 150r.p.m.;
n =75 ;
σt =4 MPa
=4 x 106 N/m2;
ρ =7200 kg/m3
Example-4

We know that, Mass of the flywheel rim,
m =Vol. x density=2πR x A x ρ
i.e., m=(b x t )x πD x ρ & [b=4t (given)]
Further, Energy of the flywheel rim,
Erim= (1/2)Iω2 = (1/2)mk2ω2 = (1/2)mR2ω2 (v=ωR)
= (1/2)xmxv2 [Erim=(15/16)E …given]
And Max. fluctuation of energy, ∆E= E x 2 Cs
& hoop Stress=σt=ρv2 & v=πDN/60
Example-4

Tmean transmitted by the engine or flywheel.
Power transmitted, P= (2xπxNxTmean)/60
i.e., 50x103= (2xπx150xTmean)/60 =15.71 Tmean
Tmean= 50 x 103/15.71= 3182.7 N-m
Workdone/cycle = Tmeanx θ = 3182.7 x 4 π= 40000 Nm
{Or The workdone per cycle for a 4 stroke engine,
Workdone l cycle =[(Px60)/(No. of explosions/min)]
=(Px60)/n = (50000x60)/75=40000 Nm}
:. Workdone during power stroke =1.4xWorkdone/cycle
=1.4x40000 = 56000 N-m
Example-4

The workdone during power stroke is shown
by ∆le ABC in Fig
in which base AC =π radians and height BF = Tmax
:. Workdone during working stroke= 1/2xπXTmax
= 1.571 Tmax
:. Also Workdone during working stroke=56000 Nm
:. Tmax=(56000/1.571) =35646Nm
Height above the mean torque line,
BG = BF-FG = Tmax-Tmean
= 35646-3182.7= 32463.3Nm
Example-4

Example-4
Nm
46480
E 0.83
x
000
56
35646
32463.3
x
56000
)
(BF
(BG)
x
ABC
triangle
of
Area
E
BDE
of
Area
BDE),
triangle
of
area
(i.e.,
energy
of
n
fluctuatio
Maximum
)
(BF
(BG)
ABC
of
Area
BDE
of
Area
relation
l
geometrica
from
E),
(
energy
of
n
fluctuatio
max.
represents
line
torque
mean
the
above
Fig)
in
shaded
(shown
BDE
area
the
Since
2
2
2
le
2
2
le
le




















Mean diameter of the flywheel (D)
Hoop stress, σt=ρv2
i.e., 4 x 106= ρ.v2 = 7200 X v2
:. v2 =4 X 106/7200 = 556
or v = 23.58 m/s
Peripheral velocity, v = πDN/60
i.e., 23.58 = πDN/60 = πDx150/60 =7.855 D
D =23.58/7.855
D=3 m …Ans.
Example-4

Cross-sectional dimensions of the rim
Cross-sectional area of the rim,
A=b x t= 4t x t =4t2 (b=4t..given)
Since N1 - N2 = 0.5% N either side, (..given)
:. total fluctuation of speed,
N1 - N2 = 1% of mean speed =0.01 N
& coefficient of fluctuation of speed,
Cs. = (N1 - N2)/N = 0.01
E = Total energy of the flywheel.
Maximum fluctuation of energy (∆ E),
46480 = Ex 2 Cs = E x 2 x 0.01 = 0.02 E
:. E = 46480/0.02 =2324 x 103 Nm
Example-4

Since the energy stored by the flywheel is
16/15 times the energy stored by rim,
Therefore the energy of the rim,
Erim = (16/15)E= (16/15)x 2324 x 103 = 2178.8 x 103Nm
Also Erim= (1/2)xmxv2
i.e., 2178.8 X 103 = (1/2)xmx(23.58)2 =278xm
:. m = 2178.8 x103 / 278 =7837 kg
Also, mass of the flywheel rim, m= A x πD x ρ
i.e., 7837 = A x πD x ρ =4 t 2 X π X 3 x 7200 =271469 t2
or t2 = 7837 / 271469 = 0.0288
or t = 0.17 m = 170 mm …Ans.
b =4 t =4 x 170 = 680 mm …Ans.
Example-4

Example-5
.
7200kg/m
as
taken
be
may
iron
cast
of
Density
.
39.23N/mm
as
taken
be
may
key
and
shaft
for
stress
shear
Safe
The
torque.
mean
the
twice
is
shaft
the
on
torque
maximum
The
cycle.
whole
the
during
done
work
average
the
times
3
1
1
is
stroke
power
the
during
done
work
the
that
assumed
be
may
It
speed.
mean
of
4%
to
limited
be
to
is
speed
of
n
fluctuatio
total
The
.
3.92N/mm
exceed
to
not
is
material
the
in
stress
hoop
The
800rpm.
at
36.8kW
Developing
Engine
Diesel
stroke
4
a
for
Flywheel
iron
cast
a
Design
3
2
2

Example-5…
3
2
s
mean
max
s
2
7200kg/m
iron
cast
of
Density
39.23N/mm
f
stress
shear
Safe
T
T
cycle
whole
the
during
done
work
ave.
3
1
1
stroke
power
during
done
Work
0.04
K
speed
of
n
Fluctuatio
3.92N/mm
material
in
stress
Hoop
800rpm
@
36.8kw
Power
Flywheel
iron
Cast
Given,
:
Solution










∆ E = Iω2Cs
σt=ρ.v2
v = (πDN)/60
∆ E = m.R2.ω2Cs
m = ρV = ρ.(πD.A)= ρ.(2πR.A)
A = b x t,
b=2t

Example-5…
 
 
50mm
is
diameter
shaft
,
d
i.e.,
50mm
49mm
0.049m
d
10
39.23
π
16
878.54
d
f
16
d
π
878.54Nm
439.27
2
T
2
T
But
439.27Nm
800
π
2
60000
36.8
N
π
2
60000
Power
T
kW
60000
T
N
π
2
Power
that,
know
We
s
s
6
3
s
s
3
s
mean
max
mean
mean
book
hand
data
in
eqn.3.1
ref.,
































 
5980Nm
4
5520
7360
Energy
Min.
Energy
Max.
energy
of
n
Fluctuatio
7360Nm
3
1
1
5520
done/cycle
Work
3
1
1
stroke
power
during
done
Work
5520Nm
4π
439.27
720
439.27
turned θ
Angle
momentT
Turning
done/cycle
Work
100mm
50
2
d
2
diameter
hub
or
diameter
Boss
0
mean
s
book
hand
data
in
eqn.17.8
ref.,























E
Example-5…

Example-5…
 
 
546mm
D
rim
of
dia.
Mean
i.e.,
0.5460m
D
or
1.02N
D
π
23.33
V
,
N
D
π
V
Also
23.33m/s
V
or
V
7200
10
3.92
,
V
ρ
σ
stress
Hoop
As
ec
21.30N.m.s
I
N
π
2
0.04
I
5980
E
ω
C
I
E
Also,
1.02N)
max
N
speed,
mean
of
4%
to
limited
speed
of
n
fluctuatio
total
(
rim
of
velocity
V
&
density
ρ
speed
of
n
fluctuatio
of
t
coefficien
s
C
&
speed
angular
Mean
ω
max
2
6
2
max
2
2
,
2
s


































60
60
60


Example-5…
 
   
  0.0761m
t
t
4t
0.546
π
0.0397
4t
b
let,
,
t
b
πD
Area
R
2
V
Also,
0.0397m
9.81
7200
2803
g
ρ
2803
w
,
W
,
V
further,
2803N
W
Weight,
2
0.546
9.81
W
2
D
g
W
21.3
I
wheel}
rimmed
thin
for
R
rim,
of
radius
mean
{k
mk
gyration
of
radius
flywheel
of
mass
rotation
of
axis
about
inertia
of
momemt
mass
I
that,
know
We
rim
3
rim
2
2
2
2
density
Weight












































.,
.e
i

Example-5…
469.9mm
622.1mm
304.4mm
76.1
4
4t
b
76.1mm,
t
0.4699m
0.0761
0.546
t
D
flywheel
the
of
diameter
Inside
0.6221m
0.0761
0.546
t
D
flywheel
the
of
diameter
Outside
or
mean
mean



















Stresses in Flywheel Arms
Following stresses are induced
in the arms of a flywheel
•Tensile stress due to centrifugal force acting on the
rim.
•Bending stress due to torque transmitted from the
rim to the shaft or from the shaft to the rim.
•Shrinkage stresses due to unequal rate of cooling of
casting. These stresses are difficult to determine.

•Tensile stress due to centrifugal force
Due to the centrifugal force acting on the
rim, the arms will be subjected to direct tensile stress
whose magnitude is,
:. Tensile stress in the arms,
σt1= (3/4)σt= (3/4)ρxv2

•Bending stress due to torque transmitted
T =Maximum torque transmitted by the shaft,
Z = Section modulus for the c/s of arms &
R =Mean radius of rim
r =Radius of the hub
n =Number of arms

1
1 b
t 















end,
hub
the
at
arms
the
in
stress
tensile
Total
r)
-
(R
Z
n
R
T
Z
M
arms,
in
stress
Bending
r)
-
(R
n
R
T
M
i.e.,
hub,
the
at
arm
the
on
lies
which
moment
bending
max.
&
n
R
T
arm
each
on
Load
R
T
F
rim,
the
of
radius
mean
the
at
Load
b1
Stresses in Arms

D/n of Arms
   
 
(2)
&
(1)
equations
by
obtained
dimensions
arms
,
b
2
a
Assuming
2
r).......
-
(R
Z
n
R
T
Z
M
σ
arms,
in
stress
ding
MaximumBen
r)
-
(R
n
R
T
M
moment,
bending
maximum
that
know
We
1
.......
a
b
x
32
π
Z
modulus,
Section
stress.
bending
max.
for
desgnedned
is
it
&
axis,
minor
the
twice
as
axis
major
with
elliptical
usually
is
arms
the
of
c/s
The
1
1
b
2
1
1










Design of Shaft, Hub and Key
 
shaft.
of
material
the
for
stress
shear
Allowable
&
shaft,
the
of
Diameter
d
where,
16
T
d,
transmitte
torque
Maximum
d.
transmitte
torque
maximum
the
from
obtained
is
flywheel
for
shaft
of
diameter
The
1
max







 3
1
d

therim.
of
width
to
equal
taken
generally
is
It
diameter.
shaft
the
times
2.5
to
2
from
length
Hub
&
dia.
shaft
the
twice
as
taken
usually
is
diameter
Hub
shaft.
of
diameter
or
hub
of
diameter
Inner
d
&
hub,
of
diameter
Outer
d
where,
16
T
d,
transmitte
torque
Max.
d.
transmitte
torque
maximum
the
for
shaft,
hollow
a
as
designed
is
hub
The
1
max









 



d
d
d
4
1
4


Shaft, Hub and Key

shaft.
of
Diameter
d
al
key.materi
the
for
stress
Shear
key,
the
of
Length
L
where,
2
d
x
Lx w x
Tmax
shaft,
by
d
transmitte
Torque
shearing.
in
key
of
failure
the
g
considerin
by
obtained
is
key
of
length
The
hub.
&
shaft
the
for
used
is
key
sunk
standard
A
1
1




&


Design of Shaft, Hub and Key

Design and draw a cast iron flywheel
used for a four stroke I.C engine
developing180 kW at 240 r.p.m.
The hoop or centrifugal stress developed in the
flywheel is5.2 MPa, the total fluctuation of speed is
to be limited to 3% of the mean speed. The work
done during the power stroke is 1/3 more than the
average work done during the whole cycle.
The max. torque on shaft is twice the mean
torque. The density of cast iron is 7220 kg/m3.
Example-6

Solution.
Given:
P =180kW
=180X 103W;
N = 240r.p.m.;
σt = 5.2MPa
= 5.2x 106N/m2;
Nl - N2 = 3% N;
ρ = 7220 kg/m3
.
Turning moment diagram of a 4
stroke engine is shown in Fig.
Example-6

Nm
x
x
cycle
done
Work
:.
N
ine, n
stroke eng
For
g strokes
of workin
No
where n
,
n
P
cycle
Workdone
tained as
also be ob
cycle may
workdone
90000
120
60
10
180
/
2
/
4
.
min
/
.
60
/
,
/
3
40















Nm
90000
4
x
7161
x
T
ycle
workdone/c
Nm
7161
2
2
60
x
10
180x
N
2
60
Px
T
flywheel,
the
by
d
transmitte
torque
Mean
E)
(
energy
of
n
fluctuatio
Maximum
mean
3
mean




Example-6

Example-6
 
  Nm
76384
2
120000x
T
120000
T
X
x
T
X
x
stroke
power
during
Workdone
T
BF
height
&
radians
AC
base
which,
in
Fig.
in
ABC
a
by
shown
is
stroke
power
the
during
Workdone
Nm
120000
90000
x
3
1
90000
stroke
working)
(or
power
the
during
Workdone
cycle,
whole
during
workdone
average
than
more
times
1/3
is
stroke
power
during
workdone
Since
max
max
max
max
le
















2
1
2
1

Example-6
Nm
98555
(76384)
(69223)
120000
(BF)
(BG)
x
ABC
Δ
of
Area
BDE
Δ
of
Area
E
energy,
of
n
fluctuatio
Max.
,
(BF)
(BG)
:
ABC
Δ
of
Area
BDE
Δ
of
Area
relation,
l
geometrica
from
E),
(
energy
nof
fluctuatio
max.
the
represents
line
torque
mean
the
above
Fig.
in
shaded
shown
BDE
area
the
Since
Nm
69223
7161
-
76384
T
-
T
FG
-
BF
BG
line,
torque
mean
the
above
Height
2
2
2
2
le
le
2
2
le
le
mean
max















Example-6
Ans.
...
m
2.04
26.8/13.1
D
rim
flywheel
the
of
Diameter
1.
D
13.1
60
250
D
N
D
26.8
v
velocity,
Peripheral
or
720
/7220
10
X
5.2
V
V
X
7220
.V
10
x
5.2
rim,
flywheel
the
in
developed
stress
Hoop
m/s
26.8
v
6
2
2
2
6
t





















60

Example-6
 
.....Ans.
kg
4995
555/19.73
98
m
rim
flywheel
the
of
Mass
2.
19.73m
0.03
(25.14)
2
2.04
m
98555
E
C
,
.
m.R
98555
E
energy,
of
n
fluctuatio
Max.
0.03
N
N
-
N
Cs
speed,
of
n
fluctuatio
of
t
Coefficien
&
rad/s
25.14
60
x250
2
60
xN
2
rim,
flywheel
the
of
speed
Angular
2
2
s
2
2
2
1




















Example-6
Ans
mm...
470
235
2
t
2
b
......Ans.
mm
235
t
or
rim
of
dimensions
sectional
-
Cross
3.
&
m
0.235
say
0.232
t
or
0.054
4995/92556
t
t
92556
7220
x
2.04
t
2
m
x
D
A x
4995
m
rim,
flywheel
the
Massof
t
2
t
t
2
t
b
A
rim,
the
of
area
sectional
-
Cross
t(Assume)
2
metres
in
rim
the
of
Width
b
&
metres,
in
rim
of
thickness
or
Depth
t
Let
2
2
2
2





























Example-6
Ans
mm........
0.47
mm
470
b
I
&
m
0.25
mm
250
125
x
2
d
2
d
.
.......Ans
125mm
say
122
d
hub
of
length
and
Diameter
4.
1
1
or
)
(d
7.855
)
(d
)
(d
10
x
14322
T
shaft,
the
on
acting
torque
maximum
Also,
mm
-
N
10
x
14322
Nm
14322
7161
x
2
T
x
2
T
shaft,
the
on
acting
torque
Max.
T
x
2
T
Since
hub,
of
Length
l
&
d
hub,
of
Diameter
d
shaft,
of
Diameter
d
Let
)
2
N/mm
40
MPa
40
(Taking
3
1
3
1
3
1
3
max
3
mean
max
mean
max
1



























,
40
16
16
,
that
know
We





Example-6
Nmm
10
x
2094.5
Nm
2094.5
Nm
0.25)
-
(2.04
6
2.04
14322
d)
-
(D
n
D
T
r)
-
(R
n
R
T
M
by,
given
is
cantilever
as
assumed
is
which
end,
hub
the
at
arm
in
moment
bending
max.
)
...(Assume
N/mm
15
MPa
15
arms
of
material
for
stress
Bending
)
...(Assume
a
0.5
axis
Minor
b
axis,
Major
a
)
...(Assume
6
arms
of
Number
n
Let
3
2
b
1
1
1
arms
elliptical
of
dimensions
sectional
Cross
5.


















Example-6
....Ans
mm
70
140
x
0.5
1
a
0.5
1
b
....Ans.
mm
140
1
a
arms.....
elliptical
of
dimensions
sectional
Cross
or
10
x
2793
/15
10
x
890
41
)
(a
)
(a
10
890
41
)
(a
0.05
10
2094.5x
Z
M
15
,
stress
bending
the
that
know
We
)
(a
0.05
)
(a
0.5a
)
(a
b
Z
arm.
the
of
section
-
cross
the
for
modulus
section
The
3
3
3
1
3
1
3
3
1
3
b
3
1
2
1
1
2
1
1

















&
32
32




Example-6
    ....Ans.
mm
160
say
159
L
......Ans
mm
20
key
of
thickness
&
s
........An
mm
36
w
key
of
Width
key
of
Dimensions
6.
3
3
3
3
max
10
90
/
10
x
14322
L
10
90
2
125
x
40
x
36
x
L
d
w
L
10
x
14322
T
,
shaft
the
by
d
transmitte
torque
Max.
.
:
follows
as
are
mm
125
diameter
of
shaft
a
for
key
sunk
r
rectangula
of
dimensions
standard
The
shearing
in
key
of
failure
g
considerin
by
obtd.
is
(L)
key
of
Length














2
1


 
 
safe.
is
design
MPa,
15
than
less
is
Since
MPa.
15
than
greater
be
not
should
which
rim
in
stress
total
for
Check
MPa
6.97
N/m
10
x
6.97
0.595)
(0.75
10
x
5.18
N/m
0.235
6
2
2.04
4.935
0.75
26.8
7220
t
n
R
4.935
0.75
ρv
σ
rim,
the
in
stress
total
that,
know
We
2
6
6
2
2
2
2
2































Example-6

DEsign of Flywheel new.ppt

More Related Content

What's hot (20)

Similar to DEsign of Flywheel new.ppt (20)

More from dharma raja` (20)

Recently uploaded (20)

DEsign of Flywheel new.ppt